title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
[Python] Top down spaghetti solution - Authentic like Italian cuisine | paint-house-iii | 0 | 1 | # Intuition\nWe first need to understand the idea of having neighborhoods. It the most basic sense, it\'s the number of color switch between different neighbors plus 1.\n\nFor example, `houses = [1, 2, 2, 1, 1]`, number of `color` switchs are `2`, and we have `3` neighborhoods.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nSimilar to other paint house problem, with a few conditions to check for the `houses` that had already been painted. Also we need to introduce a new variable `group` to count the number of time that we have different `colors` between neighbor.\n\n\n\n# Code\n```\nclass Solution:\n def minCost(self, houses: List[int], cost: List[List[int]], m: int, n: int, target: int) -> int:\n\n @cache\n def dp(i, j, group):\n if i == len(cost) and group == target: return 0\n if i >= len(cost): return float("inf")\n if group > target: return float("inf")\n\n res = float("inf")\n if not houses[i]:\n for color in range(1, n + 1):\n if j != color:\n res = min(res, dp(i + 1, color, group + 1) + cost[i][color - 1])\n else:\n res = min(res, dp(i + 1, color, group) + cost[i][color - 1])\n else:\n color = houses[i]\n res = dp(i + 1, color, group + 1) if j != color else dp(i + 1, color, group)\n\n return res\n\n res = dp(0, -1, 0)\n return -1 if res == float("inf") else res\n``` | 1 | You are given a list of `preferences` for `n` friends, where `n` is always **even**.
For each person `i`, `preferences[i]` contains a list of friends **sorted** in the **order of preference**. In other words, a friend earlier in the list is more preferred than a friend later in the list. Friends in each list are denoted by integers from `0` to `n-1`.
All the friends are divided into pairs. The pairings are given in a list `pairs`, where `pairs[i] = [xi, yi]` denotes `xi` is paired with `yi` and `yi` is paired with `xi`.
However, this pairing may cause some of the friends to be unhappy. A friend `x` is unhappy if `x` is paired with `y` and there exists a friend `u` who is paired with `v` but:
* `x` prefers `u` over `y`, and
* `u` prefers `x` over `v`.
Return _the number of unhappy friends_.
**Example 1:**
**Input:** n = 4, preferences = \[\[1, 2, 3\], \[3, 2, 0\], \[3, 1, 0\], \[1, 2, 0\]\], pairs = \[\[0, 1\], \[2, 3\]\]
**Output:** 2
**Explanation:**
Friend 1 is unhappy because:
- 1 is paired with 0 but prefers 3 over 0, and
- 3 prefers 1 over 2.
Friend 3 is unhappy because:
- 3 is paired with 2 but prefers 1 over 2, and
- 1 prefers 3 over 0.
Friends 0 and 2 are happy.
**Example 2:**
**Input:** n = 2, preferences = \[\[1\], \[0\]\], pairs = \[\[1, 0\]\]
**Output:** 0
**Explanation:** Both friends 0 and 1 are happy.
**Example 3:**
**Input:** n = 4, preferences = \[\[1, 3, 2\], \[2, 3, 0\], \[1, 3, 0\], \[0, 2, 1\]\], pairs = \[\[1, 3\], \[0, 2\]\]
**Output:** 4
**Constraints:**
* `2 <= n <= 500`
* `n` is even.
* `preferences.length == n`
* `preferences[i].length == n - 1`
* `0 <= preferences[i][j] <= n - 1`
* `preferences[i]` does not contain `i`.
* All values in `preferences[i]` are unique.
* `pairs.length == n/2`
* `pairs[i].length == 2`
* `xi != yi`
* `0 <= xi, yi <= n - 1`
* Each person is contained in **exactly one** pair. | Use Dynamic programming. Define dp[i][j][k] as the minimum cost where we have k neighborhoods in the first i houses and the i-th house is painted with the color j. |
Python3 | Space Optimized | paint-house-iii | 0 | 1 | # Approach\n* Code is self-explanatory\n\n# Complexity\n- Time complexity: $$O(M \\cdot T \\cdot N^2)$$\n\n- Space complexity: $$O(T \\cdot N)$$\n\n# Code\n```\nclass Solution:\n def minCost(self, houses: List[int], cost: List[List[int]], m: int, n: int, target: int) -> int:\n dp = [[+inf for _ in range(n)] for _ in range(target+1)]\n # [number_of_neighbourhoods][last_color] = min_cost\n for color in range(n):\n dp[0][color] = 0\n for i in range(m):\n new_dp = [[+inf for _ in range(n)] for _ in range(m+1)]\n for prev_neighbourhoods in range(target+1):\n for prev_color in range(n):\n if houses[i]-1 == -1:\n for color in range(n):\n neighbourhoods = max(1, prev_neighbourhoods + (prev_color != color))\n if neighbourhoods > target: continue\n new_dp[neighbourhoods][color] = min(\n new_dp[neighbourhoods][color],\n dp[prev_neighbourhoods][prev_color] + cost[i][color],\n )\n else:\n color = houses[i]-1\n neighbourhoods = max(1, prev_neighbourhoods + (prev_color != color))\n if neighbourhoods > target: continue\n new_dp[neighbourhoods][color] = min(\n new_dp[neighbourhoods][color],\n dp[prev_neighbourhoods][prev_color],\n )\n dp = new_dp\n ans = min(dp[target])\n return ans if ans != +inf else -1\n``` | 1 | There is a row of `m` houses in a small city, each house must be painted with one of the `n` colors (labeled from `1` to `n`), some houses that have been painted last summer should not be painted again.
A neighborhood is a maximal group of continuous houses that are painted with the same color.
* For example: `houses = [1,2,2,3,3,2,1,1]` contains `5` neighborhoods `[{1}, {2,2}, {3,3}, {2}, {1,1}]`.
Given an array `houses`, an `m x n` matrix `cost` and an integer `target` where:
* `houses[i]`: is the color of the house `i`, and `0` if the house is not painted yet.
* `cost[i][j]`: is the cost of paint the house `i` with the color `j + 1`.
Return _the minimum cost of painting all the remaining houses in such a way that there are exactly_ `target` _neighborhoods_. If it is not possible, return `-1`.
**Example 1:**
**Input:** houses = \[0,0,0,0,0\], cost = \[\[1,10\],\[10,1\],\[10,1\],\[1,10\],\[5,1\]\], m = 5, n = 2, target = 3
**Output:** 9
**Explanation:** Paint houses of this way \[1,2,2,1,1\]
This array contains target = 3 neighborhoods, \[{1}, {2,2}, {1,1}\].
Cost of paint all houses (1 + 1 + 1 + 1 + 5) = 9.
**Example 2:**
**Input:** houses = \[0,2,1,2,0\], cost = \[\[1,10\],\[10,1\],\[10,1\],\[1,10\],\[5,1\]\], m = 5, n = 2, target = 3
**Output:** 11
**Explanation:** Some houses are already painted, Paint the houses of this way \[2,2,1,2,2\]
This array contains target = 3 neighborhoods, \[{2,2}, {1}, {2,2}\].
Cost of paint the first and last house (10 + 1) = 11.
**Example 3:**
**Input:** houses = \[3,1,2,3\], cost = \[\[1,1,1\],\[1,1,1\],\[1,1,1\],\[1,1,1\]\], m = 4, n = 3, target = 3
**Output:** -1
**Explanation:** Houses are already painted with a total of 4 neighborhoods \[{3},{1},{2},{3}\] different of target = 3.
**Constraints:**
* `m == houses.length == cost.length`
* `n == cost[i].length`
* `1 <= m <= 100`
* `1 <= n <= 20`
* `1 <= target <= m`
* `0 <= houses[i] <= n`
* `1 <= cost[i][j] <= 104` | Represent the counts (odd or even) of vowels with a bitmask. Precompute the prefix xor for the bitmask of vowels and then get the longest valid substring. |
Python3 | Space Optimized | paint-house-iii | 0 | 1 | # Approach\n* Code is self-explanatory\n\n# Complexity\n- Time complexity: $$O(M \\cdot T \\cdot N^2)$$\n\n- Space complexity: $$O(T \\cdot N)$$\n\n# Code\n```\nclass Solution:\n def minCost(self, houses: List[int], cost: List[List[int]], m: int, n: int, target: int) -> int:\n dp = [[+inf for _ in range(n)] for _ in range(target+1)]\n # [number_of_neighbourhoods][last_color] = min_cost\n for color in range(n):\n dp[0][color] = 0\n for i in range(m):\n new_dp = [[+inf for _ in range(n)] for _ in range(m+1)]\n for prev_neighbourhoods in range(target+1):\n for prev_color in range(n):\n if houses[i]-1 == -1:\n for color in range(n):\n neighbourhoods = max(1, prev_neighbourhoods + (prev_color != color))\n if neighbourhoods > target: continue\n new_dp[neighbourhoods][color] = min(\n new_dp[neighbourhoods][color],\n dp[prev_neighbourhoods][prev_color] + cost[i][color],\n )\n else:\n color = houses[i]-1\n neighbourhoods = max(1, prev_neighbourhoods + (prev_color != color))\n if neighbourhoods > target: continue\n new_dp[neighbourhoods][color] = min(\n new_dp[neighbourhoods][color],\n dp[prev_neighbourhoods][prev_color],\n )\n dp = new_dp\n ans = min(dp[target])\n return ans if ans != +inf else -1\n``` | 1 | You are given a list of `preferences` for `n` friends, where `n` is always **even**.
For each person `i`, `preferences[i]` contains a list of friends **sorted** in the **order of preference**. In other words, a friend earlier in the list is more preferred than a friend later in the list. Friends in each list are denoted by integers from `0` to `n-1`.
All the friends are divided into pairs. The pairings are given in a list `pairs`, where `pairs[i] = [xi, yi]` denotes `xi` is paired with `yi` and `yi` is paired with `xi`.
However, this pairing may cause some of the friends to be unhappy. A friend `x` is unhappy if `x` is paired with `y` and there exists a friend `u` who is paired with `v` but:
* `x` prefers `u` over `y`, and
* `u` prefers `x` over `v`.
Return _the number of unhappy friends_.
**Example 1:**
**Input:** n = 4, preferences = \[\[1, 2, 3\], \[3, 2, 0\], \[3, 1, 0\], \[1, 2, 0\]\], pairs = \[\[0, 1\], \[2, 3\]\]
**Output:** 2
**Explanation:**
Friend 1 is unhappy because:
- 1 is paired with 0 but prefers 3 over 0, and
- 3 prefers 1 over 2.
Friend 3 is unhappy because:
- 3 is paired with 2 but prefers 1 over 2, and
- 1 prefers 3 over 0.
Friends 0 and 2 are happy.
**Example 2:**
**Input:** n = 2, preferences = \[\[1\], \[0\]\], pairs = \[\[1, 0\]\]
**Output:** 0
**Explanation:** Both friends 0 and 1 are happy.
**Example 3:**
**Input:** n = 4, preferences = \[\[1, 3, 2\], \[2, 3, 0\], \[1, 3, 0\], \[0, 2, 1\]\], pairs = \[\[1, 3\], \[0, 2\]\]
**Output:** 4
**Constraints:**
* `2 <= n <= 500`
* `n` is even.
* `preferences.length == n`
* `preferences[i].length == n - 1`
* `0 <= preferences[i][j] <= n - 1`
* `preferences[i]` does not contain `i`.
* All values in `preferences[i]` are unique.
* `pairs.length == n/2`
* `pairs[i].length == 2`
* `xi != yi`
* `0 <= xi, yi <= n - 1`
* Each person is contained in **exactly one** pair. | Use Dynamic programming. Define dp[i][j][k] as the minimum cost where we have k neighborhoods in the first i houses and the i-th house is painted with the color j. |
Beats 54.86% || Final prices with a special discount in a shop | final-prices-with-a-special-discount-in-a-shop | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def finalPrices(self, prices: List[int]) -> List[int]:\n ans=[]\n for i in range(len(prices)):\n for j in range(1,len(prices)):\n if j>i and prices[j]<=prices[i]:\n ans.append(prices[i]-prices[j])\n break\n else:\n ans.append(prices[i])\n return ans\n``` | 1 | You are given an integer array `prices` where `prices[i]` is the price of the `ith` item in a shop.
There is a special discount for items in the shop. If you buy the `ith` item, then you will receive a discount equivalent to `prices[j]` where `j` is the minimum index such that `j > i` and `prices[j] <= prices[i]`. Otherwise, you will not receive any discount at all.
Return an integer array `answer` where `answer[i]` is the final price you will pay for the `ith` item of the shop, considering the special discount.
**Example 1:**
**Input:** prices = \[8,4,6,2,3\]
**Output:** \[4,2,4,2,3\]
**Explanation:**
For item 0 with price\[0\]=8 you will receive a discount equivalent to prices\[1\]=4, therefore, the final price you will pay is 8 - 4 = 4.
For item 1 with price\[1\]=4 you will receive a discount equivalent to prices\[3\]=2, therefore, the final price you will pay is 4 - 2 = 2.
For item 2 with price\[2\]=6 you will receive a discount equivalent to prices\[3\]=2, therefore, the final price you will pay is 6 - 2 = 4.
For items 3 and 4 you will not receive any discount at all.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** \[1,2,3,4,5\]
**Explanation:** In this case, for all items, you will not receive any discount at all.
**Example 3:**
**Input:** prices = \[10,1,1,6\]
**Output:** \[9,0,1,6\]
**Constraints:**
* `1 <= prices.length <= 500`
* `1 <= prices[i] <= 1000`
The left subtree of a node contains only nodes with keys less than the node's key. The right subtree of a node contains only nodes with keys greater than the node's key. Both the left and right subtrees must also be binary search trees. | Create a datastructure with 4 parameters: (sum, isBST, maxLeft, minLeft). In each node compute theses parameters, following the conditions of a Binary Search Tree. |
Python 3, One-pass, Visual explain, Monotonous stack | final-prices-with-a-special-discount-in-a-shop | 0 | 1 | At this point, when you see this post, you may have already know how to code using the Monotonous Increasing Stack stragegy. This post has the same code as you saw from other posts. However, as an engineer like me, I\'d like to actually see how the Monotonous Stack works visually. So here you go, below are some diagrams to illustrate it thruough the example *prices = [8,4,6,2,3]*. You will see the stack status changes, and how the elements are updated accordingly.\nA couple of highlights about the below code though:\n* Implementing the Monotonous Increasing Stack stragegy\n* The stack stores indices\n\n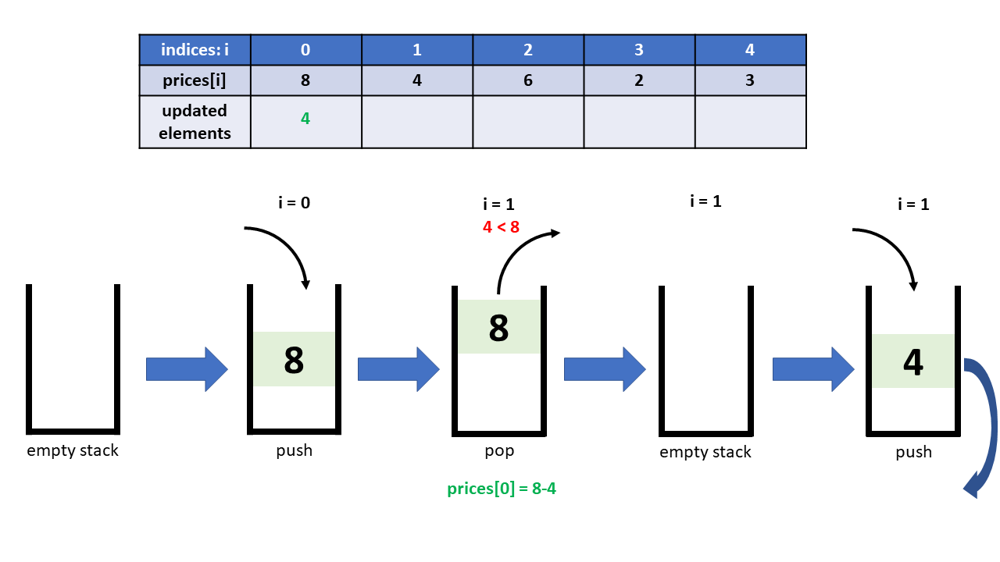\n\n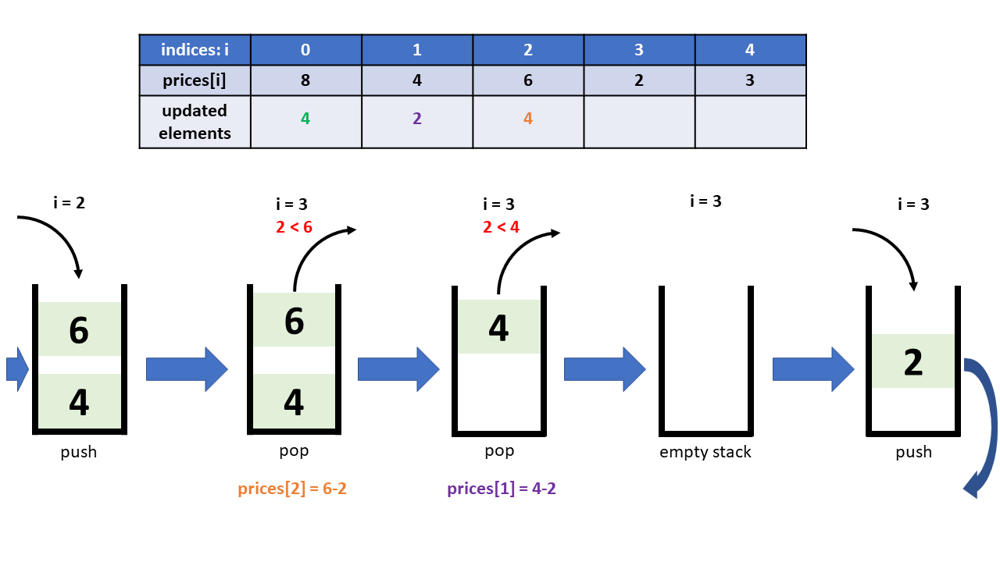\n\n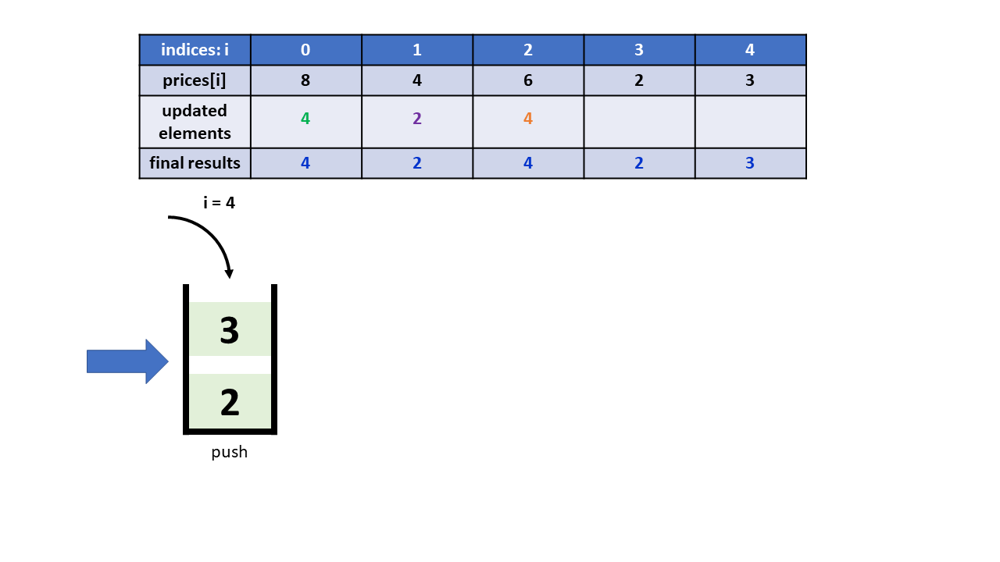\n\n~~~\nclass Solution:\n def finalPrices(self, prices: List[int]) -> List[int]:\n stack = []\n for i in range(len(prices)):\n while stack and (prices[stack[-1]] >= prices[i]):\n prices[stack.pop()] -= prices[i]\n stack.append(i)\n return prices\n~~~\n\n#Runtime: 36 ms, faster than 100.00% of Python3 online submissions for Final Prices With a Special Discount in a Shop.\n#Memory Usage: 14.3 MB, less than 59.61% of Python3 online submissions for Final Prices With a Special Discount in a Shop. | 37 | You are given an integer array `prices` where `prices[i]` is the price of the `ith` item in a shop.
There is a special discount for items in the shop. If you buy the `ith` item, then you will receive a discount equivalent to `prices[j]` where `j` is the minimum index such that `j > i` and `prices[j] <= prices[i]`. Otherwise, you will not receive any discount at all.
Return an integer array `answer` where `answer[i]` is the final price you will pay for the `ith` item of the shop, considering the special discount.
**Example 1:**
**Input:** prices = \[8,4,6,2,3\]
**Output:** \[4,2,4,2,3\]
**Explanation:**
For item 0 with price\[0\]=8 you will receive a discount equivalent to prices\[1\]=4, therefore, the final price you will pay is 8 - 4 = 4.
For item 1 with price\[1\]=4 you will receive a discount equivalent to prices\[3\]=2, therefore, the final price you will pay is 4 - 2 = 2.
For item 2 with price\[2\]=6 you will receive a discount equivalent to prices\[3\]=2, therefore, the final price you will pay is 6 - 2 = 4.
For items 3 and 4 you will not receive any discount at all.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** \[1,2,3,4,5\]
**Explanation:** In this case, for all items, you will not receive any discount at all.
**Example 3:**
**Input:** prices = \[10,1,1,6\]
**Output:** \[9,0,1,6\]
**Constraints:**
* `1 <= prices.length <= 500`
* `1 <= prices[i] <= 1000`
The left subtree of a node contains only nodes with keys less than the node's key. The right subtree of a node contains only nodes with keys greater than the node's key. Both the left and right subtrees must also be binary search trees. | Create a datastructure with 4 parameters: (sum, isBST, maxLeft, minLeft). In each node compute theses parameters, following the conditions of a Binary Search Tree. |
[Python]||O(N^2) | final-prices-with-a-special-discount-in-a-shop | 0 | 1 | Time Complexcity O(N^2)\nSpace Complexcity O(N)\n```\nclass Solution:\n def finalPrices(self, prices: List[int]) -> List[int]:\n ans=[]\n for i in range(len(prices)-1):\n flag=False\n for j in range(i+1,len(prices)):\n if prices[i]>=prices[j]:\n ans.append(abs(prices[i]-prices[j]))\n flag=True\n break\n if flag==False:\n ans.append(prices[i])\n \n \n ans.append(prices[-1])\n return ans\n \n```\n**pls voter if helpfull** | 3 | You are given an integer array `prices` where `prices[i]` is the price of the `ith` item in a shop.
There is a special discount for items in the shop. If you buy the `ith` item, then you will receive a discount equivalent to `prices[j]` where `j` is the minimum index such that `j > i` and `prices[j] <= prices[i]`. Otherwise, you will not receive any discount at all.
Return an integer array `answer` where `answer[i]` is the final price you will pay for the `ith` item of the shop, considering the special discount.
**Example 1:**
**Input:** prices = \[8,4,6,2,3\]
**Output:** \[4,2,4,2,3\]
**Explanation:**
For item 0 with price\[0\]=8 you will receive a discount equivalent to prices\[1\]=4, therefore, the final price you will pay is 8 - 4 = 4.
For item 1 with price\[1\]=4 you will receive a discount equivalent to prices\[3\]=2, therefore, the final price you will pay is 4 - 2 = 2.
For item 2 with price\[2\]=6 you will receive a discount equivalent to prices\[3\]=2, therefore, the final price you will pay is 6 - 2 = 4.
For items 3 and 4 you will not receive any discount at all.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** \[1,2,3,4,5\]
**Explanation:** In this case, for all items, you will not receive any discount at all.
**Example 3:**
**Input:** prices = \[10,1,1,6\]
**Output:** \[9,0,1,6\]
**Constraints:**
* `1 <= prices.length <= 500`
* `1 <= prices[i] <= 1000`
The left subtree of a node contains only nodes with keys less than the node's key. The right subtree of a node contains only nodes with keys greater than the node's key. Both the left and right subtrees must also be binary search trees. | Create a datastructure with 4 parameters: (sum, isBST, maxLeft, minLeft). In each node compute theses parameters, following the conditions of a Binary Search Tree. |
Python easy soln | subrectangle-queries | 0 | 1 | # Very easy soln\n\n# Code\n```\nclass SubrectangleQueries:\n\n def __init__(self, rectangle: List[List[int]]):\n self.r=rectangle\n\n def updateSubrectangle(self, row1: int, col1: int, row2: int, col2: int, newValue: int) -> None:\n for i in range(row1,row2+1):\n for j in range(col1,col2+1):\n self.r[i][j]=newValue\n\n def getValue(self, row: int, col: int) -> int:\n return self.r[row][col]\n``` | 1 | Implement the class `SubrectangleQueries` which receives a `rows x cols` rectangle as a matrix of integers in the constructor and supports two methods:
1. `updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)`
* Updates all values with `newValue` in the subrectangle whose upper left coordinate is `(row1,col1)` and bottom right coordinate is `(row2,col2)`.
2. `getValue(int row, int col)`
* Returns the current value of the coordinate `(row,col)` from the rectangle.
**Example 1:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue ", "getValue "\]
\[\[\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]\],\[0,2\],\[0,0,3,2,5\],\[0,2\],\[3,1\],\[3,0,3,2,10\],\[3,1\],\[0,2\]\]
**Output**
\[null,1,null,5,5,null,10,5\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]);
// The initial rectangle (4x3) looks like:
// 1 2 1
// 4 3 4
// 3 2 1
// 1 1 1
subrectangleQueries.getValue(0, 2); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 5 5 5
subrectangleQueries.getValue(0, 2); // return 5
subrectangleQueries.getValue(3, 1); // return 5
subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 10 10 10
subrectangleQueries.getValue(3, 1); // return 10
subrectangleQueries.getValue(0, 2); // return 5
**Example 2:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue "\]
\[\[\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]\],\[0,0\],\[0,0,2,2,100\],\[0,0\],\[2,2\],\[1,1,2,2,20\],\[2,2\]\]
**Output**
\[null,1,null,100,100,null,20\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]);
subrectangleQueries.getValue(0, 0); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100);
subrectangleQueries.getValue(0, 0); // return 100
subrectangleQueries.getValue(2, 2); // return 100
subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20);
subrectangleQueries.getValue(2, 2); // return 20
**Constraints:**
* There will be at most `500` operations considering both methods: `updateSubrectangle` and `getValue`.
* `1 <= rows, cols <= 100`
* `rows == rectangle.length`
* `cols == rectangle[i].length`
* `0 <= row1 <= row2 < rows`
* `0 <= col1 <= col2 < cols`
* `1 <= newValue, rectangle[i][j] <= 10^9`
* `0 <= row < rows`
* `0 <= col < cols` | Use binary search for optimization or simply brute force. |
Python easy soln | subrectangle-queries | 0 | 1 | # Very easy soln\n\n# Code\n```\nclass SubrectangleQueries:\n\n def __init__(self, rectangle: List[List[int]]):\n self.r=rectangle\n\n def updateSubrectangle(self, row1: int, col1: int, row2: int, col2: int, newValue: int) -> None:\n for i in range(row1,row2+1):\n for j in range(col1,col2+1):\n self.r[i][j]=newValue\n\n def getValue(self, row: int, col: int) -> int:\n return self.r[row][col]\n``` | 1 | Given a square matrix `mat`, return the sum of the matrix diagonals.
Only include the sum of all the elements on the primary diagonal and all the elements on the secondary diagonal that are not part of the primary diagonal.
**Example 1:**
**Input:** mat = \[\[**1**,2,**3**\],
\[4,**5**,6\],
\[**7**,8,**9**\]\]
**Output:** 25
**Explanation:** Diagonals sum: 1 + 5 + 9 + 3 + 7 = 25
Notice that element mat\[1\]\[1\] = 5 is counted only once.
**Example 2:**
**Input:** mat = \[\[**1**,1,1,**1**\],
\[1,**1**,**1**,1\],
\[1,**1**,**1**,1\],
\[**1**,1,1,**1**\]\]
**Output:** 8
**Example 3:**
**Input:** mat = \[\[**5**\]\]
**Output:** 5
**Constraints:**
* `n == mat.length == mat[i].length`
* `1 <= n <= 100`
* `1 <= mat[i][j] <= 100` | Use brute force to update a rectangle and, response to the queries in O(1). |
「🙏Python3」🧼Clean-Intuitive🧠 || O(R * C) || Thanks for reading | subrectangle-queries | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nYou want to find the range of the 2D Matrix that you need to change to the `newValue`. The rectangle will be\n\n***Top-Left*** \n\u300C`(row1, col1)` -----------\n------------- `(row2, col2)`\u300D***Bot-Right***\n\n---\n\n# Complexity\n- \u2705\u231B Time complexity: `O(R * C)`\u231B --> The worst case scenario you have to change the **entire rectangle** to the `newValue`.\n \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n\n- \u2705\uD83D\uDCBE Space complexity: `O(1)` \uD83D\uDCBE --> To `getValue`. \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# \uD83E\uDDFCCode\uD83E\uDDFC\n```\nclass SubrectangleQueries:\n\n def __init__(self, rectangle: List[List[int]]):\n self.rec = rectangle\n\n def updateSubrectangle(self, row1: int, col1: int, row2: int, col2: int, newValue: int) -> None:\n # from 1st row ~ last row\n for r in range(row1, row2+1): \n # from 1st col ~ last col\n for c in range(col1, col2+1):\n # change rectangle index (r,c) value = newValue\n self.rec[r][c] = newValue\n \n\n def getValue(self, row: int, col: int) -> int:\n return self.rec[row][col]\n | 4 | Implement the class `SubrectangleQueries` which receives a `rows x cols` rectangle as a matrix of integers in the constructor and supports two methods:
1. `updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)`
* Updates all values with `newValue` in the subrectangle whose upper left coordinate is `(row1,col1)` and bottom right coordinate is `(row2,col2)`.
2. `getValue(int row, int col)`
* Returns the current value of the coordinate `(row,col)` from the rectangle.
**Example 1:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue ", "getValue "\]
\[\[\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]\],\[0,2\],\[0,0,3,2,5\],\[0,2\],\[3,1\],\[3,0,3,2,10\],\[3,1\],\[0,2\]\]
**Output**
\[null,1,null,5,5,null,10,5\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]);
// The initial rectangle (4x3) looks like:
// 1 2 1
// 4 3 4
// 3 2 1
// 1 1 1
subrectangleQueries.getValue(0, 2); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 5 5 5
subrectangleQueries.getValue(0, 2); // return 5
subrectangleQueries.getValue(3, 1); // return 5
subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 10 10 10
subrectangleQueries.getValue(3, 1); // return 10
subrectangleQueries.getValue(0, 2); // return 5
**Example 2:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue "\]
\[\[\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]\],\[0,0\],\[0,0,2,2,100\],\[0,0\],\[2,2\],\[1,1,2,2,20\],\[2,2\]\]
**Output**
\[null,1,null,100,100,null,20\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]);
subrectangleQueries.getValue(0, 0); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100);
subrectangleQueries.getValue(0, 0); // return 100
subrectangleQueries.getValue(2, 2); // return 100
subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20);
subrectangleQueries.getValue(2, 2); // return 20
**Constraints:**
* There will be at most `500` operations considering both methods: `updateSubrectangle` and `getValue`.
* `1 <= rows, cols <= 100`
* `rows == rectangle.length`
* `cols == rectangle[i].length`
* `0 <= row1 <= row2 < rows`
* `0 <= col1 <= col2 < cols`
* `1 <= newValue, rectangle[i][j] <= 10^9`
* `0 <= row < rows`
* `0 <= col < cols` | Use binary search for optimization or simply brute force. |
「🙏Python3」🧼Clean-Intuitive🧠 || O(R * C) || Thanks for reading | subrectangle-queries | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nYou want to find the range of the 2D Matrix that you need to change to the `newValue`. The rectangle will be\n\n***Top-Left*** \n\u300C`(row1, col1)` -----------\n------------- `(row2, col2)`\u300D***Bot-Right***\n\n---\n\n# Complexity\n- \u2705\u231B Time complexity: `O(R * C)`\u231B --> The worst case scenario you have to change the **entire rectangle** to the `newValue`.\n \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n\n- \u2705\uD83D\uDCBE Space complexity: `O(1)` \uD83D\uDCBE --> To `getValue`. \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# \uD83E\uDDFCCode\uD83E\uDDFC\n```\nclass SubrectangleQueries:\n\n def __init__(self, rectangle: List[List[int]]):\n self.rec = rectangle\n\n def updateSubrectangle(self, row1: int, col1: int, row2: int, col2: int, newValue: int) -> None:\n # from 1st row ~ last row\n for r in range(row1, row2+1): \n # from 1st col ~ last col\n for c in range(col1, col2+1):\n # change rectangle index (r,c) value = newValue\n self.rec[r][c] = newValue\n \n\n def getValue(self, row: int, col: int) -> int:\n return self.rec[row][col]\n | 4 | Given a square matrix `mat`, return the sum of the matrix diagonals.
Only include the sum of all the elements on the primary diagonal and all the elements on the secondary diagonal that are not part of the primary diagonal.
**Example 1:**
**Input:** mat = \[\[**1**,2,**3**\],
\[4,**5**,6\],
\[**7**,8,**9**\]\]
**Output:** 25
**Explanation:** Diagonals sum: 1 + 5 + 9 + 3 + 7 = 25
Notice that element mat\[1\]\[1\] = 5 is counted only once.
**Example 2:**
**Input:** mat = \[\[**1**,1,1,**1**\],
\[1,**1**,**1**,1\],
\[1,**1**,**1**,1\],
\[**1**,1,1,**1**\]\]
**Output:** 8
**Example 3:**
**Input:** mat = \[\[**5**\]\]
**Output:** 5
**Constraints:**
* `n == mat.length == mat[i].length`
* `1 <= n <= 100`
* `1 <= mat[i][j] <= 100` | Use brute force to update a rectangle and, response to the queries in O(1). |
Easy, Intiutive Python, Faster than 99% | subrectangle-queries | 0 | 1 | Idea: Updating the rectangle is an expensive write operation. Instead we simply keep a store of all subsequent updates and look through the store to check whether the value has been updated. If not, we return the value from the original rectangle.\n```\nclass SubrectangleQueries:\n\n def __init__(self, rectangle: List[List[int]]):\n self.rectangle = rectangle\n self.ops = []\n\n def updateSubrectangle(self, row1: int, col1: int, row2: int, col2: int, newValue: int) -> None:\n self.ops.append((row1, col1, row2, col2, newValue))\n\n def getValue(self, row: int, col: int) -> int:\n for row1, col1, row2, col2, val in reversed(self.ops):\n if row >= row1 and col >= col1 and row <= row2 and col <= col2:\n return val\n return self.rectangle[row][col]\n``` | 9 | Implement the class `SubrectangleQueries` which receives a `rows x cols` rectangle as a matrix of integers in the constructor and supports two methods:
1. `updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)`
* Updates all values with `newValue` in the subrectangle whose upper left coordinate is `(row1,col1)` and bottom right coordinate is `(row2,col2)`.
2. `getValue(int row, int col)`
* Returns the current value of the coordinate `(row,col)` from the rectangle.
**Example 1:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue ", "getValue "\]
\[\[\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]\],\[0,2\],\[0,0,3,2,5\],\[0,2\],\[3,1\],\[3,0,3,2,10\],\[3,1\],\[0,2\]\]
**Output**
\[null,1,null,5,5,null,10,5\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]);
// The initial rectangle (4x3) looks like:
// 1 2 1
// 4 3 4
// 3 2 1
// 1 1 1
subrectangleQueries.getValue(0, 2); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 5 5 5
subrectangleQueries.getValue(0, 2); // return 5
subrectangleQueries.getValue(3, 1); // return 5
subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 10 10 10
subrectangleQueries.getValue(3, 1); // return 10
subrectangleQueries.getValue(0, 2); // return 5
**Example 2:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue "\]
\[\[\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]\],\[0,0\],\[0,0,2,2,100\],\[0,0\],\[2,2\],\[1,1,2,2,20\],\[2,2\]\]
**Output**
\[null,1,null,100,100,null,20\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]);
subrectangleQueries.getValue(0, 0); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100);
subrectangleQueries.getValue(0, 0); // return 100
subrectangleQueries.getValue(2, 2); // return 100
subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20);
subrectangleQueries.getValue(2, 2); // return 20
**Constraints:**
* There will be at most `500` operations considering both methods: `updateSubrectangle` and `getValue`.
* `1 <= rows, cols <= 100`
* `rows == rectangle.length`
* `cols == rectangle[i].length`
* `0 <= row1 <= row2 < rows`
* `0 <= col1 <= col2 < cols`
* `1 <= newValue, rectangle[i][j] <= 10^9`
* `0 <= row < rows`
* `0 <= col < cols` | Use binary search for optimization or simply brute force. |
Easy, Intiutive Python, Faster than 99% | subrectangle-queries | 0 | 1 | Idea: Updating the rectangle is an expensive write operation. Instead we simply keep a store of all subsequent updates and look through the store to check whether the value has been updated. If not, we return the value from the original rectangle.\n```\nclass SubrectangleQueries:\n\n def __init__(self, rectangle: List[List[int]]):\n self.rectangle = rectangle\n self.ops = []\n\n def updateSubrectangle(self, row1: int, col1: int, row2: int, col2: int, newValue: int) -> None:\n self.ops.append((row1, col1, row2, col2, newValue))\n\n def getValue(self, row: int, col: int) -> int:\n for row1, col1, row2, col2, val in reversed(self.ops):\n if row >= row1 and col >= col1 and row <= row2 and col <= col2:\n return val\n return self.rectangle[row][col]\n``` | 9 | Given a square matrix `mat`, return the sum of the matrix diagonals.
Only include the sum of all the elements on the primary diagonal and all the elements on the secondary diagonal that are not part of the primary diagonal.
**Example 1:**
**Input:** mat = \[\[**1**,2,**3**\],
\[4,**5**,6\],
\[**7**,8,**9**\]\]
**Output:** 25
**Explanation:** Diagonals sum: 1 + 5 + 9 + 3 + 7 = 25
Notice that element mat\[1\]\[1\] = 5 is counted only once.
**Example 2:**
**Input:** mat = \[\[**1**,1,1,**1**\],
\[1,**1**,**1**,1\],
\[1,**1**,**1**,1\],
\[**1**,1,1,**1**\]\]
**Output:** 8
**Example 3:**
**Input:** mat = \[\[**5**\]\]
**Output:** 5
**Constraints:**
* `n == mat.length == mat[i].length`
* `1 <= n <= 100`
* `1 <= mat[i][j] <= 100` | Use brute force to update a rectangle and, response to the queries in O(1). |
easy solution to understand python3 | subrectangle-queries | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass SubrectangleQueries:\n\n def __init__(self, rectangle: List[List[int]]):\n self.rectangle = rectangle\n \n\n def updateSubrectangle(self, row1: int, col1: int, row2: int, col2: int, newValue: int) -> None:\n for i in range(row1,row2+1):\n for j in range(col1, col2+1):\n self.rectangle[i][j] = newValue\n \n\n def getValue(self, row: int, col: int) -> int:\n return self.rectangle[row][col]\n\n\n# Your SubrectangleQueries object will be instantiated and called as such:\n# obj = SubrectangleQueries(rectangle)\n# obj.updateSubrectangle(row1,col1,row2,col2,newValue)\n# param_2 = obj.getValue(row,col)\n``` | 1 | Implement the class `SubrectangleQueries` which receives a `rows x cols` rectangle as a matrix of integers in the constructor and supports two methods:
1. `updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)`
* Updates all values with `newValue` in the subrectangle whose upper left coordinate is `(row1,col1)` and bottom right coordinate is `(row2,col2)`.
2. `getValue(int row, int col)`
* Returns the current value of the coordinate `(row,col)` from the rectangle.
**Example 1:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue ", "getValue "\]
\[\[\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]\],\[0,2\],\[0,0,3,2,5\],\[0,2\],\[3,1\],\[3,0,3,2,10\],\[3,1\],\[0,2\]\]
**Output**
\[null,1,null,5,5,null,10,5\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]);
// The initial rectangle (4x3) looks like:
// 1 2 1
// 4 3 4
// 3 2 1
// 1 1 1
subrectangleQueries.getValue(0, 2); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 5 5 5
subrectangleQueries.getValue(0, 2); // return 5
subrectangleQueries.getValue(3, 1); // return 5
subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 10 10 10
subrectangleQueries.getValue(3, 1); // return 10
subrectangleQueries.getValue(0, 2); // return 5
**Example 2:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue "\]
\[\[\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]\],\[0,0\],\[0,0,2,2,100\],\[0,0\],\[2,2\],\[1,1,2,2,20\],\[2,2\]\]
**Output**
\[null,1,null,100,100,null,20\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]);
subrectangleQueries.getValue(0, 0); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100);
subrectangleQueries.getValue(0, 0); // return 100
subrectangleQueries.getValue(2, 2); // return 100
subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20);
subrectangleQueries.getValue(2, 2); // return 20
**Constraints:**
* There will be at most `500` operations considering both methods: `updateSubrectangle` and `getValue`.
* `1 <= rows, cols <= 100`
* `rows == rectangle.length`
* `cols == rectangle[i].length`
* `0 <= row1 <= row2 < rows`
* `0 <= col1 <= col2 < cols`
* `1 <= newValue, rectangle[i][j] <= 10^9`
* `0 <= row < rows`
* `0 <= col < cols` | Use binary search for optimization or simply brute force. |
easy solution to understand python3 | subrectangle-queries | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass SubrectangleQueries:\n\n def __init__(self, rectangle: List[List[int]]):\n self.rectangle = rectangle\n \n\n def updateSubrectangle(self, row1: int, col1: int, row2: int, col2: int, newValue: int) -> None:\n for i in range(row1,row2+1):\n for j in range(col1, col2+1):\n self.rectangle[i][j] = newValue\n \n\n def getValue(self, row: int, col: int) -> int:\n return self.rectangle[row][col]\n\n\n# Your SubrectangleQueries object will be instantiated and called as such:\n# obj = SubrectangleQueries(rectangle)\n# obj.updateSubrectangle(row1,col1,row2,col2,newValue)\n# param_2 = obj.getValue(row,col)\n``` | 1 | Given a square matrix `mat`, return the sum of the matrix diagonals.
Only include the sum of all the elements on the primary diagonal and all the elements on the secondary diagonal that are not part of the primary diagonal.
**Example 1:**
**Input:** mat = \[\[**1**,2,**3**\],
\[4,**5**,6\],
\[**7**,8,**9**\]\]
**Output:** 25
**Explanation:** Diagonals sum: 1 + 5 + 9 + 3 + 7 = 25
Notice that element mat\[1\]\[1\] = 5 is counted only once.
**Example 2:**
**Input:** mat = \[\[**1**,1,1,**1**\],
\[1,**1**,**1**,1\],
\[1,**1**,**1**,1\],
\[**1**,1,1,**1**\]\]
**Output:** 8
**Example 3:**
**Input:** mat = \[\[**5**\]\]
**Output:** 5
**Constraints:**
* `n == mat.length == mat[i].length`
* `1 <= n <= 100`
* `1 <= mat[i][j] <= 100` | Use brute force to update a rectangle and, response to the queries in O(1). |
Beating 95.53% Python Easiest Understandable Solution | subrectangle-queries | 0 | 1 | \n\n# Code\n```\nclass SubrectangleQueries:\n\n def __init__(self, rectangle: List[List[int]]):\n self.rectangle=rectangle\n self.ops=[]\n\n def updateSubrectangle(self, row1: int, col1: int, row2: int, col2: int, newValue: int) -> None:\n self.ops.append((row1,col1,row2,col2,newValue))\n\n def getValue(self, row: int, col: int) -> int:\n for row1,col1,row2,col2, val in reversed(self.ops):\n if row>=row1 and col>=col1 and row<=row2 and col<=col2:\n return val\n return self.rectangle[row][col]\n\n\n# Your SubrectangleQueries object will be instantiated and called as such:\n# obj = SubrectangleQueries(rectangle)\n# obj.updateSubrectangle(row1,col1,row2,col2,newValue)\n# param_2 = obj.getValue(row,col)\n``` | 2 | Implement the class `SubrectangleQueries` which receives a `rows x cols` rectangle as a matrix of integers in the constructor and supports two methods:
1. `updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)`
* Updates all values with `newValue` in the subrectangle whose upper left coordinate is `(row1,col1)` and bottom right coordinate is `(row2,col2)`.
2. `getValue(int row, int col)`
* Returns the current value of the coordinate `(row,col)` from the rectangle.
**Example 1:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue ", "getValue "\]
\[\[\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]\],\[0,2\],\[0,0,3,2,5\],\[0,2\],\[3,1\],\[3,0,3,2,10\],\[3,1\],\[0,2\]\]
**Output**
\[null,1,null,5,5,null,10,5\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]);
// The initial rectangle (4x3) looks like:
// 1 2 1
// 4 3 4
// 3 2 1
// 1 1 1
subrectangleQueries.getValue(0, 2); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 5 5 5
subrectangleQueries.getValue(0, 2); // return 5
subrectangleQueries.getValue(3, 1); // return 5
subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 10 10 10
subrectangleQueries.getValue(3, 1); // return 10
subrectangleQueries.getValue(0, 2); // return 5
**Example 2:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue "\]
\[\[\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]\],\[0,0\],\[0,0,2,2,100\],\[0,0\],\[2,2\],\[1,1,2,2,20\],\[2,2\]\]
**Output**
\[null,1,null,100,100,null,20\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]);
subrectangleQueries.getValue(0, 0); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100);
subrectangleQueries.getValue(0, 0); // return 100
subrectangleQueries.getValue(2, 2); // return 100
subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20);
subrectangleQueries.getValue(2, 2); // return 20
**Constraints:**
* There will be at most `500` operations considering both methods: `updateSubrectangle` and `getValue`.
* `1 <= rows, cols <= 100`
* `rows == rectangle.length`
* `cols == rectangle[i].length`
* `0 <= row1 <= row2 < rows`
* `0 <= col1 <= col2 < cols`
* `1 <= newValue, rectangle[i][j] <= 10^9`
* `0 <= row < rows`
* `0 <= col < cols` | Use binary search for optimization or simply brute force. |
Beating 95.53% Python Easiest Understandable Solution | subrectangle-queries | 0 | 1 | \n\n# Code\n```\nclass SubrectangleQueries:\n\n def __init__(self, rectangle: List[List[int]]):\n self.rectangle=rectangle\n self.ops=[]\n\n def updateSubrectangle(self, row1: int, col1: int, row2: int, col2: int, newValue: int) -> None:\n self.ops.append((row1,col1,row2,col2,newValue))\n\n def getValue(self, row: int, col: int) -> int:\n for row1,col1,row2,col2, val in reversed(self.ops):\n if row>=row1 and col>=col1 and row<=row2 and col<=col2:\n return val\n return self.rectangle[row][col]\n\n\n# Your SubrectangleQueries object will be instantiated and called as such:\n# obj = SubrectangleQueries(rectangle)\n# obj.updateSubrectangle(row1,col1,row2,col2,newValue)\n# param_2 = obj.getValue(row,col)\n``` | 2 | Given a square matrix `mat`, return the sum of the matrix diagonals.
Only include the sum of all the elements on the primary diagonal and all the elements on the secondary diagonal that are not part of the primary diagonal.
**Example 1:**
**Input:** mat = \[\[**1**,2,**3**\],
\[4,**5**,6\],
\[**7**,8,**9**\]\]
**Output:** 25
**Explanation:** Diagonals sum: 1 + 5 + 9 + 3 + 7 = 25
Notice that element mat\[1\]\[1\] = 5 is counted only once.
**Example 2:**
**Input:** mat = \[\[**1**,1,1,**1**\],
\[1,**1**,**1**,1\],
\[1,**1**,**1**,1\],
\[**1**,1,1,**1**\]\]
**Output:** 8
**Example 3:**
**Input:** mat = \[\[**5**\]\]
**Output:** 5
**Constraints:**
* `n == mat.length == mat[i].length`
* `1 <= n <= 100`
* `1 <= mat[i][j] <= 100` | Use brute force to update a rectangle and, response to the queries in O(1). |
[Python] Easier solution | subrectangle-queries | 0 | 1 | \n\n```\nclass SubrectangleQueries(object):\n\n def __init__(self, rectangle):\n self.rectangle = copy.deepcopy(rectangle)\n\n def updateSubrectangle(self, row1, col1, row2, col2, newValue):\n for i in range(row1, row2+1):\n for j in range(col1, col2+1):\n self.rectangle[i][j] = newValue\n\t\t\t\t\n def getValue(self, row, col):\n return self.rectangle[row][col]\n\n\n``` | 10 | Implement the class `SubrectangleQueries` which receives a `rows x cols` rectangle as a matrix of integers in the constructor and supports two methods:
1. `updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)`
* Updates all values with `newValue` in the subrectangle whose upper left coordinate is `(row1,col1)` and bottom right coordinate is `(row2,col2)`.
2. `getValue(int row, int col)`
* Returns the current value of the coordinate `(row,col)` from the rectangle.
**Example 1:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue ", "getValue "\]
\[\[\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]\],\[0,2\],\[0,0,3,2,5\],\[0,2\],\[3,1\],\[3,0,3,2,10\],\[3,1\],\[0,2\]\]
**Output**
\[null,1,null,5,5,null,10,5\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]);
// The initial rectangle (4x3) looks like:
// 1 2 1
// 4 3 4
// 3 2 1
// 1 1 1
subrectangleQueries.getValue(0, 2); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 5 5 5
subrectangleQueries.getValue(0, 2); // return 5
subrectangleQueries.getValue(3, 1); // return 5
subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 10 10 10
subrectangleQueries.getValue(3, 1); // return 10
subrectangleQueries.getValue(0, 2); // return 5
**Example 2:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue "\]
\[\[\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]\],\[0,0\],\[0,0,2,2,100\],\[0,0\],\[2,2\],\[1,1,2,2,20\],\[2,2\]\]
**Output**
\[null,1,null,100,100,null,20\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]);
subrectangleQueries.getValue(0, 0); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100);
subrectangleQueries.getValue(0, 0); // return 100
subrectangleQueries.getValue(2, 2); // return 100
subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20);
subrectangleQueries.getValue(2, 2); // return 20
**Constraints:**
* There will be at most `500` operations considering both methods: `updateSubrectangle` and `getValue`.
* `1 <= rows, cols <= 100`
* `rows == rectangle.length`
* `cols == rectangle[i].length`
* `0 <= row1 <= row2 < rows`
* `0 <= col1 <= col2 < cols`
* `1 <= newValue, rectangle[i][j] <= 10^9`
* `0 <= row < rows`
* `0 <= col < cols` | Use binary search for optimization or simply brute force. |
[Python] Easier solution | subrectangle-queries | 0 | 1 | \n\n```\nclass SubrectangleQueries(object):\n\n def __init__(self, rectangle):\n self.rectangle = copy.deepcopy(rectangle)\n\n def updateSubrectangle(self, row1, col1, row2, col2, newValue):\n for i in range(row1, row2+1):\n for j in range(col1, col2+1):\n self.rectangle[i][j] = newValue\n\t\t\t\t\n def getValue(self, row, col):\n return self.rectangle[row][col]\n\n\n``` | 10 | Given a square matrix `mat`, return the sum of the matrix diagonals.
Only include the sum of all the elements on the primary diagonal and all the elements on the secondary diagonal that are not part of the primary diagonal.
**Example 1:**
**Input:** mat = \[\[**1**,2,**3**\],
\[4,**5**,6\],
\[**7**,8,**9**\]\]
**Output:** 25
**Explanation:** Diagonals sum: 1 + 5 + 9 + 3 + 7 = 25
Notice that element mat\[1\]\[1\] = 5 is counted only once.
**Example 2:**
**Input:** mat = \[\[**1**,1,1,**1**\],
\[1,**1**,**1**,1\],
\[1,**1**,**1**,1\],
\[**1**,1,1,**1**\]\]
**Output:** 8
**Example 3:**
**Input:** mat = \[\[**5**\]\]
**Output:** 5
**Constraints:**
* `n == mat.length == mat[i].length`
* `1 <= n <= 100`
* `1 <= mat[i][j] <= 100` | Use brute force to update a rectangle and, response to the queries in O(1). |
Python + explanation | subrectangle-queries | 0 | 1 | ```\nclass SubrectangleQueries:\n\n def __init__(self, rectangle: List[List[int]]):\n\t\t# make a new dictionary\n self.rec = {}\n\t\t# with enumerate we can iterate through the list rectangle, \n\t\t# taking each row and its index\n for i, row in enumerate(rectangle):\n\t\t\t# we map each row to its index as it`s more space-efficent\n self.rec[i] = row\n \n\n def updateSubrectangle(self, row1: int, col1: int, row2: int, col2: int, newValue: int) -> None:\n\t\t# we want to put new value from row1 to row2, so we iterate through them\n for i in range(row1, row2+1):\n\t\t\t# we put new value only from col1 to col2, but we leave other columns as is\n self.rec[i] = self.rec[i][:col1] + [newValue]*(col2-col1+1) + self.rec[i][col2+1:]\n\n def getValue(self, row: int, col: int) -> int:\n\t\t# take row (of type list) from dictionary rec, take specified col from row\n return self.rec[row][col]\n```\n\nDo you like this solution? | 8 | Implement the class `SubrectangleQueries` which receives a `rows x cols` rectangle as a matrix of integers in the constructor and supports two methods:
1. `updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)`
* Updates all values with `newValue` in the subrectangle whose upper left coordinate is `(row1,col1)` and bottom right coordinate is `(row2,col2)`.
2. `getValue(int row, int col)`
* Returns the current value of the coordinate `(row,col)` from the rectangle.
**Example 1:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue ", "getValue "\]
\[\[\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]\],\[0,2\],\[0,0,3,2,5\],\[0,2\],\[3,1\],\[3,0,3,2,10\],\[3,1\],\[0,2\]\]
**Output**
\[null,1,null,5,5,null,10,5\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]);
// The initial rectangle (4x3) looks like:
// 1 2 1
// 4 3 4
// 3 2 1
// 1 1 1
subrectangleQueries.getValue(0, 2); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 5 5 5
subrectangleQueries.getValue(0, 2); // return 5
subrectangleQueries.getValue(3, 1); // return 5
subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 10 10 10
subrectangleQueries.getValue(3, 1); // return 10
subrectangleQueries.getValue(0, 2); // return 5
**Example 2:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue "\]
\[\[\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]\],\[0,0\],\[0,0,2,2,100\],\[0,0\],\[2,2\],\[1,1,2,2,20\],\[2,2\]\]
**Output**
\[null,1,null,100,100,null,20\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]);
subrectangleQueries.getValue(0, 0); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100);
subrectangleQueries.getValue(0, 0); // return 100
subrectangleQueries.getValue(2, 2); // return 100
subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20);
subrectangleQueries.getValue(2, 2); // return 20
**Constraints:**
* There will be at most `500` operations considering both methods: `updateSubrectangle` and `getValue`.
* `1 <= rows, cols <= 100`
* `rows == rectangle.length`
* `cols == rectangle[i].length`
* `0 <= row1 <= row2 < rows`
* `0 <= col1 <= col2 < cols`
* `1 <= newValue, rectangle[i][j] <= 10^9`
* `0 <= row < rows`
* `0 <= col < cols` | Use binary search for optimization or simply brute force. |
Python + explanation | subrectangle-queries | 0 | 1 | ```\nclass SubrectangleQueries:\n\n def __init__(self, rectangle: List[List[int]]):\n\t\t# make a new dictionary\n self.rec = {}\n\t\t# with enumerate we can iterate through the list rectangle, \n\t\t# taking each row and its index\n for i, row in enumerate(rectangle):\n\t\t\t# we map each row to its index as it`s more space-efficent\n self.rec[i] = row\n \n\n def updateSubrectangle(self, row1: int, col1: int, row2: int, col2: int, newValue: int) -> None:\n\t\t# we want to put new value from row1 to row2, so we iterate through them\n for i in range(row1, row2+1):\n\t\t\t# we put new value only from col1 to col2, but we leave other columns as is\n self.rec[i] = self.rec[i][:col1] + [newValue]*(col2-col1+1) + self.rec[i][col2+1:]\n\n def getValue(self, row: int, col: int) -> int:\n\t\t# take row (of type list) from dictionary rec, take specified col from row\n return self.rec[row][col]\n```\n\nDo you like this solution? | 8 | Given a square matrix `mat`, return the sum of the matrix diagonals.
Only include the sum of all the elements on the primary diagonal and all the elements on the secondary diagonal that are not part of the primary diagonal.
**Example 1:**
**Input:** mat = \[\[**1**,2,**3**\],
\[4,**5**,6\],
\[**7**,8,**9**\]\]
**Output:** 25
**Explanation:** Diagonals sum: 1 + 5 + 9 + 3 + 7 = 25
Notice that element mat\[1\]\[1\] = 5 is counted only once.
**Example 2:**
**Input:** mat = \[\[**1**,1,1,**1**\],
\[1,**1**,**1**,1\],
\[1,**1**,**1**,1\],
\[**1**,1,1,**1**\]\]
**Output:** 8
**Example 3:**
**Input:** mat = \[\[**5**\]\]
**Output:** 5
**Constraints:**
* `n == mat.length == mat[i].length`
* `1 <= n <= 100`
* `1 <= mat[i][j] <= 100` | Use brute force to update a rectangle and, response to the queries in O(1). |
[Python] Similar to BUY AND SELL STOCK 3, Simple DP Solution, Logic and Intuition explained. | find-two-non-overlapping-sub-arrays-each-with-target-sum | 0 | 1 | ```\nclass Solution:\n def minSumOfLengths(self, arr: List[int], target: int) -> int:\n ## RC ##\n ## APPROACH : DP ## \n\t\t## Similar to Leetcode: 123 Best Time To Buy And Sell Stock III ##\n ## LOGIC ##\n ## 1. Like typical subarray sum problem, calculate the valid subarray lengths at that particular index using running/prefix sum\n ## 2. dp will have the minimum subarray length with sum = target found till that index.\n ## 3. now reverse the array and compute the same. (we now have both dp_left and dp_right)\n ## 4. As there should not be any overlaps, we consider minimum found till index - 1 in left side and minimum found from this current index till end on right side. Compute the sum and store in ans.\n\t\t\n\t\t## INTUITION ## (How did I get to know that I have to use dp_left and dp_ right ?)\n\t\t## As we are finding only 2 best cases, if we consider any particular index, one best case can be to its left side , othe best case can be to its right side ##\n \n\t\t## TIME COMPLEXICITY : O(3xN) ##\n\t\t## SPACE COMPLEXICITY : O(N) ##\n \n def get_sub_arrays( arr ):\n lookup = collections.defaultdict(int)\n running_sum = 0\n dp = [float(\'inf\')] * len(arr)\n \n for i, num in enumerate(arr):\n running_sum += num\n if running_sum == target:\n dp[i] = i - 0 + 1\n elif running_sum - target in lookup:\n dp[i] = i - lookup[running_sum - target] + 1\n lookup[running_sum] = i+1\n dp[i] = min( dp[i-1], dp[i] )\n return dp\n \n dp_left = get_sub_arrays( arr ) # from front\n dp_right = get_sub_arrays( arr[::-1] )[::-1] # from backwards\n \n ans = float(\'inf\')\n for i in range( 1, len(arr) ):\n ans = min( ans, dp_left[i-1] + dp_right[i] )\n return ans if( ans != float(\'inf\') ) else -1\n```\nUPVOTE IF YOU LIKE MY SOLUTION. | 54 | You are given an array of integers `arr` and an integer `target`.
You have to find **two non-overlapping sub-arrays** of `arr` each with a sum equal `target`. There can be multiple answers so you have to find an answer where the sum of the lengths of the two sub-arrays is **minimum**.
Return _the minimum sum of the lengths_ of the two required sub-arrays, or return `-1` if you cannot find such two sub-arrays.
**Example 1:**
**Input:** arr = \[3,2,2,4,3\], target = 3
**Output:** 2
**Explanation:** Only two sub-arrays have sum = 3 (\[3\] and \[3\]). The sum of their lengths is 2.
**Example 2:**
**Input:** arr = \[7,3,4,7\], target = 7
**Output:** 2
**Explanation:** Although we have three non-overlapping sub-arrays of sum = 7 (\[7\], \[3,4\] and \[7\]), but we will choose the first and third sub-arrays as the sum of their lengths is 2.
**Example 3:**
**Input:** arr = \[4,3,2,6,2,3,4\], target = 6
**Output:** -1
**Explanation:** We have only one sub-array of sum = 6.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 1000`
* `1 <= target <= 108` | Keep all prefix products of numbers in an array, then calculate the product of last K elements in O(1) complexity. When a zero number is added, clean the array of prefix products. |
[Python] Similar to BUY AND SELL STOCK 3, Simple DP Solution, Logic and Intuition explained. | find-two-non-overlapping-sub-arrays-each-with-target-sum | 0 | 1 | ```\nclass Solution:\n def minSumOfLengths(self, arr: List[int], target: int) -> int:\n ## RC ##\n ## APPROACH : DP ## \n\t\t## Similar to Leetcode: 123 Best Time To Buy And Sell Stock III ##\n ## LOGIC ##\n ## 1. Like typical subarray sum problem, calculate the valid subarray lengths at that particular index using running/prefix sum\n ## 2. dp will have the minimum subarray length with sum = target found till that index.\n ## 3. now reverse the array and compute the same. (we now have both dp_left and dp_right)\n ## 4. As there should not be any overlaps, we consider minimum found till index - 1 in left side and minimum found from this current index till end on right side. Compute the sum and store in ans.\n\t\t\n\t\t## INTUITION ## (How did I get to know that I have to use dp_left and dp_ right ?)\n\t\t## As we are finding only 2 best cases, if we consider any particular index, one best case can be to its left side , othe best case can be to its right side ##\n \n\t\t## TIME COMPLEXICITY : O(3xN) ##\n\t\t## SPACE COMPLEXICITY : O(N) ##\n \n def get_sub_arrays( arr ):\n lookup = collections.defaultdict(int)\n running_sum = 0\n dp = [float(\'inf\')] * len(arr)\n \n for i, num in enumerate(arr):\n running_sum += num\n if running_sum == target:\n dp[i] = i - 0 + 1\n elif running_sum - target in lookup:\n dp[i] = i - lookup[running_sum - target] + 1\n lookup[running_sum] = i+1\n dp[i] = min( dp[i-1], dp[i] )\n return dp\n \n dp_left = get_sub_arrays( arr ) # from front\n dp_right = get_sub_arrays( arr[::-1] )[::-1] # from backwards\n \n ans = float(\'inf\')\n for i in range( 1, len(arr) ):\n ans = min( ans, dp_left[i-1] + dp_right[i] )\n return ans if( ans != float(\'inf\') ) else -1\n```\nUPVOTE IF YOU LIKE MY SOLUTION. | 54 | Given a binary string `s`, you can split `s` into 3 **non-empty** strings `s1`, `s2`, and `s3` where `s1 + s2 + s3 = s`.
Return the number of ways `s` can be split such that the number of ones is the same in `s1`, `s2`, and `s3`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are four ways to split s in 3 parts where each part contain the same number of letters '1'.
"1|010|1 "
"1|01|01 "
"10|10|1 "
"10|1|01 "
**Example 2:**
**Input:** s = "1001 "
**Output:** 0
**Example 3:**
**Input:** s = "0000 "
**Output:** 3
**Explanation:** There are three ways to split s in 3 parts.
"0|0|00 "
"0|00|0 "
"00|0|0 "
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Let's create two arrays prefix and suffix where prefix[i] is the minimum length of sub-array ends before i and has sum = k, suffix[i] is the minimum length of sub-array starting at or after i and has sum = k. The answer we are searching for is min(prefix[i] + suffix[i]) for all values of i from 0 to n-1 where n == arr.length. If you are still stuck with how to build prefix and suffix, you can store for each index i the length of the sub-array starts at i and has sum = k or infinity otherwise, and you can use it to build both prefix and suffix. |
Python - Sliding Window - O(n) with detail comments. | find-two-non-overlapping-sub-arrays-each-with-target-sum | 0 | 1 | \n```python\nclass Solution:\n def minSumOfLengths(self, arr: List[int], target: int) -> int:\n l, windowSum, res = 0, 0, float(\'inf\')\n min_till = [float(\'inf\')] * len(arr) # records smallest lenth of subarry with target sum up till index i.\n for r, num in enumerate(arr): # r:right pointer and index of num in arr\n windowSum += num\n while windowSum > target: \n\t\t\t# when the sum of current window is larger then target, shrink the left end of the window one by one until windowSum <= target\n windowSum -= arr[l]\n l += 1\n\t\t\t# the case when we found a new target sub-array, i.e. current window\n if windowSum == target:\n\t\t\t # length of current window\n curLen = r - l + 1\n\t\t\t\t# min_till[l - 1]: the subarray with min len up till the previous position of left end of the current window: \n\t\t\t\t# avoid overlap with cur window\n\t\t\t\t# new_sum_of_two_subarray = length of current window + the previous min length of target subarray without overlapping\n\t\t\t\t# , if < res, update res.\n res = min(res, curLen + min_till[l - 1])\n\t\t\t\t# Everytime we found a target window, update the min_till of current right end of the window, \n\t\t\t\t# for future use when sum up to new length of sum_of_two_subarray and update the res.\n min_till[r] = min(curLen, min_till[r - 1])\n else:\n\t\t\t# If windowSum < target: window with current arr[r] as right end does not have any target subarry, \n\t\t\t# the min_till[r] doesn\'t get any new minimum update, i.e it equals to previous min_till at index r - 1. \n min_till[r] = min_till[r - 1]\n return res if res < float(\'inf\') else -1\n\t\nTime = O(n): when sliding the window, left and right pointers traverse the array once.\nSpace = O(n): we use one additional list min_till[] to record min length of target subarray till index i. | 6 | You are given an array of integers `arr` and an integer `target`.
You have to find **two non-overlapping sub-arrays** of `arr` each with a sum equal `target`. There can be multiple answers so you have to find an answer where the sum of the lengths of the two sub-arrays is **minimum**.
Return _the minimum sum of the lengths_ of the two required sub-arrays, or return `-1` if you cannot find such two sub-arrays.
**Example 1:**
**Input:** arr = \[3,2,2,4,3\], target = 3
**Output:** 2
**Explanation:** Only two sub-arrays have sum = 3 (\[3\] and \[3\]). The sum of their lengths is 2.
**Example 2:**
**Input:** arr = \[7,3,4,7\], target = 7
**Output:** 2
**Explanation:** Although we have three non-overlapping sub-arrays of sum = 7 (\[7\], \[3,4\] and \[7\]), but we will choose the first and third sub-arrays as the sum of their lengths is 2.
**Example 3:**
**Input:** arr = \[4,3,2,6,2,3,4\], target = 6
**Output:** -1
**Explanation:** We have only one sub-array of sum = 6.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 1000`
* `1 <= target <= 108` | Keep all prefix products of numbers in an array, then calculate the product of last K elements in O(1) complexity. When a zero number is added, clean the array of prefix products. |
Python - Sliding Window - O(n) with detail comments. | find-two-non-overlapping-sub-arrays-each-with-target-sum | 0 | 1 | \n```python\nclass Solution:\n def minSumOfLengths(self, arr: List[int], target: int) -> int:\n l, windowSum, res = 0, 0, float(\'inf\')\n min_till = [float(\'inf\')] * len(arr) # records smallest lenth of subarry with target sum up till index i.\n for r, num in enumerate(arr): # r:right pointer and index of num in arr\n windowSum += num\n while windowSum > target: \n\t\t\t# when the sum of current window is larger then target, shrink the left end of the window one by one until windowSum <= target\n windowSum -= arr[l]\n l += 1\n\t\t\t# the case when we found a new target sub-array, i.e. current window\n if windowSum == target:\n\t\t\t # length of current window\n curLen = r - l + 1\n\t\t\t\t# min_till[l - 1]: the subarray with min len up till the previous position of left end of the current window: \n\t\t\t\t# avoid overlap with cur window\n\t\t\t\t# new_sum_of_two_subarray = length of current window + the previous min length of target subarray without overlapping\n\t\t\t\t# , if < res, update res.\n res = min(res, curLen + min_till[l - 1])\n\t\t\t\t# Everytime we found a target window, update the min_till of current right end of the window, \n\t\t\t\t# for future use when sum up to new length of sum_of_two_subarray and update the res.\n min_till[r] = min(curLen, min_till[r - 1])\n else:\n\t\t\t# If windowSum < target: window with current arr[r] as right end does not have any target subarry, \n\t\t\t# the min_till[r] doesn\'t get any new minimum update, i.e it equals to previous min_till at index r - 1. \n min_till[r] = min_till[r - 1]\n return res if res < float(\'inf\') else -1\n\t\nTime = O(n): when sliding the window, left and right pointers traverse the array once.\nSpace = O(n): we use one additional list min_till[] to record min length of target subarray till index i. | 6 | Given a binary string `s`, you can split `s` into 3 **non-empty** strings `s1`, `s2`, and `s3` where `s1 + s2 + s3 = s`.
Return the number of ways `s` can be split such that the number of ones is the same in `s1`, `s2`, and `s3`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are four ways to split s in 3 parts where each part contain the same number of letters '1'.
"1|010|1 "
"1|01|01 "
"10|10|1 "
"10|1|01 "
**Example 2:**
**Input:** s = "1001 "
**Output:** 0
**Example 3:**
**Input:** s = "0000 "
**Output:** 3
**Explanation:** There are three ways to split s in 3 parts.
"0|0|00 "
"0|00|0 "
"00|0|0 "
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Let's create two arrays prefix and suffix where prefix[i] is the minimum length of sub-array ends before i and has sum = k, suffix[i] is the minimum length of sub-array starting at or after i and has sum = k. The answer we are searching for is min(prefix[i] + suffix[i]) for all values of i from 0 to n-1 where n == arr.length. If you are still stuck with how to build prefix and suffix, you can store for each index i the length of the sub-array starts at i and has sum = k or infinity otherwise, and you can use it to build both prefix and suffix. |
sliding window with two sum idea | find-two-non-overlapping-sub-arrays-each-with-target-sum | 0 | 1 | ```\n # sliding window\n # sliding right each round. then move left dynamically\n # just need two sum, we can use two sum + sliding window + dp\n # where dp is m[i] represent the prvious seen qualified interval length\n # this solves the problem of overlapping\n \n left = right = 0\n n = len(arr)\n cur_sum = 0\n m = [math.inf]*n\n res = math.inf\n \n for right in range(n):\n cur_sum += arr[right]\n while cur_sum >target:\n cur_sum -= arr[left]\n left += 1\n if cur_sum == target:\n if left > 0 and m[left-1] != math.inf:\n res = min(res, m[left-1]+(right-left+1))\n m[right] = min(m[right-1], right-left+1)\n else:\n m[right] = m[right-1]\n \n return res if res != math.inf else -1\n```\n | 0 | You are given an array of integers `arr` and an integer `target`.
You have to find **two non-overlapping sub-arrays** of `arr` each with a sum equal `target`. There can be multiple answers so you have to find an answer where the sum of the lengths of the two sub-arrays is **minimum**.
Return _the minimum sum of the lengths_ of the two required sub-arrays, or return `-1` if you cannot find such two sub-arrays.
**Example 1:**
**Input:** arr = \[3,2,2,4,3\], target = 3
**Output:** 2
**Explanation:** Only two sub-arrays have sum = 3 (\[3\] and \[3\]). The sum of their lengths is 2.
**Example 2:**
**Input:** arr = \[7,3,4,7\], target = 7
**Output:** 2
**Explanation:** Although we have three non-overlapping sub-arrays of sum = 7 (\[7\], \[3,4\] and \[7\]), but we will choose the first and third sub-arrays as the sum of their lengths is 2.
**Example 3:**
**Input:** arr = \[4,3,2,6,2,3,4\], target = 6
**Output:** -1
**Explanation:** We have only one sub-array of sum = 6.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 1000`
* `1 <= target <= 108` | Keep all prefix products of numbers in an array, then calculate the product of last K elements in O(1) complexity. When a zero number is added, clean the array of prefix products. |
sliding window with two sum idea | find-two-non-overlapping-sub-arrays-each-with-target-sum | 0 | 1 | ```\n # sliding window\n # sliding right each round. then move left dynamically\n # just need two sum, we can use two sum + sliding window + dp\n # where dp is m[i] represent the prvious seen qualified interval length\n # this solves the problem of overlapping\n \n left = right = 0\n n = len(arr)\n cur_sum = 0\n m = [math.inf]*n\n res = math.inf\n \n for right in range(n):\n cur_sum += arr[right]\n while cur_sum >target:\n cur_sum -= arr[left]\n left += 1\n if cur_sum == target:\n if left > 0 and m[left-1] != math.inf:\n res = min(res, m[left-1]+(right-left+1))\n m[right] = min(m[right-1], right-left+1)\n else:\n m[right] = m[right-1]\n \n return res if res != math.inf else -1\n```\n | 0 | Given a binary string `s`, you can split `s` into 3 **non-empty** strings `s1`, `s2`, and `s3` where `s1 + s2 + s3 = s`.
Return the number of ways `s` can be split such that the number of ones is the same in `s1`, `s2`, and `s3`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are four ways to split s in 3 parts where each part contain the same number of letters '1'.
"1|010|1 "
"1|01|01 "
"10|10|1 "
"10|1|01 "
**Example 2:**
**Input:** s = "1001 "
**Output:** 0
**Example 3:**
**Input:** s = "0000 "
**Output:** 3
**Explanation:** There are three ways to split s in 3 parts.
"0|0|00 "
"0|00|0 "
"00|0|0 "
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Let's create two arrays prefix and suffix where prefix[i] is the minimum length of sub-array ends before i and has sum = k, suffix[i] is the minimum length of sub-array starting at or after i and has sum = k. The answer we are searching for is min(prefix[i] + suffix[i]) for all values of i from 0 to n-1 where n == arr.length. If you are still stuck with how to build prefix and suffix, you can store for each index i the length of the sub-array starts at i and has sum = k or infinity otherwise, and you can use it to build both prefix and suffix. |
python super easy to understand prefix + suffix | find-two-non-overlapping-sub-arrays-each-with-target-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSumOfLengths(self, arr: List[int], target: int) -> int:\n \n\n prefix = [float("inf")] * len(arr)\n \n index = {0:-1}\n s = 0\n shortest_length = float("inf")\n for i in range(len(arr)):\n s += arr[i]\n if s - target in index:\n shortest_length = min( shortest_length, i - index[s-target])\n \n prefix[i] = shortest_length\n index[s] = i\n \n index = {0:len(arr)}\n s = 0\n shortest_length = float("inf")\n ans = float("inf")\n for i in range(len(arr)-1, 0, -1):\n s += arr[i]\n if s - target in index:\n shortest_length = min( shortest_length, index[s-target]-i)\n ans = min(ans, prefix[i-1]+ shortest_length)\n index[s] = i\n return ans if ans != float("inf") else -1\n \n\n``` | 0 | You are given an array of integers `arr` and an integer `target`.
You have to find **two non-overlapping sub-arrays** of `arr` each with a sum equal `target`. There can be multiple answers so you have to find an answer where the sum of the lengths of the two sub-arrays is **minimum**.
Return _the minimum sum of the lengths_ of the two required sub-arrays, or return `-1` if you cannot find such two sub-arrays.
**Example 1:**
**Input:** arr = \[3,2,2,4,3\], target = 3
**Output:** 2
**Explanation:** Only two sub-arrays have sum = 3 (\[3\] and \[3\]). The sum of their lengths is 2.
**Example 2:**
**Input:** arr = \[7,3,4,7\], target = 7
**Output:** 2
**Explanation:** Although we have three non-overlapping sub-arrays of sum = 7 (\[7\], \[3,4\] and \[7\]), but we will choose the first and third sub-arrays as the sum of their lengths is 2.
**Example 3:**
**Input:** arr = \[4,3,2,6,2,3,4\], target = 6
**Output:** -1
**Explanation:** We have only one sub-array of sum = 6.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 1000`
* `1 <= target <= 108` | Keep all prefix products of numbers in an array, then calculate the product of last K elements in O(1) complexity. When a zero number is added, clean the array of prefix products. |
python super easy to understand prefix + suffix | find-two-non-overlapping-sub-arrays-each-with-target-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSumOfLengths(self, arr: List[int], target: int) -> int:\n \n\n prefix = [float("inf")] * len(arr)\n \n index = {0:-1}\n s = 0\n shortest_length = float("inf")\n for i in range(len(arr)):\n s += arr[i]\n if s - target in index:\n shortest_length = min( shortest_length, i - index[s-target])\n \n prefix[i] = shortest_length\n index[s] = i\n \n index = {0:len(arr)}\n s = 0\n shortest_length = float("inf")\n ans = float("inf")\n for i in range(len(arr)-1, 0, -1):\n s += arr[i]\n if s - target in index:\n shortest_length = min( shortest_length, index[s-target]-i)\n ans = min(ans, prefix[i-1]+ shortest_length)\n index[s] = i\n return ans if ans != float("inf") else -1\n \n\n``` | 0 | Given a binary string `s`, you can split `s` into 3 **non-empty** strings `s1`, `s2`, and `s3` where `s1 + s2 + s3 = s`.
Return the number of ways `s` can be split such that the number of ones is the same in `s1`, `s2`, and `s3`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are four ways to split s in 3 parts where each part contain the same number of letters '1'.
"1|010|1 "
"1|01|01 "
"10|10|1 "
"10|1|01 "
**Example 2:**
**Input:** s = "1001 "
**Output:** 0
**Example 3:**
**Input:** s = "0000 "
**Output:** 3
**Explanation:** There are three ways to split s in 3 parts.
"0|0|00 "
"0|00|0 "
"00|0|0 "
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Let's create two arrays prefix and suffix where prefix[i] is the minimum length of sub-array ends before i and has sum = k, suffix[i] is the minimum length of sub-array starting at or after i and has sum = k. The answer we are searching for is min(prefix[i] + suffix[i]) for all values of i from 0 to n-1 where n == arr.length. If you are still stuck with how to build prefix and suffix, you can store for each index i the length of the sub-array starts at i and has sum = k or infinity otherwise, and you can use it to build both prefix and suffix. |
Python Solution O(n) | Sliding window + DP | find-two-non-overlapping-sub-arrays-each-with-target-sum | 0 | 1 | # Intuition\nUse sliding window to find the substring == target, and use dp to store min length substring (which is equal to target) so far till current index (ie. right pointer of sliding window) \n\nnow lets say ,if you find substring == target, then u take \n\nprevious_min_sm = min(previous_min_sum , current_substring_len + dp[left_pointer-1])\n\n\nHope you understood, me bad at explaining things in words\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSumOfLengths(self, arr: List[int], target: int) -> int:\n dp = [0]*len(arr)\n\n sm = 0\n l = 0\n mn = len(arr)+1\n\n for r in range(len(arr)):\n sm += arr[r]\n\n while l < r and sm > target:\n sm -= arr[l]\n l+=1\n\n if sm == target:\n dp[r] = min(dp[r-1],r-l+1) if dp[r-1] else r-l+1\n \n if dp[l-1]:\n mn = min(mn,dp[l-1]+r-l+1)\n \n else:\n dp[r] = dp[r-1]\n \n return -1 if mn == len(arr)+1 else mn\n\n \n \n``` | 0 | You are given an array of integers `arr` and an integer `target`.
You have to find **two non-overlapping sub-arrays** of `arr` each with a sum equal `target`. There can be multiple answers so you have to find an answer where the sum of the lengths of the two sub-arrays is **minimum**.
Return _the minimum sum of the lengths_ of the two required sub-arrays, or return `-1` if you cannot find such two sub-arrays.
**Example 1:**
**Input:** arr = \[3,2,2,4,3\], target = 3
**Output:** 2
**Explanation:** Only two sub-arrays have sum = 3 (\[3\] and \[3\]). The sum of their lengths is 2.
**Example 2:**
**Input:** arr = \[7,3,4,7\], target = 7
**Output:** 2
**Explanation:** Although we have three non-overlapping sub-arrays of sum = 7 (\[7\], \[3,4\] and \[7\]), but we will choose the first and third sub-arrays as the sum of their lengths is 2.
**Example 3:**
**Input:** arr = \[4,3,2,6,2,3,4\], target = 6
**Output:** -1
**Explanation:** We have only one sub-array of sum = 6.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 1000`
* `1 <= target <= 108` | Keep all prefix products of numbers in an array, then calculate the product of last K elements in O(1) complexity. When a zero number is added, clean the array of prefix products. |
Python Solution O(n) | Sliding window + DP | find-two-non-overlapping-sub-arrays-each-with-target-sum | 0 | 1 | # Intuition\nUse sliding window to find the substring == target, and use dp to store min length substring (which is equal to target) so far till current index (ie. right pointer of sliding window) \n\nnow lets say ,if you find substring == target, then u take \n\nprevious_min_sm = min(previous_min_sum , current_substring_len + dp[left_pointer-1])\n\n\nHope you understood, me bad at explaining things in words\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSumOfLengths(self, arr: List[int], target: int) -> int:\n dp = [0]*len(arr)\n\n sm = 0\n l = 0\n mn = len(arr)+1\n\n for r in range(len(arr)):\n sm += arr[r]\n\n while l < r and sm > target:\n sm -= arr[l]\n l+=1\n\n if sm == target:\n dp[r] = min(dp[r-1],r-l+1) if dp[r-1] else r-l+1\n \n if dp[l-1]:\n mn = min(mn,dp[l-1]+r-l+1)\n \n else:\n dp[r] = dp[r-1]\n \n return -1 if mn == len(arr)+1 else mn\n\n \n \n``` | 0 | Given a binary string `s`, you can split `s` into 3 **non-empty** strings `s1`, `s2`, and `s3` where `s1 + s2 + s3 = s`.
Return the number of ways `s` can be split such that the number of ones is the same in `s1`, `s2`, and `s3`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are four ways to split s in 3 parts where each part contain the same number of letters '1'.
"1|010|1 "
"1|01|01 "
"10|10|1 "
"10|1|01 "
**Example 2:**
**Input:** s = "1001 "
**Output:** 0
**Example 3:**
**Input:** s = "0000 "
**Output:** 3
**Explanation:** There are three ways to split s in 3 parts.
"0|0|00 "
"0|00|0 "
"00|0|0 "
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Let's create two arrays prefix and suffix where prefix[i] is the minimum length of sub-array ends before i and has sum = k, suffix[i] is the minimum length of sub-array starting at or after i and has sum = k. The answer we are searching for is min(prefix[i] + suffix[i]) for all values of i from 0 to n-1 where n == arr.length. If you are still stuck with how to build prefix and suffix, you can store for each index i the length of the sub-array starts at i and has sum = k or infinity otherwise, and you can use it to build both prefix and suffix. |
[Python3] Top-Down DP + Prefix Sum | find-two-non-overlapping-sub-arrays-each-with-target-sum | 0 | 1 | can be shortened but wtv\n# Code\n```\nclass Solution:\n def minSumOfLengths(self, arr: List[int], target: int) -> int:\n \n forward = list(itertools.accumulate(arr)) \n rev = reversed(arr)\n backward = list(itertools.accumulate(rev))\n backward.reverse()\n\n\n fHm = defaultdict(int)\n for index, element in enumerate(forward):\n fHm[element] = index\n\n @cache\n def minFromFront(i): #arr[0], arr[1],...,arr[i] # min sub from this that sum to target\n if i < 0:\n return float(\'inf\')\n if forward[i] == target:\n return i + 1\n \n curr = float(\'inf\')\n compl = forward[i] - target\n if compl in fHm and fHm[compl] < i:\n curr = (i - fHm[compl])\n curr = min(curr, minFromFront(i-1))\n return curr\n\n bHm = defaultdict(int)\n for index in range(len(backward)-1,-1,-1):\n element = backward[index]\n bHm[element] = index\n\n @cache\n def minFromBack(i): #arr[i], arr[i+1], ...\n if i >= len(bHm):\n return float(\'inf\')\n if backward[i] == target:\n return len(backward) - i\n curr = float(\'inf\')\n compl = backward[i] - target\n if compl in bHm and bHm[compl] > i:\n curr = (bHm[compl] - i)\n curr = min(curr, minFromBack(i+1))\n return curr\n\n\n res = float(\'inf\')\n for i in range(len(arr)):\n f = minFromFront(i)\n b = minFromBack(i+1)\n if f != float(\'inf\') and b != float(\'inf\'):\n res = min(res, f + b)\n\n if res == float(\'inf\'): return -1\n return res\n\n \n``` | 0 | You are given an array of integers `arr` and an integer `target`.
You have to find **two non-overlapping sub-arrays** of `arr` each with a sum equal `target`. There can be multiple answers so you have to find an answer where the sum of the lengths of the two sub-arrays is **minimum**.
Return _the minimum sum of the lengths_ of the two required sub-arrays, or return `-1` if you cannot find such two sub-arrays.
**Example 1:**
**Input:** arr = \[3,2,2,4,3\], target = 3
**Output:** 2
**Explanation:** Only two sub-arrays have sum = 3 (\[3\] and \[3\]). The sum of their lengths is 2.
**Example 2:**
**Input:** arr = \[7,3,4,7\], target = 7
**Output:** 2
**Explanation:** Although we have three non-overlapping sub-arrays of sum = 7 (\[7\], \[3,4\] and \[7\]), but we will choose the first and third sub-arrays as the sum of their lengths is 2.
**Example 3:**
**Input:** arr = \[4,3,2,6,2,3,4\], target = 6
**Output:** -1
**Explanation:** We have only one sub-array of sum = 6.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 1000`
* `1 <= target <= 108` | Keep all prefix products of numbers in an array, then calculate the product of last K elements in O(1) complexity. When a zero number is added, clean the array of prefix products. |
[Python3] Top-Down DP + Prefix Sum | find-two-non-overlapping-sub-arrays-each-with-target-sum | 0 | 1 | can be shortened but wtv\n# Code\n```\nclass Solution:\n def minSumOfLengths(self, arr: List[int], target: int) -> int:\n \n forward = list(itertools.accumulate(arr)) \n rev = reversed(arr)\n backward = list(itertools.accumulate(rev))\n backward.reverse()\n\n\n fHm = defaultdict(int)\n for index, element in enumerate(forward):\n fHm[element] = index\n\n @cache\n def minFromFront(i): #arr[0], arr[1],...,arr[i] # min sub from this that sum to target\n if i < 0:\n return float(\'inf\')\n if forward[i] == target:\n return i + 1\n \n curr = float(\'inf\')\n compl = forward[i] - target\n if compl in fHm and fHm[compl] < i:\n curr = (i - fHm[compl])\n curr = min(curr, minFromFront(i-1))\n return curr\n\n bHm = defaultdict(int)\n for index in range(len(backward)-1,-1,-1):\n element = backward[index]\n bHm[element] = index\n\n @cache\n def minFromBack(i): #arr[i], arr[i+1], ...\n if i >= len(bHm):\n return float(\'inf\')\n if backward[i] == target:\n return len(backward) - i\n curr = float(\'inf\')\n compl = backward[i] - target\n if compl in bHm and bHm[compl] > i:\n curr = (bHm[compl] - i)\n curr = min(curr, minFromBack(i+1))\n return curr\n\n\n res = float(\'inf\')\n for i in range(len(arr)):\n f = minFromFront(i)\n b = minFromBack(i+1)\n if f != float(\'inf\') and b != float(\'inf\'):\n res = min(res, f + b)\n\n if res == float(\'inf\'): return -1\n return res\n\n \n``` | 0 | Given a binary string `s`, you can split `s` into 3 **non-empty** strings `s1`, `s2`, and `s3` where `s1 + s2 + s3 = s`.
Return the number of ways `s` can be split such that the number of ones is the same in `s1`, `s2`, and `s3`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are four ways to split s in 3 parts where each part contain the same number of letters '1'.
"1|010|1 "
"1|01|01 "
"10|10|1 "
"10|1|01 "
**Example 2:**
**Input:** s = "1001 "
**Output:** 0
**Example 3:**
**Input:** s = "0000 "
**Output:** 3
**Explanation:** There are three ways to split s in 3 parts.
"0|0|00 "
"0|00|0 "
"00|0|0 "
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Let's create two arrays prefix and suffix where prefix[i] is the minimum length of sub-array ends before i and has sum = k, suffix[i] is the minimum length of sub-array starting at or after i and has sum = k. The answer we are searching for is min(prefix[i] + suffix[i]) for all values of i from 0 to n-1 where n == arr.length. If you are still stuck with how to build prefix and suffix, you can store for each index i the length of the sub-array starts at i and has sum = k or infinity otherwise, and you can use it to build both prefix and suffix. |
✔ Python3 Solution | DP | O(n^3) | allocate-mailboxes | 0 | 1 | # Complexity\n- Time complexity: $$O(n^3)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def minDistance(self, A, K):\n A.sort()\n N = len(A)\n P = [0] + list(accumulate(A))\n dp = [0] + [float(\'inf\')] * N\n for i in range(K):\n for j in range(N - 1, i - 1, -1):\n for k in range(j, i - 1, -1):\n m = (k + j) >> 1\n cost = P[j + 1] + P[k] - 2 * P[m] - A[m] * (j - 2 * m + k + 1)\n dp[j + 1] = min(dp[j + 1], dp[k] + cost)\n return dp[-1]\n``` | 1 | Given the array `houses` where `houses[i]` is the location of the `ith` house along a street and an integer `k`, allocate `k` mailboxes in the street.
Return _the **minimum** total distance between each house and its nearest mailbox_.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** houses = \[1,4,8,10,20\], k = 3
**Output:** 5
**Explanation:** Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
**Example 2:**
**Input:** houses = \[2,3,5,12,18\], k = 2
**Output:** 9
**Explanation:** Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
**Constraints:**
* `1 <= k <= houses.length <= 100`
* `1 <= houses[i] <= 104`
* All the integers of `houses` are **unique**. | Sort the events by the start time and in case of tie by the end time in ascending order. Loop over the sorted events. Attend as much as you can and keep the last day occupied. When you try to attend new event keep in mind the first day you can attend a new event in. |
Python 3 || 7 lines, two-ptr, recursion w/ brief explanation || T/M: 100% / 54% | allocate-mailboxes | 0 | 1 | Here\'s the plan:\nFor a given interval `interval`, we "divide and conquer" until we encounter either one of these base cases:\n1. `k = 1`: If `len(interval)` is odd, we must place the box at the middle house. If `len(interval)` is even, we may place it anywhere at either of the two middle houses. The total distance and then be computed for that box and the houses in`interval`.\n2. `len(interval) == k = 1`: Each house may have its own mailbox so the sum is zero. (Note`right - k + 2`in the code.) There\'s no need to parse up such an interval once its sum is zero.\n\n```\nclass Solution:\n def minDistance(self, houses: List[int], k: int) -> int:\n houses.sort()\n\n @lru_cache(None)\n def dp(left, right, k):\n if k == 1: # <-- 1.\n mid = houses[(left+right) // 2]\n return sum(abs(houses[i] - mid) for i in range(left, right + 1))\n\n return min(dp(left, i, 1) + dp(i+1, right, k - 1) \n for i in range(left, right - k + 2)) # <-- 2.\n\n return dp(0, len(houses)-1, k)\n```\n[https://leetcode.com/problems/allocate-mailboxes/submissions/879441443/?envType=study-plan&id=dynamic-programming-iii](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*^2 * k) and space complexity is *O*(*N*^2 * k), because of the cache.\n | 3 | Given the array `houses` where `houses[i]` is the location of the `ith` house along a street and an integer `k`, allocate `k` mailboxes in the street.
Return _the **minimum** total distance between each house and its nearest mailbox_.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** houses = \[1,4,8,10,20\], k = 3
**Output:** 5
**Explanation:** Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
**Example 2:**
**Input:** houses = \[2,3,5,12,18\], k = 2
**Output:** 9
**Explanation:** Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
**Constraints:**
* `1 <= k <= houses.length <= 100`
* `1 <= houses[i] <= 104`
* All the integers of `houses` are **unique**. | Sort the events by the start time and in case of tie by the end time in ascending order. Loop over the sorted events. Attend as much as you can and keep the last day occupied. When you try to attend new event keep in mind the first day you can attend a new event in. |
Short and simple memoization in Python with explanation, faster than 91% | allocate-mailboxes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal is to divide the `n` houses into `m` groups so that the total distance between houses and mailboxes is minimized. The problem can be typically handled by dynamic programming to explore different ways to grouping. For a group of houses, the best position of the mailbox is the median of the houses. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe solution is implemented with memoization for simplicity. The cost function is also cached for speed up. \n\n# Complexity\n- Time complexity: $$O(n^2m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(nm)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDistance(self, houses: List[int], m: int) -> int:\n @cache\n def cost(l, r):\n median = houses[(l + r) // 2]\n return sum(abs(houses[i] - median) for i in range(l, r))\n\n @cache\n def dp(i, j):\n if i == n:\n return 0\n if j == m:\n return inf\n return min(dp(k, j+1) + cost(i, k) for k in range(i+1, n+1-(m-j-1)))\n\n houses.sort()\n n = len(houses)\n return dp(0, 0) \n``` | 1 | Given the array `houses` where `houses[i]` is the location of the `ith` house along a street and an integer `k`, allocate `k` mailboxes in the street.
Return _the **minimum** total distance between each house and its nearest mailbox_.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** houses = \[1,4,8,10,20\], k = 3
**Output:** 5
**Explanation:** Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
**Example 2:**
**Input:** houses = \[2,3,5,12,18\], k = 2
**Output:** 9
**Explanation:** Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
**Constraints:**
* `1 <= k <= houses.length <= 100`
* `1 <= houses[i] <= 104`
* All the integers of `houses` are **unique**. | Sort the events by the start time and in case of tie by the end time in ascending order. Loop over the sorted events. Attend as much as you can and keep the last day occupied. When you try to attend new event keep in mind the first day you can attend a new event in. |
📌📌 Beginner-Friendly || Easy-to-understand || DP solution 🐍 | allocate-mailboxes | 0 | 1 | ## IDEA:\n* Firstly we will create cost[i][j]. \n* cost[i][j] = total travel distance by putting one mailbox in between i & j houses.\n* It means cost[i][j] is the total travel distance from between houses[i:j] to a mailbox when putting the mailbox among houses[i:j], the best way is put the mail box at median position among houses[i:j].\n\n* Now after creating costs table, we can directly go with the number of mailboxes left and starting index of the free houses.\n* It\'s something like backtracking.\n* We are checking each possible combination of putting the mailbox.\n* Since constraint is low, we can go with O(n^3).\n\n\'\'\'\n\n\tclass Solution:\n def minDistance(self, houses: List[int], k: int) -> int:\n \n n = len(houses)\n houses.sort()\n cost = [[0 for _ in range(n)] for _ in range(n)]\n for i in range(n):\n for j in range(i+1,n):\n mid_house = houses[(i+j)//2]\n for t in range(i,j+1):\n cost[i][j]+= abs(mid_house-houses[t])\n \n @lru_cache(None)\n def dp(k,ind):\n if k==0 and ind==n: return 0\n if k==0 or ind==n: return float(\'inf\')\n res = float(\'inf\')\n for j in range(ind,n):\n c = cost[ind][j]\n res = min(res, c + dp(k-1,j+1))\n \n return res\n \n return dp(k,0)\n\n**Feel free to ask If you have any doubt.**\uD83E\uDD17\n### Thanks and Upvote If you like the idea!!\uD83E\uDD1E | 4 | Given the array `houses` where `houses[i]` is the location of the `ith` house along a street and an integer `k`, allocate `k` mailboxes in the street.
Return _the **minimum** total distance between each house and its nearest mailbox_.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** houses = \[1,4,8,10,20\], k = 3
**Output:** 5
**Explanation:** Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
**Example 2:**
**Input:** houses = \[2,3,5,12,18\], k = 2
**Output:** 9
**Explanation:** Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
**Constraints:**
* `1 <= k <= houses.length <= 100`
* `1 <= houses[i] <= 104`
* All the integers of `houses` are **unique**. | Sort the events by the start time and in case of tie by the end time in ascending order. Loop over the sorted events. Attend as much as you can and keep the last day occupied. When you try to attend new event keep in mind the first day you can attend a new event in. |
python super easy to understand DP top down Dy | allocate-mailboxes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDistance(self, houses: List[int], k: int) -> int:\n houses.sort()\n @functools.lru_cache(None)\n def get_median(l, r):\n if (r-l + 1) % 2:\n return houses[l + (r-l)//2]\n return (houses[l + (r-l)//2] + houses[l + (r-l)//2+1]) //2 \n\n @functools.lru_cache(None)\n def dist(l, r):\n ans = 0\n m = get_median(l,r)\n for j in houses[l:r+1]:\n ans += abs(j - m)\n return ans\n\n @functools.lru_cache(None)\n def dp(i, k):\n if i == len(houses) and k == 0:\n return 0\n if i == len(houses) or k == 0:\n return float("inf")\n ans = float("inf")\n for j in range(i, len(houses)):\n ans = min(ans, dist(i, j) + dp(j+1, k-1))\n return ans\n \n\n\n \n\n return dp(0, k)\n \n \n \n \n``` | 0 | Given the array `houses` where `houses[i]` is the location of the `ith` house along a street and an integer `k`, allocate `k` mailboxes in the street.
Return _the **minimum** total distance between each house and its nearest mailbox_.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** houses = \[1,4,8,10,20\], k = 3
**Output:** 5
**Explanation:** Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
**Example 2:**
**Input:** houses = \[2,3,5,12,18\], k = 2
**Output:** 9
**Explanation:** Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
**Constraints:**
* `1 <= k <= houses.length <= 100`
* `1 <= houses[i] <= 104`
* All the integers of `houses` are **unique**. | Sort the events by the start time and in case of tie by the end time in ascending order. Loop over the sorted events. Attend as much as you can and keep the last day occupied. When you try to attend new event keep in mind the first day you can attend a new event in. |
Dynamic Programming | allocate-mailboxes | 0 | 1 | # Complexity\n- Time complexity: $$O(n^2)$$, where $$n=\\mathrm{houses.length}$$.\n\n- Space complexity: $$O(n^2)$$\n\n# Code\n```\nclass Solution:\n def minDistance(self, houses: List[int], k: int) -> int:\n houses.sort()\n\n @cache\n def minDistanceOneMailbox(l: int, r: int) -> int:\n if l >= r:\n return 0\n \n return houses[r] - houses[l] + minDistanceOneMailbox(l + 1, r - 1)\n\n @cache\n def dp(i: int, kPrime: int) -> int:\n """Returns the answer for houses=houses[:i], k=kPrime"""\n if i == 0:\n return 0\n if kPrime == 0:\n return inf\n \n return min(dp(j, kPrime - 1) + minDistanceOneMailbox(j, i - 1) for j in range(i))\n \n return dp(len(houses), k)\n``` | 0 | Given the array `houses` where `houses[i]` is the location of the `ith` house along a street and an integer `k`, allocate `k` mailboxes in the street.
Return _the **minimum** total distance between each house and its nearest mailbox_.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** houses = \[1,4,8,10,20\], k = 3
**Output:** 5
**Explanation:** Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
**Example 2:**
**Input:** houses = \[2,3,5,12,18\], k = 2
**Output:** 9
**Explanation:** Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
**Constraints:**
* `1 <= k <= houses.length <= 100`
* `1 <= houses[i] <= 104`
* All the integers of `houses` are **unique**. | Sort the events by the start time and in case of tie by the end time in ascending order. Loop over the sorted events. Attend as much as you can and keep the last day occupied. When you try to attend new event keep in mind the first day you can attend a new event in. |
Dynamic programming | allocate-mailboxes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\ndynamic programming\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(mn^2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(mn)\n\n# Code\n```\nclass Solution:\n def minDistance(self, houses: List[int], k: int) -> int:\n houses = sorted(houses)\n n = houses.__len__()\n dyn = [[0 for j in range(k+1)]] + [([0] + [math.inf for j in range(1, k+1)]) for i in range(1,n+1)]\n #print("dyn : ", dyn)\n #print(math.inf * 2)\n \n for j in range(1, k+1):\n for i in range(1, j + 1):\n dyn[i][j] = 0\n \n j = 1\n for i in range(1, n + 1):\n dyn[i][j] = self.cost(houses[0:i])\n \n \n for j in range(2, k+1):\n for i in range(j + 1, n + 1):\n for l in range(1, i):\n if l < j - 1:\n continue\n #print(i, j, l, dyn[l][j-1], houses[l+1:i+1])\n dyn[i][j] = min(dyn[i][j], dyn[l][j-1] + self.cost(houses[l:i]))\n \n #print(i, j, dyn)\n \n return dyn[n][k]\n \n def cost(self,l : List[int]) -> int:\n n = l.__len__()\n if n <= 1:\n return 0\n \n mid = l[n //2]\n \n return sum([abs(x - mid) for x in l]) \n``` | 0 | Given the array `houses` where `houses[i]` is the location of the `ith` house along a street and an integer `k`, allocate `k` mailboxes in the street.
Return _the **minimum** total distance between each house and its nearest mailbox_.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** houses = \[1,4,8,10,20\], k = 3
**Output:** 5
**Explanation:** Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
**Example 2:**
**Input:** houses = \[2,3,5,12,18\], k = 2
**Output:** 9
**Explanation:** Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
**Constraints:**
* `1 <= k <= houses.length <= 100`
* `1 <= houses[i] <= 104`
* All the integers of `houses` are **unique**. | Sort the events by the start time and in case of tie by the end time in ascending order. Loop over the sorted events. Attend as much as you can and keep the last day occupied. When you try to attend new event keep in mind the first day you can attend a new event in. |
[Python] Top - Down Memoization | allocate-mailboxes | 0 | 1 | # Code\n```\nclass Solution:\n def minDistance(self, houses: List[int], k: int) -> int:\n cost = [[0]*101 for _ in range(101)]\n houses.sort()\n\n n = len(houses)\n ## Finding the cummulative distance if I place a mailbox at position x\n ## Many clusers are possible, for each cluster, the median is the optimal choice\n for i in range(n):\n for j in range(i, n):\n for x in range(i, j+1):\n cost[i][j] += abs(houses[(i+j)//2] - houses[x])\n \n ## Top - Down DP\n @lru_cache(None)\n def dfs(start, k):\n if k == 0 and start == n:\n return 0\n if k == 0 or start == n:\n return math.inf\n \n mini = math.inf\n for index in range(start, n):\n mini = min(mini, cost[start][index] + dfs(index + 1, k - 1))\n\n return mini\n \n return dfs(0, k)\n``` | 0 | Given the array `houses` where `houses[i]` is the location of the `ith` house along a street and an integer `k`, allocate `k` mailboxes in the street.
Return _the **minimum** total distance between each house and its nearest mailbox_.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** houses = \[1,4,8,10,20\], k = 3
**Output:** 5
**Explanation:** Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
**Example 2:**
**Input:** houses = \[2,3,5,12,18\], k = 2
**Output:** 9
**Explanation:** Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
**Constraints:**
* `1 <= k <= houses.length <= 100`
* `1 <= houses[i] <= 104`
* All the integers of `houses` are **unique**. | Sort the events by the start time and in case of tie by the end time in ascending order. Loop over the sorted events. Attend as much as you can and keep the last day occupied. When you try to attend new event keep in mind the first day you can attend a new event in. |
Python (Simple DP) | allocate-mailboxes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDistance(self, houses, k):\n n = len(houses)\n\n houses.sort()\n\n @lru_cache(None)\n def func(i,j):\n median = houses[(i+j)//2]\n return sum([abs(houses[k] - median) for k in range(i,j+1)])\n\n @lru_cache(None)\n def dfs(i,k):\n if k == 1:\n return func(i,n-1)\n\n max_val = float("inf")\n\n for j in range(i,n):\n max_val = min(max_val,func(i,j-1) + dfs(j,k-1))\n\n return max_val\n\n return dfs(0,k)\n\n\n\n\n \n\n\n\n \n \n \n\n\n \n\n \n\n``` | 0 | Given the array `houses` where `houses[i]` is the location of the `ith` house along a street and an integer `k`, allocate `k` mailboxes in the street.
Return _the **minimum** total distance between each house and its nearest mailbox_.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** houses = \[1,4,8,10,20\], k = 3
**Output:** 5
**Explanation:** Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
**Example 2:**
**Input:** houses = \[2,3,5,12,18\], k = 2
**Output:** 9
**Explanation:** Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
**Constraints:**
* `1 <= k <= houses.length <= 100`
* `1 <= houses[i] <= 104`
* All the integers of `houses` are **unique**. | Sort the events by the start time and in case of tie by the end time in ascending order. Loop over the sorted events. Attend as much as you can and keep the last day occupied. When you try to attend new event keep in mind the first day you can attend a new event in. |
[Python] Intuition for DP | O(N^3) | allocate-mailboxes | 0 | 1 | As always we need to realize one thing-\n1. Median will always be optimal choice.\n\nNow if you observe, these mail boxes forms a group having some assoicated cost.\nSo we just need to minimize cost to form such k groups. (classic dp problem)\nCost can be calculated using median.\n\n# Code\n```\nclass Solution:\n def minDistance(self, A: List[int], k: int) -> int:\n A.sort()\n n =len(A)\n @cache\n def cost(start,end):\n med = (start+end)//2\n res = 0\n for i in range(start,end+1):\n res += abs(A[med]-A[i])\n return res\n @cache\n def dp(idx,k):\n if(idx==n): return 0\n res = float(\'inf\')\n if(k==0): return res\n for i in range(idx,n-k+1):\n c = cost(idx,i)\n res = min(res,dp(i+1,k-1)+c)\n return res\n return dp(0,k)\n\n \n \n``` | 0 | Given the array `houses` where `houses[i]` is the location of the `ith` house along a street and an integer `k`, allocate `k` mailboxes in the street.
Return _the **minimum** total distance between each house and its nearest mailbox_.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** houses = \[1,4,8,10,20\], k = 3
**Output:** 5
**Explanation:** Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
**Example 2:**
**Input:** houses = \[2,3,5,12,18\], k = 2
**Output:** 9
**Explanation:** Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
**Constraints:**
* `1 <= k <= houses.length <= 100`
* `1 <= houses[i] <= 104`
* All the integers of `houses` are **unique**. | Sort the events by the start time and in case of tie by the end time in ascending order. Loop over the sorted events. Attend as much as you can and keep the last day occupied. When you try to attend new event keep in mind the first day you can attend a new event in. |
Fk this median shit Just Give shit to houses itself in a better way !!!!! | allocate-mailboxes | 0 | 1 | \n# Code\n```\nclass Solution:\n def minDistance(self, hs: List[int], kk: int) -> int:\n hs=[0]+hs\n hs.sort()\n n=len(hs)\n dp=[[-1]*(n+1) for i in range(kk+1)]\n def rec(id,i):\n nonlocal kk\n if i>=n:\n return float("inf")\n if id==kk:\n return sum(hs[i+1:])-(len(hs[i+1:])*hs[i])\n if dp[id][i]!=-1:\n return dp[id][i]\n ans=float("inf")\n for j in range(i+1,len(hs)):\n rs=0\n for k in range(i+1,j):\n if i!=0:\n rs+=min(abs(hs[j]-hs[k]),abs(hs[i]-hs[k]))\n else:\n rs+=abs(hs[j]-hs[k])\n x=rec(id+1,j)\n ans=min(ans,rs+x)\n dp[id][i]=ans\n return ans\n return rec(0,0)\n``` | 0 | Given the array `houses` where `houses[i]` is the location of the `ith` house along a street and an integer `k`, allocate `k` mailboxes in the street.
Return _the **minimum** total distance between each house and its nearest mailbox_.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** houses = \[1,4,8,10,20\], k = 3
**Output:** 5
**Explanation:** Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
**Example 2:**
**Input:** houses = \[2,3,5,12,18\], k = 2
**Output:** 9
**Explanation:** Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
**Constraints:**
* `1 <= k <= houses.length <= 100`
* `1 <= houses[i] <= 104`
* All the integers of `houses` are **unique**. | Sort the events by the start time and in case of tie by the end time in ascending order. Loop over the sorted events. Attend as much as you can and keep the last day occupied. When you try to attend new event keep in mind the first day you can attend a new event in. |
Solutions in C++ and Python3✅ | running-sum-of-1d-array | 0 | 1 | # Solutions\n```C++ []\nclass Solution {\npublic:\n vector<int> runningSum(vector<int>& nums) {\n vector<int> answer;\n int running_sum = 0;\n for (int i = 0; i < nums.size(); i++){\n running_sum += nums[i];\n answer.push_back(running_sum);\n }\n return answer;\n }\n};\n```\n```Python3 []\nclass Solution:\n def runningSum(self, nums: List[int]) -> List[int]:\n answer = []\n running_sum = 0\n for i in nums:\n running_sum += i\n answer.append(running_sum)\n return answer\n```\n | 1 | Given an array `nums`. We define a running sum of an array as `runningSum[i] = sum(nums[0]...nums[i])`.
Return the running sum of `nums`.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[1,3,6,10\]
**Explanation:** Running sum is obtained as follows: \[1, 1+2, 1+2+3, 1+2+3+4\].
**Example 2:**
**Input:** nums = \[1,1,1,1,1\]
**Output:** \[1,2,3,4,5\]
**Explanation:** Running sum is obtained as follows: \[1, 1+1, 1+1+1, 1+1+1+1, 1+1+1+1+1\].
**Example 3:**
**Input:** nums = \[3,1,2,10,1\]
**Output:** \[3,4,6,16,17\]
**Constraints:**
* `1 <= nums.length <= 1000`
* `-10^6 <= nums[i] <= 10^6` | null |
Solutions in C++ and Python3✅ | running-sum-of-1d-array | 0 | 1 | # Solutions\n```C++ []\nclass Solution {\npublic:\n vector<int> runningSum(vector<int>& nums) {\n vector<int> answer;\n int running_sum = 0;\n for (int i = 0; i < nums.size(); i++){\n running_sum += nums[i];\n answer.push_back(running_sum);\n }\n return answer;\n }\n};\n```\n```Python3 []\nclass Solution:\n def runningSum(self, nums: List[int]) -> List[int]:\n answer = []\n running_sum = 0\n for i in nums:\n running_sum += i\n answer.append(running_sum)\n return answer\n```\n | 1 | Design a parking system for a parking lot. The parking lot has three kinds of parking spaces: big, medium, and small, with a fixed number of slots for each size.
Implement the `ParkingSystem` class:
* `ParkingSystem(int big, int medium, int small)` Initializes object of the `ParkingSystem` class. The number of slots for each parking space are given as part of the constructor.
* `bool addCar(int carType)` Checks whether there is a parking space of `carType` for the car that wants to get into the parking lot. `carType` can be of three kinds: big, medium, or small, which are represented by `1`, `2`, and `3` respectively. **A car can only park in a parking space of its** `carType`. If there is no space available, return `false`, else park the car in that size space and return `true`.
**Example 1:**
**Input**
\[ "ParkingSystem ", "addCar ", "addCar ", "addCar ", "addCar "\]
\[\[1, 1, 0\], \[1\], \[2\], \[3\], \[1\]\]
**Output**
\[null, true, true, false, false\]
**Explanation**
ParkingSystem parkingSystem = new ParkingSystem(1, 1, 0);
parkingSystem.addCar(1); // return true because there is 1 available slot for a big car
parkingSystem.addCar(2); // return true because there is 1 available slot for a medium car
parkingSystem.addCar(3); // return false because there is no available slot for a small car
parkingSystem.addCar(1); // return false because there is no available slot for a big car. It is already occupied.
**Constraints:**
* `0 <= big, medium, small <= 1000`
* `carType` is `1`, `2`, or `3`
* At most `1000` calls will be made to `addCar` | Think about how we can calculate the i-th number in the running sum from the (i-1)-th number. |
Comprehensive Python Explanation, 4 methods | running-sum-of-1d-array | 0 | 1 | **Intuition**\nTo solve this problem we need to create an array that will store the running sum up to that index. There are many ways to do this, starting from the most basic brute force to a neat single pass.\n\n**Method 1: Pure Brute Force; Time: O(N^2), Space: O(N)**\n```\ndef runningSum(self, nums: List[int]) -> List[int]:\n\tanswer = [] #array to keep track of our answer\n\tfor i in range(len(nums)): #iterate through all the elements in nums\n\t\trunningSum = 0 #this will keep track of the running sum up to index i\n\t\tfor j in range(i+1): \n\t\t\trunningSum += nums[j] #sum all the elements leading up to nums[i]\n\t\tanswer.append(runningSum) #add the sum to our answer array\n\treturn answer\n```\nThe idea behind this method is that for every index i in nums, we will iterate from 0 to i and sum the elements in nums to get the running sum. The time complexity is O(N^2) since we need to iterate up to index i for every value of i between 0 and N. The space complexity is O(N) since our answer array has length N (where N is the length of nums).\n\n **Method 2: Brute Force with List Comprehension; Time: O(N^2), Space: O(N)**\n ```\n def runningSum(self, nums: List[int]) -> List[int]:\n\treturn [sum(nums[:i+1]) for i in range(len(nums))]\n```\nThis method works the same as Method 1 but is a neat one liner. ```sum(nums[:i+1])``` performs the same function as our nested for loop in method 1, finding the running sum up to that point. \n\n**Improving from Brute Force**\nBoth of these methods are accepted, but when we find a working solution, we should always ask if we can think of a better one. In this case, there is a way to complete the function in one pass, lowering the time complexity from O(N^2) to O(N).\n\n**Method 3: One Pass; Time: O(N), Space: O(N)**\n```\ndef runningSum(self, nums: List[int]) -> List[int]:\n\trunSum = [nums[0]] #our answer array starts with nums[0], which is the 0th running sum\n\tfor i in range(1,len(nums)):\n\t\trunSum.append(runSum[i-1]+nums[i]) #the running sum up to index i is the sum of nums[i] and the running sum up to index i-1\n\treturn runSum\n```\nThe key insight here is that the running sum up to index i is the sum of nums[i] and the running sum up to index i-1. Here is a more detailled explanation:\nWe know that ```runningSum[i] = nums[0] + nums[1] + ... + nums[i-1] + nums[i]```. \nHowever, ```runningSum[i-1] = nums[0] + nums[1] + ... + nums[i-1]```, so we can rewrite the first expression to get that ```runningSum[i] = runningSum[i-1] + nums[i]```!\n\nThis code has a time complexity of O(N) since it only takes one pass, which will make the program run much faster when given a very large nums array. However, there is still a way to optimize the space we use.\n\n**Method 4: One Pass, In-Place Solution; Time: O(N), Space: O(1)**\n```\ndef runningSum(self, nums: List[int]) -> List[int]:\n\tfor i in range(1,len(nums)):\n\t\tnums[i] = nums[i-1] + nums[i]\n\treturn nums\n```\nThis method uses the same insight as Method 3 but does it without using an extra array to store the result!. If we are currently at index i, we can assume ```nums[i-1], nums[i-2]... nums[0]``` have all been visited before and therefore contain the running sum up to that point. This means that ```nums[i-1]``` is actually the same as ```runSum[i-1]``` in the last method! By modifying nums in-place and not using an extra array, we cut down on any unnecessary extra space.\n\n\n**Thanks for Reading!**\nIf this post has been helpful please consider upvoting! Also, if I made any mistakes or there are other optimizations, methods I didn\'t consider, etc. please let me know!\n\n\n | 270 | Given an array `nums`. We define a running sum of an array as `runningSum[i] = sum(nums[0]...nums[i])`.
Return the running sum of `nums`.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[1,3,6,10\]
**Explanation:** Running sum is obtained as follows: \[1, 1+2, 1+2+3, 1+2+3+4\].
**Example 2:**
**Input:** nums = \[1,1,1,1,1\]
**Output:** \[1,2,3,4,5\]
**Explanation:** Running sum is obtained as follows: \[1, 1+1, 1+1+1, 1+1+1+1, 1+1+1+1+1\].
**Example 3:**
**Input:** nums = \[3,1,2,10,1\]
**Output:** \[3,4,6,16,17\]
**Constraints:**
* `1 <= nums.length <= 1000`
* `-10^6 <= nums[i] <= 10^6` | null |
Comprehensive Python Explanation, 4 methods | running-sum-of-1d-array | 0 | 1 | **Intuition**\nTo solve this problem we need to create an array that will store the running sum up to that index. There are many ways to do this, starting from the most basic brute force to a neat single pass.\n\n**Method 1: Pure Brute Force; Time: O(N^2), Space: O(N)**\n```\ndef runningSum(self, nums: List[int]) -> List[int]:\n\tanswer = [] #array to keep track of our answer\n\tfor i in range(len(nums)): #iterate through all the elements in nums\n\t\trunningSum = 0 #this will keep track of the running sum up to index i\n\t\tfor j in range(i+1): \n\t\t\trunningSum += nums[j] #sum all the elements leading up to nums[i]\n\t\tanswer.append(runningSum) #add the sum to our answer array\n\treturn answer\n```\nThe idea behind this method is that for every index i in nums, we will iterate from 0 to i and sum the elements in nums to get the running sum. The time complexity is O(N^2) since we need to iterate up to index i for every value of i between 0 and N. The space complexity is O(N) since our answer array has length N (where N is the length of nums).\n\n **Method 2: Brute Force with List Comprehension; Time: O(N^2), Space: O(N)**\n ```\n def runningSum(self, nums: List[int]) -> List[int]:\n\treturn [sum(nums[:i+1]) for i in range(len(nums))]\n```\nThis method works the same as Method 1 but is a neat one liner. ```sum(nums[:i+1])``` performs the same function as our nested for loop in method 1, finding the running sum up to that point. \n\n**Improving from Brute Force**\nBoth of these methods are accepted, but when we find a working solution, we should always ask if we can think of a better one. In this case, there is a way to complete the function in one pass, lowering the time complexity from O(N^2) to O(N).\n\n**Method 3: One Pass; Time: O(N), Space: O(N)**\n```\ndef runningSum(self, nums: List[int]) -> List[int]:\n\trunSum = [nums[0]] #our answer array starts with nums[0], which is the 0th running sum\n\tfor i in range(1,len(nums)):\n\t\trunSum.append(runSum[i-1]+nums[i]) #the running sum up to index i is the sum of nums[i] and the running sum up to index i-1\n\treturn runSum\n```\nThe key insight here is that the running sum up to index i is the sum of nums[i] and the running sum up to index i-1. Here is a more detailled explanation:\nWe know that ```runningSum[i] = nums[0] + nums[1] + ... + nums[i-1] + nums[i]```. \nHowever, ```runningSum[i-1] = nums[0] + nums[1] + ... + nums[i-1]```, so we can rewrite the first expression to get that ```runningSum[i] = runningSum[i-1] + nums[i]```!\n\nThis code has a time complexity of O(N) since it only takes one pass, which will make the program run much faster when given a very large nums array. However, there is still a way to optimize the space we use.\n\n**Method 4: One Pass, In-Place Solution; Time: O(N), Space: O(1)**\n```\ndef runningSum(self, nums: List[int]) -> List[int]:\n\tfor i in range(1,len(nums)):\n\t\tnums[i] = nums[i-1] + nums[i]\n\treturn nums\n```\nThis method uses the same insight as Method 3 but does it without using an extra array to store the result!. If we are currently at index i, we can assume ```nums[i-1], nums[i-2]... nums[0]``` have all been visited before and therefore contain the running sum up to that point. This means that ```nums[i-1]``` is actually the same as ```runSum[i-1]``` in the last method! By modifying nums in-place and not using an extra array, we cut down on any unnecessary extra space.\n\n\n**Thanks for Reading!**\nIf this post has been helpful please consider upvoting! Also, if I made any mistakes or there are other optimizations, methods I didn\'t consider, etc. please let me know!\n\n\n | 270 | Design a parking system for a parking lot. The parking lot has three kinds of parking spaces: big, medium, and small, with a fixed number of slots for each size.
Implement the `ParkingSystem` class:
* `ParkingSystem(int big, int medium, int small)` Initializes object of the `ParkingSystem` class. The number of slots for each parking space are given as part of the constructor.
* `bool addCar(int carType)` Checks whether there is a parking space of `carType` for the car that wants to get into the parking lot. `carType` can be of three kinds: big, medium, or small, which are represented by `1`, `2`, and `3` respectively. **A car can only park in a parking space of its** `carType`. If there is no space available, return `false`, else park the car in that size space and return `true`.
**Example 1:**
**Input**
\[ "ParkingSystem ", "addCar ", "addCar ", "addCar ", "addCar "\]
\[\[1, 1, 0\], \[1\], \[2\], \[3\], \[1\]\]
**Output**
\[null, true, true, false, false\]
**Explanation**
ParkingSystem parkingSystem = new ParkingSystem(1, 1, 0);
parkingSystem.addCar(1); // return true because there is 1 available slot for a big car
parkingSystem.addCar(2); // return true because there is 1 available slot for a medium car
parkingSystem.addCar(3); // return false because there is no available slot for a small car
parkingSystem.addCar(1); // return false because there is no available slot for a big car. It is already occupied.
**Constraints:**
* `0 <= big, medium, small <= 1000`
* `carType` is `1`, `2`, or `3`
* At most `1000` calls will be made to `addCar` | Think about how we can calculate the i-th number in the running sum from the (i-1)-th number. |
Very Easy || 0 ms || 100% || Fully Explained || Java, C++, Python, JS, Python3 | running-sum-of-1d-array | 1 | 1 | # **Java Solution:**\n```\n// Runtime: 0 ms, faster than 100.00% of Java online submissions for Running Sum of 1d Array.\n// Time Complexity : O(n)\n// Space Complexity : O(n)\nclass Solution {\n public int[] runningSum(int[] nums) {\n // Create an output array of size equal to given nums size...\n int[] output = new int[nums.length];\n // Base case: if the array is empty...\n if(nums.length == 0)\n return output;\n // Set output[0] = nums[0]...\n output[0] = nums[0];\n // Traverse all elements through the for loop...\n for(int idx = 1; idx < nums.length; idx++) {\n // Storing the running sum...\n output[idx] = output[idx-1]+ nums[idx];\n }\n return output; // Return the running sum of nums...\n }\n}\n```\n\n# **C++ Solution:**\n```\n// Time Complexity : O(n)\n// Space Complexity : O(n)\nclass Solution {\npublic:\n vector<int> runningSum(vector<int>& nums) {\n // Create an output array of size equal to given nums size...\n vector<int> output(nums.size());\n // Base case: if the array is empty...\n if(nums.size() == 0)\n return output;\n // Set output[0] = nums[0]...\n output[0] = nums[0];\n // Traverse all elements through the for loop...\n for(int idx = 1; idx < nums.size(); idx++) {\n // Storing the running sum...\n output[idx] = output[idx-1] + nums[idx];\n } return output; // Return the running sum of nums...\n }\n};\n```\n\n# **Python/Python3 Solution:**\n```\n# Time Complexity : O(n)\n# Space Complexity : O(n)\nclass Solution(object):\n def runningSum(self, nums):\n # Create an output array of size equal to given nums size...\n output = [0] * len(nums)\n # Set output[0] = nums[0]...\n output[0] = nums[0]\n # Traverse all elements through the for loop...\n for idx in range(1, len(nums)):\n # Storing the running sum...\n output[idx] = output[idx - 1] + nums[idx]\n return output # Return the running sum of nums...\n```\n \n# **JavaScript Solution:**\n```\n// Time Complexity : O(n)\n// Space Complexity : O(n)\nvar runningSum = function(nums) {\n // Create an output array of size equal to given nums size...\n let output = new Array(nums.length)\n // Set output[0] = nums[0]...\n output[0] = nums[0];\n // Traverse all elements through the for loop...\n for(let idx = 1; idx < nums.length; idx++) {\n // Storing the running sum...\n output[idx] = output[idx-1] + nums[idx];\n }\n return output; // Return the running sum of nums...\n};\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 183 | Given an array `nums`. We define a running sum of an array as `runningSum[i] = sum(nums[0]...nums[i])`.
Return the running sum of `nums`.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[1,3,6,10\]
**Explanation:** Running sum is obtained as follows: \[1, 1+2, 1+2+3, 1+2+3+4\].
**Example 2:**
**Input:** nums = \[1,1,1,1,1\]
**Output:** \[1,2,3,4,5\]
**Explanation:** Running sum is obtained as follows: \[1, 1+1, 1+1+1, 1+1+1+1, 1+1+1+1+1\].
**Example 3:**
**Input:** nums = \[3,1,2,10,1\]
**Output:** \[3,4,6,16,17\]
**Constraints:**
* `1 <= nums.length <= 1000`
* `-10^6 <= nums[i] <= 10^6` | null |
Very Easy || 0 ms || 100% || Fully Explained || Java, C++, Python, JS, Python3 | running-sum-of-1d-array | 1 | 1 | # **Java Solution:**\n```\n// Runtime: 0 ms, faster than 100.00% of Java online submissions for Running Sum of 1d Array.\n// Time Complexity : O(n)\n// Space Complexity : O(n)\nclass Solution {\n public int[] runningSum(int[] nums) {\n // Create an output array of size equal to given nums size...\n int[] output = new int[nums.length];\n // Base case: if the array is empty...\n if(nums.length == 0)\n return output;\n // Set output[0] = nums[0]...\n output[0] = nums[0];\n // Traverse all elements through the for loop...\n for(int idx = 1; idx < nums.length; idx++) {\n // Storing the running sum...\n output[idx] = output[idx-1]+ nums[idx];\n }\n return output; // Return the running sum of nums...\n }\n}\n```\n\n# **C++ Solution:**\n```\n// Time Complexity : O(n)\n// Space Complexity : O(n)\nclass Solution {\npublic:\n vector<int> runningSum(vector<int>& nums) {\n // Create an output array of size equal to given nums size...\n vector<int> output(nums.size());\n // Base case: if the array is empty...\n if(nums.size() == 0)\n return output;\n // Set output[0] = nums[0]...\n output[0] = nums[0];\n // Traverse all elements through the for loop...\n for(int idx = 1; idx < nums.size(); idx++) {\n // Storing the running sum...\n output[idx] = output[idx-1] + nums[idx];\n } return output; // Return the running sum of nums...\n }\n};\n```\n\n# **Python/Python3 Solution:**\n```\n# Time Complexity : O(n)\n# Space Complexity : O(n)\nclass Solution(object):\n def runningSum(self, nums):\n # Create an output array of size equal to given nums size...\n output = [0] * len(nums)\n # Set output[0] = nums[0]...\n output[0] = nums[0]\n # Traverse all elements through the for loop...\n for idx in range(1, len(nums)):\n # Storing the running sum...\n output[idx] = output[idx - 1] + nums[idx]\n return output # Return the running sum of nums...\n```\n \n# **JavaScript Solution:**\n```\n// Time Complexity : O(n)\n// Space Complexity : O(n)\nvar runningSum = function(nums) {\n // Create an output array of size equal to given nums size...\n let output = new Array(nums.length)\n // Set output[0] = nums[0]...\n output[0] = nums[0];\n // Traverse all elements through the for loop...\n for(let idx = 1; idx < nums.length; idx++) {\n // Storing the running sum...\n output[idx] = output[idx-1] + nums[idx];\n }\n return output; // Return the running sum of nums...\n};\n```\n**I am working hard for you guys...\nPlease upvote if you found any help with this code...** | 183 | Design a parking system for a parking lot. The parking lot has three kinds of parking spaces: big, medium, and small, with a fixed number of slots for each size.
Implement the `ParkingSystem` class:
* `ParkingSystem(int big, int medium, int small)` Initializes object of the `ParkingSystem` class. The number of slots for each parking space are given as part of the constructor.
* `bool addCar(int carType)` Checks whether there is a parking space of `carType` for the car that wants to get into the parking lot. `carType` can be of three kinds: big, medium, or small, which are represented by `1`, `2`, and `3` respectively. **A car can only park in a parking space of its** `carType`. If there is no space available, return `false`, else park the car in that size space and return `true`.
**Example 1:**
**Input**
\[ "ParkingSystem ", "addCar ", "addCar ", "addCar ", "addCar "\]
\[\[1, 1, 0\], \[1\], \[2\], \[3\], \[1\]\]
**Output**
\[null, true, true, false, false\]
**Explanation**
ParkingSystem parkingSystem = new ParkingSystem(1, 1, 0);
parkingSystem.addCar(1); // return true because there is 1 available slot for a big car
parkingSystem.addCar(2); // return true because there is 1 available slot for a medium car
parkingSystem.addCar(3); // return false because there is no available slot for a small car
parkingSystem.addCar(1); // return false because there is no available slot for a big car. It is already occupied.
**Constraints:**
* `0 <= big, medium, small <= 1000`
* `carType` is `1`, `2`, or `3`
* At most `1000` calls will be made to `addCar` | Think about how we can calculate the i-th number in the running sum from the (i-1)-th number. |
Simple Python Approach | running-sum-of-1d-array | 0 | 1 | # Code\n```\nclass Solution:\n def runningSum(self, nums: List[int]) -> List[int]:\n # The variable that will have the running sum\n tot = 0\n # The array that will hold the running su,\n ans = []\n # For loop\n for ele in nums:\n # Adding the element\n tot += ele\n # Appending this running sum to ans\n ans.append(tot)\n # Return ans\n return ans\n``` | 8 | Given an array `nums`. We define a running sum of an array as `runningSum[i] = sum(nums[0]...nums[i])`.
Return the running sum of `nums`.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[1,3,6,10\]
**Explanation:** Running sum is obtained as follows: \[1, 1+2, 1+2+3, 1+2+3+4\].
**Example 2:**
**Input:** nums = \[1,1,1,1,1\]
**Output:** \[1,2,3,4,5\]
**Explanation:** Running sum is obtained as follows: \[1, 1+1, 1+1+1, 1+1+1+1, 1+1+1+1+1\].
**Example 3:**
**Input:** nums = \[3,1,2,10,1\]
**Output:** \[3,4,6,16,17\]
**Constraints:**
* `1 <= nums.length <= 1000`
* `-10^6 <= nums[i] <= 10^6` | null |
Simple Python Approach | running-sum-of-1d-array | 0 | 1 | # Code\n```\nclass Solution:\n def runningSum(self, nums: List[int]) -> List[int]:\n # The variable that will have the running sum\n tot = 0\n # The array that will hold the running su,\n ans = []\n # For loop\n for ele in nums:\n # Adding the element\n tot += ele\n # Appending this running sum to ans\n ans.append(tot)\n # Return ans\n return ans\n``` | 8 | Design a parking system for a parking lot. The parking lot has three kinds of parking spaces: big, medium, and small, with a fixed number of slots for each size.
Implement the `ParkingSystem` class:
* `ParkingSystem(int big, int medium, int small)` Initializes object of the `ParkingSystem` class. The number of slots for each parking space are given as part of the constructor.
* `bool addCar(int carType)` Checks whether there is a parking space of `carType` for the car that wants to get into the parking lot. `carType` can be of three kinds: big, medium, or small, which are represented by `1`, `2`, and `3` respectively. **A car can only park in a parking space of its** `carType`. If there is no space available, return `false`, else park the car in that size space and return `true`.
**Example 1:**
**Input**
\[ "ParkingSystem ", "addCar ", "addCar ", "addCar ", "addCar "\]
\[\[1, 1, 0\], \[1\], \[2\], \[3\], \[1\]\]
**Output**
\[null, true, true, false, false\]
**Explanation**
ParkingSystem parkingSystem = new ParkingSystem(1, 1, 0);
parkingSystem.addCar(1); // return true because there is 1 available slot for a big car
parkingSystem.addCar(2); // return true because there is 1 available slot for a medium car
parkingSystem.addCar(3); // return false because there is no available slot for a small car
parkingSystem.addCar(1); // return false because there is no available slot for a big car. It is already occupied.
**Constraints:**
* `0 <= big, medium, small <= 1000`
* `carType` is `1`, `2`, or `3`
* At most `1000` calls will be made to `addCar` | Think about how we can calculate the i-th number in the running sum from the (i-1)-th number. |
[Java/Python 3] Greedy Alg.: 3 methods from O(nlogn) to O(n) w/ brief explanation and analysis. | least-number-of-unique-integers-after-k-removals | 1 | 1 | **[Summary]**\nRemove k least frequent elements to make the remaining ones as least unique ints set.\n\n----\n**Method 1: HashMap and PriorityQueue** -- credit to **@usamaten** and **@sparker123**.\nCount number then put the frequencies into a PriorityQueue/heap:\n\n```java\n public int findLeastNumOfUniqueInts(int[] arr, int k) {\n Map<Integer, Integer> count = new HashMap<>();\n for (int a : arr)\n count.put(a, 1 + count.getOrDefault(a, 0));\n PriorityQueue<Integer> pq = new PriorityQueue<>(count.values());\n while (k > 0)\n k -= pq.poll();\n return k < 0 ? pq.size() + 1 : pq.size(); \n }\n```\n```python\n def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n hp = list(collections.Counter(arr).values())\n heapq.heapify(hp)\n while k > 0:\n k -= heapq.heappop(hp)\n return len(hp) + (k < 0) \n```\n**Analysis:**\n`new PriorityQueue<>(count.values());` and `for` loop both cost `O(n)` in worst case, the `while` loop cost `O(klogn)` time. Therefore,\n\nTime: `O(n + klogn)`, space: `O(n)`.\n\n----\n\n**Method 2: HashMap and TreeMap**\nCount number then count occurrence:\n\n1. Count the occurrences of each number using HashMap;\n2. Using TreeMap to count each occurrence;\n3. Poll out currently least frequent elemnets, and check if reaching `k`, deduct the correponding unique count `remaining`.\n\n```java\n public int findLeastNumOfUniqueInts(int[] arr, int k) {\n Map<Integer, Integer> count = new HashMap<>();\n for (int a : arr)\n count.put(a, 1 + count.getOrDefault(a, 0));\n int remaining = count.size();\n TreeMap<Integer, Integer> occurrenceCount = new TreeMap<>();\n for (int v : count.values())\n occurrenceCount.put(v, 1 + occurrenceCount.getOrDefault(v, 0));\n while (k > 0) {\n Map.Entry<Integer, Integer> entry = occurrenceCount.pollFirstEntry();\n if (k - entry.getKey() * entry.getValue() >= 0) {\n k -= entry.getKey() * entry.getValue();\n remaining -= entry.getValue();\n }else {\n return remaining - k / entry.getKey();\n }\n }\n return remaining; \n }\n```\n```python\n def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n c = Counter(arr)\n cnt, remaining = Counter(c.values()), len(c)\n for key in sorted(cnt): \n if k >= key * cnt[key]:\n k -= key * cnt[key]\n remaining -= cnt.pop(key)\n else:\n return remaining - k // key\n return remaining\n```\n**Analysis:**\nTime: `O(nlogn)`, space: `O(n)`.\n\n----\n\n**Method 3: HashMap and Array** -- credit to **@krrs**.\nCount number then count occurrence:\n\n1. Count the occurrences of each number using HashMap;\n2. Using Array to count each occurrence, since max occurrence <= `arr.length`;\n3. From small to big, for each unvisited least frequent element, deduct from `k` the multiplication with the number of elements of same occurrence, check if reaching `0`, then deduct the correponding unique count `remaining`.\n\n```java\n public int findLeastNumOfUniqueInts(int[] arr, int k) {\n Map<Integer, Integer> count = new HashMap<>();\n for (int a : arr)\n count.put(a, 1 + count.getOrDefault(a, 0));\n int remaining = count.size(), occur = 1;\n int[] occurrenceCount = new int[arr.length + 1];\n for (int v : count.values())\n ++occurrenceCount[v];\n while (k > 0) {\n if (k - occur * occurrenceCount[occur] >= 0) {\n k -= occur * occurrenceCount[occur];\n remaining -= occurrenceCount[occur++];\n }else {\n return remaining - k / occur;\n }\n }\n return remaining; \n }\n```\n\n**Q & A:**\n\nQ1: Why do we need `occur * occurrenceCount[occur]` instead of just `occurrenceCount[occur]` in Java code?\nA1: E.g., both `5` and `8` appear `6` times; We use a `HashMap/dict` to save them as `{5:6, 8:6}`; then we count the `6` in `values()` frequency as `occurrenceCount[6] = 2`, now `occur` in my code corresponds to `6` and the frequency of `6`, `2`, corresponds to `occurrenceCount[occur]`.\n\nTherefore, there are `2` numbers occur `6` times, which is `occurrenceCount[occur] * occur = 2 * 6 = 12` times. \n\nQ2: How u got this formula remaining - k // key in Python 3 code?\nA2: `key` indicates the occurrence of elements in input array, and `cnt[key]` indicates the frequency of the occurrence. If `k < key * cnt[key]`, it implies we can NOT remove all elements with the occurrence of `key`. Therefore, we can at most remove part of them. \n\n E.g., both `5` and `8` appear `6` times; We use a `HashMap/dict` to save them as `{5:6, 8:6}`; then we count the `6` in `values()` occurrence as `cnt[6] = 2`, now `key` in my code corresponds to `6` and the frequency of `6`, `2`, corresponds to `cnt[key]`.\n \n Now if `k = 10 < 12 = 6 * 2 = key * cnt[key]`, we can only remove `k // key = 10 / 6 = 1` unique element.\n \n**End of Q & A**\n\n----\n\n```python\n def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n c = Counter(arr)\n cnt, remaining = Counter(c.values()), len(c)\n for key in range(1, len(arr) + 1): \n if k >= key * cnt[key]:\n k -= key * cnt[key]\n remaining -= cnt[key]\n else:\n return remaining - k // key\n return remaining\n```\n**Analysis:**\nTime: `O(n)`, space: `O(n)`.\n\n----\n\nPlease let me know if you have any confusion or questions, and please **upvote** if the post is helpful. | 170 | Given an array of integers `arr` and an integer `k`. Find the _least number of unique integers_ after removing **exactly** `k` elements**.**
**Example 1:**
**Input:** arr = \[5,5,4\], k = 1
**Output:** 1
**Explanation**: Remove the single 4, only 5 is left.
**Example 2:**
**Input:** arr = \[4,3,1,1,3,3,2\], k = 3
**Output:** 2
**Explanation**: Remove 4, 2 and either one of the two 1s or three 3s. 1 and 3 will be left.
**Constraints:**
* `1 <= arr.length <= 10^5`
* `1 <= arr[i] <= 10^9`
* `0 <= k <= arr.length` | null |
[Java/Python 3] Greedy Alg.: 3 methods from O(nlogn) to O(n) w/ brief explanation and analysis. | least-number-of-unique-integers-after-k-removals | 1 | 1 | **[Summary]**\nRemove k least frequent elements to make the remaining ones as least unique ints set.\n\n----\n**Method 1: HashMap and PriorityQueue** -- credit to **@usamaten** and **@sparker123**.\nCount number then put the frequencies into a PriorityQueue/heap:\n\n```java\n public int findLeastNumOfUniqueInts(int[] arr, int k) {\n Map<Integer, Integer> count = new HashMap<>();\n for (int a : arr)\n count.put(a, 1 + count.getOrDefault(a, 0));\n PriorityQueue<Integer> pq = new PriorityQueue<>(count.values());\n while (k > 0)\n k -= pq.poll();\n return k < 0 ? pq.size() + 1 : pq.size(); \n }\n```\n```python\n def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n hp = list(collections.Counter(arr).values())\n heapq.heapify(hp)\n while k > 0:\n k -= heapq.heappop(hp)\n return len(hp) + (k < 0) \n```\n**Analysis:**\n`new PriorityQueue<>(count.values());` and `for` loop both cost `O(n)` in worst case, the `while` loop cost `O(klogn)` time. Therefore,\n\nTime: `O(n + klogn)`, space: `O(n)`.\n\n----\n\n**Method 2: HashMap and TreeMap**\nCount number then count occurrence:\n\n1. Count the occurrences of each number using HashMap;\n2. Using TreeMap to count each occurrence;\n3. Poll out currently least frequent elemnets, and check if reaching `k`, deduct the correponding unique count `remaining`.\n\n```java\n public int findLeastNumOfUniqueInts(int[] arr, int k) {\n Map<Integer, Integer> count = new HashMap<>();\n for (int a : arr)\n count.put(a, 1 + count.getOrDefault(a, 0));\n int remaining = count.size();\n TreeMap<Integer, Integer> occurrenceCount = new TreeMap<>();\n for (int v : count.values())\n occurrenceCount.put(v, 1 + occurrenceCount.getOrDefault(v, 0));\n while (k > 0) {\n Map.Entry<Integer, Integer> entry = occurrenceCount.pollFirstEntry();\n if (k - entry.getKey() * entry.getValue() >= 0) {\n k -= entry.getKey() * entry.getValue();\n remaining -= entry.getValue();\n }else {\n return remaining - k / entry.getKey();\n }\n }\n return remaining; \n }\n```\n```python\n def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n c = Counter(arr)\n cnt, remaining = Counter(c.values()), len(c)\n for key in sorted(cnt): \n if k >= key * cnt[key]:\n k -= key * cnt[key]\n remaining -= cnt.pop(key)\n else:\n return remaining - k // key\n return remaining\n```\n**Analysis:**\nTime: `O(nlogn)`, space: `O(n)`.\n\n----\n\n**Method 3: HashMap and Array** -- credit to **@krrs**.\nCount number then count occurrence:\n\n1. Count the occurrences of each number using HashMap;\n2. Using Array to count each occurrence, since max occurrence <= `arr.length`;\n3. From small to big, for each unvisited least frequent element, deduct from `k` the multiplication with the number of elements of same occurrence, check if reaching `0`, then deduct the correponding unique count `remaining`.\n\n```java\n public int findLeastNumOfUniqueInts(int[] arr, int k) {\n Map<Integer, Integer> count = new HashMap<>();\n for (int a : arr)\n count.put(a, 1 + count.getOrDefault(a, 0));\n int remaining = count.size(), occur = 1;\n int[] occurrenceCount = new int[arr.length + 1];\n for (int v : count.values())\n ++occurrenceCount[v];\n while (k > 0) {\n if (k - occur * occurrenceCount[occur] >= 0) {\n k -= occur * occurrenceCount[occur];\n remaining -= occurrenceCount[occur++];\n }else {\n return remaining - k / occur;\n }\n }\n return remaining; \n }\n```\n\n**Q & A:**\n\nQ1: Why do we need `occur * occurrenceCount[occur]` instead of just `occurrenceCount[occur]` in Java code?\nA1: E.g., both `5` and `8` appear `6` times; We use a `HashMap/dict` to save them as `{5:6, 8:6}`; then we count the `6` in `values()` frequency as `occurrenceCount[6] = 2`, now `occur` in my code corresponds to `6` and the frequency of `6`, `2`, corresponds to `occurrenceCount[occur]`.\n\nTherefore, there are `2` numbers occur `6` times, which is `occurrenceCount[occur] * occur = 2 * 6 = 12` times. \n\nQ2: How u got this formula remaining - k // key in Python 3 code?\nA2: `key` indicates the occurrence of elements in input array, and `cnt[key]` indicates the frequency of the occurrence. If `k < key * cnt[key]`, it implies we can NOT remove all elements with the occurrence of `key`. Therefore, we can at most remove part of them. \n\n E.g., both `5` and `8` appear `6` times; We use a `HashMap/dict` to save them as `{5:6, 8:6}`; then we count the `6` in `values()` occurrence as `cnt[6] = 2`, now `key` in my code corresponds to `6` and the frequency of `6`, `2`, corresponds to `cnt[key]`.\n \n Now if `k = 10 < 12 = 6 * 2 = key * cnt[key]`, we can only remove `k // key = 10 / 6 = 1` unique element.\n \n**End of Q & A**\n\n----\n\n```python\n def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n c = Counter(arr)\n cnt, remaining = Counter(c.values()), len(c)\n for key in range(1, len(arr) + 1): \n if k >= key * cnt[key]:\n k -= key * cnt[key]\n remaining -= cnt[key]\n else:\n return remaining - k // key\n return remaining\n```\n**Analysis:**\nTime: `O(n)`, space: `O(n)`.\n\n----\n\nPlease let me know if you have any confusion or questions, and please **upvote** if the post is helpful. | 170 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
Python || 3 Line || Shortest, Simplest | least-number-of-unique-integers-after-k-removals | 0 | 1 | > Idea is to remove \\"elements which have least count\\" so remaining have least unique char.\n\n\n```\ndef findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n c = Counter(arr)\n s = sorted(arr,key = lambda x:(c[x],x))\n return len(set(s[k:]))\n \n```\nupvote if you find it good.\n> Update - You can check this [Post](https://leetcode.com/problems/count-good-nodes-in-binary-tree/discuss/635351/BFS-With-MaxValue-or-Template-of-Similar-Problems-Python) also. Hope that will be benificial to new leetcoders for that kind of problems. -> [Post](https://leetcode.com/problems/count-good-nodes-in-binary-tree/discuss/635351/BFS-With-MaxValue-or-Template-of-Similar-Problems-Python) | 86 | Given an array of integers `arr` and an integer `k`. Find the _least number of unique integers_ after removing **exactly** `k` elements**.**
**Example 1:**
**Input:** arr = \[5,5,4\], k = 1
**Output:** 1
**Explanation**: Remove the single 4, only 5 is left.
**Example 2:**
**Input:** arr = \[4,3,1,1,3,3,2\], k = 3
**Output:** 2
**Explanation**: Remove 4, 2 and either one of the two 1s or three 3s. 1 and 3 will be left.
**Constraints:**
* `1 <= arr.length <= 10^5`
* `1 <= arr[i] <= 10^9`
* `0 <= k <= arr.length` | null |
Python || 3 Line || Shortest, Simplest | least-number-of-unique-integers-after-k-removals | 0 | 1 | > Idea is to remove \\"elements which have least count\\" so remaining have least unique char.\n\n\n```\ndef findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n c = Counter(arr)\n s = sorted(arr,key = lambda x:(c[x],x))\n return len(set(s[k:]))\n \n```\nupvote if you find it good.\n> Update - You can check this [Post](https://leetcode.com/problems/count-good-nodes-in-binary-tree/discuss/635351/BFS-With-MaxValue-or-Template-of-Similar-Problems-Python) also. Hope that will be benificial to new leetcoders for that kind of problems. -> [Post](https://leetcode.com/problems/count-good-nodes-in-binary-tree/discuss/635351/BFS-With-MaxValue-or-Template-of-Similar-Problems-Python) | 86 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
[Python 3] Counter and commented | least-number-of-unique-integers-after-k-removals | 0 | 1 | ```\nclass Solution:\n def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n # Counter sort the element in the list from most common to least common and return as a dictionary\n counter = collections.Counter(arr)\n # use most_common() to show the first n element, but in this case, n not define, so it will be all the element\n # and return type will be 2d list\n counter = counter.most_common()\n unique = len(counter)\n while k>0 and unique>0:\n # if the value k is enough to remove the least common element\n if k>=counter[-1][1]:\n # remove the needed amount to pop the least common element\n k -= counter[-1][1]\n # pop the last element in the list\n counter.pop()\n # decrement the unique since the last element poped\n unique -= 1\n # if the value k is not enough to remove the least common element\n else:\n return unique\n return unique \n``` | 1 | Given an array of integers `arr` and an integer `k`. Find the _least number of unique integers_ after removing **exactly** `k` elements**.**
**Example 1:**
**Input:** arr = \[5,5,4\], k = 1
**Output:** 1
**Explanation**: Remove the single 4, only 5 is left.
**Example 2:**
**Input:** arr = \[4,3,1,1,3,3,2\], k = 3
**Output:** 2
**Explanation**: Remove 4, 2 and either one of the two 1s or three 3s. 1 and 3 will be left.
**Constraints:**
* `1 <= arr.length <= 10^5`
* `1 <= arr[i] <= 10^9`
* `0 <= k <= arr.length` | null |
[Python 3] Counter and commented | least-number-of-unique-integers-after-k-removals | 0 | 1 | ```\nclass Solution:\n def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n # Counter sort the element in the list from most common to least common and return as a dictionary\n counter = collections.Counter(arr)\n # use most_common() to show the first n element, but in this case, n not define, so it will be all the element\n # and return type will be 2d list\n counter = counter.most_common()\n unique = len(counter)\n while k>0 and unique>0:\n # if the value k is enough to remove the least common element\n if k>=counter[-1][1]:\n # remove the needed amount to pop the least common element\n k -= counter[-1][1]\n # pop the last element in the list\n counter.pop()\n # decrement the unique since the last element poped\n unique -= 1\n # if the value k is not enough to remove the least common element\n else:\n return unique\n return unique \n``` | 1 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
Python 97.55% faster [EXPLAINED] | breakdown | Hash table | least-number-of-unique-integers-after-k-removals | 0 | 1 | # Intuition\r\n- This problem is similar to [majority elements](https://leetcode.com/problems/majority-element/) problem in which we have to delete the digit whose `frequency >= length(array)/2`.\r\n- Similarly in this problem we will delete those elements whose `sum of frequencies >= k`.\r\n\r\n# Approach\r\n- First we will create frequency dictionary.\r\n- Now we will iterate through our dictionary and pick the element whose frequecy is least among all because at the end we want **least** number of **unique** elements.\r\n- **Picking up less frequent unique elements means we have to pick more unique elements, picking more unique elements means less unique elements will be left**.\r\n- Our **count** variable keeps track of how many elements(**unique**) we have picked so far.\r\n- Our **curr_deleted** variable keeps track of how many elements(**not unique**) we have picked so far.\r\n- `if count < k`, means we have to select more elements, continue picking.\r\n- `if count == k`, means we have selected k elements, stop picking.\r\n- `if count > k`, means we have picked more than k elements so we have to leave back `count-k` elements means last picked element will not be counted.\r\n\r\n# Complexity\r\n- Time complexity: O(nlogn)\r\n\r\n- Space complexity: O(n)\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\r\n d = {}\r\n for i in arr:\r\n d[i] = d.get(i, 0)+1\r\n\r\n unique_elements = len(d)\r\n curr_deleted = 0\r\n count = 0\r\n for frequency in sorted(d.values()):\r\n curr_deleted += frequency\r\n count += 1\r\n if curr_deleted < k:\r\n continue\r\n elif curr_deleted == k:\r\n return unique_elements-count\r\n else:\r\n return unique_elements-(count-1)\r\n \r\n```\r\n------------------\r\n**Upvote the post if you find it helpful.\r\nHappy coding.** | 4 | Given an array of integers `arr` and an integer `k`. Find the _least number of unique integers_ after removing **exactly** `k` elements**.**
**Example 1:**
**Input:** arr = \[5,5,4\], k = 1
**Output:** 1
**Explanation**: Remove the single 4, only 5 is left.
**Example 2:**
**Input:** arr = \[4,3,1,1,3,3,2\], k = 3
**Output:** 2
**Explanation**: Remove 4, 2 and either one of the two 1s or three 3s. 1 and 3 will be left.
**Constraints:**
* `1 <= arr.length <= 10^5`
* `1 <= arr[i] <= 10^9`
* `0 <= k <= arr.length` | null |
Python 97.55% faster [EXPLAINED] | breakdown | Hash table | least-number-of-unique-integers-after-k-removals | 0 | 1 | # Intuition\r\n- This problem is similar to [majority elements](https://leetcode.com/problems/majority-element/) problem in which we have to delete the digit whose `frequency >= length(array)/2`.\r\n- Similarly in this problem we will delete those elements whose `sum of frequencies >= k`.\r\n\r\n# Approach\r\n- First we will create frequency dictionary.\r\n- Now we will iterate through our dictionary and pick the element whose frequecy is least among all because at the end we want **least** number of **unique** elements.\r\n- **Picking up less frequent unique elements means we have to pick more unique elements, picking more unique elements means less unique elements will be left**.\r\n- Our **count** variable keeps track of how many elements(**unique**) we have picked so far.\r\n- Our **curr_deleted** variable keeps track of how many elements(**not unique**) we have picked so far.\r\n- `if count < k`, means we have to select more elements, continue picking.\r\n- `if count == k`, means we have selected k elements, stop picking.\r\n- `if count > k`, means we have picked more than k elements so we have to leave back `count-k` elements means last picked element will not be counted.\r\n\r\n# Complexity\r\n- Time complexity: O(nlogn)\r\n\r\n- Space complexity: O(n)\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\r\n d = {}\r\n for i in arr:\r\n d[i] = d.get(i, 0)+1\r\n\r\n unique_elements = len(d)\r\n curr_deleted = 0\r\n count = 0\r\n for frequency in sorted(d.values()):\r\n curr_deleted += frequency\r\n count += 1\r\n if curr_deleted < k:\r\n continue\r\n elif curr_deleted == k:\r\n return unique_elements-count\r\n else:\r\n return unique_elements-(count-1)\r\n \r\n```\r\n------------------\r\n**Upvote the post if you find it helpful.\r\nHappy coding.** | 4 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
94% TC and 65% SC easy python solution | least-number-of-unique-integers-after-k-removals | 0 | 1 | ```\ndef findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n\td = Counter(arr)\n\tans = len(d)\n\td = sorted(d.items(), key = lambda x:x[1])\n\tfor i, j in d:\n\t\tif(j <= k):\n\t\t\tans -= 1\n\t\t\tk -= j\n\t\telse:\n\t\t\tbreak\n\treturn ans\n``` | 3 | Given an array of integers `arr` and an integer `k`. Find the _least number of unique integers_ after removing **exactly** `k` elements**.**
**Example 1:**
**Input:** arr = \[5,5,4\], k = 1
**Output:** 1
**Explanation**: Remove the single 4, only 5 is left.
**Example 2:**
**Input:** arr = \[4,3,1,1,3,3,2\], k = 3
**Output:** 2
**Explanation**: Remove 4, 2 and either one of the two 1s or three 3s. 1 and 3 will be left.
**Constraints:**
* `1 <= arr.length <= 10^5`
* `1 <= arr[i] <= 10^9`
* `0 <= k <= arr.length` | null |
94% TC and 65% SC easy python solution | least-number-of-unique-integers-after-k-removals | 0 | 1 | ```\ndef findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n\td = Counter(arr)\n\tans = len(d)\n\td = sorted(d.items(), key = lambda x:x[1])\n\tfor i, j in d:\n\t\tif(j <= k):\n\t\t\tans -= 1\n\t\t\tk -= j\n\t\telse:\n\t\t\tbreak\n\treturn ans\n``` | 3 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
Faster than 96% 🥇 | least-number-of-unique-integers-after-k-removals | 0 | 1 | ```class Solution:\n def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n d={}\n for i in arr:\n if i not in d:\n d[i]=0\n d[i]+=1\n l=list(d.values())\n l.sort()\n for i in range(len(l)):\n if l[i]<=k:\n k-=l[i]\n l[i]=-1\n else:\n break\n co=0\n for i in l:\n if i!=-1:\n co+=1\n return co | 6 | Given an array of integers `arr` and an integer `k`. Find the _least number of unique integers_ after removing **exactly** `k` elements**.**
**Example 1:**
**Input:** arr = \[5,5,4\], k = 1
**Output:** 1
**Explanation**: Remove the single 4, only 5 is left.
**Example 2:**
**Input:** arr = \[4,3,1,1,3,3,2\], k = 3
**Output:** 2
**Explanation**: Remove 4, 2 and either one of the two 1s or three 3s. 1 and 3 will be left.
**Constraints:**
* `1 <= arr.length <= 10^5`
* `1 <= arr[i] <= 10^9`
* `0 <= k <= arr.length` | null |
Faster than 96% 🥇 | least-number-of-unique-integers-after-k-removals | 0 | 1 | ```class Solution:\n def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n d={}\n for i in arr:\n if i not in d:\n d[i]=0\n d[i]+=1\n l=list(d.values())\n l.sort()\n for i in range(len(l)):\n if l[i]<=k:\n k-=l[i]\n l[i]=-1\n else:\n break\n co=0\n for i in l:\n if i!=-1:\n co+=1\n return co | 6 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
Beats 99% runtime || 98% memory || python || easy | least-number-of-unique-integers-after-k-removals | 0 | 1 | ```\nclass Solution:\n def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n\n count = Counter(arr)\n ans = len(count)\n for i in sorted(count.values()):\n k -= i\n if k < 0:\n break\n ans -= 1\n return ans\n```\n\n**if you find it helpful kindly upvote .** | 18 | Given an array of integers `arr` and an integer `k`. Find the _least number of unique integers_ after removing **exactly** `k` elements**.**
**Example 1:**
**Input:** arr = \[5,5,4\], k = 1
**Output:** 1
**Explanation**: Remove the single 4, only 5 is left.
**Example 2:**
**Input:** arr = \[4,3,1,1,3,3,2\], k = 3
**Output:** 2
**Explanation**: Remove 4, 2 and either one of the two 1s or three 3s. 1 and 3 will be left.
**Constraints:**
* `1 <= arr.length <= 10^5`
* `1 <= arr[i] <= 10^9`
* `0 <= k <= arr.length` | null |
Beats 99% runtime || 98% memory || python || easy | least-number-of-unique-integers-after-k-removals | 0 | 1 | ```\nclass Solution:\n def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n\n count = Counter(arr)\n ans = len(count)\n for i in sorted(count.values()):\n k -= i\n if k < 0:\n break\n ans -= 1\n return ans\n```\n\n**if you find it helpful kindly upvote .** | 18 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
Simple O(n) Python | least-number-of-unique-integers-after-k-removals | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nCounter the occurence then go over the values in ascending order.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- O(n)\n- Space complexity:\n- O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n dic = {}\n for a in arr:\n if a in dic.keys():\n dic[a]+=1\n else: dic[a]=1\n l = sorted(list(dic.values()))\n while k>0:\n k = k - l[0]\n l.pop(0)\n if k==0: return len(l)\n else: return len(l)+1\n\n``` | 0 | Given an array of integers `arr` and an integer `k`. Find the _least number of unique integers_ after removing **exactly** `k` elements**.**
**Example 1:**
**Input:** arr = \[5,5,4\], k = 1
**Output:** 1
**Explanation**: Remove the single 4, only 5 is left.
**Example 2:**
**Input:** arr = \[4,3,1,1,3,3,2\], k = 3
**Output:** 2
**Explanation**: Remove 4, 2 and either one of the two 1s or three 3s. 1 and 3 will be left.
**Constraints:**
* `1 <= arr.length <= 10^5`
* `1 <= arr[i] <= 10^9`
* `0 <= k <= arr.length` | null |
Simple O(n) Python | least-number-of-unique-integers-after-k-removals | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nCounter the occurence then go over the values in ascending order.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- O(n)\n- Space complexity:\n- O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:\n dic = {}\n for a in arr:\n if a in dic.keys():\n dic[a]+=1\n else: dic[a]=1\n l = sorted(list(dic.values()))\n while k>0:\n k = k - l[0]\n l.pop(0)\n if k==0: return len(l)\n else: return len(l)+1\n\n``` | 0 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
🔥[Python 3] Binary search, beats 95% 🥷🏼 | minimum-number-of-days-to-make-m-bouquets | 0 | 1 | ```python3 []\nclass Solution:\n def minDays(self, bloomDay: List[int], m: int, k: int) -> int:\n if len(bloomDay) < m * k: return -1\n\n def isEnoughDays(days):\n flowers, bouquets = 0, 0\n for d in bloomDay:\n flowers = flowers + 1 if d <= days else 0\n if flowers == k:\n bouquets += 1\n if bouquets == m: break\n flowers = 0\n \n return bouquets == m\n\n l, r = 1, max(bloomDay)\n while l < r:\n days = l + (r-l)//2\n if isEnoughDays(days):\n r = days\n else:\n l = days + 1\n \n return l\n\n\n \n``` | 5 | You are given an integer array `bloomDay`, an integer `m` and an integer `k`.
You want to make `m` bouquets. To make a bouquet, you need to use `k` **adjacent flowers** from the garden.
The garden consists of `n` flowers, the `ith` flower will bloom in the `bloomDay[i]` and then can be used in **exactly one** bouquet.
Return _the minimum number of days you need to wait to be able to make_ `m` _bouquets from the garden_. If it is impossible to make m bouquets return `-1`.
**Example 1:**
**Input:** bloomDay = \[1,10,3,10,2\], m = 3, k = 1
**Output:** 3
**Explanation:** Let us see what happened in the first three days. x means flower bloomed and \_ means flower did not bloom in the garden.
We need 3 bouquets each should contain 1 flower.
After day 1: \[x, \_, \_, \_, \_\] // we can only make one bouquet.
After day 2: \[x, \_, \_, \_, x\] // we can only make two bouquets.
After day 3: \[x, \_, x, \_, x\] // we can make 3 bouquets. The answer is 3.
**Example 2:**
**Input:** bloomDay = \[1,10,3,10,2\], m = 3, k = 2
**Output:** -1
**Explanation:** We need 3 bouquets each has 2 flowers, that means we need 6 flowers. We only have 5 flowers so it is impossible to get the needed bouquets and we return -1.
**Example 3:**
**Input:** bloomDay = \[7,7,7,7,12,7,7\], m = 2, k = 3
**Output:** 12
**Explanation:** We need 2 bouquets each should have 3 flowers.
Here is the garden after the 7 and 12 days:
After day 7: \[x, x, x, x, \_, x, x\]
We can make one bouquet of the first three flowers that bloomed. We cannot make another bouquet from the last three flowers that bloomed because they are not adjacent.
After day 12: \[x, x, x, x, x, x, x\]
It is obvious that we can make two bouquets in different ways.
**Constraints:**
* `bloomDay.length == n`
* `1 <= n <= 105`
* `1 <= bloomDay[i] <= 109`
* `1 <= m <= 106`
* `1 <= k <= n` | Brute force for each array element. In order to improve the time complexity, we can sort the array and get the answer for each array element. |
🔥[Python 3] Binary search, beats 95% 🥷🏼 | minimum-number-of-days-to-make-m-bouquets | 0 | 1 | ```python3 []\nclass Solution:\n def minDays(self, bloomDay: List[int], m: int, k: int) -> int:\n if len(bloomDay) < m * k: return -1\n\n def isEnoughDays(days):\n flowers, bouquets = 0, 0\n for d in bloomDay:\n flowers = flowers + 1 if d <= days else 0\n if flowers == k:\n bouquets += 1\n if bouquets == m: break\n flowers = 0\n \n return bouquets == m\n\n l, r = 1, max(bloomDay)\n while l < r:\n days = l + (r-l)//2\n if isEnoughDays(days):\n r = days\n else:\n l = days + 1\n \n return l\n\n\n \n``` | 5 | You are given two arrays `rowSum` and `colSum` of non-negative integers where `rowSum[i]` is the sum of the elements in the `ith` row and `colSum[j]` is the sum of the elements of the `jth` column of a 2D matrix. In other words, you do not know the elements of the matrix, but you do know the sums of each row and column.
Find any matrix of **non-negative** integers of size `rowSum.length x colSum.length` that satisfies the `rowSum` and `colSum` requirements.
Return _a 2D array representing **any** matrix that fulfills the requirements_. It's guaranteed that **at least one** matrix that fulfills the requirements exists.
**Example 1:**
**Input:** rowSum = \[3,8\], colSum = \[4,7\]
**Output:** \[\[3,0\],
\[1,7\]\]
**Explanation:**
0th row: 3 + 0 = 3 == rowSum\[0\]
1st row: 1 + 7 = 8 == rowSum\[1\]
0th column: 3 + 1 = 4 == colSum\[0\]
1st column: 0 + 7 = 7 == colSum\[1\]
The row and column sums match, and all matrix elements are non-negative.
Another possible matrix is: \[\[1,2\],
\[3,5\]\]
**Example 2:**
**Input:** rowSum = \[5,7,10\], colSum = \[8,6,8\]
**Output:** \[\[0,5,0\],
\[6,1,0\],
\[2,0,8\]\]
**Constraints:**
* `1 <= rowSum.length, colSum.length <= 500`
* `0 <= rowSum[i], colSum[i] <= 108`
* `sum(rowSum) == sum(colSum)` | If we can make m or more bouquets at day x, then we can still make m or more bouquets at any day y > x. We can check easily if we can make enough bouquets at day x if we can get group adjacent flowers at day x. |
Binary Search | Time: O(n*log(n)) | Space: O(1) | minimum-number-of-days-to-make-m-bouquets | 0 | 1 | # Intuition\nSince bloomDay[i] represents the day after flower will bloom. For example if bloomDay[i] = 2, the flower will be available after 2 days. Now we have to make bouquet of size "k", we need k adjacent flowers. From this we can conclude that we can form bouquet only in the range min(bloomDay) to max(bloomDay). Since we have low and high endpoints to form a bouquet, we can search through min and max bloomDay using binary Search. \n\n# Algorithm:\nWhile minDay <= maxDay repeat:\n\nStep 1: Calculate midDay = (minDay + maxday) / 2 <br>\nStep 2: For day in bloomDay:\n - If day <= midDay i.e. flower is available to form bouquet. If this is the first available flower then increment flower_count by 1 and adjacent to True. Else if already adjacent is True i.e. previous flower is also available then just increment count by 1\n - Else if day > midDay i.e. flower is not ready yet we will reset the count to 0 and adjacent to False\n - After above calculation we will check if count is equal to "k" then it means we can form a bouquet, so increment bouquet_count and reset count and adjacent variables <br>\nStep 3: If bouquet_count >= m: i.e. we found a solution so we will store the min of previos solution and current one. and look for better solution in less days. So we will search through left half of current search space.\nElse We didn\'t found solution yet so we will search through right half of search space.\n\n# Complexity\n- Time complexity:\n- For Binary Search log(n) and in each iteration of binary search we iterate through given array so overall complexity becomes: \nO(n * log(n))\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def minDays(self, bloomDay: List[int], m: int, k: int) -> int:\n if m*k > len(bloomDay):\n return -1\n\n min_value, max_value = min(bloomDay), max(bloomDay)\n answer = max_value\n\n while min_value <= max_value:\n mid = (min_value + max_value) // 2\n\n count, bouquets, adjacent = 0, 0, False\n for i in range(len(bloomDay)):\n if bloomDay[i] <= mid:\n if count == 0:\n adjacent = True\n count += 1\n elif adjacent:\n count += 1\n else:\n count = 0\n adjacent = False\n \n if count == k:\n bouquets += 1\n count, adjacent = 0, False\n \n if bouquets >= m:\n answer = min(answer, mid)\n max_value = mid - 1\n else:\n min_value = mid + 1\n \n return answer\n``` | 2 | You are given an integer array `bloomDay`, an integer `m` and an integer `k`.
You want to make `m` bouquets. To make a bouquet, you need to use `k` **adjacent flowers** from the garden.
The garden consists of `n` flowers, the `ith` flower will bloom in the `bloomDay[i]` and then can be used in **exactly one** bouquet.
Return _the minimum number of days you need to wait to be able to make_ `m` _bouquets from the garden_. If it is impossible to make m bouquets return `-1`.
**Example 1:**
**Input:** bloomDay = \[1,10,3,10,2\], m = 3, k = 1
**Output:** 3
**Explanation:** Let us see what happened in the first three days. x means flower bloomed and \_ means flower did not bloom in the garden.
We need 3 bouquets each should contain 1 flower.
After day 1: \[x, \_, \_, \_, \_\] // we can only make one bouquet.
After day 2: \[x, \_, \_, \_, x\] // we can only make two bouquets.
After day 3: \[x, \_, x, \_, x\] // we can make 3 bouquets. The answer is 3.
**Example 2:**
**Input:** bloomDay = \[1,10,3,10,2\], m = 3, k = 2
**Output:** -1
**Explanation:** We need 3 bouquets each has 2 flowers, that means we need 6 flowers. We only have 5 flowers so it is impossible to get the needed bouquets and we return -1.
**Example 3:**
**Input:** bloomDay = \[7,7,7,7,12,7,7\], m = 2, k = 3
**Output:** 12
**Explanation:** We need 2 bouquets each should have 3 flowers.
Here is the garden after the 7 and 12 days:
After day 7: \[x, x, x, x, \_, x, x\]
We can make one bouquet of the first three flowers that bloomed. We cannot make another bouquet from the last three flowers that bloomed because they are not adjacent.
After day 12: \[x, x, x, x, x, x, x\]
It is obvious that we can make two bouquets in different ways.
**Constraints:**
* `bloomDay.length == n`
* `1 <= n <= 105`
* `1 <= bloomDay[i] <= 109`
* `1 <= m <= 106`
* `1 <= k <= n` | Brute force for each array element. In order to improve the time complexity, we can sort the array and get the answer for each array element. |
Binary Search | Time: O(n*log(n)) | Space: O(1) | minimum-number-of-days-to-make-m-bouquets | 0 | 1 | # Intuition\nSince bloomDay[i] represents the day after flower will bloom. For example if bloomDay[i] = 2, the flower will be available after 2 days. Now we have to make bouquet of size "k", we need k adjacent flowers. From this we can conclude that we can form bouquet only in the range min(bloomDay) to max(bloomDay). Since we have low and high endpoints to form a bouquet, we can search through min and max bloomDay using binary Search. \n\n# Algorithm:\nWhile minDay <= maxDay repeat:\n\nStep 1: Calculate midDay = (minDay + maxday) / 2 <br>\nStep 2: For day in bloomDay:\n - If day <= midDay i.e. flower is available to form bouquet. If this is the first available flower then increment flower_count by 1 and adjacent to True. Else if already adjacent is True i.e. previous flower is also available then just increment count by 1\n - Else if day > midDay i.e. flower is not ready yet we will reset the count to 0 and adjacent to False\n - After above calculation we will check if count is equal to "k" then it means we can form a bouquet, so increment bouquet_count and reset count and adjacent variables <br>\nStep 3: If bouquet_count >= m: i.e. we found a solution so we will store the min of previos solution and current one. and look for better solution in less days. So we will search through left half of current search space.\nElse We didn\'t found solution yet so we will search through right half of search space.\n\n# Complexity\n- Time complexity:\n- For Binary Search log(n) and in each iteration of binary search we iterate through given array so overall complexity becomes: \nO(n * log(n))\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def minDays(self, bloomDay: List[int], m: int, k: int) -> int:\n if m*k > len(bloomDay):\n return -1\n\n min_value, max_value = min(bloomDay), max(bloomDay)\n answer = max_value\n\n while min_value <= max_value:\n mid = (min_value + max_value) // 2\n\n count, bouquets, adjacent = 0, 0, False\n for i in range(len(bloomDay)):\n if bloomDay[i] <= mid:\n if count == 0:\n adjacent = True\n count += 1\n elif adjacent:\n count += 1\n else:\n count = 0\n adjacent = False\n \n if count == k:\n bouquets += 1\n count, adjacent = 0, False\n \n if bouquets >= m:\n answer = min(answer, mid)\n max_value = mid - 1\n else:\n min_value = mid + 1\n \n return answer\n``` | 2 | You are given two arrays `rowSum` and `colSum` of non-negative integers where `rowSum[i]` is the sum of the elements in the `ith` row and `colSum[j]` is the sum of the elements of the `jth` column of a 2D matrix. In other words, you do not know the elements of the matrix, but you do know the sums of each row and column.
Find any matrix of **non-negative** integers of size `rowSum.length x colSum.length` that satisfies the `rowSum` and `colSum` requirements.
Return _a 2D array representing **any** matrix that fulfills the requirements_. It's guaranteed that **at least one** matrix that fulfills the requirements exists.
**Example 1:**
**Input:** rowSum = \[3,8\], colSum = \[4,7\]
**Output:** \[\[3,0\],
\[1,7\]\]
**Explanation:**
0th row: 3 + 0 = 3 == rowSum\[0\]
1st row: 1 + 7 = 8 == rowSum\[1\]
0th column: 3 + 1 = 4 == colSum\[0\]
1st column: 0 + 7 = 7 == colSum\[1\]
The row and column sums match, and all matrix elements are non-negative.
Another possible matrix is: \[\[1,2\],
\[3,5\]\]
**Example 2:**
**Input:** rowSum = \[5,7,10\], colSum = \[8,6,8\]
**Output:** \[\[0,5,0\],
\[6,1,0\],
\[2,0,8\]\]
**Constraints:**
* `1 <= rowSum.length, colSum.length <= 500`
* `0 <= rowSum[i], colSum[i] <= 108`
* `sum(rowSum) == sum(colSum)` | If we can make m or more bouquets at day x, then we can still make m or more bouquets at any day y > x. We can check easily if we can make enough bouquets at day x if we can get group adjacent flowers at day x. |
Most optimal solution with explanation using binary search | minimum-number-of-days-to-make-m-bouquets | 1 | 1 | \n\n# Approach\nThe solution uses binary search to find the minimum number of days needed to make m bouquets using k adjacent flowers from the garden. The key idea is to perform a binary search on the possible days within which the flowers can bloom, and then check whether it\'s possible to make at least m bouquets using those bloomed flowers.\n\n- The possible function takes the list of bloom days, a specific day day, the required number of bouquets m, and the number of flowers needed for a bouquet k.\n\n- It iterates through the bloomDay list and counts how many flowers have bloomed within the day limit. When a flower\'s bloom day is greater than day, it resets the cnt (count) and adds the count of complete bouquets that can be formed from the flowers that bloomed before this day.\n\n- After the loop, it calculates the total number of bouquets that can be formed using the remaining flowers.\n\n- The minDays function takes the bloomDay list, the required number of bouquets m, and the number of flowers needed for a bouquet k.\n\n- It calculates the val as the minimum number of flowers required to make m bouquets.\n\n- It finds the lowest and highest bloom days in the bloomDay list.\n\n- The binary search is performed within the range of bloom days from low to high. Inside the loop, it checks if it\'s possible to make m bouquets with k flowers each, using flowers that bloom within the mid day. If possible, it updates high to mid-1, else it updates low to mid+1.\n\n- Finally, it returns the low value, which represents the minimum number of days needed to make m bouquets using k adjacent flowers.\n\n# Complexity\n- Time complexity:\nO(n*log(max-min))\n\n- Space complexity:\nO(1)\n\n```C++ []\nclass Solution {\npublic:\n bool possible(vector<int>& nums, int day, int m, int k) {\n int cnt = 0, num = 0;\n for(int i = 0; i< nums.size(); i++) {\n if(nums[i] <= day) cnt++;\n else {\n num += cnt/k;\n cnt = 0;\n }\n }\n num += cnt/k;\n return num>=m;\n }\n int minDays(vector<int>& bloomDay, int m, int k) {\n int n = bloomDay.size();\n long long val = m * 1ll * k * 1ll;\n if(val>n) return -1;\n int low = INT_MAX, high = INT_MIN;\n for(int i = 0; i< n; i++) {\n low = min(bloomDay[i], low);\n high = max(bloomDay[i], high);\n }\n while(low<=high) {\n int mid = (low+high)/2;\n if(possible(bloomDay, mid, m, k)) high = mid-1;\n else low = mid+1;\n }\n return low;\n }\n};\n```\n```python []\nclass Solution:\n def minDays(self, bloomDay: List[int], m: int, k: int) -> int:\n n = len(bloomDay)\n val = m * k\n if val > n:\n return -1\n \n low = float(\'inf\')\n high = float(\'-inf\')\n for day in bloomDay:\n low = min(day, low)\n high = max(day, high)\n \n while low <= high:\n mid = low + (high - low) // 2\n if self.possible(bloomDay, mid, m, k):\n high = mid - 1\n else:\n low = mid + 1\n \n return low\n \n def possible(self, bloomDay, day, m, k):\n cnt = 0\n num = 0\n for bd in bloomDay:\n if bd <= day:\n cnt += 1\n else:\n num += cnt // k\n cnt = 0\n num += cnt // k\n return num >= m\n\n```\n```JAVA []\nclass Solution {\n public int minDays(int[] bloomDay, int m, int k) {\n int n = bloomDay.length;\n long val = (long) m * k;\n if (val > n) return -1;\n \n int low = Integer.MAX_VALUE, high = Integer.MIN_VALUE;\n for (int day : bloomDay) {\n low = Math.min(day, low);\n high = Math.max(day, high);\n }\n \n while (low <= high) {\n int mid = low + (high - low) / 2;\n if (possible(bloomDay, mid, m, k)) {\n high = mid - 1;\n } else {\n low = mid + 1;\n }\n }\n \n return low;\n }\n \n private boolean possible(int[] bloomDay, int day, int m, int k) {\n int cnt = 0, num = 0;\n for (int i = 0; i < bloomDay.length; i++) {\n if (bloomDay[i] <= day) {\n cnt++;\n } else {\n num += cnt / k;\n cnt = 0;\n }\n }\n num += cnt / k;\n return num >= m;\n }\n}\n\n```\n | 5 | You are given an integer array `bloomDay`, an integer `m` and an integer `k`.
You want to make `m` bouquets. To make a bouquet, you need to use `k` **adjacent flowers** from the garden.
The garden consists of `n` flowers, the `ith` flower will bloom in the `bloomDay[i]` and then can be used in **exactly one** bouquet.
Return _the minimum number of days you need to wait to be able to make_ `m` _bouquets from the garden_. If it is impossible to make m bouquets return `-1`.
**Example 1:**
**Input:** bloomDay = \[1,10,3,10,2\], m = 3, k = 1
**Output:** 3
**Explanation:** Let us see what happened in the first three days. x means flower bloomed and \_ means flower did not bloom in the garden.
We need 3 bouquets each should contain 1 flower.
After day 1: \[x, \_, \_, \_, \_\] // we can only make one bouquet.
After day 2: \[x, \_, \_, \_, x\] // we can only make two bouquets.
After day 3: \[x, \_, x, \_, x\] // we can make 3 bouquets. The answer is 3.
**Example 2:**
**Input:** bloomDay = \[1,10,3,10,2\], m = 3, k = 2
**Output:** -1
**Explanation:** We need 3 bouquets each has 2 flowers, that means we need 6 flowers. We only have 5 flowers so it is impossible to get the needed bouquets and we return -1.
**Example 3:**
**Input:** bloomDay = \[7,7,7,7,12,7,7\], m = 2, k = 3
**Output:** 12
**Explanation:** We need 2 bouquets each should have 3 flowers.
Here is the garden after the 7 and 12 days:
After day 7: \[x, x, x, x, \_, x, x\]
We can make one bouquet of the first three flowers that bloomed. We cannot make another bouquet from the last three flowers that bloomed because they are not adjacent.
After day 12: \[x, x, x, x, x, x, x\]
It is obvious that we can make two bouquets in different ways.
**Constraints:**
* `bloomDay.length == n`
* `1 <= n <= 105`
* `1 <= bloomDay[i] <= 109`
* `1 <= m <= 106`
* `1 <= k <= n` | Brute force for each array element. In order to improve the time complexity, we can sort the array and get the answer for each array element. |
Most optimal solution with explanation using binary search | minimum-number-of-days-to-make-m-bouquets | 1 | 1 | \n\n# Approach\nThe solution uses binary search to find the minimum number of days needed to make m bouquets using k adjacent flowers from the garden. The key idea is to perform a binary search on the possible days within which the flowers can bloom, and then check whether it\'s possible to make at least m bouquets using those bloomed flowers.\n\n- The possible function takes the list of bloom days, a specific day day, the required number of bouquets m, and the number of flowers needed for a bouquet k.\n\n- It iterates through the bloomDay list and counts how many flowers have bloomed within the day limit. When a flower\'s bloom day is greater than day, it resets the cnt (count) and adds the count of complete bouquets that can be formed from the flowers that bloomed before this day.\n\n- After the loop, it calculates the total number of bouquets that can be formed using the remaining flowers.\n\n- The minDays function takes the bloomDay list, the required number of bouquets m, and the number of flowers needed for a bouquet k.\n\n- It calculates the val as the minimum number of flowers required to make m bouquets.\n\n- It finds the lowest and highest bloom days in the bloomDay list.\n\n- The binary search is performed within the range of bloom days from low to high. Inside the loop, it checks if it\'s possible to make m bouquets with k flowers each, using flowers that bloom within the mid day. If possible, it updates high to mid-1, else it updates low to mid+1.\n\n- Finally, it returns the low value, which represents the minimum number of days needed to make m bouquets using k adjacent flowers.\n\n# Complexity\n- Time complexity:\nO(n*log(max-min))\n\n- Space complexity:\nO(1)\n\n```C++ []\nclass Solution {\npublic:\n bool possible(vector<int>& nums, int day, int m, int k) {\n int cnt = 0, num = 0;\n for(int i = 0; i< nums.size(); i++) {\n if(nums[i] <= day) cnt++;\n else {\n num += cnt/k;\n cnt = 0;\n }\n }\n num += cnt/k;\n return num>=m;\n }\n int minDays(vector<int>& bloomDay, int m, int k) {\n int n = bloomDay.size();\n long long val = m * 1ll * k * 1ll;\n if(val>n) return -1;\n int low = INT_MAX, high = INT_MIN;\n for(int i = 0; i< n; i++) {\n low = min(bloomDay[i], low);\n high = max(bloomDay[i], high);\n }\n while(low<=high) {\n int mid = (low+high)/2;\n if(possible(bloomDay, mid, m, k)) high = mid-1;\n else low = mid+1;\n }\n return low;\n }\n};\n```\n```python []\nclass Solution:\n def minDays(self, bloomDay: List[int], m: int, k: int) -> int:\n n = len(bloomDay)\n val = m * k\n if val > n:\n return -1\n \n low = float(\'inf\')\n high = float(\'-inf\')\n for day in bloomDay:\n low = min(day, low)\n high = max(day, high)\n \n while low <= high:\n mid = low + (high - low) // 2\n if self.possible(bloomDay, mid, m, k):\n high = mid - 1\n else:\n low = mid + 1\n \n return low\n \n def possible(self, bloomDay, day, m, k):\n cnt = 0\n num = 0\n for bd in bloomDay:\n if bd <= day:\n cnt += 1\n else:\n num += cnt // k\n cnt = 0\n num += cnt // k\n return num >= m\n\n```\n```JAVA []\nclass Solution {\n public int minDays(int[] bloomDay, int m, int k) {\n int n = bloomDay.length;\n long val = (long) m * k;\n if (val > n) return -1;\n \n int low = Integer.MAX_VALUE, high = Integer.MIN_VALUE;\n for (int day : bloomDay) {\n low = Math.min(day, low);\n high = Math.max(day, high);\n }\n \n while (low <= high) {\n int mid = low + (high - low) / 2;\n if (possible(bloomDay, mid, m, k)) {\n high = mid - 1;\n } else {\n low = mid + 1;\n }\n }\n \n return low;\n }\n \n private boolean possible(int[] bloomDay, int day, int m, int k) {\n int cnt = 0, num = 0;\n for (int i = 0; i < bloomDay.length; i++) {\n if (bloomDay[i] <= day) {\n cnt++;\n } else {\n num += cnt / k;\n cnt = 0;\n }\n }\n num += cnt / k;\n return num >= m;\n }\n}\n\n```\n | 5 | You are given two arrays `rowSum` and `colSum` of non-negative integers where `rowSum[i]` is the sum of the elements in the `ith` row and `colSum[j]` is the sum of the elements of the `jth` column of a 2D matrix. In other words, you do not know the elements of the matrix, but you do know the sums of each row and column.
Find any matrix of **non-negative** integers of size `rowSum.length x colSum.length` that satisfies the `rowSum` and `colSum` requirements.
Return _a 2D array representing **any** matrix that fulfills the requirements_. It's guaranteed that **at least one** matrix that fulfills the requirements exists.
**Example 1:**
**Input:** rowSum = \[3,8\], colSum = \[4,7\]
**Output:** \[\[3,0\],
\[1,7\]\]
**Explanation:**
0th row: 3 + 0 = 3 == rowSum\[0\]
1st row: 1 + 7 = 8 == rowSum\[1\]
0th column: 3 + 1 = 4 == colSum\[0\]
1st column: 0 + 7 = 7 == colSum\[1\]
The row and column sums match, and all matrix elements are non-negative.
Another possible matrix is: \[\[1,2\],
\[3,5\]\]
**Example 2:**
**Input:** rowSum = \[5,7,10\], colSum = \[8,6,8\]
**Output:** \[\[0,5,0\],
\[6,1,0\],
\[2,0,8\]\]
**Constraints:**
* `1 <= rowSum.length, colSum.length <= 500`
* `0 <= rowSum[i], colSum[i] <= 108`
* `sum(rowSum) == sum(colSum)` | If we can make m or more bouquets at day x, then we can still make m or more bouquets at any day y > x. We can check easily if we can make enough bouquets at day x if we can get group adjacent flowers at day x. |
Elegant solution, detailed explanation with illustrations!! C++, python3, python | kth-ancestor-of-a-tree-node | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe first thing that comes to mind is to just go up $k$ times for each $getKthAncestor$ query. But the time complexity of that approach would be $O(q*k)$ where $q$ is the number of queries. So going up 1 step at a time is too slow. So think of how can we go up with bigger steps.\n\n<b>Hint 1:</b> Consider the option of precomputing a set of ancestors for each node and then utilizing that set to ascend by more than one step at a time while responding to the queries.\n\n<b>Hint 2:</b> Those sets should consist of ancestors that are a power of two edges away, namely the $2^i$th ancestors ($i\\geq0$) of each node.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst, we need to calculate $2^i$th ($0\\leq i\\leq log_{2}n$) ancesstors for each node $v$.\nTo do that we can use dynamic programing approach.\nLet $anc[i][v]$ denote the $2^i$th ancestor of $v$\nif $i=0$: \n$\\quad$ $2^0=1$, $1$st ancestor of $v$ is just $parent[v]$, thus, $anc[0][v]=parent[v]$\nif $i\\gt0$: \n$\\quad$ Assume that we calculated the $2^{i-1}$th ancestor of each node and now we want to calculate the $2^i$th ancestor of node $v$. Notice that going up $2^i$ times is the same as going up $2^{i-1}$ times twice as $2*2^{i-1}=2^i$\n$\\quad$ Let $u$ be the $2^{i-1}$th ancestor of $v$. We have already stored the value of $u$ in $anc[i-1][v]$ and can access that value in $O(1)$. If $u=-1$, meaning that $v$ doesn\'t have a $2^{i-1}$th ancestor, then $v$ doesn\'t have a $2^i$th ancestor either, and we set $anc[i][v]=-1$. However, if $u$ isn\'t $-1$, then we can find the $2^{i-1}$th ancestor of $u$, which we have already calculated and stored in $anc[i-1][u]$. Therefore, we can set $anc[i][v]=anc[i-1][u]=anc[i-1][anc[i-1][v]]$, and this computation also takes $O(1)$ time.\nNotice that we calculate $log_{2}n$*$n$ values each in $O(1)$. Therefore, the complexity of calculating the array $anc$ is $O(nlog_2n)$\n\n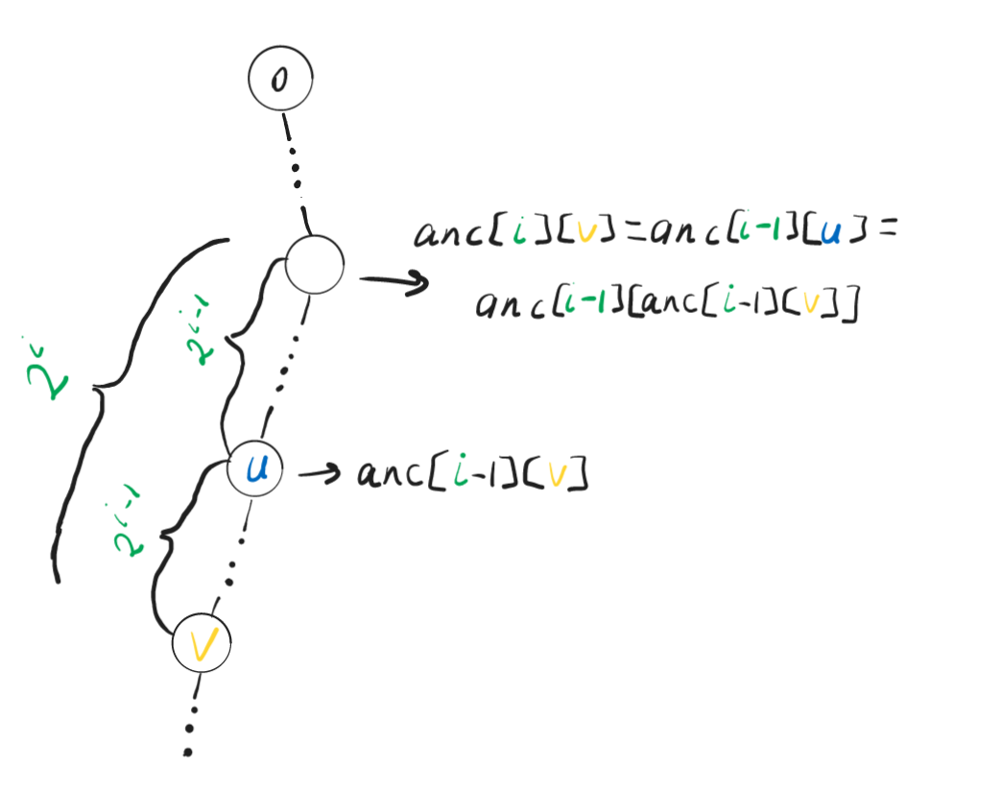\n\nAfter creating the $anc$ array, now we need to answer the queries. For instance, consider the query where $k=28$. Instead of going up $28$ times using the $parent$ array, we can utilize the $anc$ array. Notice that $28$ can be represented as the sum of powers of $2$: $28=2^2+2^3+2^4$. Thus, we can find the $28$th ancestor of a given node in just $3$ steps instead of $28$! First, we find the $2^2$nd ancestor of the initial node. Then we find the $2^3$rd ancestor of that ancestor. Finally, we find the $2^4$th ancestor of that second ancestor.\n\n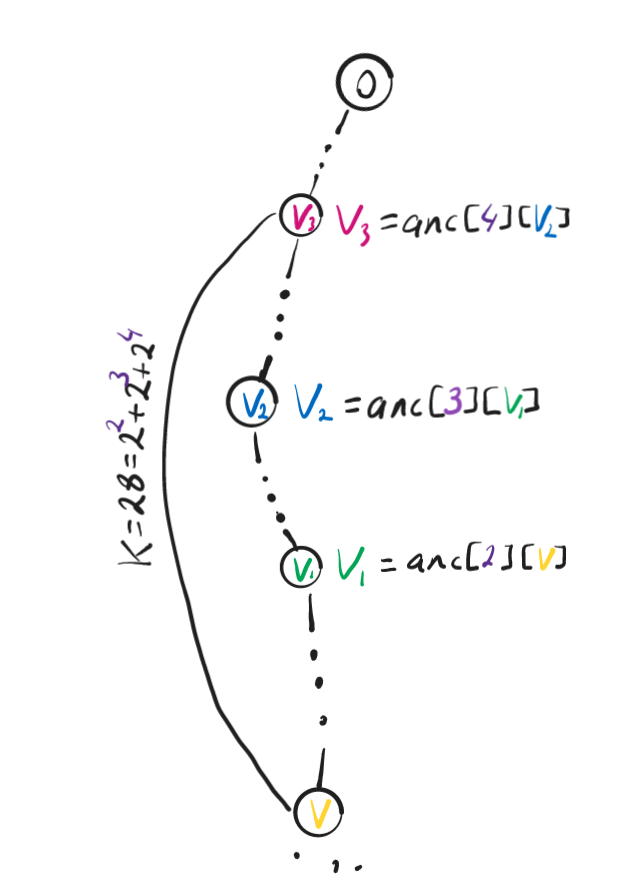\n\nThe general case:\nWe need to iterate through the bits of $k$ and update $v$ accordingly. That is if $i$th bit of $k$ is $1$ we need to update $v:=anc[i][v]$. And if $v$ becomes $-1$ at some point we can return $-1$ instantly. The implementation of it would look like this:\n```cpp []\n for (int i = 0; i <= log(k); i++) {\n if (node == -1)\n return -1;\n if ((1 << i) & k)\n node = anc[i][node];\n }\n```\n```python3 []\n for i in range(log(k)):\n if node == -1:\n return -1\n if (1 << i) & k:\n node = anc[i][node]\n```\n```python []\n for i in range(log(k)):\n if node == -1:\n return -1\n if (1 << i) & k:\n node = anc[i][node]\n```\nWe answer each query in $O(log_2{k})$.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$\\quad$ The complexity of calculating the $anc$ array - $O(nlog_2{n})$\n$\\quad$ The worst case complexity of answering each query is $O(log_2n)$ as $k\\leq n$. So the overall complextity of answering questions will be $O(qlog_2n)$, where $q$ is the number of queries.\n$\\quad$ Therefore, the time complexity of this solution is $O(nlog_2n+qlog_2n)$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$\\quad$ The only space used is the array $anc$, which has $O(nlog_2n)$ space somplexity. That is storing $log_2n$ ancestors for each node and the number of nodes is $n$.\n\nPlease upvote if you found it helpful, thank you!!\n# Code\n```cpp []\nclass TreeAncestor {\n public:\n vector<int> anc[16]; //16 == max(log(n))\n TreeAncestor(int n, vector<int> &parent) {\n anc[0] = parent;\n for (int i = 1; i < 16; i++) {\n anc[i].resize(n);\n for (int v = 0; v < n; v++) {\n if (anc[i - 1][v] == -1)\n anc[i][v] = -1;\n else\n anc[i][v] = anc[i - 1][anc[i - 1][v]];\n }\n }\n }\n\n int getKthAncestor(int node, int k) {\n for (int i = 0; i < 16; i++) {\n if (node == -1)\n return -1;\n if ((1 << i) & k)\n node = anc[i][node];\n }\n return node;\n }\n};\n\n/**\n * Your TreeAncestor object will be instantiated and called as such:\n * TreeAncestor* obj = new TreeAncestor(n, parent);\n * int param_1 = obj->getKthAncestor(node,k);\n */\n```\n```python3 []\nclass TreeAncestor:\n\n def __init__(self, n: int, parent: List[int]):\n self.anc = [[parent[i] for i in range(n)]]\n for i in range(1, 16): # 16 == max(log(n))\n self.anc.append([])\n for v in range(n):\n if self.anc[i-1][v]==-1:\n self.anc[i].append(-1)\n else:\n self.anc[i].append(self.anc[i-1][self.anc[i-1][v]])\n\n def getKthAncestor(self, node: int, k: int) -> int:\n for i in range(16):\n if node == -1:\n return -1\n if (1<<i)&k:\n node=self.anc[i][node]\n return node\n\n\n# Your TreeAncestor object will be instantiated and called as such:\n# obj = TreeAncestor(n, parent)\n# param_1 = obj.getKthAncestor(node,k)\n```\n``` python []\nclass TreeAncestor(object):\n\n def __init__(self, n, parent):\n """\n :type n: int\n :type parent: List[int]\n """\n self.anc = [[parent[i] for i in range(n)]]\n for i in range(1, 16):\n self.anc.append([])\n for v in range(n):\n if self.anc[i-1][v]==-1:\n self.anc[i].append(-1)\n else:\n self.anc[i].append(self.anc[i-1][self.anc[i-1][v]])\n \n\n def getKthAncestor(self, node, k):\n """\n :type node: int\n :type k: int\n :rtype: int\n """\n for i in range(16):\n if node == -1:\n return -1\n if (1<<i)&k:\n node=self.anc[i][node]\n return node\n\n\n# Your TreeAncestor object will be instantiated and called as such:\n# obj = TreeAncestor(n, parent)\n# param_1 = obj.getKthAncestor(node,k)\n```\n\n | 9 | You are given a tree with `n` nodes numbered from `0` to `n - 1` in the form of a parent array `parent` where `parent[i]` is the parent of `ith` node. The root of the tree is node `0`. Find the `kth` ancestor of a given node.
The `kth` ancestor of a tree node is the `kth` node in the path from that node to the root node.
Implement the `TreeAncestor` class:
* `TreeAncestor(int n, int[] parent)` Initializes the object with the number of nodes in the tree and the parent array.
* `int getKthAncestor(int node, int k)` return the `kth` ancestor of the given node `node`. If there is no such ancestor, return `-1`.
**Example 1:**
**Input**
\[ "TreeAncestor ", "getKthAncestor ", "getKthAncestor ", "getKthAncestor "\]
\[\[7, \[-1, 0, 0, 1, 1, 2, 2\]\], \[3, 1\], \[5, 2\], \[6, 3\]\]
**Output**
\[null, 1, 0, -1\]
**Explanation**
TreeAncestor treeAncestor = new TreeAncestor(7, \[-1, 0, 0, 1, 1, 2, 2\]);
treeAncestor.getKthAncestor(3, 1); // returns 1 which is the parent of 3
treeAncestor.getKthAncestor(5, 2); // returns 0 which is the grandparent of 5
treeAncestor.getKthAncestor(6, 3); // returns -1 because there is no such ancestor
**Constraints:**
* `1 <= k <= n <= 5 * 104`
* `parent.length == n`
* `parent[0] == -1`
* `0 <= parent[i] < n` for all `0 < i < n`
* `0 <= node < n`
* There will be at most `5 * 104` queries. | Build array rank where rank[i][j] is the number of votes for team i to be the j-th rank. Sort the trams by rank array. if rank array is the same for two or more teams, sort them by the ID in ascending order. |
Elegant solution, detailed explanation with illustrations!! C++, python3, python | kth-ancestor-of-a-tree-node | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe first thing that comes to mind is to just go up $k$ times for each $getKthAncestor$ query. But the time complexity of that approach would be $O(q*k)$ where $q$ is the number of queries. So going up 1 step at a time is too slow. So think of how can we go up with bigger steps.\n\n<b>Hint 1:</b> Consider the option of precomputing a set of ancestors for each node and then utilizing that set to ascend by more than one step at a time while responding to the queries.\n\n<b>Hint 2:</b> Those sets should consist of ancestors that are a power of two edges away, namely the $2^i$th ancestors ($i\\geq0$) of each node.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst, we need to calculate $2^i$th ($0\\leq i\\leq log_{2}n$) ancesstors for each node $v$.\nTo do that we can use dynamic programing approach.\nLet $anc[i][v]$ denote the $2^i$th ancestor of $v$\nif $i=0$: \n$\\quad$ $2^0=1$, $1$st ancestor of $v$ is just $parent[v]$, thus, $anc[0][v]=parent[v]$\nif $i\\gt0$: \n$\\quad$ Assume that we calculated the $2^{i-1}$th ancestor of each node and now we want to calculate the $2^i$th ancestor of node $v$. Notice that going up $2^i$ times is the same as going up $2^{i-1}$ times twice as $2*2^{i-1}=2^i$\n$\\quad$ Let $u$ be the $2^{i-1}$th ancestor of $v$. We have already stored the value of $u$ in $anc[i-1][v]$ and can access that value in $O(1)$. If $u=-1$, meaning that $v$ doesn\'t have a $2^{i-1}$th ancestor, then $v$ doesn\'t have a $2^i$th ancestor either, and we set $anc[i][v]=-1$. However, if $u$ isn\'t $-1$, then we can find the $2^{i-1}$th ancestor of $u$, which we have already calculated and stored in $anc[i-1][u]$. Therefore, we can set $anc[i][v]=anc[i-1][u]=anc[i-1][anc[i-1][v]]$, and this computation also takes $O(1)$ time.\nNotice that we calculate $log_{2}n$*$n$ values each in $O(1)$. Therefore, the complexity of calculating the array $anc$ is $O(nlog_2n)$\n\n\n\nAfter creating the $anc$ array, now we need to answer the queries. For instance, consider the query where $k=28$. Instead of going up $28$ times using the $parent$ array, we can utilize the $anc$ array. Notice that $28$ can be represented as the sum of powers of $2$: $28=2^2+2^3+2^4$. Thus, we can find the $28$th ancestor of a given node in just $3$ steps instead of $28$! First, we find the $2^2$nd ancestor of the initial node. Then we find the $2^3$rd ancestor of that ancestor. Finally, we find the $2^4$th ancestor of that second ancestor.\n\n\n\nThe general case:\nWe need to iterate through the bits of $k$ and update $v$ accordingly. That is if $i$th bit of $k$ is $1$ we need to update $v:=anc[i][v]$. And if $v$ becomes $-1$ at some point we can return $-1$ instantly. The implementation of it would look like this:\n```cpp []\n for (int i = 0; i <= log(k); i++) {\n if (node == -1)\n return -1;\n if ((1 << i) & k)\n node = anc[i][node];\n }\n```\n```python3 []\n for i in range(log(k)):\n if node == -1:\n return -1\n if (1 << i) & k:\n node = anc[i][node]\n```\n```python []\n for i in range(log(k)):\n if node == -1:\n return -1\n if (1 << i) & k:\n node = anc[i][node]\n```\nWe answer each query in $O(log_2{k})$.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$\\quad$ The complexity of calculating the $anc$ array - $O(nlog_2{n})$\n$\\quad$ The worst case complexity of answering each query is $O(log_2n)$ as $k\\leq n$. So the overall complextity of answering questions will be $O(qlog_2n)$, where $q$ is the number of queries.\n$\\quad$ Therefore, the time complexity of this solution is $O(nlog_2n+qlog_2n)$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$\\quad$ The only space used is the array $anc$, which has $O(nlog_2n)$ space somplexity. That is storing $log_2n$ ancestors for each node and the number of nodes is $n$.\n\nPlease upvote if you found it helpful, thank you!!\n# Code\n```cpp []\nclass TreeAncestor {\n public:\n vector<int> anc[16]; //16 == max(log(n))\n TreeAncestor(int n, vector<int> &parent) {\n anc[0] = parent;\n for (int i = 1; i < 16; i++) {\n anc[i].resize(n);\n for (int v = 0; v < n; v++) {\n if (anc[i - 1][v] == -1)\n anc[i][v] = -1;\n else\n anc[i][v] = anc[i - 1][anc[i - 1][v]];\n }\n }\n }\n\n int getKthAncestor(int node, int k) {\n for (int i = 0; i < 16; i++) {\n if (node == -1)\n return -1;\n if ((1 << i) & k)\n node = anc[i][node];\n }\n return node;\n }\n};\n\n/**\n * Your TreeAncestor object will be instantiated and called as such:\n * TreeAncestor* obj = new TreeAncestor(n, parent);\n * int param_1 = obj->getKthAncestor(node,k);\n */\n```\n```python3 []\nclass TreeAncestor:\n\n def __init__(self, n: int, parent: List[int]):\n self.anc = [[parent[i] for i in range(n)]]\n for i in range(1, 16): # 16 == max(log(n))\n self.anc.append([])\n for v in range(n):\n if self.anc[i-1][v]==-1:\n self.anc[i].append(-1)\n else:\n self.anc[i].append(self.anc[i-1][self.anc[i-1][v]])\n\n def getKthAncestor(self, node: int, k: int) -> int:\n for i in range(16):\n if node == -1:\n return -1\n if (1<<i)&k:\n node=self.anc[i][node]\n return node\n\n\n# Your TreeAncestor object will be instantiated and called as such:\n# obj = TreeAncestor(n, parent)\n# param_1 = obj.getKthAncestor(node,k)\n```\n``` python []\nclass TreeAncestor(object):\n\n def __init__(self, n, parent):\n """\n :type n: int\n :type parent: List[int]\n """\n self.anc = [[parent[i] for i in range(n)]]\n for i in range(1, 16):\n self.anc.append([])\n for v in range(n):\n if self.anc[i-1][v]==-1:\n self.anc[i].append(-1)\n else:\n self.anc[i].append(self.anc[i-1][self.anc[i-1][v]])\n \n\n def getKthAncestor(self, node, k):\n """\n :type node: int\n :type k: int\n :rtype: int\n """\n for i in range(16):\n if node == -1:\n return -1\n if (1<<i)&k:\n node=self.anc[i][node]\n return node\n\n\n# Your TreeAncestor object will be instantiated and called as such:\n# obj = TreeAncestor(n, parent)\n# param_1 = obj.getKthAncestor(node,k)\n```\n\n | 9 | Given an array of integers `nums` and a positive integer `k`, check whether it is possible to divide this array into sets of `k` consecutive numbers.
Return `true` _if it is possible_. Otherwise, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,3,4,4,5,6\], k = 4
**Output:** true
**Explanation:** Array can be divided into \[1,2,3,4\] and \[3,4,5,6\].
**Example 2:**
**Input:** nums = \[3,2,1,2,3,4,3,4,5,9,10,11\], k = 3
**Output:** true
**Explanation:** Array can be divided into \[1,2,3\] , \[2,3,4\] , \[3,4,5\] and \[9,10,11\].
**Example 3:**
**Input:** nums = \[1,2,3,4\], k = 3
**Output:** false
**Explanation:** Each array should be divided in subarrays of size 3.
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `1 <= nums[i] <= 109`
**Note:** This question is the same as 846: [https://leetcode.com/problems/hand-of-straights/](https://leetcode.com/problems/hand-of-straights/) | The queries must be answered efficiently to avoid time limit exceeded verdict. Use sparse table (dynamic programming application) to travel the tree upwards in a fast way. |
[Python3] binary lifting (dp) | kth-ancestor-of-a-tree-node | 0 | 1 | Algo\nFor node 0, 1, ..., n-1, we define a matrix `self.dp[][]` whose `i, j`th element indicates the `i`th node\'s `2^j` parent. Here, `i = 0, 1, ..., n-1` and `j = 0, 1, ..., int(log2(n))`. An important recursive relationship is that \n\n`self.dp[i][j] = self.dp[self.dp[i][j-1]][j-1]`. \n\nIn other words, `i`th node\'s `2^j` parent is `i`th node\'s `2^(j-1)` parent\'s `2^(j-1)` parent. In this way, lookup is guarenteed to complete in `O(logN)` time. Note that it takes `O(NlogN)` to build `self.dp`. \n\nTime complexity `O(NlogN)` to pre-processing the tree and `O(logN)` for each equery thereafter. \n```\nclass TreeAncestor:\n\n def __init__(self, n: int, parent: List[int]):\n m = 1 + int(log2(n)) #at most 16 for this problem \n self.dp = [[-1] * m for _ in range(n)] #ith node\'s 2^j parent\n for j in range(m):\n for i in range(n):\n if j == 0: self.dp[i][0] = parent[i] #2^0 parent\n elif self.dp[i][j-1] != -1: \n self.dp[i][j] = self.dp[self.dp[i][j-1]][j-1]\n \n def getKthAncestor(self, node: int, k: int) -> int:\n while k > 0 and node != -1: \n i = int(log2(k))\n node = self.dp[node][i]\n k -= (1 << i)\n return node \n``` | 59 | You are given a tree with `n` nodes numbered from `0` to `n - 1` in the form of a parent array `parent` where `parent[i]` is the parent of `ith` node. The root of the tree is node `0`. Find the `kth` ancestor of a given node.
The `kth` ancestor of a tree node is the `kth` node in the path from that node to the root node.
Implement the `TreeAncestor` class:
* `TreeAncestor(int n, int[] parent)` Initializes the object with the number of nodes in the tree and the parent array.
* `int getKthAncestor(int node, int k)` return the `kth` ancestor of the given node `node`. If there is no such ancestor, return `-1`.
**Example 1:**
**Input**
\[ "TreeAncestor ", "getKthAncestor ", "getKthAncestor ", "getKthAncestor "\]
\[\[7, \[-1, 0, 0, 1, 1, 2, 2\]\], \[3, 1\], \[5, 2\], \[6, 3\]\]
**Output**
\[null, 1, 0, -1\]
**Explanation**
TreeAncestor treeAncestor = new TreeAncestor(7, \[-1, 0, 0, 1, 1, 2, 2\]);
treeAncestor.getKthAncestor(3, 1); // returns 1 which is the parent of 3
treeAncestor.getKthAncestor(5, 2); // returns 0 which is the grandparent of 5
treeAncestor.getKthAncestor(6, 3); // returns -1 because there is no such ancestor
**Constraints:**
* `1 <= k <= n <= 5 * 104`
* `parent.length == n`
* `parent[0] == -1`
* `0 <= parent[i] < n` for all `0 < i < n`
* `0 <= node < n`
* There will be at most `5 * 104` queries. | Build array rank where rank[i][j] is the number of votes for team i to be the j-th rank. Sort the trams by rank array. if rank array is the same for two or more teams, sort them by the ID in ascending order. |
[Python3] binary lifting (dp) | kth-ancestor-of-a-tree-node | 0 | 1 | Algo\nFor node 0, 1, ..., n-1, we define a matrix `self.dp[][]` whose `i, j`th element indicates the `i`th node\'s `2^j` parent. Here, `i = 0, 1, ..., n-1` and `j = 0, 1, ..., int(log2(n))`. An important recursive relationship is that \n\n`self.dp[i][j] = self.dp[self.dp[i][j-1]][j-1]`. \n\nIn other words, `i`th node\'s `2^j` parent is `i`th node\'s `2^(j-1)` parent\'s `2^(j-1)` parent. In this way, lookup is guarenteed to complete in `O(logN)` time. Note that it takes `O(NlogN)` to build `self.dp`. \n\nTime complexity `O(NlogN)` to pre-processing the tree and `O(logN)` for each equery thereafter. \n```\nclass TreeAncestor:\n\n def __init__(self, n: int, parent: List[int]):\n m = 1 + int(log2(n)) #at most 16 for this problem \n self.dp = [[-1] * m for _ in range(n)] #ith node\'s 2^j parent\n for j in range(m):\n for i in range(n):\n if j == 0: self.dp[i][0] = parent[i] #2^0 parent\n elif self.dp[i][j-1] != -1: \n self.dp[i][j] = self.dp[self.dp[i][j-1]][j-1]\n \n def getKthAncestor(self, node: int, k: int) -> int:\n while k > 0 and node != -1: \n i = int(log2(k))\n node = self.dp[node][i]\n k -= (1 << i)\n return node \n``` | 59 | Given an array of integers `nums` and a positive integer `k`, check whether it is possible to divide this array into sets of `k` consecutive numbers.
Return `true` _if it is possible_. Otherwise, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,3,4,4,5,6\], k = 4
**Output:** true
**Explanation:** Array can be divided into \[1,2,3,4\] and \[3,4,5,6\].
**Example 2:**
**Input:** nums = \[3,2,1,2,3,4,3,4,5,9,10,11\], k = 3
**Output:** true
**Explanation:** Array can be divided into \[1,2,3\] , \[2,3,4\] , \[3,4,5\] and \[9,10,11\].
**Example 3:**
**Input:** nums = \[1,2,3,4\], k = 3
**Output:** false
**Explanation:** Each array should be divided in subarrays of size 3.
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `1 <= nums[i] <= 109`
**Note:** This question is the same as 846: [https://leetcode.com/problems/hand-of-straights/](https://leetcode.com/problems/hand-of-straights/) | The queries must be answered efficiently to avoid time limit exceeded verdict. Use sparse table (dynamic programming application) to travel the tree upwards in a fast way. |
python code | kth-ancestor-of-a-tree-node | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe can solve this question through precomputation of the ansestor if we will precomputate all the ansestors of all the node then time complextiy and space complextiy will be O(n^2). But we could do one thing as we know that we can write any number as a sum of power of 2 also known as binary presentation. so we can precomputate the 2^kth (0<=k<=log(n)+1) ansestor of each node. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nI created a 2d array P. P[i][j] denotes 2^(i) ansestor of j th node.\nlets say we have to 5 the ansestor of node j then we can say that \n5=4+1 so \'\'\'5th ansestor of j is 4th ansestor of 1st ansestor of j\'\'\'\nor \'\'\'5th ansestor of j is 1st ansestor of 4th ansestor of j\'\'\'\n Creation of p array;\n-As we know that (2^i)+(2^i)=2^(i+1) so if we know the 2^ith ansestor of all the node we can find 2^(i+1)th ansestor of any index j by finding 2^ith ansestor of 2^ith ansestor of j. so p[i][j]=p[i-1][p[i-1][j]] but if 2^ith ansestor of j is -1 so 2^(i+1)th ansestor of j will be also -1 (which means no ansestor) i have deal with this -1 case by taking minimun of (0,p[i-1][j]) because if 2^ith ansestor of j will be -1 then 2^ith ansestor of 0 will be also -1 and their will be no error in our code . Note here we know 2^0th ansestor of each node given in the question. so will start from 1 to log(n)\n calculation of k th ansestor\ni have just created a variable ans and initialized it with node\n\'O\' is the current last set bit \nthen we change ans with oth ansestor of ans\nthen subtract o from k. ans so on till k becomes 0 or ans becomes -1.\n\n# Complexity\n- Time complexity: O(nlog(n)) for precumputation and O(log(n)) for each query\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(nlog(n))\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom math import log\nclass TreeAncestor:\n p=[]\n def __init__(self, n: int, parent: List[int]):\n self.p=[[0]*n for r in range(int(n**(0.5))+1)]\n self.p[0]=parent[:]\n # print(self.p)\n for i in range(1,int(n**(0.5))+1):\n for j in range(n):\n self.p[i][j]=self.p[i-1][max(0,self.p[i-1][j])]\n # print(self.p)\n def getKthAncestor(self, node: int, k: int) -> int:\n ans=node\n while k>0 and ans!=-1:\n o=k&-k\n ans=self.p[int(log(o,2))][ans]\n # print(o,k,ans)\n k-=o\n return ans\n\n\n# Your TreeAncestor object will be instantiated and called as such:\n# obj = TreeAncestor(n, parent)\n# param_1 = obj.getKthAncestor(node,k)\n``` | 1 | You are given a tree with `n` nodes numbered from `0` to `n - 1` in the form of a parent array `parent` where `parent[i]` is the parent of `ith` node. The root of the tree is node `0`. Find the `kth` ancestor of a given node.
The `kth` ancestor of a tree node is the `kth` node in the path from that node to the root node.
Implement the `TreeAncestor` class:
* `TreeAncestor(int n, int[] parent)` Initializes the object with the number of nodes in the tree and the parent array.
* `int getKthAncestor(int node, int k)` return the `kth` ancestor of the given node `node`. If there is no such ancestor, return `-1`.
**Example 1:**
**Input**
\[ "TreeAncestor ", "getKthAncestor ", "getKthAncestor ", "getKthAncestor "\]
\[\[7, \[-1, 0, 0, 1, 1, 2, 2\]\], \[3, 1\], \[5, 2\], \[6, 3\]\]
**Output**
\[null, 1, 0, -1\]
**Explanation**
TreeAncestor treeAncestor = new TreeAncestor(7, \[-1, 0, 0, 1, 1, 2, 2\]);
treeAncestor.getKthAncestor(3, 1); // returns 1 which is the parent of 3
treeAncestor.getKthAncestor(5, 2); // returns 0 which is the grandparent of 5
treeAncestor.getKthAncestor(6, 3); // returns -1 because there is no such ancestor
**Constraints:**
* `1 <= k <= n <= 5 * 104`
* `parent.length == n`
* `parent[0] == -1`
* `0 <= parent[i] < n` for all `0 < i < n`
* `0 <= node < n`
* There will be at most `5 * 104` queries. | Build array rank where rank[i][j] is the number of votes for team i to be the j-th rank. Sort the trams by rank array. if rank array is the same for two or more teams, sort them by the ID in ascending order. |
python code | kth-ancestor-of-a-tree-node | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe can solve this question through precomputation of the ansestor if we will precomputate all the ansestors of all the node then time complextiy and space complextiy will be O(n^2). But we could do one thing as we know that we can write any number as a sum of power of 2 also known as binary presentation. so we can precomputate the 2^kth (0<=k<=log(n)+1) ansestor of each node. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nI created a 2d array P. P[i][j] denotes 2^(i) ansestor of j th node.\nlets say we have to 5 the ansestor of node j then we can say that \n5=4+1 so \'\'\'5th ansestor of j is 4th ansestor of 1st ansestor of j\'\'\'\nor \'\'\'5th ansestor of j is 1st ansestor of 4th ansestor of j\'\'\'\n Creation of p array;\n-As we know that (2^i)+(2^i)=2^(i+1) so if we know the 2^ith ansestor of all the node we can find 2^(i+1)th ansestor of any index j by finding 2^ith ansestor of 2^ith ansestor of j. so p[i][j]=p[i-1][p[i-1][j]] but if 2^ith ansestor of j is -1 so 2^(i+1)th ansestor of j will be also -1 (which means no ansestor) i have deal with this -1 case by taking minimun of (0,p[i-1][j]) because if 2^ith ansestor of j will be -1 then 2^ith ansestor of 0 will be also -1 and their will be no error in our code . Note here we know 2^0th ansestor of each node given in the question. so will start from 1 to log(n)\n calculation of k th ansestor\ni have just created a variable ans and initialized it with node\n\'O\' is the current last set bit \nthen we change ans with oth ansestor of ans\nthen subtract o from k. ans so on till k becomes 0 or ans becomes -1.\n\n# Complexity\n- Time complexity: O(nlog(n)) for precumputation and O(log(n)) for each query\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(nlog(n))\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom math import log\nclass TreeAncestor:\n p=[]\n def __init__(self, n: int, parent: List[int]):\n self.p=[[0]*n for r in range(int(n**(0.5))+1)]\n self.p[0]=parent[:]\n # print(self.p)\n for i in range(1,int(n**(0.5))+1):\n for j in range(n):\n self.p[i][j]=self.p[i-1][max(0,self.p[i-1][j])]\n # print(self.p)\n def getKthAncestor(self, node: int, k: int) -> int:\n ans=node\n while k>0 and ans!=-1:\n o=k&-k\n ans=self.p[int(log(o,2))][ans]\n # print(o,k,ans)\n k-=o\n return ans\n\n\n# Your TreeAncestor object will be instantiated and called as such:\n# obj = TreeAncestor(n, parent)\n# param_1 = obj.getKthAncestor(node,k)\n``` | 1 | Given an array of integers `nums` and a positive integer `k`, check whether it is possible to divide this array into sets of `k` consecutive numbers.
Return `true` _if it is possible_. Otherwise, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,3,4,4,5,6\], k = 4
**Output:** true
**Explanation:** Array can be divided into \[1,2,3,4\] and \[3,4,5,6\].
**Example 2:**
**Input:** nums = \[3,2,1,2,3,4,3,4,5,9,10,11\], k = 3
**Output:** true
**Explanation:** Array can be divided into \[1,2,3\] , \[2,3,4\] , \[3,4,5\] and \[9,10,11\].
**Example 3:**
**Input:** nums = \[1,2,3,4\], k = 3
**Output:** false
**Explanation:** Each array should be divided in subarrays of size 3.
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `1 <= nums[i] <= 109`
**Note:** This question is the same as 846: [https://leetcode.com/problems/hand-of-straights/](https://leetcode.com/problems/hand-of-straights/) | The queries must be answered efficiently to avoid time limit exceeded verdict. Use sparse table (dynamic programming application) to travel the tree upwards in a fast way. |
[Python] Binary lifting with simple explanation | kth-ancestor-of-a-tree-node | 0 | 1 | \nFor each node, we can calculate the parent of the parent of the node (parent2) by \n```python\nparent2 = parent[parent[node]].\n```\nSimilary, we can calculate parent4 by calculating \n```python\nparent4 = parent2[parent2[node]]\n ```\nTherefore we can caculate parent 2^(k+1) of node v by parent 2^k of node v.\n (k,v) denotes parent 2^k of node v.\n```python\n lift[k+1, v]=lift[k, lift[k, v]]\n ```\n \nSolution\n```python\nclass TreeAncestor:\n\n def __init__(self, n: int, parent: List[int]):\n self.lift = collections.defaultdict(int)\n for i in range(n):\n self.lift[0, i] = parent[i]\n \n for k in range(16):\n for v in range(n):\n if self.lift[k,v] < 0:\n self.lift[k+1,v] = -1 # inefficient \n else:\n self.lift[k+1,v]=self.lift[k,self.lift[k,v]]\n \n def getKthAncestor(self, node: int, k: int) -> int:\n if k==0:\n return node\n if node == -1:\n return node\n dps = int(math.log2(k))\n k -= pow(2, dps)\n return self.getKthAncestor(self.lift[dps,node], k)\n```\n\n## About the following part:\n```python\ndps = int(math.log2(k))\nk -= pow(2, dps)\n```\nFor example, if k == 18 then math.log2(18) = 4. This means 2^4 = 16 and this is the largest number which is a exponent of 2 and less than 18.\n```\nk -= pow(2, 4) # -> k = 4\n```\nSince k=4 is a exponent of 2, the answer is already stored in self.lift.\n\n## About the complexity of the alogirithm:\n```\ndps = int(math.log2(k))\n```\nThis dps is the largest exponent of 2 which is smaller than or equal to k. Therefore 2^dps <=k and k < 2^(dps+1). \n Therefore the following inequlity:\n```\nk/2 < 2^dps <=k\n```\nholds.\nBy the following update\n ```\n k -= pow(2, dps)\n```\nk is reduced by 2^dps, which is greater than k/2.\n\n | 10 | You are given a tree with `n` nodes numbered from `0` to `n - 1` in the form of a parent array `parent` where `parent[i]` is the parent of `ith` node. The root of the tree is node `0`. Find the `kth` ancestor of a given node.
The `kth` ancestor of a tree node is the `kth` node in the path from that node to the root node.
Implement the `TreeAncestor` class:
* `TreeAncestor(int n, int[] parent)` Initializes the object with the number of nodes in the tree and the parent array.
* `int getKthAncestor(int node, int k)` return the `kth` ancestor of the given node `node`. If there is no such ancestor, return `-1`.
**Example 1:**
**Input**
\[ "TreeAncestor ", "getKthAncestor ", "getKthAncestor ", "getKthAncestor "\]
\[\[7, \[-1, 0, 0, 1, 1, 2, 2\]\], \[3, 1\], \[5, 2\], \[6, 3\]\]
**Output**
\[null, 1, 0, -1\]
**Explanation**
TreeAncestor treeAncestor = new TreeAncestor(7, \[-1, 0, 0, 1, 1, 2, 2\]);
treeAncestor.getKthAncestor(3, 1); // returns 1 which is the parent of 3
treeAncestor.getKthAncestor(5, 2); // returns 0 which is the grandparent of 5
treeAncestor.getKthAncestor(6, 3); // returns -1 because there is no such ancestor
**Constraints:**
* `1 <= k <= n <= 5 * 104`
* `parent.length == n`
* `parent[0] == -1`
* `0 <= parent[i] < n` for all `0 < i < n`
* `0 <= node < n`
* There will be at most `5 * 104` queries. | Build array rank where rank[i][j] is the number of votes for team i to be the j-th rank. Sort the trams by rank array. if rank array is the same for two or more teams, sort them by the ID in ascending order. |
[Python] Binary lifting with simple explanation | kth-ancestor-of-a-tree-node | 0 | 1 | \nFor each node, we can calculate the parent of the parent of the node (parent2) by \n```python\nparent2 = parent[parent[node]].\n```\nSimilary, we can calculate parent4 by calculating \n```python\nparent4 = parent2[parent2[node]]\n ```\nTherefore we can caculate parent 2^(k+1) of node v by parent 2^k of node v.\n (k,v) denotes parent 2^k of node v.\n```python\n lift[k+1, v]=lift[k, lift[k, v]]\n ```\n \nSolution\n```python\nclass TreeAncestor:\n\n def __init__(self, n: int, parent: List[int]):\n self.lift = collections.defaultdict(int)\n for i in range(n):\n self.lift[0, i] = parent[i]\n \n for k in range(16):\n for v in range(n):\n if self.lift[k,v] < 0:\n self.lift[k+1,v] = -1 # inefficient \n else:\n self.lift[k+1,v]=self.lift[k,self.lift[k,v]]\n \n def getKthAncestor(self, node: int, k: int) -> int:\n if k==0:\n return node\n if node == -1:\n return node\n dps = int(math.log2(k))\n k -= pow(2, dps)\n return self.getKthAncestor(self.lift[dps,node], k)\n```\n\n## About the following part:\n```python\ndps = int(math.log2(k))\nk -= pow(2, dps)\n```\nFor example, if k == 18 then math.log2(18) = 4. This means 2^4 = 16 and this is the largest number which is a exponent of 2 and less than 18.\n```\nk -= pow(2, 4) # -> k = 4\n```\nSince k=4 is a exponent of 2, the answer is already stored in self.lift.\n\n## About the complexity of the alogirithm:\n```\ndps = int(math.log2(k))\n```\nThis dps is the largest exponent of 2 which is smaller than or equal to k. Therefore 2^dps <=k and k < 2^(dps+1). \n Therefore the following inequlity:\n```\nk/2 < 2^dps <=k\n```\nholds.\nBy the following update\n ```\n k -= pow(2, dps)\n```\nk is reduced by 2^dps, which is greater than k/2.\n\n | 10 | Given an array of integers `nums` and a positive integer `k`, check whether it is possible to divide this array into sets of `k` consecutive numbers.
Return `true` _if it is possible_. Otherwise, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,3,4,4,5,6\], k = 4
**Output:** true
**Explanation:** Array can be divided into \[1,2,3,4\] and \[3,4,5,6\].
**Example 2:**
**Input:** nums = \[3,2,1,2,3,4,3,4,5,9,10,11\], k = 3
**Output:** true
**Explanation:** Array can be divided into \[1,2,3\] , \[2,3,4\] , \[3,4,5\] and \[9,10,11\].
**Example 3:**
**Input:** nums = \[1,2,3,4\], k = 3
**Output:** false
**Explanation:** Each array should be divided in subarrays of size 3.
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `1 <= nums[i] <= 109`
**Note:** This question is the same as 846: [https://leetcode.com/problems/hand-of-straights/](https://leetcode.com/problems/hand-of-straights/) | The queries must be answered efficiently to avoid time limit exceeded verdict. Use sparse table (dynamic programming application) to travel the tree upwards in a fast way. |
Simple Python Binary Lifting | kth-ancestor-of-a-tree-node | 1 | 1 | \tclass TreeAncestor:\n\n\t\tdef __init__(self, n: int, parent: List[int]):\n\t\t\tself.mx = int(log2(n))+1\n\t\t\tself.table = [[-1 for _ in range(n)] for i in range(self.mx)]\n\t\t\tfor i in range(n):\n\t\t\t\tself.table[0][i]=parent[i]\n\t\t\tfor i in range(1,self.mx):\n\t\t\t\tfor j in range(n):\n\t\t\t\t\tif self.table[i-1][j]!=-1:\n\t\t\t\t\t\tself.table[i][j]=self.table[i-1][self.table[i-1][j]]\n\n\t\tdef getKthAncestor(self, node: int, k: int) -> int:\n\t\t\tfor i in range(self.mx+1):\n\t\t\t\tmask = 1<<i\n\t\t\t\tif mask&k:\n\t\t\t\t\tnode=self.table[i][node]\n\t\t\t\t\tif node==-1:\n\t\t\t\t\t\tbreak\n\t\t\treturn node\n\n\n\t# Your TreeAncestor object will be instantiated and called as such:\n\t# obj = TreeAncestor(n, parent)\n\t# param_1 = obj.getKthAncestor(node,k) | 2 | You are given a tree with `n` nodes numbered from `0` to `n - 1` in the form of a parent array `parent` where `parent[i]` is the parent of `ith` node. The root of the tree is node `0`. Find the `kth` ancestor of a given node.
The `kth` ancestor of a tree node is the `kth` node in the path from that node to the root node.
Implement the `TreeAncestor` class:
* `TreeAncestor(int n, int[] parent)` Initializes the object with the number of nodes in the tree and the parent array.
* `int getKthAncestor(int node, int k)` return the `kth` ancestor of the given node `node`. If there is no such ancestor, return `-1`.
**Example 1:**
**Input**
\[ "TreeAncestor ", "getKthAncestor ", "getKthAncestor ", "getKthAncestor "\]
\[\[7, \[-1, 0, 0, 1, 1, 2, 2\]\], \[3, 1\], \[5, 2\], \[6, 3\]\]
**Output**
\[null, 1, 0, -1\]
**Explanation**
TreeAncestor treeAncestor = new TreeAncestor(7, \[-1, 0, 0, 1, 1, 2, 2\]);
treeAncestor.getKthAncestor(3, 1); // returns 1 which is the parent of 3
treeAncestor.getKthAncestor(5, 2); // returns 0 which is the grandparent of 5
treeAncestor.getKthAncestor(6, 3); // returns -1 because there is no such ancestor
**Constraints:**
* `1 <= k <= n <= 5 * 104`
* `parent.length == n`
* `parent[0] == -1`
* `0 <= parent[i] < n` for all `0 < i < n`
* `0 <= node < n`
* There will be at most `5 * 104` queries. | Build array rank where rank[i][j] is the number of votes for team i to be the j-th rank. Sort the trams by rank array. if rank array is the same for two or more teams, sort them by the ID in ascending order. |
Simple Python Binary Lifting | kth-ancestor-of-a-tree-node | 1 | 1 | \tclass TreeAncestor:\n\n\t\tdef __init__(self, n: int, parent: List[int]):\n\t\t\tself.mx = int(log2(n))+1\n\t\t\tself.table = [[-1 for _ in range(n)] for i in range(self.mx)]\n\t\t\tfor i in range(n):\n\t\t\t\tself.table[0][i]=parent[i]\n\t\t\tfor i in range(1,self.mx):\n\t\t\t\tfor j in range(n):\n\t\t\t\t\tif self.table[i-1][j]!=-1:\n\t\t\t\t\t\tself.table[i][j]=self.table[i-1][self.table[i-1][j]]\n\n\t\tdef getKthAncestor(self, node: int, k: int) -> int:\n\t\t\tfor i in range(self.mx+1):\n\t\t\t\tmask = 1<<i\n\t\t\t\tif mask&k:\n\t\t\t\t\tnode=self.table[i][node]\n\t\t\t\t\tif node==-1:\n\t\t\t\t\t\tbreak\n\t\t\treturn node\n\n\n\t# Your TreeAncestor object will be instantiated and called as such:\n\t# obj = TreeAncestor(n, parent)\n\t# param_1 = obj.getKthAncestor(node,k) | 2 | Given an array of integers `nums` and a positive integer `k`, check whether it is possible to divide this array into sets of `k` consecutive numbers.
Return `true` _if it is possible_. Otherwise, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,3,4,4,5,6\], k = 4
**Output:** true
**Explanation:** Array can be divided into \[1,2,3,4\] and \[3,4,5,6\].
**Example 2:**
**Input:** nums = \[3,2,1,2,3,4,3,4,5,9,10,11\], k = 3
**Output:** true
**Explanation:** Array can be divided into \[1,2,3\] , \[2,3,4\] , \[3,4,5\] and \[9,10,11\].
**Example 3:**
**Input:** nums = \[1,2,3,4\], k = 3
**Output:** false
**Explanation:** Each array should be divided in subarrays of size 3.
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `1 <= nums[i] <= 109`
**Note:** This question is the same as 846: [https://leetcode.com/problems/hand-of-straights/](https://leetcode.com/problems/hand-of-straights/) | The queries must be answered efficiently to avoid time limit exceeded verdict. Use sparse table (dynamic programming application) to travel the tree upwards in a fast way. |
Very simple python solution, faster than 99%, O(1) query time complexity | kth-ancestor-of-a-tree-node | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass TreeAncestor:\n\n def __init__(self, n: int, parent: List[int]):\n n = len(parent)\n existing = set(parent)\n self.cache = {} \n for node in range(n):\n if node not in existing:\n key = node\n self.cache[key] = []\n level = 0\n while node != -1:\n self.cache[key].append(parent[node])\n self.cache[parent[node]] = (key, level + 1)\n node = parent[node]\n level += 1\n\n def getKthAncestor(self, node: int, k: int) -> int:\n if k == 0:\n return node\n result = self.cache[node] \n if not isinstance(result, list):\n node, level = result\n k += level\n return self.cache[node][k - 1] if k <= len(self.cache[node]) else -1\n \n \n\n\n# Your TreeAncestor object will be instantiated and called as such:\n# obj = TreeAncestor(n, parent)\n# param_1 = obj.getKthAncestor(node,k)\n\n``` | 0 | You are given a tree with `n` nodes numbered from `0` to `n - 1` in the form of a parent array `parent` where `parent[i]` is the parent of `ith` node. The root of the tree is node `0`. Find the `kth` ancestor of a given node.
The `kth` ancestor of a tree node is the `kth` node in the path from that node to the root node.
Implement the `TreeAncestor` class:
* `TreeAncestor(int n, int[] parent)` Initializes the object with the number of nodes in the tree and the parent array.
* `int getKthAncestor(int node, int k)` return the `kth` ancestor of the given node `node`. If there is no such ancestor, return `-1`.
**Example 1:**
**Input**
\[ "TreeAncestor ", "getKthAncestor ", "getKthAncestor ", "getKthAncestor "\]
\[\[7, \[-1, 0, 0, 1, 1, 2, 2\]\], \[3, 1\], \[5, 2\], \[6, 3\]\]
**Output**
\[null, 1, 0, -1\]
**Explanation**
TreeAncestor treeAncestor = new TreeAncestor(7, \[-1, 0, 0, 1, 1, 2, 2\]);
treeAncestor.getKthAncestor(3, 1); // returns 1 which is the parent of 3
treeAncestor.getKthAncestor(5, 2); // returns 0 which is the grandparent of 5
treeAncestor.getKthAncestor(6, 3); // returns -1 because there is no such ancestor
**Constraints:**
* `1 <= k <= n <= 5 * 104`
* `parent.length == n`
* `parent[0] == -1`
* `0 <= parent[i] < n` for all `0 < i < n`
* `0 <= node < n`
* There will be at most `5 * 104` queries. | Build array rank where rank[i][j] is the number of votes for team i to be the j-th rank. Sort the trams by rank array. if rank array is the same for two or more teams, sort them by the ID in ascending order. |
Very simple python solution, faster than 99%, O(1) query time complexity | kth-ancestor-of-a-tree-node | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass TreeAncestor:\n\n def __init__(self, n: int, parent: List[int]):\n n = len(parent)\n existing = set(parent)\n self.cache = {} \n for node in range(n):\n if node not in existing:\n key = node\n self.cache[key] = []\n level = 0\n while node != -1:\n self.cache[key].append(parent[node])\n self.cache[parent[node]] = (key, level + 1)\n node = parent[node]\n level += 1\n\n def getKthAncestor(self, node: int, k: int) -> int:\n if k == 0:\n return node\n result = self.cache[node] \n if not isinstance(result, list):\n node, level = result\n k += level\n return self.cache[node][k - 1] if k <= len(self.cache[node]) else -1\n \n \n\n\n# Your TreeAncestor object will be instantiated and called as such:\n# obj = TreeAncestor(n, parent)\n# param_1 = obj.getKthAncestor(node,k)\n\n``` | 0 | Given an array of integers `nums` and a positive integer `k`, check whether it is possible to divide this array into sets of `k` consecutive numbers.
Return `true` _if it is possible_. Otherwise, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,3,4,4,5,6\], k = 4
**Output:** true
**Explanation:** Array can be divided into \[1,2,3,4\] and \[3,4,5,6\].
**Example 2:**
**Input:** nums = \[3,2,1,2,3,4,3,4,5,9,10,11\], k = 3
**Output:** true
**Explanation:** Array can be divided into \[1,2,3\] , \[2,3,4\] , \[3,4,5\] and \[9,10,11\].
**Example 3:**
**Input:** nums = \[1,2,3,4\], k = 3
**Output:** false
**Explanation:** Each array should be divided in subarrays of size 3.
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `1 <= nums[i] <= 109`
**Note:** This question is the same as 846: [https://leetcode.com/problems/hand-of-straights/](https://leetcode.com/problems/hand-of-straights/) | The queries must be answered efficiently to avoid time limit exceeded verdict. Use sparse table (dynamic programming application) to travel the tree upwards in a fast way. |
Clean and Simple intuitive solution in python | kth-ancestor-of-a-tree-node | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. --> Preprocess the tree by keeping 2,4,8,16,32... ancesstor for each node. after that given any query we can reach there by using binary number property in log(n) time. \n\nFor example, if we need to find 6th ancesstor of node A, we can find the 4th ancesstor of node A which is B . Now we\'ll check for the 2nd ancesstor of node B which will eventually give me 6th ancesstor of node A.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(nlogn)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass TreeAncestor:\n\n def __init__(self, n: int, parent: List[int]):\n self.dp= [[-1 for _ in range(16)] for _ in range(n+1)]\n self.parent= parent\n for j in range(16):\n for i in range(n):\n if j==0:\n self.dp[i][j]= self.parent[i]\n else:\n self.dp[i][j]= self.dp[self.dp[i][j-1]][j-1]\n\n def getKthAncestor(self, x: int, k: int) -> int:\n for j in range(16):\n if (k&(1<<j)):\n x= self.dp[x][j]\n return x\n\n\n# Your TreeAncestor object will be instantiated and called as such:\n# obj = TreeAncestor(n, parent)\n# param_1 = obj.getKthAncestor(node,k)\n``` | 0 | You are given a tree with `n` nodes numbered from `0` to `n - 1` in the form of a parent array `parent` where `parent[i]` is the parent of `ith` node. The root of the tree is node `0`. Find the `kth` ancestor of a given node.
The `kth` ancestor of a tree node is the `kth` node in the path from that node to the root node.
Implement the `TreeAncestor` class:
* `TreeAncestor(int n, int[] parent)` Initializes the object with the number of nodes in the tree and the parent array.
* `int getKthAncestor(int node, int k)` return the `kth` ancestor of the given node `node`. If there is no such ancestor, return `-1`.
**Example 1:**
**Input**
\[ "TreeAncestor ", "getKthAncestor ", "getKthAncestor ", "getKthAncestor "\]
\[\[7, \[-1, 0, 0, 1, 1, 2, 2\]\], \[3, 1\], \[5, 2\], \[6, 3\]\]
**Output**
\[null, 1, 0, -1\]
**Explanation**
TreeAncestor treeAncestor = new TreeAncestor(7, \[-1, 0, 0, 1, 1, 2, 2\]);
treeAncestor.getKthAncestor(3, 1); // returns 1 which is the parent of 3
treeAncestor.getKthAncestor(5, 2); // returns 0 which is the grandparent of 5
treeAncestor.getKthAncestor(6, 3); // returns -1 because there is no such ancestor
**Constraints:**
* `1 <= k <= n <= 5 * 104`
* `parent.length == n`
* `parent[0] == -1`
* `0 <= parent[i] < n` for all `0 < i < n`
* `0 <= node < n`
* There will be at most `5 * 104` queries. | Build array rank where rank[i][j] is the number of votes for team i to be the j-th rank. Sort the trams by rank array. if rank array is the same for two or more teams, sort them by the ID in ascending order. |
Clean and Simple intuitive solution in python | kth-ancestor-of-a-tree-node | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. --> Preprocess the tree by keeping 2,4,8,16,32... ancesstor for each node. after that given any query we can reach there by using binary number property in log(n) time. \n\nFor example, if we need to find 6th ancesstor of node A, we can find the 4th ancesstor of node A which is B . Now we\'ll check for the 2nd ancesstor of node B which will eventually give me 6th ancesstor of node A.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(nlogn)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass TreeAncestor:\n\n def __init__(self, n: int, parent: List[int]):\n self.dp= [[-1 for _ in range(16)] for _ in range(n+1)]\n self.parent= parent\n for j in range(16):\n for i in range(n):\n if j==0:\n self.dp[i][j]= self.parent[i]\n else:\n self.dp[i][j]= self.dp[self.dp[i][j-1]][j-1]\n\n def getKthAncestor(self, x: int, k: int) -> int:\n for j in range(16):\n if (k&(1<<j)):\n x= self.dp[x][j]\n return x\n\n\n# Your TreeAncestor object will be instantiated and called as such:\n# obj = TreeAncestor(n, parent)\n# param_1 = obj.getKthAncestor(node,k)\n``` | 0 | Given an array of integers `nums` and a positive integer `k`, check whether it is possible to divide this array into sets of `k` consecutive numbers.
Return `true` _if it is possible_. Otherwise, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,3,4,4,5,6\], k = 4
**Output:** true
**Explanation:** Array can be divided into \[1,2,3,4\] and \[3,4,5,6\].
**Example 2:**
**Input:** nums = \[3,2,1,2,3,4,3,4,5,9,10,11\], k = 3
**Output:** true
**Explanation:** Array can be divided into \[1,2,3\] , \[2,3,4\] , \[3,4,5\] and \[9,10,11\].
**Example 3:**
**Input:** nums = \[1,2,3,4\], k = 3
**Output:** false
**Explanation:** Each array should be divided in subarrays of size 3.
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `1 <= nums[i] <= 109`
**Note:** This question is the same as 846: [https://leetcode.com/problems/hand-of-straights/](https://leetcode.com/problems/hand-of-straights/) | The queries must be answered efficiently to avoid time limit exceeded verdict. Use sparse table (dynamic programming application) to travel the tree upwards in a fast way. |
Pandas vs SQL | Elegant & Short | All 30 Days of Pandas solutions ✅ | group-sold-products-by-the-date | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```Python []\ndef categorize_products(activities: pd.DataFrame) -> pd.DataFrame:\n return activities.groupby(\n \'sell_date\'\n )[\'product\'].agg([\n (\'num_sold\', \'nunique\'),\n (\'products\', lambda x: \',\'.join(sorted(x.unique())))\n ]).reset_index()\n```\n```SQL []\nSELECT sell_date,\n count(DISTINCT product) AS num_sold,\n group_concat(DISTINCT product ORDER BY product ASC SEPARATOR \',\') products\n FROM activities\n GROUP BY sell_date\n ORDER BY sell_date;\n```\n\n# Important!\n###### If you like the solution or find it useful, feel free to **upvote** for it, it will support me in creating high quality solutions)\n\n# 30 Days of Pandas solutions\n\n### Data Filtering \u2705\n- [Big Countries](https://leetcode.com/problems/big-countries/solutions/3848474/pandas-elegant-short-1-line/)\n- [Recyclable and Low Fat Products](https://leetcode.com/problems/recyclable-and-low-fat-products/solutions/3848500/pandas-elegant-short-1-line/)\n- [Customers Who Never Order](https://leetcode.com/problems/customers-who-never-order/solutions/3848527/pandas-elegant-short-1-line/)\n- [Article Views I](https://leetcode.com/problems/article-views-i/solutions/3867192/pandas-elegant-short-1-line/)\n\n\n### String Methods \u2705\n- [Invalid Tweets](https://leetcode.com/problems/invalid-tweets/solutions/3849121/pandas-elegant-short-1-line/)\n- [Calculate Special Bonus](https://leetcode.com/problems/calculate-special-bonus/solutions/3867209/pandas-elegant-short-1-line/)\n- [Fix Names in a Table](https://leetcode.com/problems/fix-names-in-a-table/solutions/3849167/pandas-elegant-short-1-line/)\n- [Find Users With Valid E-Mails](https://leetcode.com/problems/find-users-with-valid-e-mails/solutions/3849177/pandas-elegant-short-1-line/)\n- [Patients With a Condition](https://leetcode.com/problems/patients-with-a-condition/solutions/3849196/pandas-elegant-short-1-line-regex/)\n\n\n### Data Manipulation \u2705\n- [Nth Highest Salary](https://leetcode.com/problems/nth-highest-salary/solutions/3867257/pandas-elegant-short-1-line/)\n- [Second Highest Salary](https://leetcode.com/problems/second-highest-salary/solutions/3867278/pandas-elegant-short/)\n- [Department Highest Salary](https://leetcode.com/problems/department-highest-salary/solutions/3867312/pandas-elegant-short-1-line/)\n- [Rank Scores](https://leetcode.com/problems/rank-scores/solutions/3872817/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Delete Duplicate Emails](https://leetcode.com/problems/delete-duplicate-emails/solutions/3849211/pandas-elegant-short/)\n- [Rearrange Products Table](https://leetcode.com/problems/rearrange-products-table/solutions/3849226/pandas-elegant-short-1-line/)\n\n\n### Statistics \u2705\n- [The Number of Rich Customers](https://leetcode.com/problems/the-number-of-rich-customers/solutions/3849251/pandas-elegant-short-1-line/)\n- [Immediate Food Delivery I](https://leetcode.com/problems/immediate-food-delivery-i/solutions/3872719/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Count Salary Categories](https://leetcode.com/problems/count-salary-categories/solutions/3872801/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n\n### Data Aggregation \u2705\n- [Find Total Time Spent by Each Employee](https://leetcode.com/problems/find-total-time-spent-by-each-employee/solutions/3872715/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Game Play Analysis I](https://leetcode.com/problems/game-play-analysis-i/solutions/3863223/pandas-elegant-short-1-line/)\n- [Number of Unique Subjects Taught by Each Teacher](https://leetcode.com/problems/number-of-unique-subjects-taught-by-each-teacher/solutions/3863239/pandas-elegant-short-1-line/)\n- [Classes More Than 5 Students](https://leetcode.com/problems/classes-more-than-5-students/solutions/3863249/pandas-elegant-short/)\n- [Customer Placing the Largest Number of Orders](https://leetcode.com/problems/customer-placing-the-largest-number-of-orders/solutions/3863257/pandas-elegant-short-1-line/)\n- [Group Sold Products By The Date](https://leetcode.com/problems/group-sold-products-by-the-date/solutions/3863267/pandas-elegant-short-1-line/)\n- [Daily Leads and Partners](https://leetcode.com/problems/daily-leads-and-partners/solutions/3863279/pandas-elegant-short-1-line/)\n\n\n### Data Aggregation \u2705\n- [Actors and Directors Who Cooperated At Least Three Times](https://leetcode.com/problems/actors-and-directors-who-cooperated-at-least-three-times/solutions/3863309/pandas-elegant-short/)\n- [Replace Employee ID With The Unique Identifier](https://leetcode.com/problems/replace-employee-id-with-the-unique-identifier/solutions/3872822/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Students and Examinations](https://leetcode.com/problems/students-and-examinations/solutions/3872699/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Managers with at Least 5 Direct Reports](https://leetcode.com/problems/managers-with-at-least-5-direct-reports/solutions/3872861/pandas-elegant-short/)\n- [Sales Person](https://leetcode.com/problems/sales-person/solutions/3872712/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n | 62 | You are given a string `s` of **even length** consisting of digits from `0` to `9`, and two integers `a` and `b`.
You can apply either of the following two operations any number of times and in any order on `s`:
* Add `a` to all odd indices of `s` **(0-indexed)**. Digits post `9` are cycled back to `0`. For example, if `s = "3456 "` and `a = 5`, `s` becomes `"3951 "`.
* Rotate `s` to the right by `b` positions. For example, if `s = "3456 "` and `b = 1`, `s` becomes `"6345 "`.
Return _the **lexicographically smallest** string you can obtain by applying the above operations any number of times on_ `s`.
A string `a` is lexicographically smaller than a string `b` (of the same length) if in the first position where `a` and `b` differ, string `a` has a letter that appears earlier in the alphabet than the corresponding letter in `b`. For example, `"0158 "` is lexicographically smaller than `"0190 "` because the first position they differ is at the third letter, and `'5'` comes before `'9'`.
**Example 1:**
**Input:** s = "5525 ", a = 9, b = 2
**Output:** "2050 "
**Explanation:** We can apply the following operations:
Start: "5525 "
Rotate: "2555 "
Add: "2454 "
Add: "2353 "
Rotate: "5323 "
Add: "5222 "
Add: "5121 "
Rotate: "2151 "
Add: "2050 "
There is no way to obtain a string that is lexicographically smaller then "2050 ".
**Example 2:**
**Input:** s = "74 ", a = 5, b = 1
**Output:** "24 "
**Explanation:** We can apply the following operations:
Start: "74 "
Rotate: "47 "
Add: "42 "
Rotate: "24 "
There is no way to obtain a string that is lexicographically smaller then "24 ".
**Example 3:**
**Input:** s = "0011 ", a = 4, b = 2
**Output:** "0011 "
**Explanation:** There are no sequence of operations that will give us a lexicographically smaller string than "0011 ".
**Constraints:**
* `2 <= s.length <= 100`
* `s.length` is even.
* `s` consists of digits from `0` to `9` only.
* `1 <= a <= 9`
* `1 <= b <= s.length - 1` | null |
Grouping With Aggregations 🏆 | group-sold-products-by-the-date | 0 | 1 | # My SQL\n\nFirst, we group the data by the `sell_date` column. This allows us to count the number of unique products sold on each sell date, which we store in the `num_sold` column.\n\nThe most challenging part is to sort and join all unique product names in each group to get the products column. We can use the `GROUP_CONCAT()` function to combine multiple values from multiple rows into a single string. The syntax of the `GROUP_CONCAT()` function is as follows:\n```\nGROUP_CONCAT(DISTINCT [column_name] [separator])\n```\nThe `DISTINCT` keyword ensures that only unique values are concatenated. The separator parameter specifies the character that should be used to separate the values.\n\n``` sql []\n# Write your MySQL query statement below\nSELECT sell_date, COUNT(DISTINCT(product)) as num_sold,\nGROUP_CONCAT(\n DISTINCT product \n ORDER BY product \n SEPARATOR \',\'\n) AS products\nFROM Activities\nGROUP BY sell_date\nORDER BY sell_date ASC\n```\n\n# Pandas\n\nThe question asks us to group and summarize data by date. To do this, we first use the `groupby` function to group the `DataFrame` activities by date. This creates a new object called `groups`, which is a `DataFrameGroupBy` object.\n\nOnce we have the `DataFrameGroupBy` object, we can use the `agg()` function to perform aggregation operations on each group. The `agg()` function takes a list of aggregation tasks to perform. In this case, we are specifying two aggregation tasks:\n- Creating num_solid column with the number of unique products sold on each sell date. \n`num_sold=(\'product\', \'nunique\')`\n- Join all unique names within each group. \n`products=(\'product\', lambda x: \',\'.join(sorted(set(x))))`\n\n``` python3 []\nimport pandas as pd\n\ndef categorize_products(activities: pd.DataFrame) -> pd.DataFrame:\n groups = activities.groupby(\'sell_date\')\n\n stats = groups.agg(\n num_sold=(\'product\', \'nunique\'),\n products=(\'product\', lambda x: \',\'.join(sorted(set(x))))\n ).reset_index()\n stats.sort_values(\'sell_date\', inplace=True)\n return stats\n``` | 7 | You are given a string `s` of **even length** consisting of digits from `0` to `9`, and two integers `a` and `b`.
You can apply either of the following two operations any number of times and in any order on `s`:
* Add `a` to all odd indices of `s` **(0-indexed)**. Digits post `9` are cycled back to `0`. For example, if `s = "3456 "` and `a = 5`, `s` becomes `"3951 "`.
* Rotate `s` to the right by `b` positions. For example, if `s = "3456 "` and `b = 1`, `s` becomes `"6345 "`.
Return _the **lexicographically smallest** string you can obtain by applying the above operations any number of times on_ `s`.
A string `a` is lexicographically smaller than a string `b` (of the same length) if in the first position where `a` and `b` differ, string `a` has a letter that appears earlier in the alphabet than the corresponding letter in `b`. For example, `"0158 "` is lexicographically smaller than `"0190 "` because the first position they differ is at the third letter, and `'5'` comes before `'9'`.
**Example 1:**
**Input:** s = "5525 ", a = 9, b = 2
**Output:** "2050 "
**Explanation:** We can apply the following operations:
Start: "5525 "
Rotate: "2555 "
Add: "2454 "
Add: "2353 "
Rotate: "5323 "
Add: "5222 "
Add: "5121 "
Rotate: "2151 "
Add: "2050 "
There is no way to obtain a string that is lexicographically smaller then "2050 ".
**Example 2:**
**Input:** s = "74 ", a = 5, b = 1
**Output:** "24 "
**Explanation:** We can apply the following operations:
Start: "74 "
Rotate: "47 "
Add: "42 "
Rotate: "24 "
There is no way to obtain a string that is lexicographically smaller then "24 ".
**Example 3:**
**Input:** s = "0011 ", a = 4, b = 2
**Output:** "0011 "
**Explanation:** There are no sequence of operations that will give us a lexicographically smaller string than "0011 ".
**Constraints:**
* `2 <= s.length <= 100`
* `s.length` is even.
* `s` consists of digits from `0` to `9` only.
* `1 <= a <= 9`
* `1 <= b <= s.length - 1` | null |
xor-operation-in-an-array | xor-operation-in-an-array | 0 | 1 | # Code\n```\nclass Solution:\n def xorOperation(self, n: int, start: int) -> int:\n l = [start]\n count = start\n for i in range(1,n):\n l.append(start + 2*i)\n count^= l[-1]\n return count\n \n``` | 1 | You are given an integer `n` and an integer `start`.
Define an array `nums` where `nums[i] = start + 2 * i` (**0-indexed**) and `n == nums.length`.
Return _the bitwise XOR of all elements of_ `nums`.
**Example 1:**
**Input:** n = 5, start = 0
**Output:** 8
**Explanation:** Array nums is equal to \[0, 2, 4, 6, 8\] where (0 ^ 2 ^ 4 ^ 6 ^ 8) = 8.
Where "^ " corresponds to bitwise XOR operator.
**Example 2:**
**Input:** n = 4, start = 3
**Output:** 8
**Explanation:** Array nums is equal to \[3, 5, 7, 9\] where (3 ^ 5 ^ 7 ^ 9) = 8.
**Constraints:**
* `1 <= n <= 1000`
* `0 <= start <= 1000`
* `n == nums.length` | Sort 'arr2' and use binary search to get the closest element for each 'arr1[i]', it gives a time complexity of O(nlogn). |
xor-operation-in-an-array | xor-operation-in-an-array | 0 | 1 | # Code\n```\nclass Solution:\n def xorOperation(self, n: int, start: int) -> int:\n l = [start]\n count = start\n for i in range(1,n):\n l.append(start + 2*i)\n count^= l[-1]\n return count\n \n``` | 1 | You are given an array `points`, an integer `angle`, and your `location`, where `location = [posx, posy]` and `points[i] = [xi, yi]` both denote **integral coordinates** on the X-Y plane.
Initially, you are facing directly east from your position. You **cannot move** from your position, but you can **rotate**. In other words, `posx` and `posy` cannot be changed. Your field of view in **degrees** is represented by `angle`, determining how wide you can see from any given view direction. Let `d` be the amount in degrees that you rotate counterclockwise. Then, your field of view is the **inclusive** range of angles `[d - angle/2, d + angle/2]`.
Your browser does not support the video tag or this video format.
You can **see** some set of points if, for each point, the **angle** formed by the point, your position, and the immediate east direction from your position is **in your field of view**.
There can be multiple points at one coordinate. There may be points at your location, and you can always see these points regardless of your rotation. Points do not obstruct your vision to other points.
Return _the maximum number of points you can see_.
**Example 1:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,3\]\], angle = 90, location = \[1,1\]
**Output:** 3
**Explanation:** The shaded region represents your field of view. All points can be made visible in your field of view, including \[3,3\] even though \[2,2\] is in front and in the same line of sight.
**Example 2:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,4\],\[1,1\]\], angle = 90, location = \[1,1\]
**Output:** 4
**Explanation:** All points can be made visible in your field of view, including the one at your location.
**Example 3:**
**Input:** points = \[\[1,0\],\[2,1\]\], angle = 13, location = \[1,1\]
**Output:** 1
**Explanation:** You can only see one of the two points, as shown above.
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `location.length == 2`
* `0 <= angle < 360`
* `0 <= posx, posy, xi, yi <= 100` | Simulate the process, create an array nums and return the Bitwise XOR of all elements of it. |
Python || Simple Solution || Beginner Friendly | xor-operation-in-an-array | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def xorOperation(self, n: int, start: int) -> int:\n xor = 0\n for i in range(n):\n xor = xor ^ start\n start+=2\n return xor\n``` | 3 | You are given an integer `n` and an integer `start`.
Define an array `nums` where `nums[i] = start + 2 * i` (**0-indexed**) and `n == nums.length`.
Return _the bitwise XOR of all elements of_ `nums`.
**Example 1:**
**Input:** n = 5, start = 0
**Output:** 8
**Explanation:** Array nums is equal to \[0, 2, 4, 6, 8\] where (0 ^ 2 ^ 4 ^ 6 ^ 8) = 8.
Where "^ " corresponds to bitwise XOR operator.
**Example 2:**
**Input:** n = 4, start = 3
**Output:** 8
**Explanation:** Array nums is equal to \[3, 5, 7, 9\] where (3 ^ 5 ^ 7 ^ 9) = 8.
**Constraints:**
* `1 <= n <= 1000`
* `0 <= start <= 1000`
* `n == nums.length` | Sort 'arr2' and use binary search to get the closest element for each 'arr1[i]', it gives a time complexity of O(nlogn). |
Python || Simple Solution || Beginner Friendly | xor-operation-in-an-array | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def xorOperation(self, n: int, start: int) -> int:\n xor = 0\n for i in range(n):\n xor = xor ^ start\n start+=2\n return xor\n``` | 3 | You are given an array `points`, an integer `angle`, and your `location`, where `location = [posx, posy]` and `points[i] = [xi, yi]` both denote **integral coordinates** on the X-Y plane.
Initially, you are facing directly east from your position. You **cannot move** from your position, but you can **rotate**. In other words, `posx` and `posy` cannot be changed. Your field of view in **degrees** is represented by `angle`, determining how wide you can see from any given view direction. Let `d` be the amount in degrees that you rotate counterclockwise. Then, your field of view is the **inclusive** range of angles `[d - angle/2, d + angle/2]`.
Your browser does not support the video tag or this video format.
You can **see** some set of points if, for each point, the **angle** formed by the point, your position, and the immediate east direction from your position is **in your field of view**.
There can be multiple points at one coordinate. There may be points at your location, and you can always see these points regardless of your rotation. Points do not obstruct your vision to other points.
Return _the maximum number of points you can see_.
**Example 1:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,3\]\], angle = 90, location = \[1,1\]
**Output:** 3
**Explanation:** The shaded region represents your field of view. All points can be made visible in your field of view, including \[3,3\] even though \[2,2\] is in front and in the same line of sight.
**Example 2:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,4\],\[1,1\]\], angle = 90, location = \[1,1\]
**Output:** 4
**Explanation:** All points can be made visible in your field of view, including the one at your location.
**Example 3:**
**Input:** points = \[\[1,0\],\[2,1\]\], angle = 13, location = \[1,1\]
**Output:** 1
**Explanation:** You can only see one of the two points, as shown above.
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `location.length == 2`
* `0 <= angle < 360`
* `0 <= posx, posy, xi, yi <= 100` | Simulate the process, create an array nums and return the Bitwise XOR of all elements of it. |
✅✔ SIMPLE PYTHON3 SOLUTION ✅✔ easiest code | xor-operation-in-an-array | 0 | 1 | ***UPVOTE*** if it is helpful\n``` \nclass Solution:\n def xorOperation(self, n: int, start: int) -> int:\n ans = 0\n for i in range(n):\n ans ^= start\n start+=2\n return ans\n``` | 2 | You are given an integer `n` and an integer `start`.
Define an array `nums` where `nums[i] = start + 2 * i` (**0-indexed**) and `n == nums.length`.
Return _the bitwise XOR of all elements of_ `nums`.
**Example 1:**
**Input:** n = 5, start = 0
**Output:** 8
**Explanation:** Array nums is equal to \[0, 2, 4, 6, 8\] where (0 ^ 2 ^ 4 ^ 6 ^ 8) = 8.
Where "^ " corresponds to bitwise XOR operator.
**Example 2:**
**Input:** n = 4, start = 3
**Output:** 8
**Explanation:** Array nums is equal to \[3, 5, 7, 9\] where (3 ^ 5 ^ 7 ^ 9) = 8.
**Constraints:**
* `1 <= n <= 1000`
* `0 <= start <= 1000`
* `n == nums.length` | Sort 'arr2' and use binary search to get the closest element for each 'arr1[i]', it gives a time complexity of O(nlogn). |
✅✔ SIMPLE PYTHON3 SOLUTION ✅✔ easiest code | xor-operation-in-an-array | 0 | 1 | ***UPVOTE*** if it is helpful\n``` \nclass Solution:\n def xorOperation(self, n: int, start: int) -> int:\n ans = 0\n for i in range(n):\n ans ^= start\n start+=2\n return ans\n``` | 2 | You are given an array `points`, an integer `angle`, and your `location`, where `location = [posx, posy]` and `points[i] = [xi, yi]` both denote **integral coordinates** on the X-Y plane.
Initially, you are facing directly east from your position. You **cannot move** from your position, but you can **rotate**. In other words, `posx` and `posy` cannot be changed. Your field of view in **degrees** is represented by `angle`, determining how wide you can see from any given view direction. Let `d` be the amount in degrees that you rotate counterclockwise. Then, your field of view is the **inclusive** range of angles `[d - angle/2, d + angle/2]`.
Your browser does not support the video tag or this video format.
You can **see** some set of points if, for each point, the **angle** formed by the point, your position, and the immediate east direction from your position is **in your field of view**.
There can be multiple points at one coordinate. There may be points at your location, and you can always see these points regardless of your rotation. Points do not obstruct your vision to other points.
Return _the maximum number of points you can see_.
**Example 1:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,3\]\], angle = 90, location = \[1,1\]
**Output:** 3
**Explanation:** The shaded region represents your field of view. All points can be made visible in your field of view, including \[3,3\] even though \[2,2\] is in front and in the same line of sight.
**Example 2:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,4\],\[1,1\]\], angle = 90, location = \[1,1\]
**Output:** 4
**Explanation:** All points can be made visible in your field of view, including the one at your location.
**Example 3:**
**Input:** points = \[\[1,0\],\[2,1\]\], angle = 13, location = \[1,1\]
**Output:** 1
**Explanation:** You can only see one of the two points, as shown above.
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `location.length == 2`
* `0 <= angle < 360`
* `0 <= posx, posy, xi, yi <= 100` | Simulate the process, create an array nums and return the Bitwise XOR of all elements of it. |
[Python] Simple Solution | xor-operation-in-an-array | 0 | 1 | ```\nclass Solution:\n def xorOperation(self, n: int, start: int) -> int:\n ## RC ##\n ## APPROACH : MATH ##\n res = 0\n for i in range(n):\n res ^= start + 2 * i\n return res\n``` | 23 | You are given an integer `n` and an integer `start`.
Define an array `nums` where `nums[i] = start + 2 * i` (**0-indexed**) and `n == nums.length`.
Return _the bitwise XOR of all elements of_ `nums`.
**Example 1:**
**Input:** n = 5, start = 0
**Output:** 8
**Explanation:** Array nums is equal to \[0, 2, 4, 6, 8\] where (0 ^ 2 ^ 4 ^ 6 ^ 8) = 8.
Where "^ " corresponds to bitwise XOR operator.
**Example 2:**
**Input:** n = 4, start = 3
**Output:** 8
**Explanation:** Array nums is equal to \[3, 5, 7, 9\] where (3 ^ 5 ^ 7 ^ 9) = 8.
**Constraints:**
* `1 <= n <= 1000`
* `0 <= start <= 1000`
* `n == nums.length` | Sort 'arr2' and use binary search to get the closest element for each 'arr1[i]', it gives a time complexity of O(nlogn). |
[Python] Simple Solution | xor-operation-in-an-array | 0 | 1 | ```\nclass Solution:\n def xorOperation(self, n: int, start: int) -> int:\n ## RC ##\n ## APPROACH : MATH ##\n res = 0\n for i in range(n):\n res ^= start + 2 * i\n return res\n``` | 23 | You are given an array `points`, an integer `angle`, and your `location`, where `location = [posx, posy]` and `points[i] = [xi, yi]` both denote **integral coordinates** on the X-Y plane.
Initially, you are facing directly east from your position. You **cannot move** from your position, but you can **rotate**. In other words, `posx` and `posy` cannot be changed. Your field of view in **degrees** is represented by `angle`, determining how wide you can see from any given view direction. Let `d` be the amount in degrees that you rotate counterclockwise. Then, your field of view is the **inclusive** range of angles `[d - angle/2, d + angle/2]`.
Your browser does not support the video tag or this video format.
You can **see** some set of points if, for each point, the **angle** formed by the point, your position, and the immediate east direction from your position is **in your field of view**.
There can be multiple points at one coordinate. There may be points at your location, and you can always see these points regardless of your rotation. Points do not obstruct your vision to other points.
Return _the maximum number of points you can see_.
**Example 1:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,3\]\], angle = 90, location = \[1,1\]
**Output:** 3
**Explanation:** The shaded region represents your field of view. All points can be made visible in your field of view, including \[3,3\] even though \[2,2\] is in front and in the same line of sight.
**Example 2:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,4\],\[1,1\]\], angle = 90, location = \[1,1\]
**Output:** 4
**Explanation:** All points can be made visible in your field of view, including the one at your location.
**Example 3:**
**Input:** points = \[\[1,0\],\[2,1\]\], angle = 13, location = \[1,1\]
**Output:** 1
**Explanation:** You can only see one of the two points, as shown above.
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `location.length == 2`
* `0 <= angle < 360`
* `0 <= posx, posy, xi, yi <= 100` | Simulate the process, create an array nums and return the Bitwise XOR of all elements of it. |
Python3 || Beats 94.67% | xor-operation-in-an-array | 0 | 1 | \n\n\n# Code\n```\nclass Solution:\n def xorOperation(self, n: int, start: int) -> int:\n s1=[]\n r = 0\n for i in range(n):\n s=start+(i*2)\n s1.append(s)\n for i in range(len(s1)):\n r = r ^ s1[i]\n return r\n \n``` | 3 | You are given an integer `n` and an integer `start`.
Define an array `nums` where `nums[i] = start + 2 * i` (**0-indexed**) and `n == nums.length`.
Return _the bitwise XOR of all elements of_ `nums`.
**Example 1:**
**Input:** n = 5, start = 0
**Output:** 8
**Explanation:** Array nums is equal to \[0, 2, 4, 6, 8\] where (0 ^ 2 ^ 4 ^ 6 ^ 8) = 8.
Where "^ " corresponds to bitwise XOR operator.
**Example 2:**
**Input:** n = 4, start = 3
**Output:** 8
**Explanation:** Array nums is equal to \[3, 5, 7, 9\] where (3 ^ 5 ^ 7 ^ 9) = 8.
**Constraints:**
* `1 <= n <= 1000`
* `0 <= start <= 1000`
* `n == nums.length` | Sort 'arr2' and use binary search to get the closest element for each 'arr1[i]', it gives a time complexity of O(nlogn). |
Python3 || Beats 94.67% | xor-operation-in-an-array | 0 | 1 | \n\n\n# Code\n```\nclass Solution:\n def xorOperation(self, n: int, start: int) -> int:\n s1=[]\n r = 0\n for i in range(n):\n s=start+(i*2)\n s1.append(s)\n for i in range(len(s1)):\n r = r ^ s1[i]\n return r\n \n``` | 3 | You are given an array `points`, an integer `angle`, and your `location`, where `location = [posx, posy]` and `points[i] = [xi, yi]` both denote **integral coordinates** on the X-Y plane.
Initially, you are facing directly east from your position. You **cannot move** from your position, but you can **rotate**. In other words, `posx` and `posy` cannot be changed. Your field of view in **degrees** is represented by `angle`, determining how wide you can see from any given view direction. Let `d` be the amount in degrees that you rotate counterclockwise. Then, your field of view is the **inclusive** range of angles `[d - angle/2, d + angle/2]`.
Your browser does not support the video tag or this video format.
You can **see** some set of points if, for each point, the **angle** formed by the point, your position, and the immediate east direction from your position is **in your field of view**.
There can be multiple points at one coordinate. There may be points at your location, and you can always see these points regardless of your rotation. Points do not obstruct your vision to other points.
Return _the maximum number of points you can see_.
**Example 1:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,3\]\], angle = 90, location = \[1,1\]
**Output:** 3
**Explanation:** The shaded region represents your field of view. All points can be made visible in your field of view, including \[3,3\] even though \[2,2\] is in front and in the same line of sight.
**Example 2:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,4\],\[1,1\]\], angle = 90, location = \[1,1\]
**Output:** 4
**Explanation:** All points can be made visible in your field of view, including the one at your location.
**Example 3:**
**Input:** points = \[\[1,0\],\[2,1\]\], angle = 13, location = \[1,1\]
**Output:** 1
**Explanation:** You can only see one of the two points, as shown above.
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `location.length == 2`
* `0 <= angle < 360`
* `0 <= posx, posy, xi, yi <= 100` | Simulate the process, create an array nums and return the Bitwise XOR of all elements of it. |
Simple Python Solution | xor-operation-in-an-array | 0 | 1 | Time Complexcity O(N)\nSpace Complexcity O(1)\n```\nclass Solution:\n def xorOperation(self, n: int, start: int) -> int:\n re=start\n for i in range(1,n):\n ne=start+2*i\n re^=ne\n return re\n``` | 1 | You are given an integer `n` and an integer `start`.
Define an array `nums` where `nums[i] = start + 2 * i` (**0-indexed**) and `n == nums.length`.
Return _the bitwise XOR of all elements of_ `nums`.
**Example 1:**
**Input:** n = 5, start = 0
**Output:** 8
**Explanation:** Array nums is equal to \[0, 2, 4, 6, 8\] where (0 ^ 2 ^ 4 ^ 6 ^ 8) = 8.
Where "^ " corresponds to bitwise XOR operator.
**Example 2:**
**Input:** n = 4, start = 3
**Output:** 8
**Explanation:** Array nums is equal to \[3, 5, 7, 9\] where (3 ^ 5 ^ 7 ^ 9) = 8.
**Constraints:**
* `1 <= n <= 1000`
* `0 <= start <= 1000`
* `n == nums.length` | Sort 'arr2' and use binary search to get the closest element for each 'arr1[i]', it gives a time complexity of O(nlogn). |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.