filename
stringlengths 7
140
| content
stringlengths 0
76.7M
|
|---|---|
code/computational_geometry/src/2d_line_intersection/2d_line_intersection.js | // computational geometry | 2D line intersecton | JavaScript
function intersection_by_points(x1, y1, x2, y2, x3, y3, x4, y4) {
var x12 = x1 - x2;
var x34 = x3 - x4;
var y12 = y1 - y2;
var y34 = y3 - y4;
var c = x12 * y34 - y12 * x34;
var a = x1 * y2 - y1 * x2;
var b = x3 * y4 - y3 * x4;
var x = (a * x34 - b * x12) / c;
var y = (a * y34 - b * y12) / c;
// Keeping points integers. Change according to requirement
x = parseInt(x);
y = parseInt(y);
return { x: x, y: y };
}
// Line segments defined by 2 points a-b and c-d
function intersection_by_vectors(vec1, vec2, vec3, vec4) {
return intersection_by_points(
vec1["x"],
vec1["y"],
vec2["x"],
vec2["y"],
vec3["x"],
vec3["y"],
vec4["x"],
vec4["y"]
);
}
// Accepts line in Ax+By = C format
function intersection_by_line_euqation(line1, line2) {
var A1 = line1["A"];
var B1 = line1["B"];
var C1 = line1["C"];
var A2 = line2["A"];
var B2 = line2["B"];
var C2 = line2["C"];
var delta = A1 * B2 - A2 * B1;
if (delta === 0) console.log("Lines are parallel");
var x = (B2 * C1 - B1 * C2) / delta;
var y = (A1 * C2 - A2 * C1) / delta;
// Keeping points integers. Change according to requirement
x = parseInt(x);
y = parseInt(y);
return { x: x, y: y };
}
// Driver Program
function main() {
// 3x + 4y = 1
var line1 = { A: 3, B: 4, C: 1 };
// 2x + 5y = 3
var line2 = { A: 2, B: 5, C: 3 };
var intersection_point = intersection_by_line_euqation(line1, line2);
console.log("Test using line equation");
console.log(
`Lines intersect at x:${intersection_point["x"]}, y:${
intersection_point["y"]
}`
);
console.log("Test using points");
intersection_point = intersection_by_vectors(
{ x: 2, y: 5 },
{ x: 5, y: 3 },
{ x: 7, y: 4 },
{ x: 1, y: 6 }
);
console.log(
`Lines intersect at x:${intersection_point["x"]}, y:${
intersection_point["y"]
}`
);
}
main();
|
code/computational_geometry/src/2d_line_intersection/2d_line_intersection.py | # computational geometry | 2D line intersecton | Python
def parallel_int(verticeX, verticeY):
k = (verticeY[2] - verticeY[0]) * (verticeX[1] - verticeX[0]) - (
verticeX[2] - verticeX[0]
) * (verticeY[1] - verticeY[0])
if k == 0:
return "infinite"
else:
return "no"
def line_int(verticeX, verticeY):
x12 = verticeX[0] - verticeX[1]
x34 = verticeX[2] - verticeX[3]
y12 = verticeY[0] - verticeY[1]
y34 = verticeY[2] - verticeY[3]
c = x12 * y34 - y12 * x34
if c == 0:
return ("NoInt", None)
a = verticeX[0] * verticeY[1] - verticeY[0] * verticeX[1]
b = verticeX[2] * verticeY[3] - verticeY[2] * verticeX[3]
x = (a * x34 - b * x12) / c
y = (a * y34 - b * y12) / c
return (x, y)
X = []
Y = []
try:
input = raw_input
except NameError:
pass
print("Enter 2-point form of each line")
X.append(float(input("X of point 1, line 1: ")))
Y.append(float(input("Y of point 1, line 1: ")))
X.append(float(input("X of point 2, line 1: ")))
Y.append(float(input("Y of point 2, line 1: ")))
X.append(float(input("X of point 1, line 2: ")))
Y.append(float(input("Y of point 1, line 2: ")))
X.append(float(input("X of point 2, line 2: ")))
Y.append(float(input("Y of point 2, line 2: ")))
intersectn = line_int(X, Y)
if intersectn[0] == "NoInt":
print("Parallel lines found with " + parallel_int(X, Y) + " intersections")
else:
print(
"Point of intersection : ("
+ str(intersectn[0])
+ ", "
+ str(intersectn[1])
+ ")"
)
|
code/computational_geometry/src/2d_line_intersection/2d_line_intersection.rb | class LineInterserction
def initialize(x1, y1, x2, y2, x3, y3, x4, y4)
@x1 = x1
@x2 = x2
@x3 = x3
@y1 = y1
@y2 = y2
@y3 = y3
@x4 = x4
@y4 = y4
@denom = ((@x1 - @x2) * (@y3 - @y4)) - ((@y1 - @y2) * (@x3 - @x4))
end
def is_parallel
@denom == 0
end
def intersection_point
p1 = ((@x1 * @y2 - @y1 * @x2) * (@x3 - @x4) - (@x1 - @x2) * (@x3 * @y4 - @y3 * @x4)) / @denom
p2 = ((@x1 * @y2 - @y1 * @x2) * (@y3 - @y4) - (@y1 - @y2) * (@x3 * @y4 - @y3 * @x4)) / @denom
"#{p1},#{p2}"
end
end
obj = LineInterserction.new(10, 3, 20, 3, 10, 5, 20, 5) #=> Cordinate points (x1,y1,x2,y2,x3,y3,x4,y4)
if obj.is_parallel == false
puts "Intersection Point: #{obj.intersection_point}"
else
puts "Line Parallel : #{obj.is_parallel}"
end
|
code/computational_geometry/src/2d_line_intersection/README.md | # cosmos
Your personal library of every algorithm and data structure code that you will ever encounter
## 2 Dimensional line intersection
This package contains programs for 2D line intersections.
The program checks if two lines are `parallel` or `intersecting`. If they intersect, it gives the point of intersection.
<p align="center">
A massive collaborative effort by <a href="https://github.com/OpenGenus/cosmos">OpenGenus Foundation</a>
</p> |
code/computational_geometry/src/2d_line_intersection/line_determinant_method.cpp | #include <iostream>
class TwoDimensionalLineIntersection
{
public:
bool determinantMethod();
void setCoordinatesOfLines(double x1_, double y1_, double x2_, double y2_, double x3_, double y3_, double x4_, double y4_);
void printIntersectionPoints();
private:
double x1_, y1_, x2_, y2_, x3_, y3_, x4_, y4_, xin_, yin_;
};
void TwoDimensionalLineIntersection :: setCoordinatesOfLines(double x1_, double y1_, double x2_, double y2_, double x3_,
double y3_, double x4_, double y4_)
{
this->x1_ = x1_;
this->x2_ = x2_;
this->x3_ = x3_;
this->x4_ = x4_;
this->y1_ = y1_;
this->y2_ = y2_;
this->y3_ = y3_;
this->y4_ = y4_;
}
bool TwoDimensionalLineIntersection :: determinantMethod()
{
double slopeOfLine1;
double slopeOfLine2;
if(x2_ - x1_ != 0)
slopeOfLine1 = (y2_ - y1_)/(x2_ - x1_);
else
slopeOfLine1 = 0;
if(x4_ - x3_ != 0)
slopeOfLine2 = (y4_ - y3_)/(x4_ - x3_);
else
slopeOfLine1 = 0;
if(slopeOfLine1 != slopeOfLine2)
{
xin_ = ((x1_*y2_ - y1_*x2_)*(x3_ - x4_) - (x3_*y4_ - y3_*x4_)*(x1_ - x2_) )/( ((x1_ - x2_)*(y3_ - y4_))- ((y1_ - y2_)*(x3_ - x4_)));
yin_ = ((x1_*y2_ - y1_*x2_)*(y3_ - y4_) - (x3_*y4_ - y3_*x4_)*(y1_ - y2_) )/( ((x1_ - x2_)*(y3_ - y4_))- ((y1_ - y2_)*(x3_ - x4_)));
return true;
} else
return false;
}
void TwoDimensionalLineIntersection ::printIntersectionPoints()
{
if(determinantMethod())
{
std::cout << "\nIntersection Coordinate : ";
std::cout << "\nX-coordinate : " << xin_;
std::cout << "\nY-coordinate : " << yin_;
} else
std::cout << "\nLines are Parallel.";
}
int main()
{
TwoDimensionalLineIntersection t;
double x1, y1, x2, y2, x3, y3, x4, y4;
std::cout << "\nEnter the Coordinates for Line-1 : ";
std::cout << "\nLine-1 | x1-coordinate : ";
std::cin >> x1;
std::cout << "\nLine-1 | y1-coordinate : ";
std::cin >> y1;
std::cout << "\nLine-1 | x2-coordinate : ";
std::cin >> x2;
std::cout << "\nLine-1 | y2-coordinate : ";
std::cin >> y2;
std::cout << "\nEnter the Coordinates for Line-2 : ";
std::cout << "\nLine-2 | x3-coordinate : ";
std::cin >> x3;
std::cout << "\nLine-2 | y3-coordinate : ";
std::cin >> y3;
std::cout << "\nLine-2 | x4-coordinate : ";
std::cin >> x4;
std::cout << "\nLine-2 | y4-coordinate : ";
std::cin >> y4;
t.setCoordinatesOfLines(x1, y1, x2, y2, x3, y3, x4, y4);
t.printIntersectionPoints();
}
|
code/computational_geometry/src/2d_line_intersection/line_elemination_method.cpp | #include <iostream>
#include <vector>
class EliminationMethd2DLineIntersection
{
public:
void acceptTheCoordinates(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4);
void intersection1(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4);
private:
std::vector<double> a, b, c, d; //four coordinates constituting 2 Dimensional Lines.
};
void EliminationMethd2DLineIntersection::acceptTheCoordinates(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4)
{
a.push_back(x1);
a.push_back(y1);
b.push_back(x1);
b.push_back(y1);
c.push_back(x1);
c.push_back(y1);
d.push_back(x1);
d.push_back(y1);
intersection1(a[0], a[1], b[0], b[1], c[0], c[1], d[0], d[1]);
}
void EliminationMethd2DLineIntersection::intersection1(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4)
{
double x12 = x1 - x2;
double x34 = x3 - x4;
double y12 = y1 - y2;
double y34 = y3 - y4;
double c = x12 * y34 - y12 * x34;
double a = x1 * y2 - y1 * x2;
double b = x3 * y4 - y3 * x4;
if(c != 0)
{
double x = (a * x34 - b * x12) / c;
double y = (a * y34 - b * y12) / c;
std::cout << "Intersection point coordinates : \n";
std::cout << "Xin : " << x << std::endl;
std::cout << "Yin : " << y << std::endl;
}
else
{
std::cout << "Lines are parallel";
}
}
int main()
{
EliminationMethd2DLineIntersection obj;
int value;
double x1, y1, x2, y2, x3, y3, x4, y4, x5, y5, x6, y6, x7, y7, x8, y8;
std::cout << "\nEnter the Coordinates for Line-1";
std::cout << "\nEnter the X-coordinate for Point-1: ";
std::cin >> x1;
std::cout << "\nEnter the Y-coordinate for Point-1: ";
std::cin >> y1;
std::cout << "\nEnter the X-coordinate for Point-2: ";
std::cin >> x2;
std::cout << "\nEnter the Y-coordinate for Point-2: ";
std::cin >> y2;
std::cout << "\nEnter the Coordinates for Line-2";
std::cout << "\nEnter the X-coordinate for Point-1: ";
std::cin >> x3;
std::cout << "\nEnter the Y-coordinate for Point-1: ";
std::cin >> y3;
std::cout << "\nEnter the X-coordinate for Point-2: ";
std::cin >> x4;
std::cout << "\nEnter the Y-coordinate for Point-2: ";
std::cin >> y4;
obj.acceptTheCoordinates(x1,y1, x2, y2, x3, y3, x4, y4);
return 0;
}
|
code/computational_geometry/src/2d_separating_axis_test/2d_separating_axis_test.cpp | // computational geometry | Two convex polygon intersection 2d seperating axis test | C++
//Ivan Reinaldo Liyanto
// open genus - cosmos
#include <cmath>
#include <iostream>
#include <vector>
using namespace std;
struct vec2
{
double x, y;
vec2(double x, double y) : x(x), y(y)
{
}
friend vec2 operator+(vec2 lhs, const vec2& vec)
{
return vec2(lhs.x + vec.x, lhs.y + vec.y);
}
friend vec2 operator-(vec2 lhs, const vec2& vec)
{
return vec2(lhs.x - vec.x, lhs.y - vec.y);
}
};
double dot(vec2 a, vec2 b)
{
return a.x * b.x + a.y * b.y;
}
vector<vec2> inputPolygon1;
vector<vec2> inputPolygon2;
bool sat()
{
//project every points onto every axis
for (size_t i = 1; i < inputPolygon1.size(); i++)
{
vec2 axis = inputPolygon1[i] - inputPolygon1[i - 1];
double leftMostPolygonA = __FLT_MAX__;
double rightMostPolygonA = __FLT_MIN__;
for (size_t j = 0; j < inputPolygon1.size(); j++)
{
double d = dot(inputPolygon1[j], axis);
if (d > rightMostPolygonA)
rightMostPolygonA = d;
if (d < leftMostPolygonA)
leftMostPolygonA = d;
}
double leftMostPolygonB = __FLT_MAX__;
double rightMostPolygonB = __FLT_MIN__;
for (size_t j = 0; j < inputPolygon2.size(); j++)
{
double d = dot(inputPolygon2[j], axis);
if (d > rightMostPolygonB)
rightMostPolygonB = d;
if (d < leftMostPolygonB)
leftMostPolygonB = d;
}
if ((leftMostPolygonB < rightMostPolygonA && rightMostPolygonB > rightMostPolygonA) ||
(leftMostPolygonA < rightMostPolygonB && rightMostPolygonA > rightMostPolygonB) )
return true;
}
//false = no intersection
return false;
}
int main()
{
//given 2 convex polygons defined by set of points, determine if the two polygon intersects using Separating Axis Test
//example set 1
inputPolygon1.push_back(vec2(5, 5));
inputPolygon1.push_back(vec2(7, 10));
inputPolygon1.push_back(vec2(15, 10));
inputPolygon1.push_back(vec2(4, 4));
inputPolygon2.push_back(vec2(6, 6));
inputPolygon2.push_back(vec2(0, 0));
inputPolygon2.push_back(vec2(7, 0));
cout << "The two polygons " << (sat() ? "" : "do not ") << "intersect\n";
return 0;
}
|
code/computational_geometry/src/README.md | # cosmos
> Your personal library of every algorithm and data structure code that you will ever encounter
Computational geometry is a branch of computer science devoted to the study of algorithms which can be formulated in geometric terms. While modern computational geometry is a recent development, it is one of the oldest fields of computing with history stretching back to antiquity.
The primary goal of research in combinatorial computational geometry is to develop efficient algorithms and data structures for solving problems stated in terms of basic geometrical objects: points, line segments, polygons, polyhedra, etc.
---
<p align="center">
A massive collaborative effort by <a href="https://github.com/OpenGenus/cosmos">OpenGenus Foundation</a>
</p>
---
|
code/computational_geometry/src/area_of_polygon/area_of_polygon.c | /* computational geometry | area of polygon | C
* @Author: Ayush Garg
* @Date: 2017-10-13 01:20:26
* @Last Modified by: Ayush Garg
* @Last Modified time: 2017-10-13 01:31:03
* Part of Cosmos by OpenGenus Foundation
*/
#include <stdio.h>
typedef struct
{
double x, y;
} point;
double calcArea(point a, point b, point c)
{
double tmp = ((a.x - b.x) * (c.y - b.y) - (a.y - b.y) * (c.x - b.x)) / 2;
return (tmp < 0) ? (-tmp) : tmp;
}
int main()
{
double ans = 0;
int n;
printf("Enter number of vertices \n");
scanf("%d", &n);
point points[n];
for (int i = 0; i < n; i++)
{
scanf("%lf %lf", &points[i].x, &points[i].y);
}
for (int i = 2; i < n; i++)
{
ans += calcArea(points[0], points[i - 1], points[i]);
}
printf("\n Answer is: %lf\n", ans);
}
|
code/computational_geometry/src/area_of_polygon/area_of_polygon.cpp | #include <iostream>
typedef std::pair<double, double> point;
const int size = 100000;
point points[size];
#define x first
#define y second
double calcArea(point a, point b, point c)
{
return abs( (a.first - b.first) * (c.second - b.second) - (a.second - b.second) *
(c.first - b.first) ) / 2;
}
int main ()
{
double answer = 0;
int n;
std::cin >> n;
for (int i = 0; i < n; i++)
std::cin >> points[i].x >> points[i].y;
for (int i = 2; i < n; i++)
answer += calcArea(points[0], points[i - 1], points[i]);
std::cout << answer;
}
|
code/computational_geometry/src/area_of_polygon/area_of_polygon.java | public class AreaOfPolygon {
public static void main(String []args){
// input points {xPoints[i],yPoints[j]}
int[] xPoints = {4, 4, 8, 8, -4, -4};
int[] yPoints = {6, -4, -4, -8, -8, 6};
double result = 0;
int j = xPoints.length - 1;
for (int i=0; i< xPoints.length; i++){
result += (xPoints[j] + xPoints[i]) * (yPoints[j] - yPoints[i]);
j = i;
}
result = result/2;
System.out.println(result);
}
}
|
code/computational_geometry/src/area_of_polygon/area_of_polygon.py | def area_of_polygon(verticeX, verticeY):
length = len(verticeX)
area = 0.0
for a in range(0, length):
b = (a + 1) % length
area += verticeX[a] * verticeY[b] - verticeX[b] * verticeY[a]
area = abs(area) / 2.0
return area
X = []
Y = []
try:
input = raw_input
except NameError:
pass
n = int(input("Enter number of vertices of the polygon:"))
for i in range(0, n):
X.append(float(input("X of vertex " + str(i + 1) + ": ")))
Y.append(float(input("Y of vertex " + str(i + 1) + ": ")))
print("Area of polygon : " + str(area_of_polygon(X, Y)))
|
code/computational_geometry/src/area_of_triangle/area_of_triangle.c | #include <stdio.h>
#include <stdlib.h>
float
area(float x1, float x2, float y1, float y2,
float z1, float z2)
{
return (fabsf((x1 - y1) * (z2 - y2) - (x2 - y2) * (z1 - y1)) / 2.0);
}
int
main()
{
float x1, x2, y1, y2, z1, z2;
printf("Enter x1 = ");
scanf("%f", &x1);
printf("Enter x2 = ");
scanf("%f", &x2);
printf("Enter y1 = ");
scanf("%f", &y1);
printf("Enter y2 = ");
scanf("%f", &y2);
printf("Enter z1 = ");
scanf("%f", &z1);
printf("Enter z2 = ");
scanf("%f", &z2);
printf("Area of the Triangle = %f \n", area(x1, x2, y1, y2, z1, z2));
return (0);
}
|
code/computational_geometry/src/area_of_triangle/area_of_triangle.cpp | #include <iostream>
typedef std::pair<double, double> point;
double calcArea(point a, point b, point c)
{
return abs( (a.first - b.first) * (c.second - b.second) - (a.second - b.second) *
(c.first - b.first) ) / 2;
}
int main ()
{
point a, b, c;
std::cin >> a.first >> a.second >> b.first >> b.second >> c.first >> c.second;
std::cout << calcArea(a, b, c);
}
|
code/computational_geometry/src/area_of_triangle/area_of_triangle.go | package main
// Part of Cosmos by OpenGenus Foundation
import (
"fmt"
"math"
)
type vector struct {
x, y float64
}
func calculateArea(a, b, c vector) float64 {
return math.Abs((a.x - b.x) * (c.y - b.y) - (a.y - b.y) * (c.x - b.x)) / 2
}
func main() {
a := vector{x: 5, y: 5}
b := vector{x: 5, y: 10}
c := vector{x: 10, y: 5}
// 12.5
fmt.Println(calculateArea(a, b, c))
a = vector{x: 2, y: 4}
b = vector{x: 3, y: 12}
c = vector{x: 8, y: 5}
// 23.5
fmt.Println(calculateArea(a, b, c))
}
|
code/computational_geometry/src/area_of_triangle/area_of_triangle.java | import java.lang.Math;
public class AreaOfTriangle {
public static void main(String []args){
// input points {x,y}
int[] pointA = {15,15};
int[] pointB = {23,30};
int[] pointC = {50,25};
double result = Math.abs(((pointA[0]*(pointB[1] - pointC[1])) + (pointB[0]*(pointC[1] - pointA[1])) + (pointC[0]*(pointA[1] - pointB[1])))/2);
System.out.println(result);
}
}
|
code/computational_geometry/src/area_of_triangle/area_of_triangle.js | // Part of Cosmos by OpenGenus Foundation
// Author: Igor Antun
// Github: @IgorAntun
// Function to find area of a triangle using three different vertices.
/* Function */
const area_of_triangle = (a, b, c) =>
Math.abs(
a.x * b.y + a.y * c.x + b.x * c.y - a.y * b.x - a.x * c.y - b.y * c.x
) / 2;
/* Test */
area_of_triangle({ x: 3, y: 50 }, { x: -6, y: 8 }, { x: 8, y: 0 }); // should return 330
|
code/computational_geometry/src/area_of_triangle/area_of_triangle.py | #! /usr/local/bin/python3
# Part of Cosmos by OpenGenus Foundation
# Programmer: Amariah Del Mar
# Date Written: October 6th, 2017
# Function to find area of a triangle using three different vertices.
class MyPoint:
def __init__(self, x=0, y=0):
self.x = x
self.y = y
def area_of_triangle(a, b, c):
area = 0.5 * abs(
(a.x * b.y)
+ (b.x * c.y)
+ (c.x * a.y)
- (a.x * c.y)
- (c.x * b.y)
- (b.x * a.y)
)
return area
def test(a, b, c):
a.x, a.y = 3, 50
b.x, b.y = -6, 8
c.x, c.y = 8, 0
return a, b, c
if __name__ == "__main__":
pt1 = MyPoint()
pt2 = MyPoint()
pt3 = MyPoint()
pt1, pt2, pt3 = test(pt1, pt2, pt3)
tri_area = area_of_triangle(pt1, pt2, pt3)
print(
"The area of a triangle with vertices ({},{}), ({},{}) and ({},{}) is {}.".format(
pt1.x, pt1.y, pt2.x, pt2.y, pt3.x, pt3.y, tri_area
)
)
|
code/computational_geometry/src/area_of_triangle/area_of_triangle.rs | struct Point {
x: f64,
y: f64
}
struct Triangle {
a: Point,
b: Point,
c: Point
}
impl Triangle {
fn area(&self) -> f64 {
// TODO: How can i destructure properly?
let ref a = self.a;
let ref b = self.b;
let ref c = self.c;
((a.x * b.y) + (a.y * c.x) + (b.x * c.y)
- (a.y * b.x) - (a.x * c.y) - (b.y * c.x)).abs() / 2.0
}
}
#[test]
fn test_tri_area() {
let tri = Triangle {
a: Point {
x: 3.0,
y: 50.0
},
b: Point {
x: -6.0,
y: 8.0
},
c: Point {
x: 8.0,
y: 0.0
}
};
assert_eq!(tri.area(), 330.0);
}
|
code/computational_geometry/src/area_of_triangle/area_of_triangle_herons_formula.cpp | #include <iostream>
#include <cmath>
class AreaOfTriangle
{
public:
AreaOfTriangle(double a, double b, double c) : a_(a), b_(b), c_(c) {}
double calculateArea();
private:
double a_, b_, c_;
};
double AreaOfTriangle::calculateArea()
{
/*
* As magnitude of length of sides must be positive.
* Given length of sides of triangle must follow the following result :
* "Sum of any two sides of triangle must be smaller than the third side of triangle".
*/
if (a_ < 0 || b_ < 0 || c_ < 0 || a_+ b_ <= c_ || a_+ c_ <= b_ || b_+ c_ <= a_)
return 0.0;
double s = (a_ + b_ + c_) / 2; //semi-perimeter of triangle
return sqrt(s * (s - a_) * (s - b_) * (s - c_)); //Heron's Formula
}
int main()
{
double ta, tb, tc;
std::cout << "\nEnter the length of side-1 : ";
std::cin >> ta;
std::cout << "\nEnter the length of side-2 : ";
std::cin >> tb;
std::cout << "\nEnter the length of side-3 : ";
std::cin >> tc;
AreaOfTriangle a(ta, tb, tc);
if (a.calculateArea() == 0.0)
std::cout << "\nInvalid Triangle";
else
std::cout << "\nArea of Triangle : " << a.calculateArea() << " square units.";
}
|
code/computational_geometry/src/axis_aligned_bounding_box_collision/axis_aligned_bounding_box_collision.cpp | #include <iostream>
// Part of Cosmos by OpenGenus Foundation
struct Vector
{
int x;
int y;
};
struct Shape
{
Vector center;
int width;
int height;
};
bool checkAABBCollision(Shape &a, Shape &b)
{
// change '<' to '<=' if you want to include edge touching as a collision
return (abs(a.center.x - b.center.x) * 2 < (a.width + b.width)) &&
(abs(a.center.y - b.center.y) * 2 < (a.height + b.height));
}
int main()
{
Shape a = { Vector {3, 3}, 4, 5 };
Shape b = { Vector {9, 3}, 6, 4 };
// 0 - no collision
std::cout << checkAABBCollision(a, b) << std::endl;
a = { Vector {3, 3}, 4, 5 };
b = { Vector {7, 3}, 6, 4 };
// 1 - collision
std::cout << checkAABBCollision(a, b) << std::endl;
a = { Vector {3, 10}, 4, 6 };
b = { Vector {3, 5}, 6, 6 };
// 1 - collision
std::cout << checkAABBCollision(a, b) << std::endl;
}
|
code/computational_geometry/src/axis_aligned_bounding_box_collision/axis_aligned_bounding_box_collision.go | package main
// Part of Cosmos by OpenGenus Foundation
import (
"fmt"
"math"
)
type vector struct {
x, y float64
}
type shape struct {
center vector
height, width float64
}
func checkAABBCollision(a, b shape) bool {
// change '<' to '<=' if you want to include edge touching as a collision
return (math.Abs(a.center.x - b.center.x) *2 < (a.width + b.width)) &&
(math.Abs(a.center.y - b.center.y) * 2 < (a.height + b.height))
}
func main() {
shapeA := shape{center: vector{3, 3}, height: 5, width: 4}
shapeB := shape{center: vector{9, 3}, height: 4, width: 6}
// 0 - no collision
fmt.Println(checkAABBCollision(shapeA, shapeB))
shapeA = shape{center: vector{3, 3}, height: 5, width: 4}
shapeB = shape{center: vector{7, 3}, height: 4, width: 6}
// 1 - collision
fmt.Println(checkAABBCollision(shapeA, shapeB))
shapeA = shape{center: vector{3, 10}, height: 6, width: 4}
shapeB = shape{center: vector{3, 5}, height: 6, width: 6}
// 1 - collision
fmt.Println(checkAABBCollision(shapeA, shapeB))
}
|
code/computational_geometry/src/bresenham_circle/bresenham_circle.cpp | #include <iostream>
#include "graphics.h"
class BresenhamCircle
{
public:
BresenhamCircle(int radius_) : radius_(radius_) { }
void getRadiusCenter();
void drawBresenhamCircle();
void displayBresenhmCircle(int xc_, int yc_, int x, int y);
private:
int radius_;
int xc_;
int yc_;
};
void BresenhamCircle::drawBresenhamCircle()
{
int x = 0, y = radius_;
int decesionParameter = 3 - 2 * radius_;
displayBresenhmCircle(xc_, yc_, x, y);
while (y >= x)
{
x++;
if (decesionParameter > 0)
{
y--;
decesionParameter = decesionParameter + 4 * (x - y) + 10;
}
else
decesionParameter = decesionParameter + 4 * x + 6;
displayBresenhmCircle(xc_, yc_, x, y); //displaying all the Eight Pixels of (x,y)
delay(30);
}
}
void BresenhamCircle::getRadiusCenter()
{
std::cout << "\nEnter Radius of the Circle : ";
std::cin >> radius_;
std::cout << "\nEnter X-Coordinate of Center of Circle : ";
std::cin >> xc_;
std::cout << "\nEnter Y-Coordinate of Center of Circle : ";
std::cin >> yc_;
}
void BresenhamCircle::displayBresenhmCircle(int xc_,int yc_, int x, int y)
{
//displaying all 8 coordinates of(x,y) residing in 8-octants
putpixel(xc_+x, yc_+y, WHITE);
putpixel(xc_-x, yc_+y, WHITE);
putpixel(xc_+x, yc_-y, WHITE);
putpixel(xc_-x, yc_-y, WHITE);
putpixel(xc_+y, yc_+x, WHITE);
putpixel(xc_-y, yc_+x, WHITE);
putpixel(xc_+y, yc_-x, WHITE);
putpixel(xc_-y, yc_-x, WHITE);
}
int main()
{
int gd = DETECT, gm;
initgraph(&gd, &gm, NULL);
BresenhamCircle b(0);
//accepting the radius and the centre coordinates of the circle
b.getRadiusCenter();
/*
* selecting the nearest pixel and displaying all the corresponding
* points of the nearest pixel point lying in 8-octants.
*
*/
b.drawBresenhamCircle();
delay(200);
closegraph();
}
|
code/computational_geometry/src/bresenham_circle/graphics.h | // The winbgim library, Version 6.0, August 9, 2004
// Written by:
// Grant Macklem ([email protected])
// Gregory Schmelter ([email protected])
// Alan Schmidt ([email protected])
// Ivan Stashak ([email protected])
// Michael Main ([email protected])
// CSCI 4830/7818: API Programming
// University of Colorado at Boulder, Spring 2003
// ---------------------------------------------------------------------------
// Notes
// ---------------------------------------------------------------------------
// * This library is still under development.
// * Please see http://www.cs.colorado.edu/~main/bgi for information on
// * using this library with the mingw32 g++ compiler.
// * This library only works with Windows API level 4.0 and higher (Windows 95, NT 4.0 and newer)
// * This library may not be compatible with 64-bit versions of Windows
// ---------------------------------------------------------------------------
// ---------------------------------------------------------------------------
// Macro Guard and Include Directives
// ---------------------------------------------------------------------------
#ifndef WINBGI_H
#define WINBGI_H
#include <windows.h> // Provides the mouse message types
#include <limits.h> // Provides INT_MAX
#include <sstream> // Provides std::ostringstream
// ---------------------------------------------------------------------------
// ---------------------------------------------------------------------------
// Definitions
// ---------------------------------------------------------------------------
// Definitions for the key pad extended keys are added here. When one
// of these keys are pressed, getch will return a zero followed by one
// of these values. This is the same way that it works in conio for
// dos applications.
#define KEY_HOME 71
#define KEY_UP 72
#define KEY_PGUP 73
#define KEY_LEFT 75
#define KEY_CENTER 76
#define KEY_RIGHT 77
#define KEY_END 79
#define KEY_DOWN 80
#define KEY_PGDN 81
#define KEY_INSERT 82
#define KEY_DELETE 83
#define KEY_F1 59
#define KEY_F2 60
#define KEY_F3 61
#define KEY_F4 62
#define KEY_F5 63
#define KEY_F6 64
#define KEY_F7 65
#define KEY_F8 66
#define KEY_F9 67
// Line thickness settings
#define NORM_WIDTH 1
#define THICK_WIDTH 3
// Character Size and Direction
#define USER_CHAR_SIZE 0
#define HORIZ_DIR 0
#define VERT_DIR 1
// Constants for closegraph
#define CURRENT_WINDOW -1
#define ALL_WINDOWS -2
#define NO_CURRENT_WINDOW -3
// The standard Borland 16 colors
#define MAXCOLORS 15
enum colors { BLACK, BLUE, GREEN, CYAN, RED, MAGENTA, BROWN, LIGHTGRAY, DARKGRAY,
LIGHTBLUE, LIGHTGREEN, LIGHTCYAN, LIGHTRED, LIGHTMAGENTA, YELLOW, WHITE };
// The standard line styles
enum line_styles { SOLID_LINE, DOTTED_LINE, CENTER_LINE, DASHED_LINE, USERBIT_LINE };
// The standard fill styles
enum fill_styles { EMPTY_FILL, SOLID_FILL, LINE_FILL, LTSLASH_FILL, SLASH_FILL,
BKSLASH_FILL, LTBKSLASH_FILL, HATCH_FILL, XHATCH_FILL, INTERLEAVE_FILL,
WIDE_DOT_FILL, CLOSE_DOT_FILL, USER_FILL };
// The various graphics drivers
enum graphics_drivers { DETECT, CGA, MCGA, EGA, EGA64, EGAMONO, IBM8514, HERCMONO,
ATT400, VGA, PC3270 };
// Various modes for each graphics driver
enum graphics_modes { CGAC0, CGAC1, CGAC2, CGAC3, CGAHI,
MCGAC0 = 0, MCGAC1, MCGAC2, MCGAC3, MCGAMED, MCGAHI,
EGALO = 0, EGAHI,
EGA64LO = 0, EGA64HI,
EGAMONOHI = 3,
HERCMONOHI = 0,
ATT400C0 = 0, ATT400C1, ATT400C2, ATT400C3, ATT400MED, ATT400HI,
VGALO = 0, VGAMED, VGAHI,
PC3270HI = 0,
IBM8514LO = 0, IBM8514HI };
// Borland error messages for the graphics window.
#define NO_CLICK -1 // No mouse event of the current type in getmouseclick
enum graph_errors { grInvalidVersion = -18, grInvalidDeviceNum = -15, grInvalidFontNum,
grInvalidFont, grIOerror, grError, grInvalidMode, grNoFontMem,
grFontNotFound, grNoFloodMem, grNoScanMem, grNoLoadMem,
grInvalidDriver, grFileNotFound, grNotDetected, grNoInitGraph,
grOk };
// Write modes
enum putimage_ops{ COPY_PUT, XOR_PUT, OR_PUT, AND_PUT, NOT_PUT };
// Text Modes
enum horiz { LEFT_TEXT, CENTER_TEXT, RIGHT_TEXT };
enum vertical { BOTTOM_TEXT, VCENTER_TEXT, TOP_TEXT }; // middle not needed other than as seperator
enum font_names { DEFAULT_FONT, TRIPLEX_FONT, SMALL_FONT, SANS_SERIF_FONT,
GOTHIC_FONT, SCRIPT_FONT, SIMPLEX_FONT, TRIPLEX_SCR_FONT,
COMPLEX_FONT, EUROPEAN_FONT, BOLD_FONT };
// ---------------------------------------------------------------------------
// ---------------------------------------------------------------------------
// Structures
// ---------------------------------------------------------------------------
// This structure records information about the last call to arc. It is used
// by getarccoords to get the location of the endpoints of the arc.
struct arccoordstype
{
int x, y; // Center point of the arc
int xstart, ystart; // The starting position of the arc
int xend, yend; // The ending position of the arc.
};
// This structure defines the fill style for the current window. Pattern is
// one of the system patterns such as SOLID_FILL. Color is the color to
// fill with
struct fillsettingstype
{
int pattern; // Current fill pattern
int color; // Current fill color
};
// This structure records information about the current line style.
// linestyle is one of the line styles such as SOLID_LINE, upattern is a
// 16-bit pattern for user defined lines, and thickness is the width of the
// line in pixels.
struct linesettingstype
{
int linestyle; // Current line style
unsigned upattern; // 16-bit user line pattern
int thickness; // Width of the line in pixels
};
// This structure records information about the text settings.
struct textsettingstype
{
int font; // The font in use
int direction; // Text direction
int charsize; // Character size
int horiz; // Horizontal text justification
int vert; // Vertical text justification
};
// This structure records information about the viewport
struct viewporttype
{
int left, top, // Viewport bounding box
right, bottom;
int clip; // Whether to clip image to viewport
};
// This structure records information about the palette.
struct palettetype
{
unsigned char size;
signed char colors[MAXCOLORS + 1];
};
// ---------------------------------------------------------------------------
// ---------------------------------------------------------------------------
// API Entries
// ---------------------------------------------------------------------------
#ifdef __cplusplus
extern "C" {
#endif
// Drawing Functions
void arc( int x, int y, int stangle, int endangle, int radius );
void bar( int left, int top, int right, int bottom );
void bar3d( int left, int top, int right, int bottom, int depth, int topflag );
void circle( int x, int y, int radius );
void cleardevice( );
void clearviewport( );
void drawpoly(int n_points, int* points);
void ellipse( int x, int y, int stangle, int endangle, int xradius, int yradius );
void fillellipse( int x, int y, int xradius, int yradius );
void fillpoly(int n_points, int* points);
void floodfill( int x, int y, int border );
void line( int x1, int y1, int x2, int y2 );
void linerel( int dx, int dy );
void lineto( int x, int y );
void pieslice( int x, int y, int stangle, int endangle, int radius );
void putpixel( int x, int y, int color );
void rectangle( int left, int top, int right, int bottom );
void sector( int x, int y, int stangle, int endangle, int xradius, int yradius );
// Miscellaneous Functions
int getdisplaycolor( int color );
int converttorgb( int color );
void delay( int msec );
void getarccoords( arccoordstype *arccoords );
int getbkcolor( );
int getcolor( );
void getfillpattern( char *pattern );
void getfillsettings( fillsettingstype *fillinfo );
void getlinesettings( linesettingstype *lineinfo );
int getmaxcolor( );
int getmaxheight( );
int getmaxwidth( );
int getmaxx( );
int getmaxy( );
bool getrefreshingbgi( );
int getwindowheight( );
int getwindowwidth( );
int getpixel( int x, int y );
void getviewsettings( viewporttype *viewport );
int getx( );
int gety( );
void moverel( int dx, int dy );
void moveto( int x, int y );
void refreshbgi(int left, int top, int right, int bottom);
void refreshallbgi( );
void setbkcolor( int color );
void setcolor( int color );
void setfillpattern( char *upattern, int color );
void setfillstyle( int pattern, int color );
void setlinestyle( int linestyle, unsigned upattern, int thickness );
void setrefreshingbgi(bool value);
void setviewport( int left, int top, int right, int bottom, int clip );
void setwritemode( int mode );
// Window Creation / Graphics Manipulation
void closegraph( int wid=ALL_WINDOWS );
void detectgraph( int *graphdriver, int *graphmode );
void getaspectratio( int *xasp, int *yasp );
char *getdrivername( );
int getgraphmode( );
int getmaxmode( );
char *getmodename( int mode_number );
void getmoderange( int graphdriver, int *lomode, int *himode );
void graphdefaults( );
char *grapherrormsg( int errorcode );
int graphresult( );
void initgraph( int *graphdriver, int *graphmode, char *pathtodriver );
int initwindow
( int width, int height, const char* title="Windows BGI", int left=0, int top=0, bool dbflag=false, bool closeflag=true );
int installuserdriver( char *name, int *fp ); // Not available in WinBGI
int installuserfont( char *name ); // Not available in WinBGI
int registerbgidriver( void *driver ); // Not available in WinBGI
int registerbgifont( void *font ); // Not available in WinBGI
void restorecrtmode( );
void setaspectratio( int xasp, int yasp );
unsigned setgraphbufsize( unsigned bufsize ); // Not available in WinBGI
void setgraphmode( int mode );
void showerrorbox( const char *msg = NULL );
// User Interaction
int getch( );
int kbhit( );
// User-Controlled Window Functions (winbgi.cpp)
int getcurrentwindow( );
void setcurrentwindow( int window );
// Double buffering support (winbgi.cpp)
int getactivepage( );
int getvisualpage( );
void setactivepage( int page );
void setvisualpage( int page );
void swapbuffers( );
// Image Functions (drawing.cpp)
unsigned imagesize( int left, int top, int right, int bottom );
void getimage( int left, int top, int right, int bottom, void *bitmap );
void putimage( int left, int top, void *bitmap, int op );
void printimage(
const char* title=NULL,
double width_inches=7, double border_left_inches=0.75, double border_top_inches=0.75,
int left=0, int top=0, int right=INT_MAX, int bottom=INT_MAX,
bool active=true, HWND hwnd=NULL
);
void readimagefile(
const char* filename=NULL,
int left=0, int top=0, int right=INT_MAX, int bottom=INT_MAX
);
void writeimagefile(
const char* filename=NULL,
int left=0, int top=0, int right=INT_MAX, int bottom=INT_MAX,
bool active=true, HWND hwnd=NULL
);
// Text Functions (text.cpp)
void gettextsettings(struct textsettingstype *texttypeinfo);
void outtext(char *textstring);
void outtextxy(int x, int y, char *textstring);
void settextjustify(int horiz, int vert);
void settextstyle(int font, int direction, int charsize);
void setusercharsize(int multx, int divx, int multy, int divy);
int textheight(char *textstring);
int textwidth(char *textstring);
extern std::ostringstream bgiout;
void outstream(std::ostringstream& out=bgiout);
void outstreamxy(int x, int y, std::ostringstream& out=bgiout);
// Mouse Functions (mouse.cpp)
void clearmouseclick( int kind );
void clearresizeevent( );
void getmouseclick( int kind, int& x, int& y );
bool ismouseclick( int kind );
bool isresizeevent( );
int mousex( );
int mousey( );
void registermousehandler( int kind, void h( int, int ) );
void setmousequeuestatus( int kind, bool status=true );
// Palette Functions
palettetype *getdefaultpalette( );
void getpalette( palettetype *palette );
int getpalettesize( );
void setallpalette( palettetype *palette );
void setpalette( int colornum, int color );
void setrgbpalette( int colornum, int red, int green, int blue );
// Color Macros
#define IS_BGI_COLOR(v) ( ((v) >= 0) && ((v) < 16) )
#define IS_RGB_COLOR(v) ( (v) & 0x03000000 )
#define RED_VALUE(v) int(GetRValue( converttorgb(v) ))
#define GREEN_VALUE(v) int(GetGValue( converttorgb(v) ))
#define BLUE_VALUE(v) int(GetBValue( converttorgb(v) ))
#undef COLOR
int COLOR(int r, int g, int b); // No longer a macro
#ifdef __cplusplus
}
#endif
// ---------------------------------------------------------------------------
#endif // WINBGI_H
|
code/computational_geometry/src/bresenham_line/bresenham_line.cpp | // Part of Cosmos by OpenGenus Foundation
#include <functional>
template<typename Color, typename fabs>
void Line(float x1, float y1, float x2, float y2, const Color& color )
{
const bool steep = (fabs(y2 - y1) > fabs(x2 - x1));
if (steep)
{
std::swap(x1, y1);
std::swap(x2, y2);
}
if (x1 > x2)
{
std::swap(x1, x2);
std::swap(y1, y2);
}
const float dx = x2 - x1;
const float dy = fabs(y2 - y1);
float error = dx / 2.0f;
const int ystep = (y1 < y2) ? 1 : -1;
int y = (int)y1;
const int maxX = (int)x2;
for (int x = (int)x1; x < maxX; x++)
{
if (steep)
SetPixel(y, x, color);
else
SetPixel(x, y, color);
error -= dy;
if (error < 0)
{
y += ystep;
error += dx;
}
}
}
|
code/computational_geometry/src/bresenham_line/bresenham_line.java | package applet;
import java.awt.Color;
import java.awt.Dimension;
import java.awt.Graphics;
import java.awt.event.MouseEvent;
import java.awt.event.MouseListener;
import java.awt.event.MouseMotionListener;
public class bresenhamLine extends java.applet.Applet implements MouseListener, MouseMotionListener {
private static final long serialVersionUID = 1L;
int width, height;
int xa = 0;
int ya = 0;
int xb = 0;
int yb = 0;
int pixelsize = 2;
/**
* This method does initialization
* @param no parameters used .
*/
public void init() {
this.width = getSize().width;
this.height = getSize().height;
this.addMouseListener(this);
this.addMouseMotionListener(this);
}
/**
* This method is used to Draw Line.
* @param xa first coordinate
* @param ya first Coordinate
* @param xb Second Coordinate
* @param yb Second Coordinate
* @return will not return anything .
*/
public void bresenhamLineDraw(int xa, int ya, int xb, int yb) {
// if point xa, ya is on the right side of point xb, yb, change them
if ((xa - xb) > 0) {
bresenhamLineDraw(xb, yb, xa, ya);
return;
}
// test inclination of line
// function Math.abs(y) defines absolute value y
if (Math.abs(yb - ya) > Math.abs(xb - xa)) {
// line and y axis angle is less then 45 degrees
// thats why go on the next procedure
bresteepLine(ya, xa, yb, xb);
return;
}
// line and x axis angle is less then 45 degrees, so x is guiding
// auxiliary variables
int x = xa, y = ya, sum = xb - xa, Dx = 2 * (xb - xa), Dy = Math.abs(2 * (yb - ya));
int delta_Dy = ((yb - ya) > 0) ? 1 : -1;
// draw line
for (int i = 0; i <= xb - xa; i++) {
setpix(x, y);
x++;
sum -= Dy;
if (sum < 0) {
y += delta_Dy;
sum += Dx;
}
}
}
/**
* This method is used to Draw Steeper Line.
* @param xc first coordinate
* @param yc first Coordinate
* @param xd Second Coordinate
* @param yd Second Coordinate
* @return will not return anything .
*/
public void bresteepLine(int xc, int yc, int xd, int yd) {
/** if point xc, yc is on the right side
of point xd yd,
change them
**/
if ((xc - xd) > 0) {
bresteepLine(xd, yd, xc, yc);
return;
}
int x = xc, y = yc, sum = xd - xc, Dx = 2 * (xd - xc), Dy = Math.abs(2 * (yd - yc));
int delta_Dy = ((yd - yc) > 0) ? 1 : -1;
for (int i = 0; i <= xd - xc; i++) {
setPix(y, x);
x++;
sum -= Dy;
if (sum < 0) {
y += delta_Dy;
sum += Dx;
}
}
}
/**
* This method is used to Set pixel for Line.
* @param x first coordinate
* @param y first Coordinate
* @return will not return anything .
*/
public void setPix(int x, int y) {
Graphics g = getGraphics();
g.setColor(Color.green);
g.fillRect(pixelsize * x, pixelsize * y, pixelsize, pixelsize);
}
/**
* This method is used to paint the line on screen.
* @param g of graphics library
* @return will not return anything .
*/
public void paint(Graphics g) {
Dimension d = getSize();
g.drawLine(0, 0, d.width, 0);
g.drawLine(0, 0, 0, d.height);
g.drawLine(d.width - 1, d.height - 1, d.width - 1, 0);
g.drawLine(d.width - 1, d.height - 1, 0, d.height - 1);
bresenhamLineDraw(xa, ya, xb, yb);
}
public void mousePressed(MouseEvent e) {
xa = e.getX() / pixelsize;
ya = e.getY() / pixelsize;
}
public void mouseDragged(MouseEvent e) {
xb = e.getX() / pixelsize;
yb = e.getY() / pixelsize;
repaint();
}
public void mouseReleased(MouseEvent e) {
}
public void mouseClicked(MouseEvent e) {
}
public void mouseEntered(MouseEvent e) {
}
public void mouseExited(MouseEvent e) {
}
public void mouseMoved(MouseEvent e) {
}
}
/**
* Sample Input - Enter Start X: 100
* Enter Start Y: 100
* Enter End X: 300
* Enter End Y: 300
* Sample output - https://ibb.co/NxYdXqd
*
*/
|
code/computational_geometry/src/bresenham_line/bresenham_line.py | def calc_del(x1, x2, y1, y2):
"""
Calculate the delta values for x and y co-ordinates
"""
return x2 - x1, y2 - y1
def bresenham(x1, y1, x2, y2):
"""
Calculate the co-ordinates for Bresehnam lines
bresenham(x1, y1, x2, y2)
returns a list of tuple of points
"""
swap = False
# Calculate delta for x and y
delX, delY = calc_del(x1, x2, y1, y2)
# Swap x and y if y > x
if abs(delY) > abs(delX):
x1, y1 = y1, x1
x2, y2 = y2, x2
# Swap x and y co-ordinates if x1 > x2
if x1 > x2:
swap = True
x1, x2 = x2, x1
y1, y2 = y2, y1
# Recalculate delta for x and y
delX, delY = calc_del(x1, x2, y1, y2)
# calculate step and error
step = 1 if y1 < y2 else -1
error = int(delX / 2.0)
y = y1
co_ords = []
# Calculate co-ordinates for the bresenham line
for x in range(x1, x2 + 1):
point = (x, y) if abs(delX) > abs(delY) else (y, x)
error -= abs(delY)
if error < 0:
y += step
error += delX
co_ords.append(point)
return co_ords if abs(delX) > abs(delY) else co_ords[::-1]
def main():
x1, y1, x2, y2 = int(input())
print(bresenham(x1, y1, x2, y2))
|
code/computational_geometry/src/bresenham_line/bresenham_line2.py | # Import graphics library
from graphics import GraphWin
import time
def bresenham_line(xa, ya, xb, yb):
dx = abs(xb - xa)
dy = abs(yb - ya)
slope = dy / float(dx)
x, y = xa, ya
# creating the window
win = GraphWin('Bresenham Line', 600, 480)
# checking the slope if slope > 1
# then interchange the role of x and y
if slope > 1:
dx, dy = dy, dx
x, y = y, x
xa, ya = ya, xa
xb, yb = yb, xb
# initialization of the inital disision parameter
p = 2 * dy - dx
Put_Pixel(win, x, y) # Plot Pixels To Draw Line
for k in range(2, dx):
if p > 0:
y += 1 if y < yb else y - 1
p += 2 * (dy - dx)
else:
p += 2 * dy
x += 1 if x < xb else x - 1
time.sleep(0.01) # delay for 0.01 secs
Put_Pixel(win, x, y) # Plot Pixels To Draw Line
def Put_Pixel(win, x, y):
"""Plot a pixel In the window at point (x, y)"""
pt = Point(x, y)
pt.draw(win)
def main():
# Taking coordinates from User
xa = int(input("Enter Start X: "))
ya = int(input("Enter Start Y: "))
xb = int(input("Enter End X: "))
yb = int(input("Enter End Y: "))
# Calling Out The function
Bresenham_Line(xa, ya, xb, yb)
# Driver Function
if __name__ == "__main__":
main()
# Input - Enter Start X : 100
# Enter Start Y : 100
# Enter End X : 300
# Enter End Y : 300
# Sample output - https://ibb.co/4fzGM6W |
code/computational_geometry/src/chans_algorithm/chans_algorithm.cpp | #include <iostream>
#include <stdlib.h>
#include <vector>
#include <algorithm> // For qsort() algorithm
#include <utility> // For pair() STL
#define RIGHT_TURN -1 // CW
#define LEFT_TURN 1 // CCW
#define COLLINEAR 0 // Collinear
using namespace std;
/*
* Class to handle the 2D Points!
*/
class Point
{
public:
int x;
int y;
Point (int newx = 0, int newy = 0)
{
x = newx;
y = newy;
}
/*
* Overloaded == operator to check for equality between 2 objects of class Point
*/
friend bool operator== (const Point& p1, const Point& p2)
{
return p1.x == p2.x && p1.y == p2.y;
}
/*
* Overloaded != operator to check for non-equality between 2 objects of class Point
*/
friend bool operator!= (const Point& p1, const Point& p2)
{
return !(p1.x == p2.x && p1.y == p2.y);
}
/*
* Overloaded ostream << operator to check for print object of class Point to STDOUT
*/
friend ostream& operator<<(ostream& output, const Point& p)
{
output << "(" << p.x << "," << p.y << ")";
return output;
}
} p0; // Global Point class object
/*
* Returns square of the distance between the two Point class objects
* @param p1: Object of class Point aka first Point
* @param p2: Object of class Point aka second Point
*/
int dist(Point p1, Point p2)
{
return (p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y);
}
/*
* Returns orientation of the line joining Points p and q and line joining Points q and r
* Returns -1 : CW orientation
+1 : CCW orientation
* 0 : Collinear
* @param p: Object of class Point aka first Point
* @param q: Object of class Point aka second Point
* @param r: Object of class Point aka third Point
*/
int orientation(Point p, Point q, Point r)
{
int val = (q.y - p.y) * (r.x - q.x) - (q.x - p.x) * (r.y - q.y);
if (val == 0)
return 0; // Collinear
return (val > 0) ? -1 : 1; // CW: -1 or CCW: 1
}
/*
* Predicate function used while sorting the Points using qsort() inbuilt function in C++
* @param p: Object of class Point aka first Point
* @param p: Object of class Point aka second Point
*/
int compare(const void *vp1, const void *vp2)
{
Point *p1 = (Point *)vp1;
Point *p2 = (Point *)vp2;
int orient = orientation(p0, *p1, *p2);
if (orient == 0)
return (dist(p0, *p2) >= dist(p0, *p1)) ? -1 : 1;
return (orient == 1) ? -1 : 1;
}
/*
* Returns the index of the Point to which the tangent is drawn from Point p.
* Uses a modified Binary Search Algorithm to yield tangent in O(log n) complexity
* @param v: vector of objects of class Points representing the hull aka the vector of hull Points
* @param p: Object of class Point from where tangent needs to be drawn
*/
int tangent(vector<Point> v, Point p)
{
int l = 0;
int r = v.size();
int l_before = orientation(p, v[0], v[v.size() - 1]);
int l_after = orientation(p, v[0], v[(l + 1) % v.size()]);
while (l < r)
{
int c = ((l + r) >> 1);
int c_before = orientation(p, v[c], v[(c - 1) % v.size()]);
int c_after = orientation(p, v[c], v[(c + 1) % v.size()]);
int c_side = orientation(p, v[l], v[c]);
if (c_before != RIGHT_TURN and c_after != RIGHT_TURN)
return c;
else if ((c_side == LEFT_TURN) and (l_after == RIGHT_TURN or l_before ==
l_after) or (c_side == RIGHT_TURN and c_before ==
RIGHT_TURN))
r = c;
else
l = c + 1;
l_before = -c_after;
l_after = orientation(p, v[l], v[(l + 1) % v.size()]);
}
return l;
}
/*
* Returns the pair of integers representing the Hull # and the Point in that Hull which is the extreme amongst all given Hull Points
* @param hulls: Vector containing the hull Points for various hulls stored as individual vectors.
*/
pair<int, int> extreme_hullpt_pair(vector<vector<Point>>& hulls)
{
int h = 0, p = 0;
for (int i = 0; i < hulls.size(); ++i)
{
int min_index = 0, min_y = hulls[i][0].y;
for (int j = 1; j < hulls[i].size(); ++j)
if (hulls[i][j].y < min_y)
{
min_y = hulls[i][j].y;
min_index = j;
}
if (hulls[i][min_index].y < hulls[h][p].y)
{
h = i;
p = min_index;
}
}
return make_pair(h, p);
}
/*
* Returns the pair of integers representing the Hull # and the Point in that Hull to which the Point lPoint will be joined
* @param hulls: Vector containing the hull Points for various hulls stored as individual vectors.
* @param lPoint: Pair of the Hull # and the leftmost extreme Point contained in that hull, amongst all the obtained hulls
*/
pair<int, int> next_hullpt_pair(vector<vector<Point>>& hulls, pair<int, int> lPoint)
{
Point p = hulls[lPoint.first][lPoint.second];
pair<int, int> next = make_pair(lPoint.first, (lPoint.second + 1) % hulls[lPoint.first].size());
for (int h = 0; h < hulls.size(); h++)
if (h != lPoint.first)
{
int s = tangent(hulls[h], p);
Point q = hulls[next.first][next.second];
Point r = hulls[h][s];
int t = orientation(p, q, r);
if (t == RIGHT_TURN || (t == COLLINEAR) && dist(p, r) > dist(p, q))
next = make_pair(h, s);
}
return next;
}
/*
* Constraint to find the outermost boundary of the Points by checking if the Points lie to the left otherwise adding the given Point p
* Returns the Hull Points
* @param v: Vector of all the Points
* @param p: New Point p which will be checked to be in the Hull Points or not
*/
vector<Point> keep_left (vector<Point>& v, Point p)
{
while (v.size() > 1 && orientation(v[v.size() - 2], v[v.size() - 1], p) != LEFT_TURN)
v.pop_back();
if (!v.size() || v[v.size() - 1] != p)
v.push_back(p);
return v;
}
/*
* Graham Scan algorithm to find convex hull from the given set of Points
* @param Points: List of the given Points in the cluster (as obtained by Chan's Algorithm grouping)
* Returns the Hull Points in a vector
*/
vector<Point> GrahamScan(vector<Point>& Points)
{
if (Points.size() <= 1)
return Points;
qsort(&Points[0], Points.size(), sizeof(Point), compare);
vector<Point> lower_hull;
for (int i = 0; i < Points.size(); ++i)
lower_hull = keep_left(lower_hull, Points[i]);
reverse(Points.begin(), Points.end());
vector<Point> upper_hull;
for (int i = 0; i < Points.size(); ++i)
upper_hull = keep_left(upper_hull, Points[i]);
for (int i = 1; i < upper_hull.size(); ++i)
lower_hull.push_back(upper_hull[i]);
return lower_hull;
}
/*
* Implementation of Chan's Algorithm to compute Convex Hull in O(nlogh) complexity
*/
vector<Point> chansalgorithm(vector<Point> v)
{
for (int t = 0; t < v.size(); ++t)
for (int m = 1; m < (1 << (1 << t)); ++m)
{
vector<vector<Point>> hulls;
for (int i = 0; i < v.size(); i = i + m)
{
vector<Point> chunk;
if (v.begin() + i + m <= v.end())
chunk.assign(v.begin() + i, v.begin() + i + m);
else
chunk.assign(v.begin() + i, v.end());
hulls.push_back(GrahamScan(chunk));
}
cout << "\nM (Chunk Size): " << m << "\n";
for (int i = 0; i < hulls.size(); ++i)
{
cout << "Convex Hull for Hull #" << i << " (Obtained using Graham Scan!!)\n";
for (int j = 0; j < hulls[i].size(); ++j)
cout << hulls[i][j] << " ";
cout << "\n";
}
vector<pair<int, int>> hull;
hull.push_back(extreme_hullpt_pair(hulls));
for (int i = 0; i < m; ++i)
{
pair<int, int> p = next_hullpt_pair(hulls, hull[hull.size() - 1]);
vector<Point> output;
if (p == hull[0])
{
for (int j = 0; j < hull.size(); ++j)
output.push_back(hulls[hull[j].first][hull[j].second]);
return output;
}
hull.push_back(p);
}
}
}
int main()
{
int T = 0, x = 0, y = 0;
cout << "Enter Total Number of points";
cin >> T;
if (T <= 0)
return -1;
Point Points[T];
for (int i = 0; i < T; ++i)
{
cin >> x >> y;
Points[i].x = x;
Points[i].y = y;
}
vector<Point> v(Points, Points + T);
vector<Point> output = chansalgorithm(v);
cout << " \ n-------------------- After Using Chan
's Algorithm --------------------\n";
cout << "\n******************** CONVEX HULL ********************\n";
for (int i = 0; i < output.size(); ++i)
cout << output[i] << " ";
cout << "\n";
return 0;
}
|
code/computational_geometry/src/cohen_sutherland_lineclip/README.md | # Working of Cohem Sutherland Line-clipping
## Enter the co-ordinates
Enter x1 and y1
## `100` `100`
Enter x2 and y2
## `200` `200`
## Before Clipping -
## After Clipping -

---
<p align="center">
A massive collaborative effort by <a href="https://github.com/OpenGenus/cosmos">OpenGenus Foundation</a>
</p>
---
|
code/computational_geometry/src/cohen_sutherland_lineclip/cohen_sutherland_lineclip.c | #include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<graphics.h>
#include<dos.h>
typedef struct coordinate
{
int x,y;
char code[4];
}PT;
void drawwindow();
void drawline(PT p1,PT p2);
PT setcode(PT p);
int visibility(PT p1,PT p2);
PT resetendpt(PT p1,PT p2);
int main()
{
int gd=DETECT,v,gm;
PT p1,p2,p3,p4,ptemp;
printf("\nEnter x1 and y1\n");
scanf("%d %d",&p1.x,&p1.y);
printf("\nEnter x2 and y2\n");
scanf("%d %d",&p2.x,&p2.y);
initgraph(&gd,&gm,"c:\\turboc3\\bgi");
drawwindow();
delay(500);
drawline(p1,p2);
delay(500);
cleardevice();
delay(500);
p1=setcode(p1);
p2=setcode(p2);
v=visibility(p1,p2);
delay(500);
switch(v)
{
case 0: drawwindow();
delay(500);
drawline(p1,p2);
break;
case 1: drawwindow();
delay(500);
break;
case 2: p3=resetendpt(p1,p2);
p4=resetendpt(p2,p1);
drawwindow();
delay(500);
drawline(p3,p4);
break;
}
delay(5000);
closegraph();
}
void drawwindow()
{
line(150,100,450,100);
line(450,100,450,350);
line(450,350,150,350);
line(150,350,150,100);
}
void drawline(PT p1,PT p2)
{
line(p1.x,p1.y,p2.x,p2.y);
}
PT setcode(PT p) //for setting the 4 bit code
{
PT ptemp;
if(p.y<100)
ptemp.code[0]='1'; //Top
else
ptemp.code[0]='0';
if(p.y>350)
ptemp.code[1]='1'; //Bottom
else
ptemp.code[1]='0';
if(p.x>450)
ptemp.code[2]='1'; //Right
else
ptemp.code[2]='0';
if(p.x<150)
ptemp.code[3]='1'; //Left
else
ptemp.code[3]='0';
ptemp.x=p.x;
ptemp.y=p.y;
return(ptemp);
}
int visibility(PT p1,PT p2)
{
int i,flag=0;
for(i=0;i<4;i++)
{
if((p1.code[i]!='0') || (p2.code[i]!='0'))
flag=1;
}
if(flag==0)
return(0);
for(i=0;i<4;i++)
{
if((p1.code[i]==p2.code[i]) && (p1.code[i]=='1'))
flag='0';
}
if(flag==0)
return(1);
return(2);
}
PT resetendpt(PT p1,PT p2)
{
PT temp;
int x,y,i;
float m,k;
if(p1.code[3]=='1')
x=150;
if(p1.code[2]=='1')
x=450;
if((p1.code[3]=='1') || (p1.code[2]=='1'))
{
m=(float)(p2.y-p1.y)/(p2.x-p1.x);
k=(p1.y+(m*(x-p1.x)));
temp.y=k;
temp.x=x;
for(i=0;i<4;i++)
temp.code[i]=p1.code[i];
if(temp.y<=350 && temp.y>=100)
return (temp);
}
if(p1.code[0]=='1')
y=100;
if(p1.code[1]=='1')
y=350;
if((p1.code[0]=='1') || (p1.code[1]=='1'))
{
m=(float)(p2.y-p1.y)/(p2.x-p1.x);
k=(float)p1.x+(float)(y-p1.y)/m;
temp.x=k;
temp.y=y;
for(i=0;i<4;i++)
temp.code[i]=p1.code[i];
return(temp);
}
else
return(p1);
}
|
code/computational_geometry/src/cohen_sutherland_lineclip/cohen_sutherland_lineclip.cpp | #include <iostream>
class CohenSutherLandAlgo
{
public:
CohenSutherLandAlgo() : x1_(0.0), x2_(0.0), y1_(0.0), y2_(0.0) { }
void setCoordinates(double x1, double y1, double x2, double y2);
void setClippingRectangle(double x_max, double y_max, double x_min, double y_min);
int generateCode(double x, double y);
void cohenSutherland();
private:
double x1_, y1_, x2_, y2_;
double xMax_, yMax_, xMin_, yMin_;
const int Inside = 0; // 0000
const int Left = 1; // 0001
const int Right = 2; // 0010
const int Bottom = 4; // 0100
const int Top = 8; // 1000
};
void CohenSutherLandAlgo::setCoordinates(double x1, double y1, double x2, double y2)
{
this->x1_ = x1;
this->y1_ = y1;
this->x2_ = x2;
this->y2_ = y2;
}
void CohenSutherLandAlgo::setClippingRectangle(double x_max, double y_max, double x_min, double y_min)
{
this->xMax_ = x_max;
this->yMax_ = y_max;
this->xMin_ = x_min;
this->yMin_ = y_min;
}
int CohenSutherLandAlgo::generateCode(double x, double y)
{
int code = Inside; // intially initializing as being inside
if (x < xMin_) // lies to the left of rectangle
code |= Left;
else if (x > xMax_) // lies to the right of rectangle
code |= Right;
if (y < yMin_) // lies below the rectangle
code |= Bottom;
else if (y > yMax_) // lies above the rectangle
code |= Top;
return code;
}
void CohenSutherLandAlgo::cohenSutherland()
{
int code1 = generateCode(x1_, y1_); // Compute region codes for P1.
int code2 = generateCode(x2_, y2_); // Compute region codes for P2.
bool accept = false; // Initialize line as outside the rectangular window.
while (true)
{
if ((code1 == 0) && (code2 == 0))
{
// If both endpoints lie within rectangle.
accept = true;
break;
}
else if (code1 & code2)
{
break; // If both endpoints are outside rectangle,in same region.
}
else
{
// Some segment of line lies within the rectangle.
int codeOut;
double x, y;
// At least one endpoint lies outside the rectangle, pick it.
if (code1 != 0)
codeOut = code1;
else
codeOut = code2;
/*
* Find intersection point by using formulae :
y = y1 + slope * (x - x1)
x = x1 + (1 / slope) * (y - y1)
*/
if (codeOut & Top)
{
// point is above the clip rectangle
x = x1_ + (x2_ - x1_) * (yMax_ - y1_) / (y2_ - y1_);
y = yMax_;
}
else if (codeOut & Bottom)
{
// point is below the rectangle
x = x1_ + (x2_ - x1_) * (yMin_ - y1_) / (y2_ - y1_);
y = yMin_;
}
else if (codeOut & Right)
{
// point is to the right of rectangle
y = y1_ + (y2_ - y1_) * (xMax_ - x1_) / (x2_ - x1_);
x = xMax_;
}
else if (codeOut & Left)
{
// point is to the left of rectangle
y = y1_ + (y2_ - y1_) * (xMin_ - x1_) / (x2_ - x1_);
x = xMin_;
}
/*
* Intersection point x,y is found.
Replace point outside rectangle by intersection point.
*/
if (codeOut == code1)
{
x1_ = x;
y1_ = y;
code1 = generateCode(x1_, y1_);
}
else
{
x2_ = x;
y2_ = y;
code2 = generateCode(x2_, y2_);
}
}
}
if (accept)
{
std::cout <<"Line accepted from " <<"("<< x1_ << ", "
<< y1_ << ")" << " to "<< "(" << x2_ << ", " << y2_ << ")" << std::endl;
}
else
std::cout << "Line rejected" << std::endl;
}
int main() {
CohenSutherLandAlgo c;
double x1, y1, x2, y2, x_max, y_max, x_min, y_min;
std::cout << "\nEnter Co-ordinates of P1(X1,Y1) of Line Segment : ";
std::cout << "\nEnter X1 Co-ordinate : ";
std::cin >> x1;
std::cout << "\nEnter Y1 Co-ordinate : ";
std::cin >> y1;
std::cout << "\nEnter Co-ordinates of P2(X2,Y2) of Line Segment : ";
std::cout << "\nEnter X2 Co-ordinate : ";
std::cin >> x2;
std::cout << "\nEnter Y2 Co-ordinate : ";
std::cin >> y2;
c.setCoordinates(x1, y1, x2, y2);
std::cout << "\nEnter the Co-ordinates of Interested Rectangle.";
std::cout << "\nEnter the X_MAX : ";
std::cin >> x_max;
std::cout << "\nEnter the Y_MAX : ";
std::cin >> y_max;
std::cout << "\nEnter the X_MIN : ";
std::cin >> x_min;
std::cout << "\nEnter the Y_MIN : ";
std::cin >> y_min;
c.setClippingRectangle(x_max, y_max, x_min, y_min);
c.cohenSutherland();
}
|
code/computational_geometry/src/dda_line/dda_line.cpp | #include <iostream>
class DDALineDrawingAlgorithm
{
public:
void ddaLineDrawing();
void getCoordinates();
private:
int x1_, x2_, y1_, y2_;
};
void DDALineDrawingAlgorithm::ddaLineDrawing()
{
//calculating range for line between start and end point
int dx = x2_ - x1_;
int dy = y2_ - y1_;
// calculate steps required for creating pixels
int step = abs(abs(dx) > abs(dy) ? dx : dy);
// calculate increment in x & y for each steps
float xIncrement = (dx) / (float)step;
float yIncrement = (dy) / (float)step;
// drawing pixel for each step
float x = x1_;
float y = y1_;
putpixel((x), (y),GREEN); //this putpixel is for very first pixel of the line
for(int i = 1; i <= step; ++i)
{
x = x + xIncrement; // increment in x at each step
y = y + yIncrement; // increment in y at each step
putpixel(round(x), round(y),GREEN); // display pixel at coordinate (x, y)
delay(200); //delay introduced for visualization at each step
}
delay(500);
}
void DDALineDrawingAlgorithm::getCoordinates()
{
std::cout << "\nEnter the First Coordinate ";
std::cout << "\nEnter X1 : ";
std::cin >> x1_;
std::cout << "\nEnter Y1 : ";
std::cin >> y1_;
std::cout << "\nEnter the Second Coordinate ";
std::cout << "\nEnter X2 : ";
std::cin >> x2_;
std::cout << "\nEnter Y2 : ";
std::cin >> y2_;
}
int main()
{
DDALineDrawingAlgorithm d;
d.getCoordinates();
int gd=DETECT,gm;
initgraph(&gd,&gm,NULL);
d.ddaLineDrawing();
}
|
code/computational_geometry/src/distance_between_points/README.md | # Distance Between two Points
Calculating the distance between two points is done by creating a right-angled triangle using the two points. The line between the two points is the hypotenuse (the longest side, opposite to the 90° angle). Lines drawn along the X and Y-axes complete the other sides of the triangle, whose lengths can be found by finding the change in X and change in Y between the two points. We then use the Pythagorean theorem to find the length of the hypotenuse, which is the distance between the two points. If you didn't quite get that, the diagram below should help:
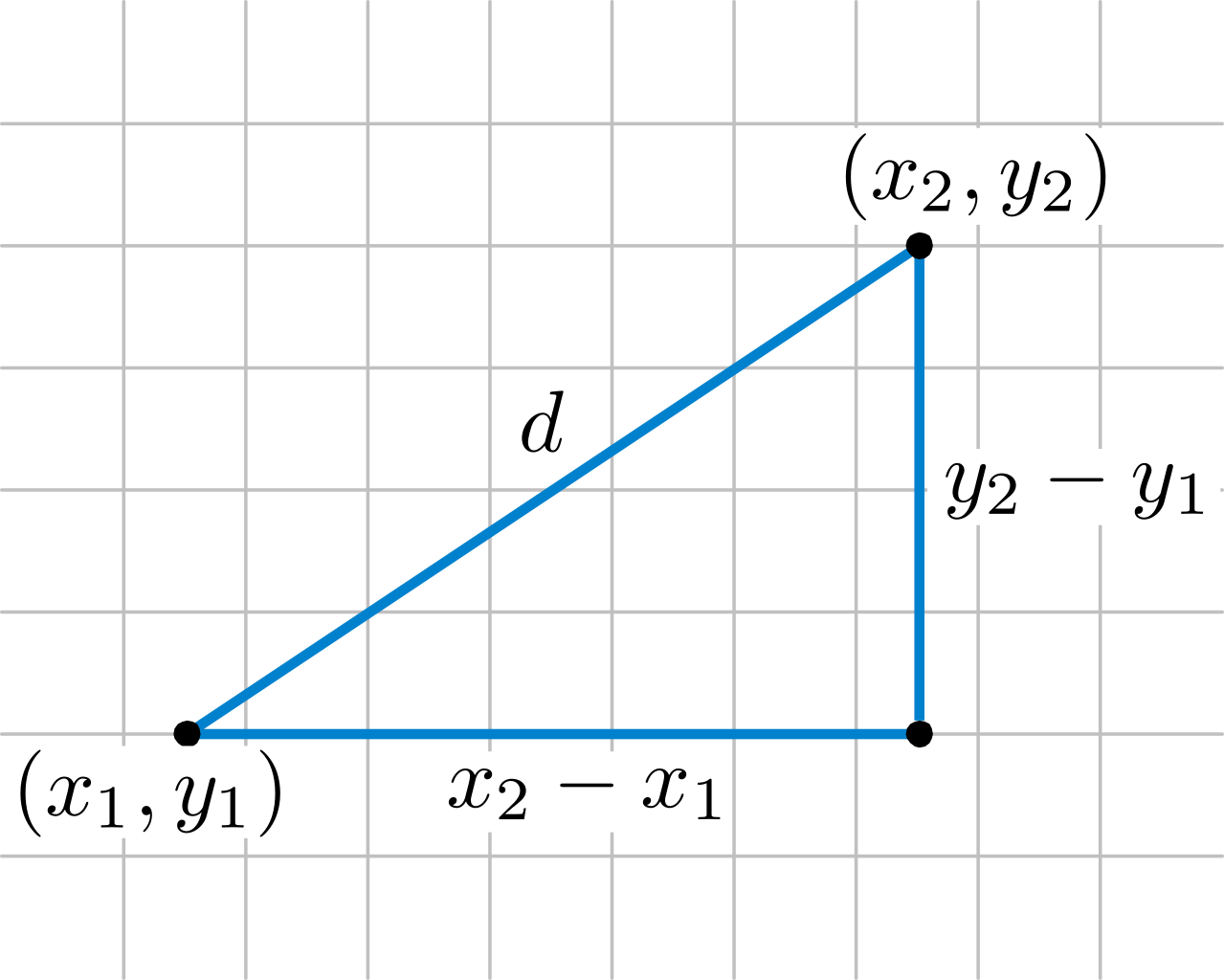
Image credit: `By Jim.belk, public domain, https://commons.wikimedia.org/wiki/File:Distance_Formula.svg`
Thus, using the Pythagorean theorem, the equation for the length of `d` would be:
`d = sqrt((x2 - x1)^2 + (y2 - y1)^2)`
## Sources and more info:
- https://www.mathsisfun.com/algebra/distance-2-points.html
---
<p align="center">
A massive collaborative effort by <a href="https://github.com/OpenGenus/cosmos">OpenGenus Foundation</a>
</p>
---
|
code/computational_geometry/src/distance_between_points/distance_between_points.c | #include <stdio.h>
#include <math.h>
struct Point {
double x;
double y;
};
double distanceBetweenPoints(Point a, Point b) {
return sqrt(pow(b.x - a.x, 2) + pow(b.y - a.y, 2));
}
int main() {
Point a, b;
printf("First point (x y): ");
scanf("%lg %lg", &a.x, &a.y);
printf("Second point (x y): ");
scanf("%lg %lg", &b.x, &b.y);
printf("%lg", distanceBetweenPoints(a, b));
return 0;
}
|
code/computational_geometry/src/distance_between_points/distance_between_points.cpp | #include <iostream>
#include <cmath>
typedef std::pair<double, double> point;
#define x first
#define y second
double calcDistance (point a, point b)
{
return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2));
}
int main ()
{
point a, b, c;
std::cin >> a.x >> a.y >> b.x >> b.y;
std::cout << calcDistance(a, b);
}
|
code/computational_geometry/src/distance_between_points/distance_between_points.go | package main
// Part of Cosmos by OpenGenus Foundation
import (
"fmt"
"math"
)
type vector struct {
x, y float64
}
func calculateDistance(a, b vector) float64 {
return math.Sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y))
}
func main() {
a := vector{x: 5, y: 5}
b := vector{x: 5, y: 10}
// 5
fmt.Println(calculateDistance(a, b))
a = vector{x: 2, y: 4}
b = vector{x: 4, y: -4}
// 8.246
fmt.Println(calculateDistance(a, b))
}
|
code/computational_geometry/src/distance_between_points/distance_between_points.java | import java.lang.Math;
public class DistanceBetweenPoints {
public static void main(String []args){
// input points {x,y}
int[] pointA = {0,1};
int[] pointB = {0,4};
double result = Math.sqrt(Math.pow((pointB[0] - pointA[0]), 2) + Math.pow((pointB[1] - pointA[1]), 2));
System.out.println(result);
}
}
|
code/computational_geometry/src/distance_between_points/distance_between_points.js | function distanceBetweenPoints(x1, x2, y1, y2) {
return Math.hypot(x1, x2, y1, y2);
}
console.log(distanceBetweenPoints(0, 3, 0, 4));
|
code/computational_geometry/src/distance_between_points/distance_between_points.py | def calc_distance(x1, y1, x2, y2):
return (((x1 - x2) ** 2) + ((y1 - y2) ** 2)) ** 0.5
x1 = float(input("Enter X coordinate of point 1: "))
y1 = float(input("Enter Y coordinate of point 1: "))
x2 = float(input("Enter X coordinate of point 2: "))
y2 = float(input("Enter Y coordinate of point 2: "))
print("Distance between (x1, y1) and (x2, y2) : " + str(calc_distance(x1, y1, x2, y2)))
|
code/computational_geometry/src/distance_between_points/distance_between_points.rs | struct Point {
x: f64,
y: f64
}
impl Point {
fn distance_to(&self, b: &Point) -> f64 {
((self.x - b.x) * (self.x - b.x) + (self.y - b.y) * (self.y - b.y)).sqrt()
}
}
#[test]
fn test_point_distance() {
// Make 2 points
// (0,0), (3,4), distance should be 5
let a = Point { x: 0.0, y: 0.0 };
let b = Point { x: 3.0, y: 4.0 };
assert_eq!(a.distance_to(&b), 5.0);
}
|
code/computational_geometry/src/graham_scan/graham_scan.cpp | /* Part of Cosmos by OpenGenus Foundation */
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
struct point
{
double x, y;
point(double x, double y) : x(x), y(y)
{
}
point()
{
}
};
// custom compare for sorting points
bool cmp(point a, point b)
{
return a.x < b.x || (a.x == b.x && a.y < b.y);
}
// check clockwise orientation of points
bool cw(point a, point b, point c)
{
return a.x * (b.y - c.y) + b.x * (c.y - a.y) + c.x * (a.y - b.y) < 0;
}
// check counter-clockwise orientation of points
bool ccw(point a, point b, point c)
{
return a.x * (b.y - c.y) + b.x * (c.y - a.y) + c.x * (a.y - b.y) > 0;
}
// graham scan with Andrew improvements
void convex_hull(vector<point> &points)
{
if (points.size() == 1)
return;
sort(points.begin(), points.end(), &cmp);
point p1 = points[0], p2 = points.back();
vector<point> up, down;
up.push_back(p1);
down.push_back(p1);
for (size_t i = 1; i < points.size(); ++i)
{
if (i == points.size() - 1 || cw(p1, points[i], p2))
{
while (up.size() >= 2 && !cw(up[up.size() - 2], up[up.size() - 1], points[i]))
up.pop_back();
up.push_back(points[i]);
}
if (i == points.size() - 1 || ccw(p1, points[i], p2))
{
while (down.size() >= 2 &&
!ccw(down[down.size() - 2], down[down.size() - 1], points[i]))
down.pop_back();
down.push_back(points[i]);
}
}
cout << "Convex hull is:" << endl;
for (size_t i = 0; i < up.size(); ++i)
cout << "x: " << up[i].x << " y: " << up[i].y << endl;
for (int i = down.size() - 2; i > 0; --i)
cout << "x: " << down[i].x << " y: " << down[i].y << endl;
}
int main()
{
int n;
cout << "Enter number of points followed by points" << endl;
cin >> n;
vector<point> points(n);
for (int i = 0; i < n; i++)
cin >> points[i].x >> points[i].y;
convex_hull(points);
return 0;
}
|
code/computational_geometry/src/graham_scan/graham_scan.java | import java.util.*;
public class GrahamScan {
public static class Point {
private final int x;
private final int y;
private final int pos;
public Point(final int x, final int y, final int p) {
this.x = x;
this.y = y;
this.pos = p;
}
}
public static double dist(Point p1, Point p2) {
return Math.sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}
public static int ccw(Point a, Point b, Point c) {
int cross = ((b.x - a.x) * (c.y - a.y)) - ((b.y - a.y) * (c.x - a.x));
if(cross > 0) {
return -1;
} else if(cross < 0) {
return 1;
} else {
return 0;
}
}
public static Point getBottomMostLeftPoint(List<Point> points) {
Point lowest = points.get(0);
for(int i = 1; i < points.size(); i++) {
if(points.get(i).y < lowest.y || (points.get(i).y == lowest.y && points.get(i).x < lowest.x)) {
lowest = points.get(i);
}
}
return lowest;
}
public static void sortByPolarAngle(ArrayList<Point> points) {
final Point bottomMostLeft = getBottomMostLeftPoint(points);
Collections.sort(points, new Comparator<Point>() {
@Override
public int compare(Point a, Point b) {
double angleA = Math.atan2(a.y - bottomMostLeft.y, a.x - bottomMostLeft.x);
double angleB = Math.atan2(b.y - bottomMostLeft.y, b.x - bottomMostLeft.x);
if(angleA < angleB) {
return 1;
} else if(angleA > angleB) {
return -1;
} else {
if(dist(a, bottomMostLeft) < dist(b, bottomMostLeft)) {
return 1;
} else {
return -1;
}
}
}
});
}
public static ArrayList<Point> getConvexHull(ArrayList<Point> points) {
if(points.size() == 1) {
return points;
}
sortByPolarAngle(points);
Collections.reverse(points);
ArrayList<Point> hull = new ArrayList<>();
hull.add(points.get(0));
hull.add(points.get(1));
for(int i = 2; i < points.size(); i++) {
Point c = points.get(i);
Point b = hull.get(hull.size()-1);
Point a = hull.get(hull.size()-2);
switch (ccw(a, b, c)) {
case -1:
hull.add(c);
break;
case 1:
hull.remove(hull.size()-1);
i--;
break;
case 0:
hull.remove(hull.size()-1);
hull.add(c);
break;
}
}
hull.add(hull.get(0));
return hull;
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
ArrayList<Point> points = new ArrayList<>();
for (int i = 0; i < N; i++) {
int x = in.nextInt(), y = in.nextInt();
Point p = new Point(x, y, i + 1);
points.add(p);
}
Collections.sort(points, new Comparator<Point>() {
@Override
public int compare(Point o1, Point o2) {
if (o1.x == o2.x) {
return o1.y - o2.y;
} else {
return o1.x - o2.x;
}
}
});
ArrayList<Point> temp = new ArrayList<>();
temp.add(points.get(0));
for(int i = 1; i < N; i++) {
if(points.get(i).x != points.get(i-1).x || points.get(i).y != points.get(i-1).y) {
temp.add(points.get(i));
}
}
points = temp;
points = getConvexHull(points);
double ans = 0;
for (int i = 1; i < points.size(); i++) {
ans += dist(points.get(i - 1), points.get(i));
}
System.out.println(ans);
System.out.println("AntiClockwise starting from Bottom-most left point: ");
for(int i = 0; i < points.size()-1; i++) {
System.out.print(points.get(i).pos + " ");
}
if(points.size() == 1) {
System.out.print("1");
}
System.out.println("\n");
}
}
|
code/computational_geometry/src/graham_scan/graham_scan.py | from functools import cmp_to_key
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
def orientation(p1, p2, p3):
# Slope of line segment (p1, p2): σ = (y2 - y1)/(x2 - x1)
# Slope of line segment (p2, p3): τ = (y3 - y2)/(x3 - x2)
#
# If σ > τ, the orientation is clockwise (right turn)
#
# Using above values of σ and τ, we can conclude that,
# the orientation depends on sign of below expression:
#
# (y2 - y1)*(x3 - x2) - (y3 - y2)*(x2 - x1)
#
# Above expression is negative when σ < τ, i.e., counterclockwise
val = (float(p2.y - p1.y) * (p3.x - p2.x)) - (float(p2.x - p1.x) * (p3.y - p2.y))
if val > 0:
# Clockwise orientation
return 1
elif val < 0:
# Counterclockwise orientation
return 2
else:
# Collinear orientation
return 0
def distSquare(p1, p2):
return ((p1.x - p2.x) ** 2 +
(p1.y - p2.y) ** 2)
def compare(p1, p2):
# Find orientation
o = orientation(p0, p1, p2)
if o == 0:
if distSquare(p0, p2) >= distSquare(p0, p1):
return -1
else:
return 1
else:
if o == 2:
return -1
else:
return 1
def ConvexHull(points, n):
# Find the bottommost point
ymin = points[0].y
minimum = 0
for i in range(1, n):
y = points[i].y
# Pick the bottom-most or choose the left
# most point in case of tie
if ((y < ymin) or
(ymin == y and points[i].x < points[minimum].x)):
ymin = points[i].y
minimum = i
# Place the bottom-most point at first position
points[0], points[minimum] = points[minimum], points[0]
# Sort n-1 points with respect to the first point.
# A point p1 comes before p2 in sorted output if p2
# has larger polar angle (in counterclockwise
# direction) than p1
p0 = points[0]
sorted_points = sorted(points, key=cmp_to_key(compare))
# If two or more points make same angle with p0,
# Remove all but the one that is farthest from p0
# Remember that, in above sorting, our criteria was
# to keep the farthest point at the end when more than
# one points have same angle.
m = 1 # Initialize size of modified array
for i in range(1, n):
# Keep removing i while angle of i and i+1 is same
# with respect to p0
while ((i < n - 1) and
(orientation(p0, sorted_points[i], sorted_points[i + 1]) == 0)):
i += 1
sorted_points[m] = sorted_points[i]
m += 1 # Update size of modified array
# If modified array of points has less than 3 points,
# convex hull is not possible
if m < 3:
return
S = [sorted_points[0], sorted_points[1], sorted_points[2]]
# Process remaining n-3 points
for i in range(3, m):
# Keep removing top while the angle formed by
# points next-to-top, top, and points[i] makes
# a non-left turn
while ((len(S) > 1) and
(orientation(S[-2], S[-1], sorted_points[i]) != 2)):
S.pop()
S.append(sorted_points[i])
S2 = S.copy()
# Now stack has the output points,
# print contents of stack
while S:
p = S[-1]
print("(" + str(p.x) + ", " + str(p.y) + ")")
S.pop()
return S2
def visualize(points, convex_hull_points):
from matplotlib import pyplot as plt
import numpy as np
x_co = []
y_co = []
for point in points:
x_co.append(point.x)
y_co.append(point.y)
plt.scatter(np.array(x_co), np.array(y_co))
convex_x_co = []
convex_y_co = []
for point in convex_hull_points:
convex_x_co.append(point.x)
convex_y_co.append(point.y)
plt.plot(np.array(convex_x_co), np.array(convex_y_co))
plt.show()
if __name__ == "__main__":
n = int(input("Enter number of points followed by points: "))
points = [] # List of Points
p0 = Point(0, 0)
for i in range(n):
x, y = list(map(int, input().split()))
points.append(Point(x, y))
convex_hull_points = ConvexHull(points, n)
# Optional, please comment this line if you don't want to visualize
visualize(points, convex_hull_points)
|
code/computational_geometry/src/graham_scan/graham_scan2.cpp | #include <iostream>
#include <stack>
#include <stdlib.h>
using namespace std;
// Part of Cosmos by OpenGenus Foundation
// A C++ program to find convex hull of a set of points.
struct Point
{
int x, y;
};
// A globle point needed for sorting points with reference
// to the first point Used in compare function of qsort()
Point p0;
// A utility function to find next to top in a stack
Point nextToTop(stack<Point> &S)
{
Point p = S.top();
S.pop();
Point res = S.top();
S.push(p);
return res;
}
// A utility function to swap two points
int swap(Point &p1, Point &p2)
{
Point temp = p1;
p1 = p2;
p2 = temp;
}
// A utility function to return square of distance
// between p1 and p2
int distSq(Point p1, Point p2)
{
return (p1.x - p2.x) * (p1.x - p2.x) +
(p1.y - p2.y) * (p1.y - p2.y);
}
// To find orientation of ordered triplet (p, q, r).
// The function returns following values
// 0 --> p, q and r are colinear
// 1 --> Clockwise
// 2 --> Counterclockwise
int orientation(Point p, Point q, Point r)
{
int val = (q.y - p.y) * (r.x - q.x) -
(q.x - p.x) * (r.y - q.y);
if (val == 0)
return 0; // colinear
return (val > 0) ? 1 : 2; // clock or counterclock wise
}
// A function used by library function qsort() to sort an array of
// points with respect to the first point
int compare(const void *vp1, const void *vp2)
{
Point *p1 = (Point *)vp1;
Point *p2 = (Point *)vp2;
// Find orientation
int o = orientation(p0, *p1, *p2);
if (o == 0)
return (distSq(p0, *p2) >= distSq(p0, *p1)) ? -1 : 1;
return (o == 2) ? -1 : 1;
}
// Prints convex hull of a set of n points.
void convexHull(Point points[], int n)
{
// Find the bottommost point
int ymin = points[0].y, min = 0;
for (int i = 1; i < n; i++)
{
int y = points[i].y;
// Pick the bottom-most or chose the left
// most point in case of tie
if ((y < ymin) || (ymin == y &&
points[i].x < points[min].x))
ymin = points[i].y, min = i;
}
// Place the bottom-most point at first position
swap(points[0], points[min]);
// Sort n-1 points with respect to the first point.
// A point p1 comes before p2 in sorted ouput if p2
// has larger polar angle (in counterclockwise
// direction) than p1
p0 = points[0];
qsort(&points[1], n - 1, sizeof(Point), compare);
// If two or more points make same angle with p0,
// Remove all but the one that is farthest from p0
// Remember that, in above sorting, our criteria was
// to keep the farthest point at the end when more than
// one points have same angle.
int m = 1; // Initialize size of modified array
for (int i = 1; i < n; i++)
{
// Keep removing i while angle of i and i+1 is same
// with respect to p0
while (i < n - 1 && orientation(p0, points[i],
points[i + 1]) == 0)
i++;
points[m] = points[i];
m++; // Update size of modified array
}
// If modified array of points has less than 3 points,
// convex hull is not possible
if (m < 3)
return;
// Create an empty stack and push first three points
// to it.
stack<Point> S;
S.push(points[0]);
S.push(points[1]);
S.push(points[2]);
// Process remaining n-3 points
for (int i = 3; i < m; i++)
{
// Keep removing top while the angle formed by
// points next-to-top, top, and points[i] makes
// a non-left turn
while (orientation(nextToTop(S), S.top(), points[i]) != 2)
S.pop();
S.push(points[i]);
}
// Now stack has the output points, print contents of stack
while (!S.empty())
{
Point p = S.top();
cout << "(" << p.x << ", " << p.y << ")" << endl;
S.pop();
}
}
// Driver program to test above functions
int main()
{
Point points[] = {{0, 3}, {1, 1}, {2, 2}, {4, 4},
{0, 0}, {1, 2}, {3, 1}, {3, 3}};
int n = sizeof(points) / sizeof(points[0]);
convexHull(points, n);
return 0;
}
|
code/computational_geometry/src/halfplane_intersection/halfplane_intersection.cpp | #include <cmath>
#include <iostream>
#include <vector>
using namespace std;
const double INF = 1e9;
const double EPS = 1e-8;
class Point {
public:
double x, y;
Point()
{
}
Point(double x, double y) : x(x), y(y)
{
}
bool operator==(const Point &other) const
{
return abs(x - other.x) < EPS && abs(y - other.y) < EPS;
}
Point operator-(const Point &a) const
{
return Point(x - a.x, y - a.y);
}
double operator^(const Point &a) const
{
return x * a.y - a.x * y;
}
void scan()
{
cin >> x >> y;
}
void print() const
{
cout << x << " " << y << "\n";
}
};
class Line {
public:
double a, b, c;
Line()
{
}
Line(double a, double b, double c) : a(a), b(b), c(c)
{
}
Line(const Point &A, const Point &B) : a(A.y - B.y), b(B.x - A.x),
c(A.x * (B.y - A.y) + A.y * (A.x - B.x))
{
}
bool operator==(const Line &other) const
{
return a == other.a && b == other.b && c == other.c;
}
bool contains_point(const Point &A) const
{
return a * A.x + b * A.y + c == 0;
}
bool intersects(const Line &l) const
{
return !(a * l.b == b * l.a);
}
Point intersect(const Line &l) const
{
return Point(-(c * l.b - l.c * b) / (a * l.b - l.a * b),
-(a * l.c - l.a * c) / (a * l.b - l.a * b));
}
};
class Segment {
private:
Point A, B;
public:
Segment()
{
}
Segment(Point A, Point B) : A(A), B(B)
{
}
bool intersects(const Line &l) const
{
return l.intersects(Line(A, B)) &&
l.intersect(Line(A, B)).x <= max(A.x, B.x) + EPS &&
l.intersect(Line(A, B)).x >= min(A.x, B.x) - EPS &&
l.intersect(Line(A, B)).y <= max(A.y, B.y) + EPS &&
l.intersect(Line(A, B)).y >= min(A.y, B.y) - EPS;
}
double length2() const
{
return (A - B).x * (A - B).x + (A - B).y * (A - B).y;
}
double length() const
{
return sqrt(length2());
}
};
class HalfPlane {
private:
double a, b, c;
public:
HalfPlane()
{
}
HalfPlane(Line l, Point A)
{
if (l.a * A.x + l.b * A.y + l.c < 0)
{
a = -l.a;
b = -l.b;
c = -l.c;
}
else
{
a = l.a;
b = l.b;
c = l.c;
}
}
bool contains_point(const Point &p) const
{
return a * p.x + b * p.y + c >= 0;
}
Line line() const
{
return Line(a, b, c);
}
};
class HalfPlaneIntersector {
private:
vector <Point> points;
public:
HalfPlaneIntersector()
{
points.push_back(Point(-INF, INF));
points.push_back(Point(INF, INF));
points.push_back(Point(INF, -INF));
points.push_back(Point(-INF, -INF));
}
void intersect(const HalfPlane &h)
{
vector <Point> result;
for (unsigned int i = 0; i < points.size(); i++)
{
Line a = Line(points[i], points[(i + 1) % points.size()]);
Segment a_seg = Segment(points[i], points[(i + 1) % points.size()]);
if (h.contains_point(points[i]))
result.push_back(points[i]);
if (a_seg.intersects(h.line()))
result.push_back(a.intersect(h.line()));
}
points = result;
}
double perimeter() const
{
double res = 0;
for (unsigned int i = 0; i < points.size(); i++)
res += Segment(points[i], points[(i + 1) % points.size()]).length();
return res;
}
};
// Calculate perimeter of 2 triangle intersection for examle.
int main()
{
HalfPlaneIntersector hpi;
for (int i = 0; i < 2; i++)
{
Point p1, p2, p3;
p1.scan();
p2.scan();
p3.scan();
hpi.intersect(HalfPlane(Line(p1, p2), p3));
hpi.intersect(HalfPlane(Line(p1, p3), p2));
hpi.intersect(HalfPlane(Line(p2, p3), p1));
}
cout << hpi.perimeter();
}
|
code/computational_geometry/src/jarvis_march/README.md | # Jarvis March Algorithm
## python version 1.0
How to start?
* Run "python jarvis_march.py" and see what happens (hint: MAGIC)
* Change the points in the main function.
These are some results:
#### 10 random points
<p align="center">
<img src="https://i.imgur.com/VP3VDuG.png" width="350"/>
<img src="https://i.imgur.com/YVyaEaW.png" width="350"/>
</p>
#### 100 random points
<p align="center">
<img src="https://i.imgur.com/Dvvy5De.png" width="350"/>
<img src="https://i.imgur.com/IHdmDjv.png" width="350"/>
</p>
#### 1000 random points
<p align="center">
<img src="https://i.imgur.com/hcuFKzi.png" width="350"/>
<img src="https://i.imgur.com/z8YGVEy.png" width="350"/>
</p>
### Useful Links for further reading:
* [jarvis_march on youtube](https://www.youtube.com/watch?v=Vu84lmMzP2o) - great explenation (demo+code)
* [convex hull + jarvis theory](http://jeffe.cs.illinois.edu/teaching/373/notes/x05-convexhull.pdf) - Theoretical explenation
* [Gift wrapping algorithm](https://en.wikipedia.org/wiki/Gift_wrapping_algorithm) - wikipedia overview
|
code/computational_geometry/src/jarvis_march/jarvis_march.cpp | #include <iostream>
#include <vector>
#include <cmath>
using namespace std;
struct Point
{
int x;
int y;
int pos;
Point(int x, int y, int p)
{
this->x = x;
this->y = y;
this->pos = p;
}
};
int orientation(Point p, Point q, Point r)
{
int cross = (q.y - p.y) * (r.x - q.x) - (q.x - p.x) * (r.y - q.y);
if (cross == 0)
return 0;
return (cross > 0) ? 1 : -1;
}
vector<Point> getConvexHull(vector<Point> points)
{
if (points.size() < 3)
return points;
int left = 0;
for (size_t i = 1; i < points.size(); i++)
if (points[i].x < points[left].x)
left = i;
// Starting from left move counter-clockwise
vector<Point> hull;
int tail = left, middle;
do {
middle = (tail + 1) % points.size();
for (size_t i = 0; i < points.size(); i++)
if (orientation(points[tail], points[i], points[middle]) == -1)
middle = i;
hull.push_back(points[middle]);
tail = middle;
} while (tail != left);
return hull;
}
double dist(Point p1, Point p2)
{
return sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
}
int main()
{
int N;
cin >> N;
vector<Point> points;
for (int i = 0; i < N; i++)
{
int x, y;
cin >> x >> y;
points.push_back(Point(x, y, i + 1));
}
vector<Point> result = getConvexHull(points);
result.push_back(result[0]);
double ans = 0;
for (size_t i = 1; i < result.size(); i++)
ans += dist(result[i], result[i - 1]);
cout << ans << '\n';
cout << "Points lying on hull\n";
for (size_t i = 0; i < result.size(); i++)
cout << result[i].pos << ' ';
}
|
code/computational_geometry/src/jarvis_march/jarvis_march.py | import matplotlib.pyplot as plt
import numpy as np
import math
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
def equal(self, pt):
return self.x == pt.x and self.y == pt.y
def __str__(self):
return "(" + str(self.x) + "," + str(self.y) + ")"
def left_most_point(pts):
if not isinstance(pts, list):
return False
curr = pts[0]
for pt in pts[1:]:
if pt.x < curr.x or (pt.x == curr.x and pt.y < curr.y):
curr = pt
return curr
def cross_product(p, p1, p2):
return (p.y - p2.y) * (p.x - p1.x) - (p.y - p1.y) * (p.x - p2.x)
def distance(p, p1, p2):
return math.hypot(p.x - p1.x, p.y - p1.y) - math.hypot(p.x - p2.x, p.y - p2.y)
def iter(pts):
colinear = list()
curr_pt = left_most_point(pts)
convex_list = [curr_pt]
for pt1 in pts:
if curr_pt.equal(pt1):
continue
target = pt1
for pt2 in pts:
if pt2.equal(target) or pt2.equal(curr_pt):
continue
res = cross_product(curr_pt, target, pt2)
if res > 0:
colinear = list()
target = pt2
elif res == 0:
if distance(curr_pt, target, pt2) > 0:
if pt2 not in colinear:
colinear.append(pt2)
else:
if target not in colinear:
colinear.append(target)
target = pt2
if target not in convex_list:
convex_list.append(target)
for colinear_pt in colinear:
if colinear_pt not in convex_list:
convex_list.append(colinear_pt)
curr_pt = target
return convex_list
def main():
pts = [Point(x, y) for x, y in np.random.rand(100, 2)]
convex_lst = iter(pts)
len_convex_pts = len(convex_lst)
print(*convex_lst)
plt.plot(
[p.x for p in convex_lst] + [convex_lst[0].x],
[p.y for p in convex_lst] + [convex_lst[0].y],
"-",
)
plt.scatter([p.x for p in pts], [p.y for p in pts], color="red")
plt.title(
"Jarvis March Algorithm (Total "
+ str(len_convex_pts)
+ "/"
+ str(len(pts))
+ " points)"
)
plt.grid()
plt.show()
if __name__ == "__main__":
main()
|
code/computational_geometry/src/jarvis_march/jarvis_march2.cpp | // A C++ program to find convex hull of a set of points
#include <bits/stdc++.h>
using namespace std;
struct Point // Structure to store the co-ordinates of every point
{
int x, y;
};
// To find orientation of ordered triplet (p, q, r).
// The function returns following values
// 0 --> p, q and r are colinear
// 1 --> Clockwise
// 2 --> Counterclockwise
int orientation(Point p, Point q, Point r)
{
/*
* Finding slope ,s = (y2 - y1)/(x2 - x1) ;
* s1 = (y3 - y2)/(x3 - x2) ;
* if s == s1 points are collinear
* s < s1 orientation towards left (left turn)
* s > s1 orientation towards right (right turn)
*/
int val = (q.y - p.y) * (r.x - q.x) -
(q.x - p.x) * (r.y - q.y);
if (val == 0)
return 0; // colinear
return (val > 0) ? 1 : 2; // clock or counterclock wise
}
// Prints convex hull of a set of n points.
void convexHull(Point points[], int n)
{
// There must be at least 3 points
if (n < 3)
return;
// Initialize Result
vector<Point> hull;
// Find the leftmost point
int l = 0;
for (int i = 1; i < n; i++)
if (points[i].x < points[l].x)
l = i;
// Start from leftmost point, keep moving counterclockwise
// until reach the start point again. This loop runs O(h)
// times where h is number of points in result or output.
int p = l, q;
do
{
// Add current point to result
hull.push_back(points[p]);
// Search for a point 'q' such that orientation(p, x,
// q) is counterclockwise for all points 'x'. The idea
// is to keep track of last visited most counterclock-
// wise point in q. If any point 'i' is more counterclock-
// wise than q, then update q.
q = (p + 1) % n;
for (int i = 0; i < n; i++)
// If i is more counterclockwise than current q, then
// update q
if (orientation(points[p], points[i], points[q]) == 2)
q = i;
// Now q is the most counterclockwise with respect to p
// Set p as q for next iteration, so that q is added to
// result 'hull'
p = q;
} while (p != l); // While we don't come to first point
// Print Result
for (int i = 0; i < hull.size(); i++)
cout << "(" << hull[i].x << ", "
<< hull[i].y << ")\n";
}
// Driver program to test above functions
int main()
{
Point points[] = {{0, 3}, {2, 2}, {1, 1}, {2, 1},
{3, 0}, {0, 0}, {3, 3}};
int n = sizeof(points) / sizeof(points[0]);
convexHull(points, n);
return 0;
}
|
code/computational_geometry/src/liang_barsky_algo/liang_barsky_algo.c | /* Header files included */
#include <stdio.h>
#include <conio.h>
#include <graphics.h>
int
main()
{
int gd = DETECT, gm;
/*
* x1, x2, y1 & y2 are line coordinates
* xmax, xmin, ymax & ymin are window's lower and upper corner coordinates
* xx1, yy1, xx2 & yy2 are the new coordinates of clipped line
*/
int x1, y1, x2, y2;
int xmax, xmin, ymax, ymin;
int xx1, yy1, xx2, yy2;
int dx, dy, i;
int p[4], q[4];
float t1, t2, t[4];
initgraph (& gd, & gm, "C:\\TC\\BGI");
/* Enter the coordinates for window*/
printf ("Enter the lower co-ordinates of window");
scanf ("%d", &xmin, &ymin);
printf ("Enter the upper co-ordinates of window");
scanf ("%d", &xmax, &ymax);
/* Graphics function to draw rectangle/clipping window */
setcolor (RED);
rectangle (xmin, ymin, xmax, ymax);
/* Enter the coordinates of line */
printf ("Enter x1:");
scanf("%d", &x1);
printf("Enter y1:");
scanf("%d", &y1);
printf("Enter x2:");
scanf("%d", &x2);
printf("Enter y2:");
scanf("%d", &y2);
/* Graphics Function to draw line */
line (x1, y1, x2, y2);
dx = x2 - x1;
dy = y2 - y1;
p[0] = - dx;
p[1] = dx;
p[2] = - dy;
p[3] = dy;
q[0] = x1 - xmin;
q[1] = xmax - x1;
q[2] = y1 - ymin;
q[3] = ymax - y1;
for (i=0; i < 4; i++)
{
if (p[i] != 0) {
t[i] = (float) q[i] / p[i];
}
else {
if (p[i] == 0 && q[i] < 0)
printf ("line completely outside the window");
else
if (p[i] == 0 && q[i] >= 0)
printf ("line completely inside the window");
}
}
if (t[0] > t[2])
t1 = t[0];
else
t1 = t[2];
if (t[1] < t[3])
t2 = t[1];
else
t2 = t[3];
if (t1 < t2) {
xx1 = x1 + t1 * dx;
xx2 = x1 + t2 * dx;
yy1 = y1 + t1 * dy;
yy2 = y1 + t2 * dy;
/* Draw the clipped line */
printf ("line after clipping:");
setcolor (WHITE);
line (xx1, yy1, xx2, yy2);
}
else
printf ("line lies out of the window");
getch();
return (0);
}
|
code/computational_geometry/src/liang_barsky_algo/liang_barsky_algo.cpp | // Header files included
#include <iostream.h>
#include <conio.h>
#include <graphics.h>
using namespace std;
int main()
{
int gd = DETECT, gm;
/*
* x1, x2, y1 & y2 are line coordinates
* xmax, xmin, ymax & ymin are window's lower and upper corner coordinates
* xx1, yy1, xx2 & yy2 are the new coordinates of clipped line
*/
int x1, y1, x2, y2;
int xmax, xmin, ymax, ymin;
int xx1, yy1, xx2, yy2;
int dx, dy, i;
int p[4], q[4];
float t1, t2, t[4];
initgraph (& gd, & gm, "C:\\TC\\BGI");
// Enter the coordinates for window
cout << "Enter the lower co-ordinates of window";
cin >> xmin >> ymin;
cout << "Enter the upper co-ordinates of window";
cin >> xmax >> ymax;
// Graphics function to draw rectangle/clipping window
setcolor (RED);
rectangle (xmin, ymin, xmax, ymax);
// Enter the coordinates of line
cout << "Enter x1:";
cin >> x1;
cout << "Enter y1:";
cin >> y1;
cout << "Enter x2:";
cin >> x2;
cout << "Enter y2:";
cin >> y2;
// Graphics Function to draw line
line (x1, y1, x2, y2);
dx = x2 - x1;
dy = y2 - y1;
p[0] = - dx;
p[1] = dx;
p[2] = - dy;
p[3] = dy;
q[0] = x1 - xmin;
q[1] = xmax - x1;
q[2] = y1 - ymin;
q[3] = ymax - y1;
for (i=0; i < 4; i++)
{
if (p[i] != 0)
{
t[i] = (float) q[i] / p[i];
}
else
{
if (p[i] == 0 && q[i] < 0)
cout << "line completely outside the window";
else
if (p[i] == 0 && q[i] >= 0)
cout << "line completely inside the window";
}
}
if (t[0] > t[2])
t1 = t[0];
else
t1 = t[2];
if (t[1] < t[3])
t2 = t[1];
else
t2 = t[3];
if (t1 < t2)
{
xx1 = x1 + t1 * dx;
xx2 = x1 + t2 * dx;
yy1 = y1 + t1 * dy;
yy2 = y1 + t2 * dy;
cout << "line after clipping:";
setcolor (WHITE);
line (xx1, yy1, xx2, yy2);
}
else
cout << "line lies out of the window";
getch();
return (0);
}
|
code/computational_geometry/src/mandelbrot_fractal/mandelbrot_fractal.py | import numpy
import matplotlib.pyplot as plt
def mandelbrot(Re, Im, max_iter):
c = complex(Re, Im)
z = 0.0j
for i in range(max_iter):
z = z * z + c
if (z.real * z.real + z.imag * z.imag) >= 4:
return i
return max_iter
columns = 2000
rows = 2000
result = numpy.zeros([rows, columns])
for row_index, Re in enumerate(numpy.linspace(-2, 1, num=rows)):
for column_index, Im in enumerate(numpy.linspace(-1, 1, num=columns)):
result[row_index, column_index] = mandelbrot(Re, Im, 100)
plt.figure(dpi=100)
plt.imshow(result.T, cmap="plasma", interpolation="bilinear", extent=[-2, 1, -1, 1])
plt.xlabel("Re")
plt.ylabel("Im")
plt.show()
|
code/computational_geometry/src/quick_hull/README.md | # Quickhull
For theoretical background see [Quickhull](https://en.wikipedia.org/wiki/Quickhull).
Test data can be found in `test_data.csv`.
Example of convex hull of a set of points:

|
code/computational_geometry/src/quick_hull/quick_hull.cpp | #include <vector>
#include <iostream>
#include <cmath>
using namespace std;
struct vec2
{
float x, y;
vec2(float x, float y) : x(x), y(y)
{
}
vec2()
{
}
};
vector<vec2> input;
vector<vec2> output;
float lineToPointSupport(vec2 l1, vec2 l2, vec2 p)
{
return abs ((p.y - l1.y) * (l2.x - l1.x) -
(l2.y - l2.y) * (p.x - l1.x));
}
float dot(vec2 A, vec2 B)
{
return A.x * B.x + A.y * B.y;
}
void findHull(int a, int b)
{
float dy = input[b].y - input[a].y;
float dx = input[b].x - input[a].x;
vec2 normal(-dy, dx);
float biggestLinePointDistance = -1;
int c = 0;
for (size_t i = 0; i < input.size(); i++)
{
vec2 aToPoint(input[i].x - input[a].x, input[i].y - input[a].y);
if (dot(aToPoint, normal) < 0 || static_cast<int>(i) == a || static_cast<int>(i) == b)
continue;
float lineToPoint = lineToPointSupport(input[a], input[b], input[i]);
if (lineToPoint > biggestLinePointDistance)
{
c = i;
biggestLinePointDistance = lineToPoint;
}
}
if (biggestLinePointDistance == -1)
return;
output.push_back(input[c]);
findHull(a, c);
findHull(c, b);
}
void quickhull()
{
if (input.size() < 3)
return;
float mini = 0;
float maxi = 0;
for (size_t i = 0; i < input.size(); i++)
{
if (input[i].x < input[mini].x)
mini = i;
if (input[i].x > input[maxi].x)
maxi = i;
}
output.push_back(input[mini]);
output.push_back(input[maxi]);
findHull(mini, maxi);
findHull(maxi, mini);
}
int main()
{
//example set 1
input.push_back(vec2(5, 10));
input.push_back(vec2(10, 10));
input.push_back(vec2(7, 15));
input.push_back(vec2(7, 13));
//example set 2
// input.push_back(vec2(0, 15));
// input.push_back(vec2(10, 15));
// input.push_back(vec2(10, 20));
// input.push_back(vec2(0, 20));
// input.push_back(vec2(5, 17));
quickhull();
for (size_t i = 0; i < output.size(); i++)
cout << "x: " << output[i].x << "y: " << output[i].y << endl;
return 0;
}
|
code/computational_geometry/src/quick_hull/quick_hull.hs | -- Part of Cosmos by OpenGenus
-- Point in 2-D plane
data Point = Point {
x::Double,
y::Double
}
deriving (Show)
instance Eq Point where
(==) (Point x1 y1) (Point x2 y2) = x1 == x2 && y1 == y2
instance Ord Point where
compare (Point x1 y1) (Point x2 y2) = compare x1 x2
(<=) (Point x1 y1) (Point x2 y2) = x1 <= x2
pplus :: Point -> Point -> Point
pplus (Point x1 y1) (Point x2 y2) = Point (x1+x2) (y1+y2)
pminus :: Point -> Point -> Point
pminus (Point x1 y1) (Point x2 y2) = Point (x1-x2) (y1-y2)
-- Compute the dot product AB ⋅ BC
dot :: Point -> Point -> Double -- we use point type to represent vectors
dot (Point ab1 ab2) (Point bc1 bc2) = ab1 * bc1 + ab2 * bc2
-- Compute the cross product AB x AC
-- we use point type to represent vectors
cross :: Point -> Point -> Double -- 2 dimensional so return scalar
cross (Point ab1 ab2) (Point ac1 ac2) = ab1 * ac2 - ab2 * ac1
distance :: Point -> Point -> Double
distance (Point a1 a2) (Point b1 b2) = sqrt (d1*d1+d2*d2)
where d1 = a1 - b1
d2 = a2 - b2
quickHull :: [Point] -> [Point]
quickHull [] = []
quickHull l = trace ("A: " ++ show pA ++ " and B: " ++ show pB ++ "\n") $ pA : pB : findHull rhs pA pB ++ findHull lhs pB pA
where (lhs, rhs) = partition l pA pB
pA = maximum l
pB = minimum l
partition :: [Point] -> Point -> Point -> ([Point], [Point])
-- returns ([points on LHS of line AB], [points on RHS of line AB])
partition l pA pB = (partition' (\x -> snd x > 0) , partition' (\x -> snd x < 0))
where pointOPMap = zip l (map _ABCrossAP l)
_ABCrossAP p = (pB `pminus` pA) `cross` (p `pminus` pA)
partition' f = map fst (filter f pointOPMap)
-- Triangle PQM looks like this:
-- M
-- ·
-- · ·
-- S2 · · S1
-- · S0 ·
-- · ·
-- · · · · · · · ·
-- Q P
findHull :: [Point] -> Point -> Point -> [Point]
findHull [] _ _ = []
findHull s p q = trace ("M: " ++ show m ++ " P: " ++ show p ++ "Q: " ++ show q ++ "\n") $ m : findHull s1 p m ++ findHull s2 m q
where m = s!!fromJust (elemIndex max_dist dists) -- point of maximum distance on RHS of PQ
max_dist = maximum dists
dists = map (linePointDist p q) s
s1 = snd $ partition s p m -- rhs of line PM (outside triangle)
s2 = fst $ partition s q m -- lhs of line QM (outside triangle)
-- Compute the distance from line segment AB to C
linePointDist :: Point -> Point -> Point -> Double
linePointDist a b c | dot1 > 0 = distbc
| dot2 > 0 = distac
| otherwise = abs dist
where dot1 = dot (c `pminus` b) (b `pminus` a)
dot2 = dot (c `pminus` a) (a `pminus` b)
distbc = distance b c
distac = distance a c
dist = cross (b `pminus` a) (c `pminus` a) / distance a b
|
code/computational_geometry/src/quick_hull/quick_hull.java | /* Part of Cosmos by OpenGenus Foundation */
import java.util.ArrayList;
import java.util.Scanner;
public class quickHull {
public static class Point {
private final int x;
private final int y;
private final int pos;
public Point(final int x, final int y, final int p) {
this.x = x;
this.y = y;
this.pos = p;
}
}
public static double dist(Point p1, Point p2) {
return Math.sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}
public static Point getLeftMostBottomPoint(ArrayList<Point> points) {
Point result = points.get(0);
for(int i = 1; i < points.size(); i++) {
if(points.get(i).x < result.x || (points.get(i).x == result.x && points.get(i).y < result.y)) {
result = points.get(i);
}
}
return result;
}
public static Point getRightMostUpperPoint(ArrayList<Point> points) {
Point result = points.get(0);
for(int i = 1; i < points.size(); i++) {
if(points.get(i).x > result.x || (points.get(i).x == result.x && points.get(i).y > result.y)) {
result = points.get(i);
}
}
return result;
}
// Partition P with respect to line joining A and B
public static int partition(Point A, Point B, Point P) {
int cp1 = (B.x - A.x) * (P.y - A.y) - (B.y - A.y) * (P.x - A.x);
if (cp1 > 0) return 1;
else if (cp1 == 0) return 0;
else return -1;
}
// https://brilliant.org/wiki/distance-between-point-and-line/
public static int distance(Point A, Point B, Point C) {
return Math.abs((B.x - A.x) * (A.y - C.y) - (B.y - A.y) * (A.x - C.x));
}
public static ArrayList<Point> quickHull(ArrayList<Point> points) {
ArrayList<Point> convexHull = new ArrayList<Point>();
if (points.size() < 3) return (new ArrayList<Point> (points));
Point leftMostBottom = getLeftMostBottomPoint(points);
Point rightMostUpper = getRightMostUpperPoint(points);
points.remove(leftMostBottom);
points.remove(rightMostUpper);
convexHull.add(leftMostBottom);
convexHull.add(rightMostUpper);
ArrayList<Point> leftPart = new ArrayList<>();
ArrayList<Point> rightPart = new ArrayList<>();
for(int i = 0; i < points.size(); i++) {
Point p = points.get(i);
if(partition(leftMostBottom, rightMostUpper,p) == -1) {
leftPart.add(p);
} else if(partition(leftMostBottom, rightMostUpper, p) == 1) {
rightPart.add(p);
}
}
hullSet(leftMostBottom, rightMostUpper, rightPart, convexHull);
hullSet(rightMostUpper, leftMostBottom, leftPart, convexHull);
return convexHull;
}
public static void hullSet(Point a, Point b, ArrayList<Point> set, ArrayList<Point> hull) {
int insertPosition = hull.indexOf(b);
if (set.size() == 0) return;
if (set.size() == 1) {
Point p = set.get(0);
set.remove(p);
hull.add(insertPosition, p);
return;
}
int furthestDist = 0;
Point furthestPoint = null;
for (int i = 0; i < set.size(); i++) {
Point p = set.get(i);
int distance = distance(a, b, p);
if (distance > furthestDist) {
furthestDist = distance;
furthestPoint = p;
}
}
set.remove(furthestPoint);
hull.add(insertPosition, furthestPoint);
// Determine who's to the left of line joining a and furthestPoint
ArrayList<Point> leftSet = new ArrayList<Point>();
for (int i = 0; i < set.size(); i++) {
Point current = set.get(i);
if (partition(a, furthestPoint, current) == 1) {
leftSet.add(current);
}
}
hullSet(a, furthestPoint, leftSet, hull);
// Determine who's to the left of line joining furthestPoint and b
leftSet = new ArrayList<>();
for (int i = 0; i < set.size(); i++) {
Point current = set.get(i);
if (partition(furthestPoint, b, current) == 1) {
leftSet.add(furthestPoint);
}
}
hullSet(furthestPoint, b, leftSet, hull);
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
ArrayList<Point> points = new ArrayList<>();
for(int i = 0; i < N; i++) {
int x = in.nextInt(), y = in.nextInt();
points.add(new Point(x, y, i+1));
}
ArrayList<Point> hull = quickHull(points);
double ans = 0;
for(int i = 1; i < hull.size(); i++) {
ans += dist(hull.get(i), hull.get(i-1));
}
ans += dist(hull.get(0), hull.get(hull.size()-1));
if(hull.size() == 1) ans = 0;
System.out.println(ans);
System.out.println("Points on the hull are:");
for(Point p: hull) {
System.out.print(p.pos+" ");
}
}
}
|
code/computational_geometry/src/quick_hull/quick_hull2.cpp | #include <bits/stdc++.h>
using namespace std;
// Part of Cosmos by OpenGenus Foundation
// C++ program to implement Quick Hull algorithm to find convex hull.
// iPair is integer pairs
#define iPair pair<int, int>
// Stores the result (points of convex hull)
set<iPair> hull;
// Returns the side of point p with respect to line
// joining points p1 and p2.
int findSide(iPair p1, iPair p2, iPair p)
{
int val = (p.second - p1.second) * (p2.first - p1.first) -
(p2.second - p1.second) * (p.first - p1.first);
if (val > 0)
return 1;
if (val < 0)
return -1;
return 0;
}
// Returns the square of distance between
// p1 and p2.
int dist(iPair p, iPair q)
{
return (p.second - q.second) * (p.second - q.second) +
(p.first - q.first) * (p.first - q.first);
}
// returns a value proportional to the distance
// between the point p and the line joining the
// points p1 and p2
int lineDist(iPair p1, iPair p2, iPair p)
{
return abs ((p.second - p1.second) * (p2.first - p1.first) -
(p2.second - p1.second) * (p.first - p1.first));
}
// End points of line L are p1 and p2. side can have value
// 1 or -1 specifying each of the parts made by the line L
void quickHull(iPair a[], int n, iPair p1, iPair p2, int side)
{
int ind = -1;
int max_dist = 0;
// finding the point with maximum distance
// from L and also on the specified side of L.
for (int i = 0; i < n; i++)
{
int temp = lineDist(p1, p2, a[i]);
if (findSide(p1, p2, a[i]) == side && temp > max_dist)
{
ind = i;
max_dist = temp;
}
}
// If no point is found, add the end points
// of L to the convex hull.
if (ind == -1)
{
hull.insert(p1);
hull.insert(p2);
return;
}
// Recur for the two parts divided by a[ind]
quickHull(a, n, a[ind], p1, -findSide(a[ind], p1, p2));
quickHull(a, n, a[ind], p2, -findSide(a[ind], p2, p1));
}
void printHull(iPair a[], int n)
{
// a[i].second -> y-coordinate of the ith point
if (n < 3)
{
cout << "Convex hull not possible\n";
return;
}
// Finding the point with minimum and
// maximum x-coordinate
int min_x = 0, max_x = 0;
for (int i = 1; i < n; i++)
{
if (a[i].first < a[min_x].first)
min_x = i;
if (a[i].first > a[max_x].first)
max_x = i;
}
// Recursively find convex hull points on
// one side of line joining a[min_x] and
// a[max_x].
quickHull(a, n, a[min_x], a[max_x], 1);
// Recursively find convex hull points on
// other side of line joining a[min_x] and
// a[max_x]
quickHull(a, n, a[min_x], a[max_x], -1);
cout << "The points in Convex Hull are:\n";
while (!hull.empty())
{
cout << "(" << ( *hull.begin()).first << ", "
<< (*hull.begin()).second << ") ";
hull.erase(hull.begin());
}
}
// Driver code
int main()
{
iPair a[] = {{0, 3}, {1, 1}, {2, 2}, {4, 4},
{0, 0}, {1, 2}, {3, 1}, {3, 3}};
int n = sizeof(a) / sizeof(a[0]);
printHull(a, n);
return 0;
}
|
code/computational_geometry/src/quick_hull/test_data.csv | x,y
0.321534855,0.036295831
0.024023581,-0.23567288
0.045908512,-0.415640992
0.3218384,0.13798507
0.115064798,-0.105952147
0.262254,-0.297028733
-0.161920957,-0.405533972
0.190537863,0.369860101
0.238709092,-0.016298271
0.074958887,-0.165982511
0.331934184,-0.18218141
0.077036358,-0.249943064
0.2069243,-0.223297076
0.046040795,-0.192357319
0.050542958,0.475492946
-0.390058917,0.279782952
0.312069339,-0.050632987
0.011388127,0.40025047
0.00964515,0.10602511
-0.035979332,0.295363946
0.181829087,0.001454398
0.444056063,0.250249717
-0.053017525,-0.065539216
0.482389623,-0.477617
-0.308922685,-0.063561122
-0.271780741,0.18108106
0.429362652,0.298089796
-0.004796652,0.382663813
0.430695573,-0.29950735
0.179966839,-0.297346747
0.493216685,0.492809416
-0.352148791,0.43526562
-0.490736801,0.186582687
-0.104792472,-0.247073392
0.437496186,-0.00160628
0.003256208,-0.272919432
0.043103782,0.445260405
0.491619838,-0.345391701
0.001675087,0.153183767
-0.440428957,-0.289485599 |
code/computational_geometry/src/quick_hull/test_data_soln.txt | -0.161920957418085 -0.4055339716426413
0.05054295812784038 0.4754929463150845
0.4823896228171788 -0.4776170002088109
0.4932166845474547 0.4928094162538735
-0.3521487911717489 0.4352656197131292
-0.4907368011686362 0.1865826865533206
0.4916198379282093 -0.345391701297268
-0.4404289572876217 -0.2894855991839297
|
code/computational_geometry/src/sphere_tetrahedron_intersection/luvector.hpp | /*
* N dimensional loop unrolled vector class.
*
* https://github.com/RedBlight/LoopUnrolledVector
*
* Refactored a little bit for "cosmos" repository.
*
*/
#ifndef LU_VECTOR_INCLUDED
#define LU_VECTOR_INCLUDED
#include <sstream>
#include <string>
#include <complex>
#include <vector>
#include <iostream>
namespace LUV
{
// LuVector.hpp
template<std::size_t N, class T>
class LuVector;
template<class T>
using LuVector2 = LuVector<2, T>;
template<class T>
using LuVector3 = LuVector<3, T>;
using LuVector2f = LuVector<2, float>;
using LuVector2d = LuVector<2, double>;
using LuVector2c = LuVector<2, std::complex<double>>;
using LuVector3f = LuVector<3, float>;
using LuVector3d = LuVector<3, double>;
using LuVector3c = LuVector<3, std::complex<double>>;
// Added for cosmos
const double pi = 3.14159265358979323846;
// LuVector_Op.hpp
template<std::size_t N>
struct LoopIndex
{
};
template<class T, class S>
struct OpCopy
{
inline void operator ()(T& lhs, const S& rhs)
{
lhs = rhs;
}
};
//////////////////////////////////////////////////////////////
template<class T, class S>
struct OpAdd
{
inline void operator ()(T& lhs, const S& rhs)
{
lhs += rhs;
}
};
template<class T, class S>
struct OpSub
{
inline void operator ()(T& lhs, const S& rhs)
{
lhs -= rhs;
}
};
template<class T, class S>
struct OpMul
{
inline void operator ()(T& lhs, const S& rhs)
{
lhs *= rhs;
}
};
template<class T, class S>
struct OpDiv
{
inline void operator ()(T& lhs, const S& rhs)
{
lhs /= rhs;
}
};
//////////////////////////////////////////////////////////////
template<class T, class S>
struct OpAbs
{
inline void operator ()(T& lhs, const S& rhs)
{
lhs = std::abs(rhs);
}
};
template<class T, class S>
struct OpArg
{
inline void operator ()(T& lhs, const S& rhs)
{
lhs = std::arg(rhs);
}
};
template<std::size_t N, class T, class S>
struct OpMin
{
inline void operator ()(LuVector<N, T>& result, const LuVector<N, T>& lhs, const LuVector<N, S>& rhs, const std::size_t& I)
{
result[I] = lhs[I] < rhs[I] ? lhs[I] : rhs[I];
}
};
template<std::size_t N, class T, class S>
struct OpMax
{
inline void operator ()(LuVector<N, T>& result, const LuVector<N, T>& lhs, const LuVector<N, S>& rhs, const std::size_t& I)
{
result[I] = lhs[I] > rhs[I] ? lhs[I] : rhs[I];
}
};
template<std::size_t N, class T, class S>
struct OpDot
{
inline void operator ()(T& result, const LuVector<N, T>& lhs, const LuVector<N, S>& rhs, const std::size_t& I)
{
result += lhs[I] * rhs[I];
}
};
//////////////////////////////////////////////////////////////
template<class T>
struct OpOstream
{
inline void operator ()(std::ostream& lhs, const T& rhs, const std::string& delimiter)
{
lhs << rhs << delimiter;
}
};
// LuVector_Unroll.hpp
// VECTOR OP SCALAR
template<std::size_t I, std::size_t N, class T, class S, template<class, class> class OP>
inline void Unroll(LuVector<N, T>& lhs, const S& rhs, OP<T, S> operation, LoopIndex<I>)
{
Unroll(lhs, rhs, operation, LoopIndex<I-1>());
operation(lhs[I], rhs);
}
template<std::size_t N, class T, class S, template<class, class> class OP>
inline void Unroll(LuVector<N, T>& lhs, const S& rhs, OP<T, S> operation, LoopIndex<0>)
{
operation(lhs[0], rhs);
}
// SCALAR OP VECTOR
template<std::size_t I, std::size_t N, class T, class S, template<class, class> class OP>
inline void Unroll(S& lhs, const LuVector<N, T>& rhs, OP<T, S> operation, LoopIndex<I>)
{
Unroll(lhs, rhs, operation, LoopIndex<I-1>());
operation(lhs, rhs[I]);
}
template<std::size_t N, class T, class S, template<class, class> class OP>
inline void Unroll(S& lhs, const LuVector<N, T>& rhs, OP<T, S> operation, LoopIndex<0>)
{
operation(lhs, rhs[0]);
}
// VECTOR OP VECTOR
template<std::size_t I, std::size_t N, class T, class S, template<class, class> class OP>
inline void Unroll(LuVector<N, T>& lhs, const LuVector<N, S>& rhs, OP<T, S> operation, LoopIndex<I>)
{
Unroll(lhs, rhs, operation, LoopIndex<I-1>());
operation(lhs[I], rhs[I]);
}
template<std::size_t N, class T, class S, template<class, class> class OP>
inline void Unroll(LuVector<N, T>& lhs, const LuVector<N, S>& rhs, OP<T, S> operation, LoopIndex<0>)
{
operation(lhs[0], rhs[0]);
}
// SCALAR = VECTOR OP VECTOR (could be cross-element)
template<std::size_t I, std::size_t N, class T, class S, template<std::size_t, class, class> class OP>
inline void Unroll(T& result, const LuVector<N, T>& lhs, const LuVector<N, S>& rhs, OP<N, T, S> operation, LoopIndex<I>)
{
Unroll(result, lhs, rhs, operation, LoopIndex<I-1>());
operation(result, lhs, rhs, I);
}
template<std::size_t N, class T, class S, template<std::size_t, class, class> class OP>
inline void Unroll(T& result, const LuVector<N, T>& lhs, const LuVector<N, S>& rhs, OP<N, T, S> operation, LoopIndex<0>)
{
operation(result, lhs, rhs, 0);
}
// VECTOR = VECTOR OP VECTOR (could be cross-element)
template<std::size_t I, std::size_t N, class T, class S, template<std::size_t, class, class> class OP>
inline void Unroll(LuVector<N, T>& result, const LuVector<N, T>& lhs, const LuVector<N, S>& rhs, OP<N, T, S> operation, LoopIndex<I>)
{
Unroll(result, lhs, rhs, operation, LoopIndex<I-1>());
operation(result, lhs, rhs, I);
}
template<std::size_t N, class T, class S, template<std::size_t, class, class> class OP>
inline void Unroll(LuVector<N, T>& result, const LuVector<N, T>& lhs, const LuVector<N, S>& rhs, OP<N, T, S> operation, LoopIndex<0>)
{
operation(result, lhs, rhs, 0);
}
// OSTREAM OP VECTOR
template<std::size_t I, std::size_t N, class T, template<class> class OP>
inline void Unroll(std::ostream& lhs, const LuVector<N, T>& rhs, const std::string& delimiter, OP<T> operation, LoopIndex<I>)
{
Unroll(lhs, rhs, delimiter, operation, LoopIndex<I-1>());
operation(lhs, rhs[I], delimiter);
}
template<std::size_t N, class T, template<class> class OP>
inline void Unroll(std::ostream& lhs, const LuVector<N, T>& rhs, const std::string& delimiter, OP<T> operation, LoopIndex<0>)
{
operation(lhs, rhs[0], delimiter);
}
// LuVector_Body.hpp
template<std::size_t N, class T>
class LuVector
{
public:
LuVector() = default;
~LuVector() = default;
template<class... S>
LuVector(const S&... elem) : _{ static_cast<T>(elem) ...}
{
}
LuVector(const LuVector<N, const T>& other) : _{ other._ }
{
}
template<class S>
LuVector(const LuVector<N, S>& other)
{
Unroll(*this, other, OpCopy<T, S>(), LoopIndex<N-1>());
}
template<class S>
LuVector(const S& scalar)
{
Unroll(*this, scalar, OpCopy<T, S>(), LoopIndex<N-1>());
}
template<class S>
inline LuVector<N, T>& operator =(const LuVector<N, S>& other)
{
Unroll(*this, other, OpCopy<T, S>(), LoopIndex<N-1>());
return *this;
}
inline const T& operator [](const std::size_t& idx) const
{
return _[idx];
}
inline T& operator [](const std::size_t& idx)
{
return _[idx];
}
inline std::string ToString() const
{
std::stringstream ss;
ss << "(";
Unroll(ss, *this, ",", OpOstream<T>(), LoopIndex<N-2>());
ss << _[N-1] << ")";
return std::string(ss.str());
}
private:
T _[N];
};
// LuVector_Overload.hpp
// OSTREAM << VECTOR
template<std::size_t N, class T>
std::ostream& operator <<(std::ostream& lhs, const LuVector<N, T>& rhs)
{
lhs << "(";
Unroll(lhs, rhs, ",", OpOstream<T>(), LoopIndex<N-2>());
lhs << rhs[N-1] << ")";
return lhs;
}
// VECTOR += SCALAR
template<std::size_t N, class T, class S>
inline LuVector<N, T>& operator +=(LuVector<N, T>& lhs, const S& rhs)
{
Unroll(lhs, rhs, OpAdd<T, S>(), LoopIndex<N-1>());
return lhs;
}
// VECTOR -= SCALAR
template<std::size_t N, class T, class S>
inline LuVector<N, T>& operator -=(LuVector<N, T>& lhs, const S& rhs)
{
Unroll(lhs, rhs, OpSub<T, S>(), LoopIndex<N-1>());
return lhs;
}
// VECTOR *= SCALAR
template<std::size_t N, class T, class S>
inline LuVector<N, T>& operator *=(LuVector<N, T>& lhs, const S& rhs)
{
Unroll(lhs, rhs, OpMul<T, S>(), LoopIndex<N-1>());
return lhs;
}
// VECTOR /= SCALAR
template<std::size_t N, class T, class S>
inline LuVector<N, T>& operator /=(LuVector<N, T>& lhs, const S& rhs)
{
Unroll(lhs, rhs, OpDiv<T, S>(), LoopIndex<N-1>());
return lhs;
}
//////////////////////////////////////////////////////////////
// VECTOR += VECTOR
template<std::size_t N, class T, class S>
inline LuVector<N, T>& operator +=(LuVector<N, T>& lhs, const LuVector<N, S>& rhs)
{
Unroll(lhs, rhs, OpAdd<T, S>(), LoopIndex<N-1>());
return lhs;
}
// VECTOR -= VECTOR
template<std::size_t N, class T, class S>
inline LuVector<N, T>& operator -=(LuVector<N, T>& lhs, const LuVector<N, S>& rhs)
{
Unroll(lhs, rhs, OpSub<T, S>(), LoopIndex<N-1>());
return lhs;
}
// VECTOR *= VECTOR
template<std::size_t N, class T, class S>
inline LuVector<N, T>& operator *=(LuVector<N, T>& lhs, const LuVector<N, S>& rhs)
{
Unroll(lhs, rhs, OpMul<T, S>(), LoopIndex<N-1>());
return lhs;
}
// VECTOR /= VECTOR
template<std::size_t N, class T, class S>
inline LuVector<N, T>& operator /=(LuVector<N, T>& lhs, const LuVector<N, S>& rhs)
{
Unroll(lhs, rhs, OpDiv<T, S>(), LoopIndex<N-1>());
return lhs;
}
//////////////////////////////////////////////////////////////
// VECTOR + SCALAR
template<std::size_t N, class T, class S>
inline LuVector<N, T> operator +(const LuVector<N, T>& lhs, const S& rhs)
{
LuVector<N, T> result(lhs);
return result += rhs;
}
// SCALAR + VECTOR
template<std::size_t N, class T, class S>
inline LuVector<N, T> operator +(const T& lhs, const LuVector<N, S>& rhs)
{
LuVector<N, T> result(lhs);
return result += rhs;
}
// VECTOR - SCALAR
template<std::size_t N, class T, class S>
inline LuVector<N, T> operator -(const LuVector<N, T>& lhs, const S& rhs)
{
LuVector<N, T> result(lhs);
return result -= rhs;
}
// SCALAR - VECTOR
template<std::size_t N, class T, class S>
inline LuVector<N, T> operator -(const T& lhs, const LuVector<N, S>& rhs)
{
LuVector<N, T> result(lhs);
return result -= rhs;
}
// VECTOR * SCALAR
template<std::size_t N, class T, class S>
inline LuVector<N, T> operator *(const LuVector<N, T>& lhs, const S& rhs)
{
LuVector<N, T> result(lhs);
return result *= rhs;
}
// SCALAR * VECTOR
template<std::size_t N, class T, class S>
inline LuVector<N, T> operator *(const T& lhs, const LuVector<N, S>& rhs)
{
LuVector<N, T> result(lhs);
return result *= rhs;
}
// VECTOR / SCALAR
template<std::size_t N, class T, class S>
inline LuVector<N, T> operator /(const LuVector<N, T>& lhs, const S& rhs)
{
LuVector<N, T> result(lhs);
return result /= rhs;
}
// SCALAR / VECTOR
template<std::size_t N, class T, class S>
inline LuVector<N, T> operator /(const T& lhs, const LuVector<N, S>& rhs)
{
LuVector<N, T> result(lhs);
return result /= rhs;
}
//////////////////////////////////////////////////////////////
// VECTOR + VECTOR
template<std::size_t N, class T, class S>
inline LuVector<N, T> operator +(const LuVector<N, T>& lhs, const LuVector<N, S>& rhs)
{
LuVector<N, T> result(lhs);
return result += rhs;
}
// VECTOR - VECTOR
template<std::size_t N, class T, class S>
inline LuVector<N, T> operator -(const LuVector<N, T>& lhs, const LuVector<N, S>& rhs)
{
LuVector<N, T> result(lhs);
return result -= rhs;
}
// VECTOR * VECTOR
template<std::size_t N, class T, class S>
inline LuVector<N, T> operator *(const LuVector<N, T>& lhs, const LuVector<N, S>& rhs)
{
LuVector<N, T> result(lhs);
return result *= rhs;
}
// VECTOR / VECTOR
template<std::size_t N, class T, class S>
inline LuVector<N, T> operator /(const LuVector<N, T>& lhs, const LuVector<N, S>& rhs)
{
LuVector<N, T> result(lhs);
return result /= rhs;
}
//////////////////////////////////////////////////////////////
// - VECTOR
template<std::size_t N, class T>
inline LuVector<N, T> operator -(const LuVector<N, T>& vec)
{
return T(0) - vec;
}
//////////////////////////////////////////////////////////////
// LuVector_Math.hpp
template<std::size_t N, class T>
inline T Sum(const LuVector<N, T>& vec)
{
T result = 0;
Unroll(result, vec, OpAdd<T, T>(), LoopIndex<N-1>());
return result;
}
// Abs
template<std::size_t N, class T>
inline LuVector<N, T> Abs(const LuVector<N, T>& vec)
{
LuVector<N, T> absVec;
Unroll(absVec, vec, OpAbs<T, T>(), LoopIndex<N-1>());
return absVec;
}
// Length
template<std::size_t N, class T>
inline T Length(const LuVector<N, T>& vec)
{
T result = 0;
Unroll(result, vec, vec, OpDot<N, T, T>(), LoopIndex<N-1>());
return sqrt(result);
}
// Unit
template<std::size_t N, class T>
inline LuVector<N, T> Unit(const LuVector<N, T>& vec)
{
return vec / Length(vec);
}
//////////////////////////////////////////////////////////////
// Abs Complex
template<std::size_t N, class T>
inline LuVector<N, T> Abs(const LuVector<N, std::complex<T>>& vec)
{
LuVector<N, T> absVec;
Unroll(absVec, vec, OpAbs<T, std::complex<T>>(), LoopIndex<N-1>());
return absVec;
}
// Arg Complex
template<std::size_t N, class T>
inline LuVector<N, T> Arg(const LuVector<N, std::complex<T>>& vec)
{
LuVector<N, T> argVec;
Unroll(argVec, vec, OpArg<T, std::complex<T>>(), LoopIndex<N-1>());
return argVec;
}
// Length Complex
template<std::size_t N, class T>
inline T Length(const LuVector<N, std::complex<T>>& vec)
{
return Length(Abs(vec));
}
// Unit Complex
template<std::size_t N, class T>
inline LuVector<N, std::complex<T>> Unit(const LuVector<N, std::complex<T>>& vec)
{
return vec / Length(vec);
}
//////////////////////////////////////////////////////////////
// Min
template<std::size_t N, class T, class S>
inline LuVector<N, T> Min(const LuVector<N, T>& lhs, const LuVector<N, S>& rhs)
{
LuVector<N, T> result;
Unroll(result, lhs, rhs, OpMin<N, T, S>(), LoopIndex<N-1>());
return result;
}
// Max
template<std::size_t N, class T, class S>
inline LuVector<N, T> Max(const LuVector<N, T>& lhs, const LuVector<N, S>& rhs)
{
LuVector<N, T> result;
Unroll(result, lhs, rhs, OpMax<N, T, S>(), LoopIndex<N-1>());
return result;
}
// Dot
template<std::size_t N, class T, class S>
inline T Dot(const LuVector<N, T>& lhs, const LuVector<N, S>& rhs)
{
T result = 0;
Unroll(result, lhs, rhs, OpDot<N, T, S>(), LoopIndex<N-1>());
return result;
}
// Cross
template<class T, class S>
inline LuVector<3, T> Cross(const LuVector<3, T>& lhs, const LuVector<3, S>& rhs)
{
return LuVector<3, T>(
lhs[1] * rhs[2] - lhs[2] * rhs[1],
lhs[2] * rhs[0] - lhs[0] * rhs[2],
lhs[0] * rhs[1] - lhs[1] * rhs[0]
);
}
//////////////////////////////////////////////////////////////
// Reflect
template<std::size_t N, class T, class S>
inline LuVector<N, T> Reflect(const LuVector<N, T>& vec, const LuVector<N, S>& normal)
{
return vec - normal * Dot(vec, normal) * 2;
}
// Rotate...
//////////////////////////////////////////////////////////////
// CtsToSph
template<class T>
inline LuVector<3, T> CtsToSph(const LuVector<3, T>& cts)
{
T len = Length(cts);
return LuVector<3, T>(
len,
cts[0] == 0 && cts[1] == 0 ? 0 : std::atan2(cts[1], cts[0]),
std::acos(cts[2] / len)
);
}
// SphToCts
template<class T>
inline LuVector<3, T> SphToCts(const LuVector<3, T>& sph)
{
T planarVal = sph[0] * std::sin(sph[2]);
return LuVector<3, T>(
planarVal * std::cos(sph[1]),
planarVal * std::sin(sph[1]),
sph[0] * std::cos(sph[2])
);
}
// CtsToPol
template<class T>
inline LuVector<2, T> CtsToPol(const LuVector<2, T>& cts)
{
T len = Length(cts);
return LuVector<2, T>(
len,
cts[0] == 0 && cts[1] == 0 ? 0 : std::atan2(cts[1], cts[0])
);
}
// PolToCts
template<class T>
inline LuVector<2, T> PolToCts(const LuVector<2, T>& pol)
{
return LuVector<2, T>(
pol[0] * std::cos(pol[1]),
pol[0] * std::sin(pol[1])
);
}
//////////////////////////////////////////////////////////////
// OrthonormalSet N=3
// N: looking outside the sphere at given angles
// U: up vector
// R: right vector, parallel to XY plane
// N = U X R
template<class T>
inline void OrthonormalSet(const T& angP, const T& angT, LuVector<3, T>& dirN, LuVector<3, T>& dirU, LuVector<3, T>& dirR)
{
T cp = std::cos(angP);
T sp = std::sin(angP);
T ct = std::cos(angT);
T st = std::sin(angT);
dirN[0] = st * cp;
dirN[1] = st * sp;
dirN[2] = ct;
dirR[0] = sp;
dirR[1] = -cp;
dirR[2] = 0;
dirU = Cross(dirR, dirN);
}
// OrthonormalSet N=2
template<class T>
inline void OrthonormalSet(const T& ang, LuVector<2, T>& dirN, LuVector<2, T>& dirR)
{
T c = std::cos(ang);
T s = std::sin(ang);
dirN[0] = c;
dirN[1] = s;
dirR[0] = s;
dirR[1] = -c;
}
// OrthogonalR N=3
template<class T>
inline LuVector<3, T> OrthonormalR(const LuVector<3, T>& dirN)
{
T ang = dirN[0] == 0 && dirN[1] == 0 ? 0 : std::atan2(dirN[1], dirN[0]);
T c = std::cos(ang);
T s = std::sin(ang);
return LuVector<3, T>(s, -c, 0);
}
// OrthogonalR N=2
template<class T>
inline LuVector<2, T> OrthonormalR(const LuVector<2, T>& dirN)
{
return LuVector<2, T>(dirN[1], -dirN[0]);
}
// OrthogonalU N=3
template<class T>
inline LuVector<3, T> OrthonormalU(const LuVector<3, T>& dirN)
{
return Cross(OrthogonalR(dirN), dirN);
}
// LuVector_Geometry.hpp
// ProjLine N=3
template<class T>
inline LuVector<3, T> ProjLine(const LuVector<3, T>& vec, const LuVector<3, T>&v1, const LuVector<3, T>& v2)
{
LuVector<3, T> v12 = Unit(v2 - v1);
return v1 + Dot(v12, vec - v1) * v12;
}
// ProjLine N=2
template<class T>
inline LuVector<2, T> ProjLine(const LuVector<2, T>& vec, const LuVector<2, T>&v1, const LuVector<2, T>& v2)
{
LuVector<2, T> v12 = Unit(v2 - v1);
return v1 + Dot(v12, vec - v1) * v12;
}
// ProjLineL N=3
template<class T>
inline LuVector<3, T> ProjLineL(const LuVector<3, T>& vec, const LuVector<3, T>&v1, const LuVector<3, T>& lineDir)
{
return v1 + Dot(lineDir, vec - v1) * lineDir;
}
// ProjLineL N=2
template<class T>
inline LuVector<2, T> ProjLineL(const LuVector<2, T>& vec, const LuVector<2, T>&v1, const LuVector<2, T>& lineDir)
{
return v1 + Dot(lineDir, vec - v1) * lineDir;
}
// LineNormal N=3
template<class T>
inline LuVector<3, T> LineNormal(const LuVector<3, T>& v1, const LuVector<3, T>& v2)
{
LuVector<3, T> v12 = Unit(v2 - v1);
return OrthogonalR(v12);
}
// LineNormal N=2
template<class T>
inline LuVector<2, T> LineNormal(const LuVector<2, T>& v1, const LuVector<2, T>& v2)
{
LuVector<2, T> v12 = Unit(v2 - v1);
return OrthogonalR(v12);
}
// LineNormalL N=3
template<class T>
inline LuVector<3, T> LineNormalL(const LuVector<3, T>& lineDir)
{
return OrthogonalR(lineDir);
}
// LineNormalL N=2
template<class T>
inline LuVector<2, T> LineNormalL(const LuVector<2, T>& lineDir)
{
return OrthogonalR(lineDir);
}
// LineNormalP N=3
template<class T>
inline LuVector<3, T> LineNormalP(const LuVector<3, T>& vec, const LuVector<3, T>& v1, const LuVector<3, T>& v2)
{
LuVector<3, T> v12 = Unit(v2 - v1);
LuVector<3, T> ort = vec - ProjLineL(vec, v1, v12);
T len = Length(ort);
return len > 0 ? ort / len : LineNormalL(v12);
}
// LineNormalP N=2
template<class T>
inline LuVector<2, T> LineNormalP(const LuVector<2, T>& vec, const LuVector<2, T>& v1, const LuVector<2, T>& v2)
{
LuVector<2, T> v12 = Unit(v2 - v1);
LuVector<2, T> ort = vec - ProjLineL(vec, v1, v12);
T len = Length(ort);
return len > 0 ? ort / len : LineNormalL(v12);
}
// LineNormalPL N=3
template<class T>
inline LuVector<3, T> LineNormalPL(const LuVector<3, T>& vec, const LuVector<3, T>& v1, const LuVector<3, T>& lineDir)
{
LuVector<3, T> ort = vec - ProjLineL(vec, v1, lineDir);
T len = Length(ort);
return len > 0 ? ort / len : LineNormalL(lineDir);
}
// LineNormalPL N=2
template<class T>
inline LuVector<2, T> LineNormalPL(const LuVector<2, T>& vec, const LuVector<2, T>& v1, const LuVector<2, T>& lineDir)
{
LuVector<2, T> ort = vec - ProjLineL(vec, v1, lineDir);
T len = Length(ort);
return len > 0 ? ort / len : LineNormalL(lineDir);
}
//////////////////////////////////////////////////////////////
// ProjPlane
template<class T>
inline LuVector<3, T> ProjPlane(const LuVector<3, T>& vec, const LuVector<3, T>& v1, const LuVector<3, T>& n)
{
return vec - Dot(vec - v1, n) * n;
}
// PlaneNormal
template<class T>
inline LuVector<3, T> PlaneNormal(const LuVector<3, T>& v1, const LuVector<3, T>& v2, const LuVector<3, T>& v3)
{
return Unit(Cross(v2 - v1, v3 - v1));
}
// PlaneNormalP
template<class T>
inline LuVector<3, T> PlaneNormalP( const LuVector<3, T>& vec, const LuVector<3, T>& v1, const LuVector<3, T>& v2, const LuVector<3, T>& v3)
{
LuVector<3, T> n = PlaneNormal(v1, v2, v3);
return Dot(n, vec - v1) > 0 ? n : -n;
}
// PlaneNormalPN
template<class T>
inline LuVector<3, T> PlaneNormalPN( const LuVector<3, T>& vec, const LuVector<3, T>& v1, const LuVector<3, T>& n)
{
return Dot(n, vec - v1)> 0 ? n : -n;
}
};
#endif |
code/computational_geometry/src/sphere_tetrahedron_intersection/sphere_tetrahedron_intersection.cpp | /*
* Analytical calculations for sphere-tetrahedron intersections.
*
* See here for it's mathematical description:
* https://www.quora.com/What-are-some-equations-that-you-made-up/answer/Mahmut-Akku%C5%9F
*
* - RedBlight
*
*/
#include <cmath>
#include "LuVector.hpp"
using Vec3 = LUV::LuVector<3, double>;
// Returns the solid angle of sphere cap contended by a cone.
// Apex of the cone is center of the sphere.
double SolidAngleCap(double apexAngle)
{
return 2.0 * LUV::pi * (1.0 - std::cos(apexAngle));
}
// Returns the solid angle of a spherical triangle.
// v1, v2, v3 are vertices of the triangle residing on a unit sphere.
double SolidAngleSphtri(const Vec3& v1, const Vec3& v2, const Vec3& v3)
{
double ang0 = std::acos(LUV::Dot(v1, v2));
double ang1 = std::acos(LUV::Dot(v2, v3));
double ang2 = std::acos(LUV::Dot(v3, v1));
double angSum = (ang0 + ang1 + ang2) / 2.0;
return 4.0 * std::atan(std::sqrt(
std::tan(angSum / 2.0) *
std::tan((angSum - ang0) / 2.0) *
std::tan((angSum - ang1) / 2.0) *
std::tan((angSum - ang2) / 2.0)
));
}
// Returns the volume of spherical cap.
double VolumeCap(double radius, double height)
{
return radius * radius * height * LUV::pi * (2.0 / 3.0);
}
// Returns the volume of cone.
double VolumeCone(double radius, double height)
{
return radius * radius * height * LUV::pi * (1.0 / 3.0);
}
// Returns the volume of tetrahedron given it's 4 vertices.
double VolumeTetrahedron(const Vec3& v1, const Vec3& v2, const Vec3& v3, const Vec3& v4)
{
return std::abs(LUV::Dot(v1 - v4, LUV::Cross(v2 - v4, v3 - v4))) / 6.0;
}
// Returns the volume of triangular slice taken from a sphere.
double VolumeSphtri(const Vec3& v1, const Vec3& v2, const Vec3& v3, double radius)
{
return SolidAngleSphtri(v1, v2, v3) * radius * radius * radius / 3.0;
}
/*
* Observation tetrahedra (OT) are special tetrahedra constructed for analytical calculations.
* OTs have right angles in many of their corners, and one of their vertices are the center of the sphere.
* For this reason, their intersections with the sphere can be calculated analytically.
* When 24 OTs contructed for each vertex, of each edge, of each face, of any arbitrary tetrahedron,
* their combinations can be used to analytically calculate intersections of any arbitrary sphere and tetrahedron.
*
*/
class ObservationTetrahedron
{
public:
// Cartesian coordinates of vertices:
Vec3 posR, posA, posB, posC;
// Distances from posR:
double lenA, lenB, lenC;
// Direction of sphere-edge intersection points as radius increases:
Vec3 prdA, prdB, prdC, prdD, prdE, prdF;
// Some angles between lines:
double angBAC, angERA, angFAE;
// Max. solid angle contended by OT
double solidAngleFull;
// Constructor
ObservationTetrahedron(const Vec3& vR, const Vec3& vA, const Vec3& vB, const Vec3& vC)
{
posR = vR;
posA = vA;
posB = vB;
posC = vC;
Vec3 AmR = vA - vR;
Vec3 BmR = vB - vR;
Vec3 CmR = vC - vR;
Vec3 BmA = vB - vA;
Vec3 CmA = vC - vA;
Vec3 CmB = vC - vB;
lenA = LUV::Length(AmR);
lenB = LUV::Length(BmR);
lenC = LUV::Length(CmR);
prdA = AmR / lenA;
prdB = BmR / lenB;
prdC = CmR / lenC;
prdD = BmA / LUV::Length(BmA);
prdE = CmA / LUV::Length(CmA);
prdF = CmB / LUV::Length(CmB);
angBAC = std::acos(LUV::Dot(prdD, prdE));
solidAngleFull = SolidAngleSphtri(prdA, prdB, prdC);
}
// Solid angle of the sphere subtended by OT as a function of sphere radius.
double GetSolidAngle(double radius)
{
RecalculateForRadius(radius);
if (radius >= lenC)
return 0;
else if (radius >= lenB)
return SolidAngleSphtri(dirA, dirC, dirF) -
SolidAngleCap(angERA) * angFAE / (2.0 * LUV::pi);
else if (radius >= lenA)
return solidAngleFull -
SolidAngleCap(angERA) * angBAC / (2.0 * LUV::pi);
return solidAngleFull;
}
// Surface area of the sphere subtended by OT as a function of sphere radius.
double GetSurfaceArea(double radius)
{
return GetSolidAngle(radius) * radius * radius;
}
// Volume of OT-sphere intersection, as a function of sphere radius.
double GetVolume(double radius)
{
RecalculateForRadius(radius);
if (radius >= lenC)
return VolumeTetrahedron(posR, posA, posB, posC);
else if (radius >= lenB)
return VolumeSphtri(dirA, dirC, dirF, radius) - (
VolumeCap(radius, LUV::Length(prpA - posA)) -
VolumeCone(prlE, lenA)
) * angFAE / (2.0 * LUV::pi) +
VolumeTetrahedron(posR, posA, posB, prpF);
else if (radius >= lenA)
return VolumeSphtri(dirA, dirB, dirC, radius) - (
VolumeCap(radius, LUV::Length(prpA - posA)) -
VolumeCone(prlE, lenA)
) * angBAC / (2.0 * LUV::pi);
return VolumeSphtri(dirA, dirB, dirC, radius);
}
private:
// Angles of RBF triangle
double angRBF, angBFR, angFRB;
// Distance of sphere-edge intersections:
double prlA, prlB, prlC, prlD, prlE, prlF;
//R->A, R->B, R->C, A->B, A->C, B->C
// Positions of sphere-edge intersections:
Vec3 prpA, prpB, prpC, prpD, prpE, prpF;
// Positions relative to posR:
// All have the length = radius
Vec3 vecA, vecB, vecC, vecD, vecE, vecF;
// Directions from posR:
Vec3 dirA, dirB, dirC, dirD, dirE, dirF;
// OT vertices are not actually dependent on the radius of the sphere, only the center.
// But some values need to be calculated for each radius.
void RecalculateForRadius(double radius)
{
angRBF = std::acos(LUV::Dot(posR - posB, posC - posB));
angBFR = std::asin(lenB * std::sin(angRBF) / radius);
angFRB = LUV::pi - (angRBF + angBFR);
prlA = radius;
prlB = radius;
prlC = radius;
prlD = std::sqrt(radius * radius - lenA * lenA);
prlE = prlD;
prlF = lenB * std::sin(angFRB) / sin(angBFR);
prpA = posR + prdA * prlA;
prpB = posR + prdB * prlB;
prpC = posR + prdC * prlC;
prpD = posA + prdD * prlD;
prpE = posA + prdE * prlE;
prpF = posB + prdF * prlF;
vecA = prpA - posR;
vecB = prpB - posR;
vecC = prpC - posR;
vecD = prpD - posR;
vecE = prpE - posR;
vecF = prpF - posR;
dirA = vecA / LUV::Length(vecA);
dirB = vecB / LUV::Length(vecB);
dirC = vecC / LUV::Length(vecC);
dirD = vecD / LUV::Length(vecD);
dirE = vecE / LUV::Length(vecE);
dirF = vecF / LUV::Length(vecF);
angERA = std::acos(LUV::Dot(dirE, dirA));
Vec3 vecAF = prpF - posA;
Vec3 vecAE = prpE - posA;
angFAE = std::acos(LUV::Dot(vecAF, vecAE) / (LUV::Length(vecAF) * LUV::Length(vecAE)));
}
};
// Main class for the intersection.
class SphereTetrahedronIntersection
{
public:
// Constructor,
// vecTetA..D are vertices of the tetrahedron.
// vecSphCenter is the center of the sphere.
SphereTetrahedronIntersection(const Vec3& vecTetA, const Vec3& vecTetB, const Vec3& vecTetC,
const Vec3& vecTetD, const Vec3& vecSphCenter)
{
// Adding OTs for each face of the tetrahedron.
AddOtForFace(vecTetA, vecTetB, vecTetC, vecTetD, vecSphCenter);
AddOtForFace(vecTetB, vecTetC, vecTetD, vecTetA, vecSphCenter);
AddOtForFace(vecTetC, vecTetD, vecTetA, vecTetB, vecSphCenter);
AddOtForFace(vecTetD, vecTetA, vecTetB, vecTetC, vecSphCenter);
// Calculating OT signs.
for (int idf = 0; idf < 4; ++idf)
for (int idl = 0; idl < 3; ++idl)
{
int ids = 3 * idf + idl;
int idp = 2 * ids;
int idm = idp + 1;
obsTetSgn.push_back(
LUV::Dot(obsTet[idp].prdA, dirN[idf]) *
LUV::Dot(obsTet[idp].prdF, dirL[ids]) *
LUV::Dot(obsTet[idp].prdD, dirU[ids])
);
obsTetSgn.push_back(
-1 *
LUV::Dot(obsTet[idm].prdA, dirN[idf]) *
LUV::Dot(obsTet[idm].prdF, dirL[ids]) *
LUV::Dot(obsTet[idm].prdD, dirU[ids])
);
}
}
// Solid angle subtended by tetrahedron, as a function of sphere radius.
double GetSolidAngle(double radius)
{
double solidAngle = 0;
for (int idx = 0; idx < 24; ++idx)
{
double solidAngleOt = obsTet[idx].GetSolidAngle(radius) * obsTetSgn[idx];
solidAngle += std::isnan(solidAngleOt) ? 0 : solidAngleOt;
}
return solidAngle;
}
// Surface area subtended by tetrahedron, as a function of sphere radius.
double GetSurfaceArea(double radius)
{
return GetSolidAngle(radius) * radius * radius;
}
// Sphere-tetrahedron intersection volume, as a function of sphere radius.
double GetVolume(double radius)
{
double volume = 0;
for (int idx = 0; idx < 24; ++idx)
{
double volumeOt = obsTet[idx].GetVolume(radius) * obsTetSgn[idx];
volume += std::isnan(volumeOt) ? 0 : volumeOt;
}
return volume;
}
private:
std::vector<ObservationTetrahedron> obsTet; //24 in total
std::vector<double> obsTetSgn;
std::vector<Vec3> dirN;
std::vector<Vec3> dirU;
std::vector<Vec3> dirL;
void AddOtForEdge(const Vec3& vecM, const Vec3& vecP, const Vec3& vecT, const Vec3& vecR)
{
Vec3 PmM = vecP - vecM;
dirL.push_back(PmM / LUV::Length(PmM));
Vec3 vecU = vecT - LUV::ProjLine(vecT, vecM, vecP);
dirU.push_back(vecU / LUV::Length(vecU));
Vec3 vecA = LUV::ProjPlane(vecR, vecM, LUV::PlaneNormal(vecM, vecP, vecT));
Vec3 vecB = LUV::ProjLine(vecA, vecM, vecP);
obsTet.push_back(ObservationTetrahedron(vecR, vecA, vecB, vecP));
obsTet.push_back(ObservationTetrahedron(vecR, vecA, vecB, vecM));
}
void AddOtForFace(const Vec3& vecA, const Vec3& vecB, const Vec3& vecC, const Vec3& vecU,
const Vec3& vecR)
{
Vec3 vecN = vecU - LUV::ProjPlane(vecU, vecA, LUV::PlaneNormal(vecA, vecB, vecC));
dirN.push_back(vecN / LUV::Length(vecN));
AddOtForEdge(vecA, vecB, vecC, vecR);
AddOtForEdge(vecB, vecC, vecA, vecR);
AddOtForEdge(vecC, vecA, vecB, vecR);
}
};
// An example usage...
int main()
{
// Tetrahedron with a volume of 1000
Vec3 vecTetA(0, 0, 0);
Vec3 vecTetB(10, 0, 0);
Vec3 vecTetC(0, 20, 0);
Vec3 vecTetD(0, 0, 30);
// Center of the sphere
Vec3 vecSphCenter(0, 0, 0);
// Intersection class
SphereTetrahedronIntersection testIntersection(vecTetA, vecTetB, vecTetC, vecTetD,
vecSphCenter);
// Demonstrating that numerical integral of surface area is equal to analytical calculation of volume:
int stepCount = 10000;
double radiusStart = 0;
double radiusEnd = 30;
double radiusDelta = (radiusEnd - radiusStart) / stepCount;
double volumeNumerical = 0;
for (double radius = radiusStart; radius < radiusEnd; radius += radiusDelta)
volumeNumerical += testIntersection.GetSurfaceArea(radius) * radiusDelta;
double volumeAnalytical = testIntersection.GetVolume(radiusEnd);
// These 2 values must be almost equal:
std::cout << volumeAnalytical << ", " << volumeNumerical << std::endl;
return 0;
}
|
code/computational_geometry/src/sutherland_hodgeman_clipping/README.md | ## Working of Sutherland Hodgeman Polygon Clipping
**Coordinates of rectangular clip window** :
xmin,ymin :`200 200`
xmax,ymax :`400 400`
**Polygon to be clipped** :
Number of sides :`3`
Enter the coordinates :
`150 300`
`300 150`
`300 300`
Before clipping:

After clipping:

---
<p align="center">
A massive collaborative effort by <a href="https://github.com/OpenGenus/cosmos">OpenGenus Foundation</a>
</p>
---
|
code/computational_geometry/src/sutherland_hodgeman_clipping/sutherland_hodgeman_clipping.c | #include<stdio.h>
#include<math.h>
#include<graphics.h>
#define round(a) ((int)(a+0.5))
// Part of Cosmos by OpenGenus Foundation
int k;
float xmin,ymin,xmax,ymax,arr[20],m;
void clipl(float x1,float y1,float x2,float y2) {
if(x2-x1)
m=(y2-y1)/(x2-x1);
else
m=100000;
if(x1 >= xmin && x2 >= xmin) {
arr[k]=x2;
arr[k+1]=y2;
k+=2;
}
if(x1 < xmin && x2 >= xmin) {
arr[k]=xmin;
arr[k+1]=y1+m*(xmin-x1);
arr[k+2]=x2;
arr[k+3]=y2;
k+=4;
}
if(x1 >= xmin && x2 < xmin) {
arr[k]=xmin;
arr[k+1]=y1+m*(xmin-x1);
k+=2;
}
}
void clipt(float x1,float y1,float x2,float y2) {
if(y2-y1)
m=(x2-x1)/(y2-y1);
else
m=100000;
if(y1 <= ymax && y2 <= ymax) {
arr[k]=x2;
arr[k+1]=y2;
k+=2;
}
if(y1 > ymax && y2 <= ymax) {
arr[k]=x1+m*(ymax-y1);
arr[k+1]=ymax;
arr[k+2]=x2;
arr[k+3]=y2;
k+=4;
}
if(y1 <= ymax && y2 > ymax) {
arr[k]=x1+m*(ymax-y1);
arr[k+1]=ymax;
k+=2;
}
}
void clipr(float x1,float y1,float x2,float y2) {
if(x2-x1)
m=(y2-y1)/(x2-x1);
else
m=100000;
if(x1 <= xmax && x2 <= xmax) {
arr[k]=x2;
arr[k+1]=y2;
k+=2;
}
if(x1 > xmax && x2 <= xmax) {
arr[k]=xmax;
arr[k+1]=y1+m*(xmax-x1);
arr[k+2]=x2;
arr[k+3]=y2;
k+=4;
}
if(x1 <= xmax && x2 > xmax) {
arr[k]=xmax;
arr[k+1]=y1+m*(xmax-x1);
k+=2;
}
}
void clipb(float x1,float y1,float x2,float y2) {
if(y2-y1)
m=(x2-x1)/(y2-y1);
else
m=100000;
if(y1 >= ymin && y2 >= ymin) {
arr[k]=x2;
arr[k+1]=y2;
k+=2;
}
if(y1 < ymin && y2 >= ymin) {
arr[k]=x1+m*(ymin-y1);
arr[k+1]=ymin;
arr[k+2]=x2;
arr[k+3]=y2;
k+=4;
}
if(y1 >= ymin && y2 < ymin) {
arr[k]=x1+m*(ymin-y1);
arr[k+1]=ymin;
k+=2;
}
}
void main() {
int gdriver=DETECT,gmode,n,poly[20],i=0;
float xi,yi,xf,yf,polyy[20];
printf("Coordinates of rectangular clip window :\nxmin,ymin :");
scanf("%f%f", &xmin, &ymin);
printf("xmax,ymax :");
scanf("%f%f",&xmax,&ymax);
printf("\n\nPolygon to be clipped :\nNumber of sides :");
scanf("%d",&n);
printf("Enter the coordinates :");
for(i=0;i < 2*n;i++)
scanf("%f",&polyy[i]);
polyy[i]=polyy[0];
polyy[i+1]=polyy[1];
for(i=0;i < 2*n+2;i++)
poly[i]=round(polyy[i]);
initgraph(&gdriver,&gmode,NULL);
setcolor(RED);
rectangle(xmin,ymax,xmax,ymin);
printf("\t\tUNCLIPPED POLYGON");
setcolor(WHITE);
fillpoly(n,poly);
getch();
cleardevice();
k=0;
for(i=0;i < 2*n;i+=2)
clipl(polyy[i],polyy[i+1],polyy[i+2],polyy[i+3]);
n=k/2;
for(i=0;i < k;i++)
polyy[i]=arr[i];
polyy[i]=polyy[0];
polyy[i+1]=polyy[1];
k=0;
for(i=0;i < 2*n;i+=2)
clipt(polyy[i],polyy[i+1],polyy[i+2],polyy[i+3]);
n=k/2;
for(i=0;i < k;i++)
polyy[i]=arr[i];
polyy[i]=polyy[0];
polyy[i+1]=polyy[1];
k=0;
for(i=0;i < 2*n;i+=2)
clipr(polyy[i],polyy[i+1],polyy[i+2],polyy[i+3]);
n=k/2;
for(i=0;i < k;i++)
polyy[i]=arr[i];
polyy[i]=polyy[0];
polyy[i+1]=polyy[1];
k=0;
for(i=0;i < 2*n;i+=2)
clipb(polyy[i],polyy[i+1],polyy[i+2],polyy[i+3]);
for(i=0;i < k;i++)
poly[i]=round(arr[i]);
if(k)
fillpoly(k/2,poly);
setcolor(RED);
rectangle(xmin,ymax,xmax,ymin);
printf("\tCLIPPED POLYGON");
getch();
closegraph();
}
|
code/computational_geometry/src/sutherland_hodgeman_clipping/sutherland_hodgeman_clipping.cpp | //
// main.cpp
// forfun
//
// Created by Ivan Reinaldo Liyanto on 10/5/17.
// Copyright © 2017 Ivan Reinaldo Liyanto. All rights reserved.
// Path of Cosmos by OpenGenus Foundation
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
struct coor2d
{
float x, y;
coor2d(float a, float b) : x(a), y(b)
{
}
coor2d()
{
}
};
struct edge
{
float x1, y1, x2, y2;
float xnormal, ynormal;
edge(float x1, float y1, float x2, float y2) : x1(x1), y1(y1), x2(x2), y2(y2)
{
float dx = x2 - x1;
float dy = y2 - y1;
xnormal = -dy;
ynormal = dx;
}
};
struct polygon
{
vector<coor2d> points;
polygon(const vector<coor2d> &p)
{
for (size_t i = 0; i < p.size(); i++)
points.push_back(p[i]);
}
};
bool inside(coor2d input, edge clipedge);
coor2d ComputeIntersection(coor2d a, coor2d b, edge c);
/*
* 100
*
* y
*
* 0 x 100
*/
int main()
{
//since there's normal computing involved, polygon points must be defined in clockwise manner
vector<coor2d> clipperCoords;
//example set 1
clipperCoords.push_back(coor2d(2, 5));
clipperCoords.push_back(coor2d(5, 5));
clipperCoords.push_back(coor2d(5, 1));
clipperCoords.push_back(coor2d(2, 1));
// example set 2
// clipperCoords.push_back(coor2d(5,10));
// clipperCoords.push_back(coor2d(10,1));
// clipperCoords.push_back(coor2d(0,1));
vector<coor2d> clippedCoords;
// example set 1
clippedCoords.push_back(coor2d(2, 7));
clippedCoords.push_back(coor2d(3, 7));
clippedCoords.push_back(coor2d(3, 3));
clippedCoords.push_back(coor2d(2, 3));
// example set 2
// clippedCoords.push_back(coor2d(5,5));
// clippedCoords.push_back(coor2d(15,7));
// clippedCoords.push_back(coor2d(13,1));
polygon clipper = polygon(clipperCoords);
polygon clipped = polygon(clippedCoords);
vector<coor2d> outputCoords;
vector<coor2d> inputList;
outputCoords = clipped.points;
for (size_t i = 0; i < clipper.points.size() - 1; i++)
{
inputList = outputCoords;
outputCoords.clear();
coor2d a = clipper.points[i];
coor2d b = clipper.points[i + 1];
edge clipedge = edge(a.x, a.y, b.x, b.y);
coor2d s = inputList[inputList.size() - 1];
for (size_t j = 0; j < inputList.size(); j++)
{
if (inside(inputList[j], clipedge))
{
if (!inside(s, clipedge))
outputCoords.push_back(ComputeIntersection(inputList[j], s, clipedge));
outputCoords.push_back(inputList[j]);
}
else if (inside(s, clipedge))
outputCoords.push_back(ComputeIntersection(inputList[j], s, clipedge));
s = inputList[j];
}
}
cout << "Clipped area: " << endl;
for (size_t i = 0; i < outputCoords.size(); i++)
cout << "X: " << outputCoords[i].x << " Y: " << outputCoords[i].y << endl;
return 0;
}
bool inside(coor2d input, edge clipedge)
{
coor2d a = coor2d(input.x - clipedge.x1, input.y - clipedge.y1);
float dot = a.x * clipedge.xnormal + a.y * clipedge.ynormal;
if (dot <= 0)
return true;
return false;
}
coor2d ComputeIntersection(coor2d ca, coor2d cb, edge edg)
{
float x1 = ca.x;
float x2 = cb.x;
float x3 = edg.x1;
float x4 = edg.x2;
float y1 = ca.y;
float y2 = cb.y;
float y3 = edg.y1;
float y4 = edg.y2;
float x12 = x1 - x2;
float x34 = x3 - x4;
float y12 = y1 - y2;
float y34 = y3 - y4;
float c = x12 * y34 - y12 * x34;
float a = x1 * y2 - y1 * x2;
float b = x3 * y4 - y3 * x4;
float x = (a * x34 - b * x12) / c;
float y = (a * y34 - b * y12) / c;
return coor2d(x, y);
}
|
code/computational_geometry/test/README.md | # cosmos
Your personal library of every algorithm and data structure code that you will ever encounter
|
code/computer_graphics/src/README.md | # cosmos
> Your personal library of every algorithm and data structure code that you will ever encounter
Computer Graphics is creation of pictures with the help of a computer. The end product of the computer graphics is a picture it may be a business graph, drawing, and engineering.
> Computer Graphics
Computer graphics algorithm is collectio of algorithm used to draw diffent kind on shape on the screen.
***
<p align="center">
A massive colaborative effort by
<a href="https://github.com/OpenGenus">OpenGenus Foundation</a>
</p>
***
|
code/computer_graphics/src/Transformation/2D Transformation/README.md | |
code/computer_graphics/src/Transformation/2D Transformation/Scaling/Scaling.C | #include<stdio.h>
#include<conio.h>
#include<graphics.h>
int main(){
int a[2],b[2],c[2],scale[2],i;
int gd=DETECT,gm;
initgraph(&gd,&gm,"C://TURBOC3//BGI");
printf("Enter value of a:\t");
scanf("%d%d",&a[0],&a[1]);
printf("Enter value of b:\t");
scanf("%d%d",&b[0],&b[1]);
printf("Enter value of c:\t");
scanf("%d%d",&c[0],&c[1]);
printf("Enter value of scale:\t");
scanf("%d%d",&scale[0],&scale[1]);
setcolor(RED);
line(b[0],b[1],c[0],c[1]);
line(a[0],a[1],b[0],b[1]);
line(a[0],a[1],c[0],c[1]);
setcolor(GREEN);
a[0]=scale[0]*a[0];
a[1]=scale[1]*a[1];
b[0]=scale[0]*b[0];
b[1]=scale[1]*b[1];
c[0]=scale[0]*c[0];
c[1]=scale[1]*c[1];
line(b[0],b[1],c[0],c[1]);
line(a[0],a[1],b[0],b[1]);
line(a[0],a[1],c[0],c[1]);
getch();
} |
code/computer_graphics/src/Transformation/2D Transformation/Translation/Translation.c | #include<stdio.h>
#include<graphics.h>
#include<conio.h>
int main(){
int x0,y0,x1,y1,tx,ty;
int gd=DETECT,gm;
initgraph(&gd,&gm,"C://TURBOC3//BGI");
printf("Enter coordinates of first point:\t");
scanf("%d%d",&x0,&y0);
printf("Enter coordinates of second point:\t");
scanf("%d%d",&x1,&y1);
printf("Enter coordinates of translation:\t");
scanf("%d%d",&tx,&ty);
setcolor(RED);
line(x0,y0,x1,y1);
setcolor(GREEN);
line(x0+tx,y0+ty,x1+tx,y1+ty);
printf("RED:- Initial\nGreen:- Translated")
getch();
closegraph();
}
|
code/computer_graphics/src/Transformation/README.md | # Transformation
> Transformatino is process of modifying and re-arranging the grapics.
## Types of transformation:-
2D Transformation
3D Transformation
### 2D Transformation
> In 2d Transformation we modify 2D graphics.
#### Types of 2D Transformation
1. Translation
2. Rotation
3. Scaling
4. Reflection
5. Shearing
***
<p align="center">
A massive colaborative effort by
<a href="https://github.com/OpenGenus">OpenGenus Foundation</a>
</p>
***
|
code/computer_graphics/src/circle_drawing_algorithm/bresenham's_circle_drawing_algorithm/bresenham's_circle_drawing_algorithm.c | #include<stdio.h>
#include<graphics.h>
#include<conio.h>
int main(){
int gd=DETECT,gm;
int xc,yc,x,y,r;
int x,y,p;
initgraph(&gd,&gm,"C://TURBOC3//BGI");
scanf("%d%d%d",&xc,&yc,&r);
x=0;
y=r;
p=3-2*r;
while(x<=y){
putpixel(x+xc,y+yc,WHITE);
putpixel(x+xc,-y+yc,WHITE);
putpixel(-x+xc,y+yc,WHITE);
putpixel(-x+xc,-y+yc,WHITE);
putpixel(y+xc,x+yc,WHITE);
putpixel(y+xc,-x+yc,WHITE);
putpixel(-y+xc,x+yc,WHITE);
putpixel(-y+xc,-x+yc,WHITE);
if(p<0){
x=x+1;
p=p+4*x+6;
}
else{
x=x+1;
y=y-1;
p=p+4*(x-y)+10;
}
}
getch();
closegraph();
}
|
code/computer_graphics/src/circle_drawing_algorithm/mid_point_algorithm/mid_point_algorithm.c | #include<stdio.h>
#include<graphics.h>
#include<conio.h>
int main(){
int gd=DETECT,gm;
int xc,yc,x=0,y=0,r,p;
initgraph(&gd,&gm,"C://TURBOC3//BGI");
printf("Enter center and radious:\t");
scanf("%d%d%d",&xc,&yc,&r);
p=1-r;
y=r;
cleardevice();
while(x<=y){
if(p<0){
x=x+1;
y=y;
p=p+2*x+1;
}
else{
x=x+1;
y=y-1;
p=p+2*x+1-2*y;
}
putpixel(x+xc,y+yc,WHITE);
putpixel(x+xc,-y+yc,WHITE);
putpixel(-x+xc,y+yc,WHITE);
putpixel(-x+xc,-y+yc,WHITE);
putpixel(y+xc,x+yc,WHITE);
putpixel(y+xc,-x+yc,WHITE);
putpixel(-y+xc,x+yc,WHITE);
putpixel(-y+xc,-x+yc,WHITE);
}
getch();
closegraph();
}
|
code/computer_graphics/src/diamond_square/diamond_square.py | import numpy as np
def show_as_height_map(height, mat):
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
x, y = np.meshgrid(np.arange(height), np.arange(height))
fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
ax.plot_surface(x, y, mat)
plt.title("height map")
plt.show()
def update_pixel(pixel, mean, magnitude):
return mean + (2 * pixel * magnitude) - magnitude
def main(n, smooth_factor, plot_enable):
height = (1 << n) + 1
mat = np.random.random((height, height))
i = height - 1
magnitude = 1
# seeds init
mat[0, 0] = update_pixel(mat[0, 0], 0, magnitude)
mat[0, height - 1] = update_pixel(mat[0, height - 1], 0, magnitude)
mat[height - 1, height - 1] = update_pixel(
mat[height - 1, height - 1], 0, magnitude
)
mat[0, height - 1] = update_pixel(mat[0, height - 1], 0, magnitude)
while i > 1:
id_ = i >> 1
magnitude *= smooth_factor
for xIndex in range(id_, height, i): # Beginning of the Diamond Step
for yIndex in range(id_, height, i):
mean = (
mat[xIndex - id_, yIndex - id_]
+ mat[xIndex - id_, yIndex + id_]
+ mat[xIndex + id_, yIndex + id_]
+ mat[xIndex + id_, yIndex - id_]
) / 4
mat[xIndex, yIndex] = update_pixel(mat[xIndex, yIndex], mean, magnitude)
for xIndex in range(0, height, id_): # Beginning of the Square Step
if xIndex % i == 0:
shift = id_
else:
shift = 0
for yIndex in range(shift, height, i):
sum_ = 0
n = 0
if xIndex >= id_:
sum_ += mat[xIndex - id_, yIndex]
n += 1
if xIndex + id_ < height:
sum_ += mat[xIndex + id_, yIndex]
n += 1
if yIndex >= id_:
sum_ += mat[xIndex, yIndex - id_]
n += 1
if yIndex + id_ < height:
sum_ += mat[xIndex, yIndex + id_]
n += 1
mean = sum_ / n
mat[xIndex, yIndex] = update_pixel(mat[xIndex, yIndex], mean, magnitude)
i = id_
if plot_enable:
show_as_height_map(height, mat)
return mat
def check_smooth_factor(value):
fvalue = float(value)
if fvalue < 0 or fvalue > 1:
raise argparse.ArgumentTypeError("%s is an invalid smooth factor value" % value)
return fvalue
def check_positive(value):
ivalue = int(value)
if ivalue <= 0:
raise argparse.ArgumentTypeError("%s is an invalid positive int value" % value)
return ivalue
if __name__ == "__main__":
import argparse
parser = argparse.ArgumentParser(description="machine generated calculation")
parser.add_argument(
"-n",
help="the size of the image will be 2**n + 1",
required=False,
default=8,
type=check_positive,
)
parser.add_argument(
"-s",
help="smooth factor, needs to be in range of [0, 1], value of 0 means image is very smooth,"
"value of 1 means image is very rough",
required=False,
default=0.5,
type=check_smooth_factor,
)
parser.add_argument("-p", help="plot with matplotlib", action="store_true")
args = parser.parse_args()
main(args.n, args.s, args.p)
|
code/computer_graphics/src/diamond_square/diamondsquare.java | import java.util.Scanner;
/**
* @author Samy Metadjer
* Diamond Square algorithm is a method allowing to generate
* heightmaps for computer graphics by using a 2D Grid.
*/
public class DiamondSquare{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
System.out.println("The size of your matrix needs to be 2^n+1. Enter the number n please : ");
double size = Math.pow(2, sc.nextInt())+1;
double[][] matrix = new double[(int)size][(int)size];
diamondSquare(matrix);
for(int i = 0; i < matrix.length; i++){
for(int j = 0; j < matrix.length; j++){
System.out.println("matrix[" + i + "][" + j + "] = " + matrix[i][j]);
}
}
}
/**
* Generates random value for each cell of the given array.
* @param matrix the array to be manipulated
*/
public static void diamondSquare(double[][] matrix){
int height = matrix.length;
int boundary = 40;
int i = height - 1;
int id;
int shift;
/*
** Set a random value to each corner of the matrix (Seeds values).
** It's the first square step of the algorithm
*/
matrix[0][0] = (Math.random() * (boundary - (-boundary) )) + (-boundary);
matrix[0][height-1] = (Math.random() * (boundary - (-boundary) )) + (-boundary);
matrix[height-1][0] = (Math.random() * (boundary - (-boundary) )) + (-boundary);
matrix[height-1][height-1] = (Math.random() * (boundary - (-boundary) )) + (-boundary);
while (i > 1) {
id = i / 2;
for (int xIndex = id; xIndex < height; xIndex += i) { // Beginning of the Diamond Step
for (int yIndex = id; yIndex < height; yIndex += i) {
double moyenne = (matrix[xIndex - id][yIndex - id]
+ matrix[xIndex - id][yIndex + id]
+ matrix[xIndex + id][yIndex + id]
+ matrix[xIndex + id][yIndex - id]) / 4;
matrix[xIndex][yIndex] = moyenne + (Math.random() * (height - (-height) )) + (-height);
}
}
for (int xIndex = 0; xIndex < height; xIndex += id) { // Beginning of the Square Step
if (xIndex % i == 0) {
shift = id;
} else {
shift = 0;
}
for (int yIndex = shift; yIndex < height; yIndex += i) {
int somme = 0;
int n = 0;
if (xIndex >= id) {
somme += matrix[xIndex - id][yIndex];
n += 1;
}
if (xIndex + id < height) {
somme += matrix[xIndex + id][yIndex];
n += 1;
}
if (yIndex >= id) {
somme += matrix[xIndex][yIndex - id];
n += 1;
}
if (yIndex + id < height) {
somme += matrix[xIndex][yIndex + id];
n += 1;
}
matrix[xIndex][yIndex] = somme / n + (Math.random() * (height - (-height) )) + (-height);
}
}
i = id;
}
}
}
|
code/computer_graphics/src/line_drawing_alrogrithm/Bresenham's Line Drawing Algrorithm/BDA.c | #include<stdio.h>
#include<graphics.h>
#include<conio.h>
int main(){
int x1,y1,x2,y2,dx,dy,x,y,endx,endy,p;
int gd=DETECT,gm;
initgraph(&gd,&gm,"C://TURBOC3//BGI");
printf("Enter coordinates of first point: ");
scanf("%d%d",&x1,&y1);
printf("\nEnter cooridnates of second point: ");
scanf("%d%d",&x2,&y2);
dx=x2-x1;
dy=y2-y1;
if(abs(dx)>abs(dy)){
if(x1>x2){
x=x2;
y=y2;
endx=x1;
}else{
x=x1;
y=y1;
endx=x2;
}
p=2*dy-dx;
while(x<endx){
putpixel(x,y,WHITE);
if(p<0){
p=p+2*dy;
}else{
y++;
p=p+2*dy-2*dx;
}
x++;
}
}
else{
if(y1>y2){
y=y2;
x=x2;
endy=y1;
}else{
x=x1;
y=y1;
endy=y2;
}
dx=abs(dx);
dy=abs(dy);
p=2*dx-dy;
while(y<endy){
putpixel(x,y,RED);
if(p<0){
p=p+2*dx;
}else{
x++;
p=p+2*dx-2*dy;
}
y++;
}
}
getch();
}
|
code/computer_graphics/src/line_drawing_alrogrithm/dda/dda.c | #include<stdio.h>
#include<graphics.h>
#include<conio.h>
#include<math.h>
int main(){
int gd=DETECT, gm;
float x1,y1,x2,y2;
float x,y,i;
float slope;
float dx,dy;
initgraph(&gd,&gm,"C://TURBOC3//BGI");
scanf("%f %f %f %f", &x1,&y1,&x2,&y2);
dx=x2-x1;
dy=y2-y1;
printf("%f %f", dx,dy);
if(dx>=dy) slope=dx;
else slope=dy;
dx=dx/slope;
dy=dy/slope;
x=x1;
y=y1;
i=1;
while(i<=slope){
putpixel((int)(x),(int)y,YELLOW);
x=x+dx;
y=y+dy;
i=i+1;
delay(10);
}
getch();
closegraph();
}
|
code/cryptography/src/README.md | # cosmos
> Your personal library of every algorithm and data structure code that you will ever encounter
Securing the Internet presents great challenges and research opportunities. Potential applications such as Internet voting, universally available medical records, and ubiquitous e-commerce are all being hindered because of serious security and privacy concerns. The epidemic of hacker attacks on personal computers and web sites only highlights the inherent vulnerability of the current computer and network infrastructure.
> This is where Cryptographic algorithms step in.
Cryptographic algorithms are designed around the idea of _computational hardness assumptions_, making such algorithms hard to break in practice. It is theoretically possible to break such a system but it is infeasible to do so by any known practical means. These schemes are therefore termed **computationally secure** such as improvements in integer factorization algorithms, and faster computing technology require these solutions to be continually adapted. There exist information-theoretically secure schemes that provably cannot be broken even with unlimited computing power—an example is the one-time pad—but these schemes are more difficult to implement than the best theoretically breakable but computationally secure mechanisms.
---
<p align="center">
A massive collaborative effort by <a href="https://github.com/OpenGenus/cosmos">OpenGenus Foundation</a>
</p>
---
|
code/cryptography/src/aes_128/aes_128.cpp | /*
* National University from Colombia
* Author:Andres Vargas, Jaime
* Gitub: https://github.com/jaavargasar
* webpage: https://jaavargasar.github.io/
* Language: C++
*
* Description: Given an array 1 ( outpu1 ), an array2 (output2) and a key
* we gotta decipher the messege and read what the messege is as a plane text.
* we're gonna do this with the Algorithm AES 128
*
* original plane text:Paranoia is our profession
*/
#include <iostream>
using namespace std;
//S-box
const unsigned char sbox[256] =
{0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76,
0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0,
0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15,
0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75,
0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84,
0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf,
0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8,
0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2,
0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73,
0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb,
0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08,
0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a,
0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e,
0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf,
0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16};
//Inverted S-box
const unsigned char isbox[256] =
{0x52, 0x09, 0x6a, 0xd5, 0x30, 0x36, 0xa5, 0x38, 0xbf, 0x40, 0xa3, 0x9e, 0x81, 0xf3, 0xd7, 0xfb,
0x7c, 0xe3, 0x39, 0x82, 0x9b, 0x2f, 0xff, 0x87, 0x34, 0x8e, 0x43, 0x44, 0xc4, 0xde, 0xe9, 0xcb,
0x54, 0x7b, 0x94, 0x32, 0xa6, 0xc2, 0x23, 0x3d, 0xee, 0x4c, 0x95, 0x0b, 0x42, 0xfa, 0xc3, 0x4e,
0x08, 0x2e, 0xa1, 0x66, 0x28, 0xd9, 0x24, 0xb2, 0x76, 0x5b, 0xa2, 0x49, 0x6d, 0x8b, 0xd1, 0x25,
0x72, 0xf8, 0xf6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xd4, 0xa4, 0x5c, 0xcc, 0x5d, 0x65, 0xb6, 0x92,
0x6c, 0x70, 0x48, 0x50, 0xfd, 0xed, 0xb9, 0xda, 0x5e, 0x15, 0x46, 0x57, 0xa7, 0x8d, 0x9d, 0x84,
0x90, 0xd8, 0xab, 0x00, 0x8c, 0xbc, 0xd3, 0x0a, 0xf7, 0xe4, 0x58, 0x05, 0xb8, 0xb3, 0x45, 0x06,
0xd0, 0x2c, 0x1e, 0x8f, 0xca, 0x3f, 0x0f, 0x02, 0xc1, 0xaf, 0xbd, 0x03, 0x01, 0x13, 0x8a, 0x6b,
0x3a, 0x91, 0x11, 0x41, 0x4f, 0x67, 0xdc, 0xea, 0x97, 0xf2, 0xcf, 0xce, 0xf0, 0xb4, 0xe6, 0x73,
0x96, 0xac, 0x74, 0x22, 0xe7, 0xad, 0x35, 0x85, 0xe2, 0xf9, 0x37, 0xe8, 0x1c, 0x75, 0xdf, 0x6e,
0x47, 0xf1, 0x1a, 0x71, 0x1d, 0x29, 0xc5, 0x89, 0x6f, 0xb7, 0x62, 0x0e, 0xaa, 0x18, 0xbe, 0x1b,
0xfc, 0x56, 0x3e, 0x4b, 0xc6, 0xd2, 0x79, 0x20, 0x9a, 0xdb, 0xc0, 0xfe, 0x78, 0xcd, 0x5a, 0xf4,
0x1f, 0xdd, 0xa8, 0x33, 0x88, 0x07, 0xc7, 0x31, 0xb1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xec, 0x5f,
0x60, 0x51, 0x7f, 0xa9, 0x19, 0xb5, 0x4a, 0x0d, 0x2d, 0xe5, 0x7a, 0x9f, 0x93, 0xc9, 0x9c, 0xef,
0xa0, 0xe0, 0x3b, 0x4d, 0xae, 0x2a, 0xf5, 0xb0, 0xc8, 0xeb, 0xbb, 0x3c, 0x83, 0x53, 0x99, 0x61,
0x17, 0x2b, 0x04, 0x7e, 0xba, 0x77, 0xd6, 0x26, 0xe1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0c, 0x7d};
//E Table
const unsigned char etable[256] =
{0x01, 0x03, 0x05, 0x0F, 0x11, 0x33, 0x55, 0xFF, 0x1A, 0x2E, 0x72, 0x96, 0xA1, 0xF8, 0x13, 0x35,
0x5F, 0xE1, 0x38, 0x48, 0xD8, 0x73, 0x95, 0xA4, 0xF7, 0x02, 0x06, 0x0A, 0x1E, 0x22, 0x66, 0xAA,
0xE5, 0x34, 0x5C, 0xE4, 0x37, 0x59, 0xEB, 0x26, 0x6A, 0xBE, 0xD9, 0x70, 0x90, 0xAB, 0xE6, 0x31,
0x53, 0xF5, 0x04, 0x0C, 0x14, 0x3C, 0x44, 0xCC, 0x4F, 0xD1, 0x68, 0xB8, 0xD3, 0x6E, 0xB2, 0xCD,
0x4C, 0xD4, 0x67, 0xA9, 0xE0, 0x3B, 0x4D, 0xD7, 0x62, 0xA6, 0xF1, 0x08, 0x18, 0x28, 0x78, 0x88,
0x83, 0x9E, 0xB9, 0xD0, 0x6B, 0xBD, 0xDC, 0x7F, 0x81, 0x98, 0xB3, 0xCE, 0x49, 0xDB, 0x76, 0x9A,
0xB5, 0xC4, 0x57, 0xF9, 0x10, 0x30, 0x50, 0xF0, 0x0B, 0x1D, 0x27, 0x69, 0xBB, 0xD6, 0x61, 0xA3,
0xFE, 0x19, 0x2B, 0x7D, 0x87, 0x92, 0xAD, 0xEC, 0x2F, 0x71, 0x93, 0xAE, 0xE9, 0x20, 0x60, 0xA0,
0xFB, 0x16, 0x3A, 0x4E, 0xD2, 0x6D, 0xB7, 0xC2, 0x5D, 0xE7, 0x32, 0x56, 0xFA, 0x15, 0x3F, 0x41,
0xC3, 0x5E, 0xE2, 0x3D, 0x47, 0xC9, 0x40, 0xC0, 0x5B, 0xED, 0x2C, 0x74, 0x9C, 0xBF, 0xDA, 0x75,
0x9F, 0xBA, 0xD5, 0x64, 0xAC, 0xEF, 0x2A, 0x7E, 0x82, 0x9D, 0xBC, 0xDF, 0x7A, 0x8E, 0x89, 0x80,
0x9B, 0xB6, 0xC1, 0x58, 0xE8, 0x23, 0x65, 0xAF, 0xEA, 0x25, 0x6F, 0xB1, 0xC8, 0x43, 0xC5, 0x54,
0xFC, 0x1F, 0x21, 0x63, 0xA5, 0xF4, 0x07, 0x09, 0x1B, 0x2D, 0x77, 0x99, 0xB0, 0xCB, 0x46, 0xCA,
0x45, 0xCF, 0x4A, 0xDE, 0x79, 0x8B, 0x86, 0x91, 0xA8, 0xE3, 0x3E, 0x42, 0xC6, 0x51, 0xF3, 0x0E,
0x12, 0x36, 0x5A, 0xEE, 0x29, 0x7B, 0x8D, 0x8C, 0x8F, 0x8A, 0x85, 0x94, 0xA7, 0xF2, 0x0D, 0x17,
0x39, 0x4B, 0xDD, 0x7C, 0x84, 0x97, 0xA2, 0xFD, 0x1C, 0x24, 0x6C, 0xB4, 0xC7, 0x52, 0xF6, 0x01};
//L ,Table
const unsigned char ltable[256] =
{0x00, 0x00, 0x19, 0x01, 0x32, 0x02, 0x1A, 0xC6, 0x4B, 0xC7, 0x1B, 0x68, 0x33, 0xEE, 0xDF, 0x03,
0x64, 0x04, 0xE0, 0x0E, 0x34, 0x8D, 0x81, 0xEF, 0x4C, 0x71, 0x08, 0xC8, 0xF8, 0x69, 0x1C, 0xC1,
0x7D, 0xC2, 0x1D, 0xB5, 0xF9, 0xB9, 0x27, 0x6A, 0x4D, 0xE4, 0xA6, 0x72, 0x9A, 0xC9, 0x09, 0x78,
0x65, 0x2F, 0x8A, 0x05, 0x21, 0x0F, 0xE1, 0x24, 0x12, 0xF0, 0x82, 0x45, 0x35, 0x93, 0xDA, 0x8E,
0x96, 0x8F, 0xDB, 0xBD, 0x36, 0xD0, 0xCE, 0x94, 0x13, 0x5C, 0xD2, 0xF1, 0x40, 0x46, 0x83, 0x38,
0x66, 0xDD, 0xFD, 0x30, 0xBF, 0x06, 0x8B, 0x62, 0xB3, 0x25, 0xE2, 0x98, 0x22, 0x88, 0x91, 0x10,
0x7E, 0x6E, 0x48, 0xC3, 0xA3, 0xB6, 0x1E, 0x42, 0x3A, 0x6B, 0x28, 0x54, 0xFA, 0x85, 0x3D, 0xBA,
0x2B, 0x79, 0x0A, 0x15, 0x9B, 0x9F, 0x5E, 0xCA, 0x4E, 0xD4, 0xAC, 0xE5, 0xF3, 0x73, 0xA7, 0x57,
0xAF, 0x58, 0xA8, 0x50, 0xF4, 0xEA, 0xD6, 0x74, 0x4F, 0xAE, 0xE9, 0xD5, 0xE7, 0xE6, 0xAD, 0xE8,
0x2C, 0xD7, 0x75, 0x7A, 0xEB, 0x16, 0x0B, 0xF5, 0x59, 0xCB, 0x5F, 0xB0, 0x9C, 0xA9, 0x51, 0xA0,
0x7F, 0x0C, 0xF6, 0x6F, 0x17, 0xC4, 0x49, 0xEC, 0xD8, 0x43, 0x1F, 0x2D, 0xA4, 0x76, 0x7B, 0xB7,
0xCC, 0xBB, 0x3E, 0x5A, 0xFB, 0x60, 0xB1, 0x86, 0x3B, 0x52, 0xA1, 0x6C, 0xAA, 0x55, 0x29, 0x9D,
0x97, 0xB2, 0x87, 0x90, 0x61, 0xBE, 0xDC, 0xFC, 0xBC, 0x95, 0xCF, 0xCD, 0x37, 0x3F, 0x5B, 0xD1,
0x53, 0x39, 0x84, 0x3C, 0x41, 0xA2, 0x6D, 0x47, 0x14, 0x2A, 0x9E, 0x5D, 0x56, 0xF2, 0xD3, 0xAB,
0x44, 0x11, 0x92, 0xD9, 0x23, 0x20, 0x2E, 0x89, 0xB4, 0x7C, 0xB8, 0x26, 0x77, 0x99, 0xE3, 0xA5,
0x67, 0x4A, 0xED, 0xDE, 0xC5, 0x31, 0xFE, 0x18, 0x0D, 0x63, 0x8C, 0x80, 0xC0, 0xF7, 0x70, 0x07};
const unsigned char Rcon[11] = {
0x8d, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36};
const unsigned char invMix[4][4] =
{ {0x0e, 0x0b, 0x0d, 0x09},
{0x09, 0x0e, 0x0b, 0x0d},
{0x0d, 0x09, 0x0e, 0x0b},
{0x0b, 0x0d, 0x09, 0x0e} };
unsigned char ini_keys[4][4] =
{ {0x2b, 0x28, 0xab, 0x09},
{0x7e, 0xae, 0xf7, 0xcf},
{0x15, 0xd2, 0x15, 0x4f},
{0x16, 0xa6, 0x88, 0x3c} };
unsigned char output1[4][4] =
{ {0x11, 0xe1, 0xa4, 0x50},
{0x04, 0x63, 0x26, 0x4b},
{0x14, 0x67, 0x92, 0x7d},
{0xd9, 0xce, 0x82, 0xae} };
unsigned char output2[4][4] =
{ {0xb2, 0x51, 0x2b, 0x48},
{0x7e, 0x0c, 0x11, 0xc1},
{0x32, 0x0f, 0xee, 0x38},
{0xee, 0x1a, 0x9d, 0x06} };
unsigned char keys[44][4];
// ----------------------------------- KEYS --------------------------------(begin)
//inicialize the key arrays
void init()
{
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++)
keys[i][j] = ini_keys[i][j];
}
//rotate the keys through the left
void shitrow(int pos )
{
int aux = pos + 4;
for (int i = aux; i < aux + 3; i++)
keys[i][3] = keys[++pos][3];
keys[aux + 3][3] = keys[pos - 3][3];
}
//do the subword
void subword(const int& pos)
{
int aux = pos + 4;
for (int i = aux; i < aux + 4; i++)
keys[i][3] = sbox[ keys[i][3] ];
}
//do the rcon step
void rcon(const int& pos, const int& index )
{
int aux = pos + 4;
keys[aux][3] ^= Rcon[ index];
}
//create a new round key
void newKey(int pos)
{
int org = pos;
int aux = pos + 4, ini = 3;
for (int k = 0; k < 4; k++)
{
ini = (ini + 1) % 4;
pos = org;
for (int i = aux; i < aux + 4; i++)
keys[i][ini] = ( keys[pos++][ini] ^ keys[i][ (ini + 4 - 1) % 4 ] );
}
}
//find all the posible keys
void expandkeys()
{
int cnt = 1;
for (int i = 0; i < 44; i = i + 4)
{
shitrow(i);
subword(i);
rcon(i, cnt++);
newKey(i);
}
}
void findAllKeys()
{
//we gotta find first all the keys
init();
expandkeys();
}
// ----------------------------------- KEYS --------------------------------(end)
//---------------------------------Decrypt--------------------------------(begin)
//do the add round key
void addRoundKey(int pos)
{
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++)
{
output1[i][j] ^= ( keys[pos + i][j] );
output2[i][j] ^= ( keys[pos + i][j] );
}
}
//roate the state through the right by rows
void shifrigth( )
{
for (int i = 1; i <= 2; i++)
for (int j = 3; j >= i; j--)
{
swap( output1[i][j], output1[i][j - i] );
swap( output2[i][j], output2[i][j - i] );
}
for (int j = 0; j < 3; j++)
{
swap(output1[3][j], output1[3][j + 1] );
swap(output2[3][j], output2[3][j + 1] );
}
}
// do the inverse of the subword
void invsubWord( )
{
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++)
{
output1[i][j] = isbox[ output1[i][j] ];
output2[i][j] = isbox[ output2[i][j] ];
}
}
//do galois field
unsigned char gaz(unsigned char a, unsigned char b)
{
return etable [ (ltable[a] + ltable[b]) % 0xFF ];
}
//do mix colums step
void mixColums()
{
unsigned char aux[4][4];
unsigned char aux2[4][4];
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++)
{
aux[j][i] = gaz( output1[0][i], invMix[j][0]) ^ gaz( output1[1][i], invMix[j][1]) ^ gaz(
output1[2][i], invMix[j][2]) ^ gaz( output1[3][i], invMix[j][3]);
aux2[j][i] =
gaz( output2[0][i],
invMix[j][0]) ^
gaz( output2[1][i],
invMix[j][1]) ^
gaz( output2[2][i], invMix[j][2]) ^ gaz( output2[3][i], invMix[j][3]);
}
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++)
output1[i][j] = aux[i][j];
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++)
output2[i][j] = aux2[i][j];
}
//print the state in hexadecimal
void print()
{
for (int i = 0; i < 4; i++)
{
cout << endl;
for (int j = 0; j < 4; j++)
cout << hex << output1[i][j] << " ";
//cout<<hex<<output2[i][j]<<" ";
}
cout << endl;
}
//Decipher Algorithm
void decrypt( )
{
addRoundKey(40);
shifrigth();
invsubWord();
addRoundKey(36);
for (int i = 32; i >= 0; i = i - 4)
{
mixColums();
shifrigth();
invsubWord();
addRoundKey(i);
}
}
//---------------------------------Decrypt--------------------------------(end)
//main
int main()
{
findAllKeys(); //given a initial key
decrypt(); //AES 128
//print the plan text of the output1
for (int i = 0; i < 4; i++)
{
cout << endl;
for (int j = 0; j < 4; j++)
cout << output1[j][i] << " ";
}
cout << endl;
//print plan text of output2
for (int i = 0; i < 4; i++)
{
cout << endl;
for (int j = 0; j < 4; j++)
cout << output2[j][i] << " ";
}
return 0;
}
|
code/cryptography/src/aes_128/aes_128.py | # AES 128
# By: David Beltrán (github.com/debeltranc)
# National university of Colombia
# Language: python
# This code demonstrates how AES works internally, for academic purposes only.
# If you want to use AES in your production software use robust libraries
# like PyCrypto
# Lookup tables
# Using lookup tables can help you to reduce time complexity, at cost of space complexity.
# S-box
# Used by the subBytes transformation
sBox = [
0x63,
0x7C,
0x77,
0x7B,
0xF2,
0x6B,
0x6F,
0xC5,
0x30,
0x01,
0x67,
0x2B,
0xFE,
0xD7,
0xAB,
0x76,
0xCA,
0x82,
0xC9,
0x7D,
0xFA,
0x59,
0x47,
0xF0,
0xAD,
0xD4,
0xA2,
0xAF,
0x9C,
0xA4,
0x72,
0xC0,
0xB7,
0xFD,
0x93,
0x26,
0x36,
0x3F,
0xF7,
0xCC,
0x34,
0xA5,
0xE5,
0xF1,
0x71,
0xD8,
0x31,
0x15,
0x04,
0xC7,
0x23,
0xC3,
0x18,
0x96,
0x05,
0x9A,
0x07,
0x12,
0x80,
0xE2,
0xEB,
0x27,
0xB2,
0x75,
0x09,
0x83,
0x2C,
0x1A,
0x1B,
0x6E,
0x5A,
0xA0,
0x52,
0x3B,
0xD6,
0xB3,
0x29,
0xE3,
0x2F,
0x84,
0x53,
0xD1,
0x00,
0xED,
0x20,
0xFC,
0xB1,
0x5B,
0x6A,
0xCB,
0xBE,
0x39,
0x4A,
0x4C,
0x58,
0xCF,
0xD0,
0xEF,
0xAA,
0xFB,
0x43,
0x4D,
0x33,
0x85,
0x45,
0xF9,
0x02,
0x7F,
0x50,
0x3C,
0x9F,
0xA8,
0x51,
0xA3,
0x40,
0x8F,
0x92,
0x9D,
0x38,
0xF5,
0xBC,
0xB6,
0xDA,
0x21,
0x10,
0xFF,
0xF3,
0xD2,
0xCD,
0x0C,
0x13,
0xEC,
0x5F,
0x97,
0x44,
0x17,
0xC4,
0xA7,
0x7E,
0x3D,
0x64,
0x5D,
0x19,
0x73,
0x60,
0x81,
0x4F,
0xDC,
0x22,
0x2A,
0x90,
0x88,
0x46,
0xEE,
0xB8,
0x14,
0xDE,
0x5E,
0x0B,
0xDB,
0xE0,
0x32,
0x3A,
0x0A,
0x49,
0x06,
0x24,
0x5C,
0xC2,
0xD3,
0xAC,
0x62,
0x91,
0x95,
0xE4,
0x79,
0xE7,
0xC8,
0x37,
0x6D,
0x8D,
0xD5,
0x4E,
0xA9,
0x6C,
0x56,
0xF4,
0xEA,
0x65,
0x7A,
0xAE,
0x08,
0xBA,
0x78,
0x25,
0x2E,
0x1C,
0xA6,
0xB4,
0xC6,
0xE8,
0xDD,
0x74,
0x1F,
0x4B,
0xBD,
0x8B,
0x8A,
0x70,
0x3E,
0xB5,
0x66,
0x48,
0x03,
0xF6,
0x0E,
0x61,
0x35,
0x57,
0xB9,
0x86,
0xC1,
0x1D,
0x9E,
0xE1,
0xF8,
0x98,
0x11,
0x69,
0xD9,
0x8E,
0x94,
0x9B,
0x1E,
0x87,
0xE9,
0xCE,
0x55,
0x28,
0xDF,
0x8C,
0xA1,
0x89,
0x0D,
0xBF,
0xE6,
0x42,
0x68,
0x41,
0x99,
0x2D,
0x0F,
0xB0,
0x54,
0xBB,
0x16,
]
# Inverted S-box
# Used by the invSubBytes transformation
isBox = [
0x52,
0x09,
0x6A,
0xD5,
0x30,
0x36,
0xA5,
0x38,
0xBF,
0x40,
0xA3,
0x9E,
0x81,
0xF3,
0xD7,
0xFB,
0x7C,
0xE3,
0x39,
0x82,
0x9B,
0x2F,
0xFF,
0x87,
0x34,
0x8E,
0x43,
0x44,
0xC4,
0xDE,
0xE9,
0xCB,
0x54,
0x7B,
0x94,
0x32,
0xA6,
0xC2,
0x23,
0x3D,
0xEE,
0x4C,
0x95,
0x0B,
0x42,
0xFA,
0xC3,
0x4E,
0x08,
0x2E,
0xA1,
0x66,
0x28,
0xD9,
0x24,
0xB2,
0x76,
0x5B,
0xA2,
0x49,
0x6D,
0x8B,
0xD1,
0x25,
0x72,
0xF8,
0xF6,
0x64,
0x86,
0x68,
0x98,
0x16,
0xD4,
0xA4,
0x5C,
0xCC,
0x5D,
0x65,
0xB6,
0x92,
0x6C,
0x70,
0x48,
0x50,
0xFD,
0xED,
0xB9,
0xDA,
0x5E,
0x15,
0x46,
0x57,
0xA7,
0x8D,
0x9D,
0x84,
0x90,
0xD8,
0xAB,
0x00,
0x8C,
0xBC,
0xD3,
0x0A,
0xF7,
0xE4,
0x58,
0x05,
0xB8,
0xB3,
0x45,
0x06,
0xD0,
0x2C,
0x1E,
0x8F,
0xCA,
0x3F,
0x0F,
0x02,
0xC1,
0xAF,
0xBD,
0x03,
0x01,
0x13,
0x8A,
0x6B,
0x3A,
0x91,
0x11,
0x41,
0x4F,
0x67,
0xDC,
0xEA,
0x97,
0xF2,
0xCF,
0xCE,
0xF0,
0xB4,
0xE6,
0x73,
0x96,
0xAC,
0x74,
0x22,
0xE7,
0xAD,
0x35,
0x85,
0xE2,
0xF9,
0x37,
0xE8,
0x1C,
0x75,
0xDF,
0x6E,
0x47,
0xF1,
0x1A,
0x71,
0x1D,
0x29,
0xC5,
0x89,
0x6F,
0xB7,
0x62,
0x0E,
0xAA,
0x18,
0xBE,
0x1B,
0xFC,
0x56,
0x3E,
0x4B,
0xC6,
0xD2,
0x79,
0x20,
0x9A,
0xDB,
0xC0,
0xFE,
0x78,
0xCD,
0x5A,
0xF4,
0x1F,
0xDD,
0xA8,
0x33,
0x88,
0x07,
0xC7,
0x31,
0xB1,
0x12,
0x10,
0x59,
0x27,
0x80,
0xEC,
0x5F,
0x60,
0x51,
0x7F,
0xA9,
0x19,
0xB5,
0x4A,
0x0D,
0x2D,
0xE5,
0x7A,
0x9F,
0x93,
0xC9,
0x9C,
0xEF,
0xA0,
0xE0,
0x3B,
0x4D,
0xAE,
0x2A,
0xF5,
0xB0,
0xC8,
0xEB,
0xBB,
0x3C,
0x83,
0x53,
0x99,
0x61,
0x17,
0x2B,
0x04,
0x7E,
0xBA,
0x77,
0xD6,
0x26,
0xE1,
0x69,
0x14,
0x63,
0x55,
0x21,
0x0C,
0x7D,
]
# E Table
# Used to perform Galois Field multiplications
eTable = [
0x01,
0x03,
0x05,
0x0F,
0x11,
0x33,
0x55,
0xFF,
0x1A,
0x2E,
0x72,
0x96,
0xA1,
0xF8,
0x13,
0x35,
0x5F,
0xE1,
0x38,
0x48,
0xD8,
0x73,
0x95,
0xA4,
0xF7,
0x02,
0x06,
0x0A,
0x1E,
0x22,
0x66,
0xAA,
0xE5,
0x34,
0x5C,
0xE4,
0x37,
0x59,
0xEB,
0x26,
0x6A,
0xBE,
0xD9,
0x70,
0x90,
0xAB,
0xE6,
0x31,
0x53,
0xF5,
0x04,
0x0C,
0x14,
0x3C,
0x44,
0xCC,
0x4F,
0xD1,
0x68,
0xB8,
0xD3,
0x6E,
0xB2,
0xCD,
0x4C,
0xD4,
0x67,
0xA9,
0xE0,
0x3B,
0x4D,
0xD7,
0x62,
0xA6,
0xF1,
0x08,
0x18,
0x28,
0x78,
0x88,
0x83,
0x9E,
0xB9,
0xD0,
0x6B,
0xBD,
0xDC,
0x7F,
0x81,
0x98,
0xB3,
0xCE,
0x49,
0xDB,
0x76,
0x9A,
0xB5,
0xC4,
0x57,
0xF9,
0x10,
0x30,
0x50,
0xF0,
0x0B,
0x1D,
0x27,
0x69,
0xBB,
0xD6,
0x61,
0xA3,
0xFE,
0x19,
0x2B,
0x7D,
0x87,
0x92,
0xAD,
0xEC,
0x2F,
0x71,
0x93,
0xAE,
0xE9,
0x20,
0x60,
0xA0,
0xFB,
0x16,
0x3A,
0x4E,
0xD2,
0x6D,
0xB7,
0xC2,
0x5D,
0xE7,
0x32,
0x56,
0xFA,
0x15,
0x3F,
0x41,
0xC3,
0x5E,
0xE2,
0x3D,
0x47,
0xC9,
0x40,
0xC0,
0x5B,
0xED,
0x2C,
0x74,
0x9C,
0xBF,
0xDA,
0x75,
0x9F,
0xBA,
0xD5,
0x64,
0xAC,
0xEF,
0x2A,
0x7E,
0x82,
0x9D,
0xBC,
0xDF,
0x7A,
0x8E,
0x89,
0x80,
0x9B,
0xB6,
0xC1,
0x58,
0xE8,
0x23,
0x65,
0xAF,
0xEA,
0x25,
0x6F,
0xB1,
0xC8,
0x43,
0xC5,
0x54,
0xFC,
0x1F,
0x21,
0x63,
0xA5,
0xF4,
0x07,
0x09,
0x1B,
0x2D,
0x77,
0x99,
0xB0,
0xCB,
0x46,
0xCA,
0x45,
0xCF,
0x4A,
0xDE,
0x79,
0x8B,
0x86,
0x91,
0xA8,
0xE3,
0x3E,
0x42,
0xC6,
0x51,
0xF3,
0x0E,
0x12,
0x36,
0x5A,
0xEE,
0x29,
0x7B,
0x8D,
0x8C,
0x8F,
0x8A,
0x85,
0x94,
0xA7,
0xF2,
0x0D,
0x17,
0x39,
0x4B,
0xDD,
0x7C,
0x84,
0x97,
0xA2,
0xFD,
0x1C,
0x24,
0x6C,
0xB4,
0xC7,
0x52,
0xF6,
0x01,
]
# L Table
# Used to perform Galois Field multiplications
lTable = [
None,
0x00,
0x19,
0x01,
0x32,
0x02,
0x1A,
0xC6,
0x4B,
0xC7,
0x1B,
0x68,
0x33,
0xEE,
0xDF,
0x03,
0x64,
0x04,
0xE0,
0x0E,
0x34,
0x8D,
0x81,
0xEF,
0x4C,
0x71,
0x08,
0xC8,
0xF8,
0x69,
0x1C,
0xC1,
0x7D,
0xC2,
0x1D,
0xB5,
0xF9,
0xB9,
0x27,
0x6A,
0x4D,
0xE4,
0xA6,
0x72,
0x9A,
0xC9,
0x09,
0x78,
0x65,
0x2F,
0x8A,
0x05,
0x21,
0x0F,
0xE1,
0x24,
0x12,
0xF0,
0x82,
0x45,
0x35,
0x93,
0xDA,
0x8E,
0x96,
0x8F,
0xDB,
0xBD,
0x36,
0xD0,
0xCE,
0x94,
0x13,
0x5C,
0xD2,
0xF1,
0x40,
0x46,
0x83,
0x38,
0x66,
0xDD,
0xFD,
0x30,
0xBF,
0x06,
0x8B,
0x62,
0xB3,
0x25,
0xE2,
0x98,
0x22,
0x88,
0x91,
0x10,
0x7E,
0x6E,
0x48,
0xC3,
0xA3,
0xB6,
0x1E,
0x42,
0x3A,
0x6B,
0x28,
0x54,
0xFA,
0x85,
0x3D,
0xBA,
0x2B,
0x79,
0x0A,
0x15,
0x9B,
0x9F,
0x5E,
0xCA,
0x4E,
0xD4,
0xAC,
0xE5,
0xF3,
0x73,
0xA7,
0x57,
0xAF,
0x58,
0xA8,
0x50,
0xF4,
0xEA,
0xD6,
0x74,
0x4F,
0xAE,
0xE9,
0xD5,
0xE7,
0xE6,
0xAD,
0xE8,
0x2C,
0xD7,
0x75,
0x7A,
0xEB,
0x16,
0x0B,
0xF5,
0x59,
0xCB,
0x5F,
0xB0,
0x9C,
0xA9,
0x51,
0xA0,
0x7F,
0x0C,
0xF6,
0x6F,
0x17,
0xC4,
0x49,
0xEC,
0xD8,
0x43,
0x1F,
0x2D,
0xA4,
0x76,
0x7B,
0xB7,
0xCC,
0xBB,
0x3E,
0x5A,
0xFB,
0x60,
0xB1,
0x86,
0x3B,
0x52,
0xA1,
0x6C,
0xAA,
0x55,
0x29,
0x9D,
0x97,
0xB2,
0x87,
0x90,
0x61,
0xBE,
0xDC,
0xFC,
0xBC,
0x95,
0xCF,
0xCD,
0x37,
0x3F,
0x5B,
0xD1,
0x53,
0x39,
0x84,
0x3C,
0x41,
0xA2,
0x6D,
0x47,
0x14,
0x2A,
0x9E,
0x5D,
0x56,
0xF2,
0xD3,
0xAB,
0x44,
0x11,
0x92,
0xD9,
0x23,
0x20,
0x2E,
0x89,
0xB4,
0x7C,
0xB8,
0x26,
0x77,
0x99,
0xE3,
0xA5,
0x67,
0x4A,
0xED,
0xDE,
0xC5,
0x31,
0xFE,
0x18,
0x0D,
0x63,
0x8C,
0x80,
0xC0,
0xF7,
0x70,
0x07,
]
# Lookup Functions =============================================================
# Function getInvsBox (decypher process)
# input: numerical (integer) position t look up in the Inverted S-box table.
# output: number at the position <<num>> inside the Inverted S-box table.
def getInvsBox(num):
return isBox[num]
# Function getsBox
# input: numerical (integer) position t look up in the S-box table.
# output: number at the position <<num>> inside the S-box table.
def getsBox(num):
return sBox[num]
# ===============================================================================
# Galois field multiplication =================================================
# The multiplication is simply the result of a lookup of the L-Table, followed
# by the addition of the results, followed by a lookup to the E-Table.
def gMult(a, b):
# special case check: mutiplying by zero
if a == 0x00 or b == 0x00:
return 0x00
# special case check: multiplying by one
elif a == 0x01 or b == 0x01:
return a * b
# if no special conditions, then lookup on the E-Table the result of adding
# the lookup of both operands on the L-Table modulo 255
else:
return eTable[(lTable[a] + lTable[b]) % 0xFF]
# ===============================================================================
# Functions part of the cypher and decypher processes ==========================
# SubBytes Transformation (cypher process)
# Uses an S-Box to perform byte-by-byte substitution of the State matrix (stmt).
# Purpose: (high) non-linearity, confusion by non-linear substitution.
def subBytes(stmt):
rt = []
for i in range(4):
rt.append([])
for j in range(4):
rt[i].append(getsBox(stmt[i][j]))
return rt
# InvSubBytes Transformation (decypher process)
# The InvSubBytes Transformation is another lookup table using the Inverse S-Box.
def invSubBytes(stmt):
rt = []
for i in range(4):
rt.append([])
for j in range(4):
rt[i].append(getInvsBox(stmt[i][j]))
return rt
# ShiftRow transformation (cypher process)
# The four rows of the state matrix (stmt) are shifted cyclically to the left as follows
# row 0 is not shifted
# row 1 is shifted cyclically by 1 position to the left
# row 2 is shifted cyclically by 2 positions to the left
# row 3 is shifted cyclically by 3 positions to the left
# Purpose: high diffusion through linear operation.
def shiftRows(stmt):
return [
[stmt[0][0], stmt[0][1], stmt[0][2], stmt[0][3]],
[stmt[1][1], stmt[1][2], stmt[1][3], stmt[1][0]],
[stmt[2][2], stmt[2][3], stmt[2][0], stmt[2][1]],
[stmt[3][3], stmt[3][0], stmt[3][1], stmt[3][2]],
]
# InvShiftRow Transformation (decypher process)
# The inverse of ShiftRow is obtained by shifting the rows to the right instead of the left.
def invShiftRows(stmt):
return [
[stmt[0][0], stmt[0][1], stmt[0][2], stmt[0][3]],
[stmt[1][3], stmt[1][0], stmt[1][1], stmt[1][2]],
[stmt[2][2], stmt[2][3], stmt[2][0], stmt[2][1]],
[stmt[3][1], stmt[3][2], stmt[3][3], stmt[3][0]],
]
# MixColumn Transformation (cypher process)
# Each column is treated as a polynomial over GF(2^8) and is then multiplied
# modulo (x^4)+1 with a fixed polynomial 3(x^3)+(x^2)+x+2.
# Purpose: high diffusion through linear operation.
def mixColumns(stmt):
rtmt = []
m = [
[0x02, 0x03, 0x01, 0x01],
[0x01, 0x02, 0x03, 0x01],
[0x01, 0x01, 0x02, 0x03],
[0x03, 0x01, 0x01, 0x02],
]
for i in range(4):
rtmt.append([])
for j in range(4):
rtmt[i].append(
gMult(m[i][0], stmt[0][j])
^ gMult(m[i][1], stmt[1][j])
^ gMult(m[i][2], stmt[2][j])
^ gMult(m[i][3], stmt[3][j])
)
return rtmt
# InvMixColumn Transformation (decypher process)
# The inverse of MixColumn exists because the 4×4 matrix used in MixColumn is invetible.
def InvMixColumns(stmt):
rtmt = []
# The transformation InvMixColumn is given by multiplying by the following matrix.
m = [
[0x0E, 0x0B, 0x0D, 0x09],
[0x09, 0x0E, 0x0B, 0x0D],
[0x0D, 0x09, 0x0E, 0x0B],
[0x0B, 0x0D, 0x09, 0x0E],
]
for i in range(4):
rtmt.append([])
for j in range(4):
rtmt[i].append(
gMult(m[i][0], stmt[0][j])
^ gMult(m[i][1], stmt[1][j])
^ gMult(m[i][2], stmt[2][j])
^ gMult(m[i][3], stmt[3][j])
)
return rtmt
# AddRoundKey Transformation (cypher and decypher process)
# The Round Key is bitwise XORed to the State.
def addRoundKey(stmt, rk):
rt = [[], [], [], []]
for i in range(4):
for j in range(4):
rt[i].append(stmt[i][j] ^ rk[i][j])
return rt
# ==============================================================================
# Key generation functions =====================================================
# AES-128 must first create Nr (10) subkeys as follows:
# * From a given key k arranged into a 4×4 matrix of bytes, we label the
# first four columns W[0], W[1], W[2], W[3].
# * This matrix is expanded by adding 40 more columns W[4], ... , W[43]
# which are computed recursively as follows:
# W[i] = W[i − 4] ⊕ W[i − 1] , if i ≡ 0 (mod 4) for i ∈ [4..43]
# W[i − 4] ⊕ T(W[i − 1]), otherwise for i ∈ [4..43]
# where T is the transformation of W[i − 1] obtained as follows:
# Let the elements of the column W[i − 1] be a, b, c, d. Shift these
# cyclically to obtain b, c, d, a. Now replace each of these bytes
# with the corresponding element in the S-Box from the ByteSub
# transformation to get 4 bytes e, f, g, h. Finally, compute the
# round constant r[i] = 00000010^((i−4)/4) in GF(2^8) then T(W[i − 1])
# is the columnvector (e ⊕ r[i], f, g, h)
# * The round key for the ith round consist of the columns W[4i], W[4i+1],
# W[4i + 2], W[4i + 3].
# rotWord
# The rotate operation takes a 32-bit word and rotates it eight bits to the left
# such that the high eight bits "wrap around" and become the low eight bits of the result.
def rotWord(rw):
return [rw[1], rw[2], rw[3], rw[0]]
# subWord
# The key schedule uses Rijndael's S-box.
def subWord(rw):
ret = []
for i in rw:
ret.append(getsBox(i))
return ret
# rcon
# Rcon is what the Rijndael documentation calls the exponentiation of 2 to a user-specified value.
def rcon(r, rw):
if 1 <= r <= 8:
return [rw[0] ^ (1 << (r - 1)), rw[1], rw[2], rw[3]]
elif r == 9:
return [rw[0] ^ 0x1B, rw[1], rw[2], rw[3]]
elif r == 10:
return [rw[0] ^ 0x36, rw[1], rw[2], rw[3]]
# transpose
# not really a key generation function, just a matrix transposition operation
def transpose(matrix):
return list(zip(*matrix))
# Key generation
# This function returns 10 subkeys following the Rijndael key schedule
def keyGen(keymt):
roundKeys = {
0: keymt,
1: [],
2: [],
3: [],
4: [],
5: [],
6: [],
7: [],
8: [],
9: [],
10: [],
}
for i in range(1, 11):
lrk = transpose(roundKeys[i - 1])
tr = rcon(i, subWord(rotWord(lrk[-1])))
rk = []
for j in range(4):
rk.append([])
for k in range(4):
if j == 0:
rk[j].append(tr[k] ^ lrk[j][k])
else:
rk[j].append(rk[j - 1][k] ^ lrk[j][k])
roundKeys[i] = transpose(rk)
return roundKeys
# ===============================================================================
# Single block (128 bit text) cypher and decypher operations ===================
# decypher
# inputs: cypher text as a 128-bit hex string, 128-bit hex key (as string)
# (optional) set process to true if you want to see
# all the steps of this process
# output: matrix containing clear message in hexadecimal ASCII
def decypher(ct, ky, process=False):
if process:
print("decipher process:")
c1 = ct.replace(" ", "")
k1 = ky.replace(" ", "")
keymatrix = [
[
int(k1[0] + k1[1], 16),
int(k1[8] + k1[9], 16),
int(k1[16] + k1[17], 16),
int(k1[24] + k1[25], 16),
],
[
int(k1[2] + k1[3], 16),
int(k1[10] + k1[11], 16),
int(k1[18] + k1[19], 16),
int(k1[26] + k1[27], 16),
],
[
int(k1[4] + k1[5], 16),
int(k1[12] + k1[13], 16),
int(k1[20] + k1[21], 16),
int(k1[28] + k1[29], 16),
],
[
int(k1[6] + k1[7], 16),
int(k1[14] + k1[15], 16),
int(k1[22] + k1[23], 16),
int(k1[30] + k1[31], 16),
],
]
stamatrix = [
[
int(c1[0] + c1[1], 16),
int(c1[8] + c1[9], 16),
int(c1[16] + c1[17], 16),
int(c1[24] + c1[25], 16),
],
[
int(c1[2] + c1[3], 16),
int(c1[10] + c1[11], 16),
int(c1[18] + c1[19], 16),
int(c1[26] + c1[27], 16),
],
[
int(c1[4] + c1[5], 16),
int(c1[12] + c1[13], 16),
int(c1[20] + c1[21], 16),
int(c1[28] + c1[29], 16),
],
[
int(c1[6] + c1[7], 16),
int(c1[14] + c1[15], 16),
int(c1[22] + c1[23], 16),
int(c1[30] + c1[31], 16),
],
]
rkeys = keyGen(keymatrix)
if process:
print("\n====first Stage====")
print("keys (10)")
printMatrix(rkeys[10])
print("Add round key (10)")
state = addRoundKey(stamatrix, rkeys[10])
printMatrix(state)
print("Inverse Shift Rows")
state = invShiftRows(state)
printMatrix(state)
print("Inverse Sub Bytes")
state = invSubBytes(state)
printMatrix(state)
print("\n====Second Stage====")
else:
state = invSubBytes(invShiftRows(addRoundKey(stamatrix, rkeys[10])))
for i in range(9, 0, -1):
if process:
print("keys (" + str(i) + ")")
printMatrix(rkeys[i])
print("Add round key (" + str(i) + ")")
state = addRoundKey(state, rkeys[i])
printMatrix(state)
print("Inverse Mix Columns")
state = InvMixColumns(state)
printMatrix(state)
print("Inverse Shift Rows")
state = invShiftRows(state)
printMatrix(state)
print("Inverse Sub Bytes")
state = invSubBytes(state)
printMatrix(state)
else:
state = invSubBytes(
invShiftRows(InvMixColumns(addRoundKey(state, rkeys[i])))
)
if process:
print("====Third Stage====")
print("keys (0")
printMatrix(rkeys[0])
print("Add round key (0)")
state = addRoundKey(state, rkeys[0])
printMatrix(state)
print("====Result====")
return state
else:
return addRoundKey(state, rkeys[0])
# cypher
# inputs: clear text message as an ASCII hexadecimal 128-bit string
# 128-bit hex key (as string)
# (optional) set process to true if you want to see
# all the steps of this process
# output: matrix containing the cypher text in hexadecimal representation
def cypher(mt, ky, process=False):
if process:
print("cipher process:")
m1 = mt.replace(" ", "")
k1 = ky.replace(" ", "")
keymatrix = [
[
int(k1[0] + k1[1], 16),
int(k1[8] + k1[9], 16),
int(k1[16] + k1[17], 16),
int(k1[24] + k1[25], 16),
],
[
int(k1[2] + k1[3], 16),
int(k1[10] + k1[11], 16),
int(k1[18] + k1[19], 16),
int(k1[26] + k1[27], 16),
],
[
int(k1[4] + k1[5], 16),
int(k1[12] + k1[13], 16),
int(k1[20] + k1[21], 16),
int(k1[28] + k1[29], 16),
],
[
int(k1[6] + k1[7], 16),
int(k1[14] + k1[15], 16),
int(k1[22] + k1[23], 16),
int(k1[30] + k1[31], 16),
],
]
stamatrix = [
[
int(m1[0] + m1[1], 16),
int(m1[8] + m1[9], 16),
int(m1[16] + m1[17], 16),
int(m1[24] + m1[25], 16),
],
[
int(m1[2] + m1[3], 16),
int(m1[10] + m1[11], 16),
int(m1[18] + m1[19], 16),
int(m1[26] + m1[27], 16),
],
[
int(m1[4] + m1[5], 16),
int(m1[12] + m1[13], 16),
int(m1[20] + m1[21], 16),
int(m1[28] + m1[29], 16),
],
[
int(m1[6] + m1[7], 16),
int(m1[14] + m1[15], 16),
int(m1[22] + m1[23], 16),
int(m1[30] + m1[31], 16),
],
]
rkeys = keyGen(keymatrix)
state = stamatrix
if process:
print("\n====first Stage====")
print("keys (0)")
printMatrix(rkeys[0])
print("add round key (0)")
state = addRoundKey(state, rkeys[0])
printMatrix(state)
print("\n====Second Stage====")
else:
state = addRoundKey(state, rkeys[0])
for i in range(1, 10):
if process:
print("Sub Bytes")
state = subBytes(state)
printMatrix(state)
print("Shift Rows")
state = shiftRows(state)
printMatrix(state)
print("Mix Columns")
state = mixColumns(state)
printMatrix(state)
print("keys (" + str(i) + ")")
printMatrix(rkeys[i])
print("add round key (" + str(i) + ")")
state = addRoundKey(state, rkeys[i])
printMatrix(state)
else:
state = addRoundKey(mixColumns(shiftRows(subBytes(state))), rkeys[i])
if process:
print("\n====third Stage====")
print("Sub Bytes")
state = subBytes(state)
printMatrix(state)
print("Shift Rows")
state = shiftRows(state)
printMatrix(state)
print("keys (10)")
printMatrix(rkeys[10])
print("add round key (10)")
state = addRoundKey(state, rkeys[10])
printMatrix(state)
print("====Result====")
return transpose(zip(*state))
else:
return transpose(addRoundKey(shiftRows(subBytes(state)), rkeys[10]))
# ===============================================================================
# multi block text cypher and decypher =========================================
# encryption
# inputs: clear text message and 128-bit key (as hex string)
# (optional) set process to true if you want to see
# all the steps of this process
# output: cypher text as an hexadecimal string
def encryption(message, key, process=False):
# split the array in 16 bit chunks
messageArray = hexStringChunks(message.strip())
# now encrypt the message and store it in a result matrix
cyphertextArray = list()
for msg in messageArray:
cyphertextArray.append(matrixToLinearString(cypher(msg, key, process)))
# return a string containing an hexadecimal cyphertext
return "".join(cyphertextArray)
# decryption
# inputs: cypher text and 128-bit key (as hex string)
# (optional) set process to true if you want to see
# all the steps of this process
# output: clear text as string
def decryption(cyphertext, key, process=False):
# split the array in 16 bit ckunks
# and unhandled error should appear if the text given is not a cyphertext
# not during this step but while the actual decypher is ocurring
cyphertextArray = stringChunks(cyphertext.replace(" ", ""))
# get the cleartext and store it in a result matrix
messageArray = list()
for ct in cyphertextArray:
messageArray.append(matrixToText(decypher(ct, key, process)))
# return the message, as we fill the last matrix with spaces to have full
# 128 bit blocks, strip the string before returning it
return ("".join(messageArray)).strip()
# ===============================================================================
# Formatting functions =========================================================
# Function printMatrix
# input: two-dimensional array of integers
# output: prints a matrix in console
def printMatrix(matrix):
for i in range(len(matrix)):
print("|", end=" ")
for j in range(len(matrix[i])):
print(format(matrix[i][j], "#04x"), end=" ")
print("|\n", end="")
# Function matrixToLinearString
# input: two-dimensional array of integers
# output: string containing byte-formatted hexadecimal numbers
def matrixToLinearString(matrix):
string = ""
for i in range(len(matrix)):
for j in range(len(matrix[i])):
string += format(matrix[i][j], "02x")
return string
# Function hexStringChunks
# input: string of text
# output: array containing hexadecimal representation of 16 character
# chunks of the original string, if a chunk is smaller than
# 16 characters, is filled with spaces
def hexStringChunks(string):
return [
str(string[i : 16 + i].ljust(16)[:16]).encode("utf-8").hex()
for i in range(0, len(string), 16)
]
def stringChunks(string):
return [string[i : 32 + i] for i in range(0, len(string), 32)]
def printHexArray(array):
print("[" + " ".join("0x{:02x}".format(x) for x in array) + "]")
def matrixToText(matrix):
nm = transpose(matrix)
ret = ""
for i in nm:
for j in i:
ret += format(j, "#04x")[2:]
return bytes.fromhex(ret).decode("utf-8")
# ===============================================================================
# Test use cases ===============================================================
if __name__ == "__main__":
# This case uses the following message "AES es muy facil"
# Chosen because has exactly 16 characters (128-bit string)
# translated into ASCII Hex code gives us 414553206573206d757920666163696c
# the key to use is 2b7e151628aed2a6abf7158809cf4f3c
# our expected cypher text is e448e574a374d90cc33c22af9b8eab7f
m = "41 45 53 20 65 73 20 6d 75 79 20 66 61 63 69 6c"
c = "e4 48 e5 74 a3 74 d9 0c c3 3c 22 af 9b 8e ab 7f"
k = "2b 7e 15 16 28 ae d2 a6 ab f7 15 88 09 cf 4f 3c"
newc = matrixToLinearString(cypher(m, k))
print("First use case:")
print("cypher-->\n\t" + newc)
print("decypher the result-->\n\t" + matrixToText(decypher(newc, k)))
print("check the expected cypher text-->\n\t" + matrixToText(decypher(c, k)))
# This case uses the phrase "Paranoia is our profession"
# Chosen because it has more than 16 characters (32 characters)
# the given cypher text is 110414d9e16367cea4269282504b7daeb27e32ee510c0f1a2b11ee9d48c13806
# the given key is 2b7e151628aed2a6abf7158809cf4f3c
m = "Paranoia is our profession"
c1 = "11 04 14 d9 e1 63 67 ce a4 26 92 82 50 4b 7d ae"
c2 = "b2 7e 32 ee 51 0c 0f 1a 2b 11 ee 9d 48 c1 38 06"
k = "2b 7e 15 16 28 ae d2 a6 ab f7 15 88 09 cf 4f 3c"
print("\n\nSecond use case:")
print(
"using block functions-->\n\t"
+ matrixToText(decypher(c1, k))
+ matrixToText(decypher(c2, k))
)
print("decryption using decryption function-->\n\t" + decryption(c1 + c2, k))
print("check te cypher-->\n\t" + encryption(m, k))
|
code/cryptography/src/aes_128/aes_csharp/README.md | # Implementation of AES-128, AES-192 and AES-256 in C#.
The implementation chooses the version of AES to use according to the size of the provided key.
See folder example for an example of how to cipher streams.
|
code/cryptography/src/aes_128/aes_csharp/aescipher.cs | /*
* Part of Cosmos by OpenGenus Foundation.
* Author : ABDOUS Kamel
*/
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace AES
{
public partial class AESCipher
{
// Size of MainKey will determine which version of AES to use.
// An ArgumentException is thrown in case of unknown size.
public AESCipher(byte[] MainKey)
{
this.MainKey = MainKey;
}
// Cipher a block of size AESCipher.BlockSize (see AESConsts.cs).
// The array CipherText must be of size AESCipher.BlockSize.
public void DoCipher(byte[] PlainText, byte[] CipherText)
{
byte[][] State = new byte[4][];
int i, j;
for(i = 0; i < 4; ++i)
{
State[i] = new byte[StateNB];
for (j = 0; j < StateNB; ++j)
State[i][j] = PlainText[i + StateNB * j];
}
AddRoundKey(State, 0);
for(i = 1; i < NR; ++i)
{
SubBytes(State, SubByte_SBox);
ShiftRows(State);
MixColumns(State);
AddRoundKey(State, i);
}
SubBytes(State, SubByte_SBox);
ShiftRows(State);
AddRoundKey(State, NR);
for(i = 0; i < 4; ++i)
{
for (j = 0; j < StateNB; ++j)
CipherText[i + StateNB * j] = State[i][j];
}
}
protected void SubBytes(byte[][] State, byte[,] sbox)
{
for(int i = 0; i < 4; ++i)
Helpers.SubBytes(State[i], sbox);
}
protected void ShiftRows(byte[][] State)
{
for(int i = 0; i < StateNB; ++i)
{
for (int j = 0; j < i; ++j)
Helpers.ShiftBytesLeft(State[i]);
}
}
protected void MixColumns(byte[][] State)
{
byte[][] buff = new byte[4][];
int i, j;
for(i = 0; i < 4; ++i)
{
buff[i] = new byte[StateNB];
State[i].CopyTo(buff[i], 0);
}
for(i = 0; i < StateNB; ++i)
{
State[0][i] = (byte)(GF_MulArray[buff[0][i], 0] ^ GF_MulArray[buff[1][i], 1] ^ buff[2][i] ^ buff[3][i]);
State[1][i] = (byte)(buff[0][i] ^ GF_MulArray[buff[1][i], 0] ^ GF_MulArray[buff[2][i], 1] ^ buff[3][i]);
State[2][i] = (byte)(buff[0][i] ^ buff[1][i] ^ GF_MulArray[buff[2][i], 0] ^ GF_MulArray[buff[3][i], 1]);
State[3][i] = (byte)(GF_MulArray[buff[0][i], 1] ^ buff[1][i] ^ buff[2][i] ^ GF_MulArray[buff[3][i], 0]);
}
}
protected void AddRoundKey(byte[][] State, int round)
{
uint rkey;
int cpt = 24;
for(int i = 0; i < 4; ++i)
{
rkey = RoundKeys[StateNB * round + i];
for(int j = 0; j < StateNB; ++j)
{
State[j][i] ^= (byte)((rkey >> cpt) & 0x000000ff);
cpt -= 8;
}
}
}
}
}
|
code/cryptography/src/aes_128/aes_csharp/aesconsts.cs | /*
* Part of Cosmos by OpenGenus Foundation.
* Author : ABDOUS Kamel
*/
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace AES
{
public partial class AESCipher
{
const int StateNB = 4;
public const int BlockSize = StateNB * 4;
public static readonly byte[,] SubByte_SBox =
{
{0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76},
{0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0},
{0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15},
{0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75},
{0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84},
{0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf},
{0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8},
{0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2},
{0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73},
{0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb},
{0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79},
{0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08},
{0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a},
{0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e},
{0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf},
{0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16}
};
public static readonly byte[,] InvSubBytes_SBox =
{
{0x52, 0x09, 0x6a, 0xd5, 0x30, 0x36, 0xa5, 0x38, 0xbf, 0x40, 0xa3, 0x9e, 0x81, 0xf3, 0xd7, 0xfb},
{0x7c, 0xe3, 0x39, 0x82, 0x9b, 0x2f, 0xff, 0x87, 0x34, 0x8e, 0x43, 0x44, 0xc4, 0xde, 0xe9, 0xcb},
{0x54, 0x7b, 0x94, 0x32, 0xa6, 0xc2, 0x23, 0x3d, 0xee, 0x4c, 0x95, 0x0b, 0x42, 0xfa, 0xc3, 0x4e},
{0x08, 0x2e, 0xa1, 0x66, 0x28, 0xd9, 0x24, 0xb2, 0x76, 0x5b, 0xa2, 0x49, 0x6d, 0x8b, 0xd1, 0x25},
{0x72, 0xf8, 0xf6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xd4, 0xa4, 0x5c, 0xcc, 0x5d, 0x65, 0xb6, 0x92},
{0x6c, 0x70, 0x48, 0x50, 0xfd, 0xed, 0xb9, 0xda, 0x5e, 0x15, 0x46, 0x57, 0xa7, 0x8d, 0x9d, 0x84},
{0x90, 0xd8, 0xab, 0x00, 0x8c, 0xbc, 0xd3, 0x0a, 0xf7, 0xe4, 0x58, 0x05, 0xb8, 0xb3, 0x45, 0x06},
{0xd0, 0x2c, 0x1e, 0x8f, 0xca, 0x3f, 0x0f, 0x02, 0xc1, 0xaf, 0xbd, 0x03, 0x01, 0x13, 0x8a, 0x6b},
{0x3a, 0x91, 0x11, 0x41, 0x4f, 0x67, 0xdc, 0xea, 0x97, 0xf2, 0xcf, 0xce, 0xf0, 0xb4, 0xe6, 0x73},
{0x96, 0xac, 0x74, 0x22, 0xe7, 0xad, 0x35, 0x85, 0xe2, 0xf9, 0x37, 0xe8, 0x1c, 0x75, 0xdf, 0x6e},
{0x47, 0xf1, 0x1a, 0x71, 0x1d, 0x29, 0xc5, 0x89, 0x6f, 0xb7, 0x62, 0x0e, 0xaa, 0x18, 0xbe, 0x1b},
{0xfc, 0x56, 0x3e, 0x4b, 0xc6, 0xd2, 0x79, 0x20, 0x9a, 0xdb, 0xc0, 0xfe, 0x78, 0xcd, 0x5a, 0xf4},
{0x1f, 0xdd, 0xa8, 0x33, 0x88, 0x07, 0xc7, 0x31, 0xb1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xec, 0x5f},
{0x60, 0x51, 0x7f, 0xa9, 0x19, 0xb5, 0x4a, 0x0d, 0x2d, 0xe5, 0x7a, 0x9f, 0x93, 0xc9, 0x9c, 0xef},
{0xa0, 0xe0, 0x3b, 0x4d, 0xae, 0x2a, 0xf5, 0xb0, 0xc8, 0xeb, 0xbb, 0x3c, 0x83, 0x53, 0x99, 0x61},
{0x17, 0x2b, 0x04, 0x7e, 0xba, 0x77, 0xd6, 0x26, 0xe1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0c, 0x7d}
};
// - This table stores pre-calculated values for all possible GF(2^8) calculations.This
// table is only used by the (Inv)MixColumns steps.
// USAGE: The second index (column) is the coefficient of multiplication. Only 7 different
// coefficients are used: 0x01, 0x02, 0x03, 0x09, 0x0b, 0x0d, 0x0e, but multiplication by
// 1 is negligible leaving only 6 coefficients. Each column of the table is devoted to one
// of these coefficients, in the ascending order of value, from values 0x00 to 0xFF.
// (Columns are listed double-wide to conserve vertical space.)
//
// This table was taken from : https://github.com/B-Con/crypto-algorithms/blob/master/aes.c
public static readonly byte[,] GF_MulArray =
{
{0x00,0x00,0x00,0x00,0x00,0x00},{0x02,0x03,0x09,0x0b,0x0d,0x0e},
{0x04,0x06,0x12,0x16,0x1a,0x1c},{0x06,0x05,0x1b,0x1d,0x17,0x12},
{0x08,0x0c,0x24,0x2c,0x34,0x38},{0x0a,0x0f,0x2d,0x27,0x39,0x36},
{0x0c,0x0a,0x36,0x3a,0x2e,0x24},{0x0e,0x09,0x3f,0x31,0x23,0x2a},
{0x10,0x18,0x48,0x58,0x68,0x70},{0x12,0x1b,0x41,0x53,0x65,0x7e},
{0x14,0x1e,0x5a,0x4e,0x72,0x6c},{0x16,0x1d,0x53,0x45,0x7f,0x62},
{0x18,0x14,0x6c,0x74,0x5c,0x48},{0x1a,0x17,0x65,0x7f,0x51,0x46},
{0x1c,0x12,0x7e,0x62,0x46,0x54},{0x1e,0x11,0x77,0x69,0x4b,0x5a},
{0x20,0x30,0x90,0xb0,0xd0,0xe0},{0x22,0x33,0x99,0xbb,0xdd,0xee},
{0x24,0x36,0x82,0xa6,0xca,0xfc},{0x26,0x35,0x8b,0xad,0xc7,0xf2},
{0x28,0x3c,0xb4,0x9c,0xe4,0xd8},{0x2a,0x3f,0xbd,0x97,0xe9,0xd6},
{0x2c,0x3a,0xa6,0x8a,0xfe,0xc4},{0x2e,0x39,0xaf,0x81,0xf3,0xca},
{0x30,0x28,0xd8,0xe8,0xb8,0x90},{0x32,0x2b,0xd1,0xe3,0xb5,0x9e},
{0x34,0x2e,0xca,0xfe,0xa2,0x8c},{0x36,0x2d,0xc3,0xf5,0xaf,0x82},
{0x38,0x24,0xfc,0xc4,0x8c,0xa8},{0x3a,0x27,0xf5,0xcf,0x81,0xa6},
{0x3c,0x22,0xee,0xd2,0x96,0xb4},{0x3e,0x21,0xe7,0xd9,0x9b,0xba},
{0x40,0x60,0x3b,0x7b,0xbb,0xdb},{0x42,0x63,0x32,0x70,0xb6,0xd5},
{0x44,0x66,0x29,0x6d,0xa1,0xc7},{0x46,0x65,0x20,0x66,0xac,0xc9},
{0x48,0x6c,0x1f,0x57,0x8f,0xe3},{0x4a,0x6f,0x16,0x5c,0x82,0xed},
{0x4c,0x6a,0x0d,0x41,0x95,0xff},{0x4e,0x69,0x04,0x4a,0x98,0xf1},
{0x50,0x78,0x73,0x23,0xd3,0xab},{0x52,0x7b,0x7a,0x28,0xde,0xa5},
{0x54,0x7e,0x61,0x35,0xc9,0xb7},{0x56,0x7d,0x68,0x3e,0xc4,0xb9},
{0x58,0x74,0x57,0x0f,0xe7,0x93},{0x5a,0x77,0x5e,0x04,0xea,0x9d},
{0x5c,0x72,0x45,0x19,0xfd,0x8f},{0x5e,0x71,0x4c,0x12,0xf0,0x81},
{0x60,0x50,0xab,0xcb,0x6b,0x3b},{0x62,0x53,0xa2,0xc0,0x66,0x35},
{0x64,0x56,0xb9,0xdd,0x71,0x27},{0x66,0x55,0xb0,0xd6,0x7c,0x29},
{0x68,0x5c,0x8f,0xe7,0x5f,0x03},{0x6a,0x5f,0x86,0xec,0x52,0x0d},
{0x6c,0x5a,0x9d,0xf1,0x45,0x1f},{0x6e,0x59,0x94,0xfa,0x48,0x11},
{0x70,0x48,0xe3,0x93,0x03,0x4b},{0x72,0x4b,0xea,0x98,0x0e,0x45},
{0x74,0x4e,0xf1,0x85,0x19,0x57},{0x76,0x4d,0xf8,0x8e,0x14,0x59},
{0x78,0x44,0xc7,0xbf,0x37,0x73},{0x7a,0x47,0xce,0xb4,0x3a,0x7d},
{0x7c,0x42,0xd5,0xa9,0x2d,0x6f},{0x7e,0x41,0xdc,0xa2,0x20,0x61},
{0x80,0xc0,0x76,0xf6,0x6d,0xad},{0x82,0xc3,0x7f,0xfd,0x60,0xa3},
{0x84,0xc6,0x64,0xe0,0x77,0xb1},{0x86,0xc5,0x6d,0xeb,0x7a,0xbf},
{0x88,0xcc,0x52,0xda,0x59,0x95},{0x8a,0xcf,0x5b,0xd1,0x54,0x9b},
{0x8c,0xca,0x40,0xcc,0x43,0x89},{0x8e,0xc9,0x49,0xc7,0x4e,0x87},
{0x90,0xd8,0x3e,0xae,0x05,0xdd},{0x92,0xdb,0x37,0xa5,0x08,0xd3},
{0x94,0xde,0x2c,0xb8,0x1f,0xc1},{0x96,0xdd,0x25,0xb3,0x12,0xcf},
{0x98,0xd4,0x1a,0x82,0x31,0xe5},{0x9a,0xd7,0x13,0x89,0x3c,0xeb},
{0x9c,0xd2,0x08,0x94,0x2b,0xf9},{0x9e,0xd1,0x01,0x9f,0x26,0xf7},
{0xa0,0xf0,0xe6,0x46,0xbd,0x4d},{0xa2,0xf3,0xef,0x4d,0xb0,0x43},
{0xa4,0xf6,0xf4,0x50,0xa7,0x51},{0xa6,0xf5,0xfd,0x5b,0xaa,0x5f},
{0xa8,0xfc,0xc2,0x6a,0x89,0x75},{0xaa,0xff,0xcb,0x61,0x84,0x7b},
{0xac,0xfa,0xd0,0x7c,0x93,0x69},{0xae,0xf9,0xd9,0x77,0x9e,0x67},
{0xb0,0xe8,0xae,0x1e,0xd5,0x3d},{0xb2,0xeb,0xa7,0x15,0xd8,0x33},
{0xb4,0xee,0xbc,0x08,0xcf,0x21},{0xb6,0xed,0xb5,0x03,0xc2,0x2f},
{0xb8,0xe4,0x8a,0x32,0xe1,0x05},{0xba,0xe7,0x83,0x39,0xec,0x0b},
{0xbc,0xe2,0x98,0x24,0xfb,0x19},{0xbe,0xe1,0x91,0x2f,0xf6,0x17},
{0xc0,0xa0,0x4d,0x8d,0xd6,0x76},{0xc2,0xa3,0x44,0x86,0xdb,0x78},
{0xc4,0xa6,0x5f,0x9b,0xcc,0x6a},{0xc6,0xa5,0x56,0x90,0xc1,0x64},
{0xc8,0xac,0x69,0xa1,0xe2,0x4e},{0xca,0xaf,0x60,0xaa,0xef,0x40},
{0xcc,0xaa,0x7b,0xb7,0xf8,0x52},{0xce,0xa9,0x72,0xbc,0xf5,0x5c},
{0xd0,0xb8,0x05,0xd5,0xbe,0x06},{0xd2,0xbb,0x0c,0xde,0xb3,0x08},
{0xd4,0xbe,0x17,0xc3,0xa4,0x1a},{0xd6,0xbd,0x1e,0xc8,0xa9,0x14},
{0xd8,0xb4,0x21,0xf9,0x8a,0x3e},{0xda,0xb7,0x28,0xf2,0x87,0x30},
{0xdc,0xb2,0x33,0xef,0x90,0x22},{0xde,0xb1,0x3a,0xe4,0x9d,0x2c},
{0xe0,0x90,0xdd,0x3d,0x06,0x96},{0xe2,0x93,0xd4,0x36,0x0b,0x98},
{0xe4,0x96,0xcf,0x2b,0x1c,0x8a},{0xe6,0x95,0xc6,0x20,0x11,0x84},
{0xe8,0x9c,0xf9,0x11,0x32,0xae},{0xea,0x9f,0xf0,0x1a,0x3f,0xa0},
{0xec,0x9a,0xeb,0x07,0x28,0xb2},{0xee,0x99,0xe2,0x0c,0x25,0xbc},
{0xf0,0x88,0x95,0x65,0x6e,0xe6},{0xf2,0x8b,0x9c,0x6e,0x63,0xe8},
{0xf4,0x8e,0x87,0x73,0x74,0xfa},{0xf6,0x8d,0x8e,0x78,0x79,0xf4},
{0xf8,0x84,0xb1,0x49,0x5a,0xde},{0xfa,0x87,0xb8,0x42,0x57,0xd0},
{0xfc,0x82,0xa3,0x5f,0x40,0xc2},{0xfe,0x81,0xaa,0x54,0x4d,0xcc},
{0x1b,0x9b,0xec,0xf7,0xda,0x41},{0x19,0x98,0xe5,0xfc,0xd7,0x4f},
{0x1f,0x9d,0xfe,0xe1,0xc0,0x5d},{0x1d,0x9e,0xf7,0xea,0xcd,0x53},
{0x13,0x97,0xc8,0xdb,0xee,0x79},{0x11,0x94,0xc1,0xd0,0xe3,0x77},
{0x17,0x91,0xda,0xcd,0xf4,0x65},{0x15,0x92,0xd3,0xc6,0xf9,0x6b},
{0x0b,0x83,0xa4,0xaf,0xb2,0x31},{0x09,0x80,0xad,0xa4,0xbf,0x3f},
{0x0f,0x85,0xb6,0xb9,0xa8,0x2d},{0x0d,0x86,0xbf,0xb2,0xa5,0x23},
{0x03,0x8f,0x80,0x83,0x86,0x09},{0x01,0x8c,0x89,0x88,0x8b,0x07},
{0x07,0x89,0x92,0x95,0x9c,0x15},{0x05,0x8a,0x9b,0x9e,0x91,0x1b},
{0x3b,0xab,0x7c,0x47,0x0a,0xa1},{0x39,0xa8,0x75,0x4c,0x07,0xaf},
{0x3f,0xad,0x6e,0x51,0x10,0xbd},{0x3d,0xae,0x67,0x5a,0x1d,0xb3},
{0x33,0xa7,0x58,0x6b,0x3e,0x99},{0x31,0xa4,0x51,0x60,0x33,0x97},
{0x37,0xa1,0x4a,0x7d,0x24,0x85},{0x35,0xa2,0x43,0x76,0x29,0x8b},
{0x2b,0xb3,0x34,0x1f,0x62,0xd1},{0x29,0xb0,0x3d,0x14,0x6f,0xdf},
{0x2f,0xb5,0x26,0x09,0x78,0xcd},{0x2d,0xb6,0x2f,0x02,0x75,0xc3},
{0x23,0xbf,0x10,0x33,0x56,0xe9},{0x21,0xbc,0x19,0x38,0x5b,0xe7},
{0x27,0xb9,0x02,0x25,0x4c,0xf5},{0x25,0xba,0x0b,0x2e,0x41,0xfb},
{0x5b,0xfb,0xd7,0x8c,0x61,0x9a},{0x59,0xf8,0xde,0x87,0x6c,0x94},
{0x5f,0xfd,0xc5,0x9a,0x7b,0x86},{0x5d,0xfe,0xcc,0x91,0x76,0x88},
{0x53,0xf7,0xf3,0xa0,0x55,0xa2},{0x51,0xf4,0xfa,0xab,0x58,0xac},
{0x57,0xf1,0xe1,0xb6,0x4f,0xbe},{0x55,0xf2,0xe8,0xbd,0x42,0xb0},
{0x4b,0xe3,0x9f,0xd4,0x09,0xea},{0x49,0xe0,0x96,0xdf,0x04,0xe4},
{0x4f,0xe5,0x8d,0xc2,0x13,0xf6},{0x4d,0xe6,0x84,0xc9,0x1e,0xf8},
{0x43,0xef,0xbb,0xf8,0x3d,0xd2},{0x41,0xec,0xb2,0xf3,0x30,0xdc},
{0x47,0xe9,0xa9,0xee,0x27,0xce},{0x45,0xea,0xa0,0xe5,0x2a,0xc0},
{0x7b,0xcb,0x47,0x3c,0xb1,0x7a},{0x79,0xc8,0x4e,0x37,0xbc,0x74},
{0x7f,0xcd,0x55,0x2a,0xab,0x66},{0x7d,0xce,0x5c,0x21,0xa6,0x68},
{0x73,0xc7,0x63,0x10,0x85,0x42},{0x71,0xc4,0x6a,0x1b,0x88,0x4c},
{0x77,0xc1,0x71,0x06,0x9f,0x5e},{0x75,0xc2,0x78,0x0d,0x92,0x50},
{0x6b,0xd3,0x0f,0x64,0xd9,0x0a},{0x69,0xd0,0x06,0x6f,0xd4,0x04},
{0x6f,0xd5,0x1d,0x72,0xc3,0x16},{0x6d,0xd6,0x14,0x79,0xce,0x18},
{0x63,0xdf,0x2b,0x48,0xed,0x32},{0x61,0xdc,0x22,0x43,0xe0,0x3c},
{0x67,0xd9,0x39,0x5e,0xf7,0x2e},{0x65,0xda,0x30,0x55,0xfa,0x20},
{0x9b,0x5b,0x9a,0x01,0xb7,0xec},{0x99,0x58,0x93,0x0a,0xba,0xe2},
{0x9f,0x5d,0x88,0x17,0xad,0xf0},{0x9d,0x5e,0x81,0x1c,0xa0,0xfe},
{0x93,0x57,0xbe,0x2d,0x83,0xd4},{0x91,0x54,0xb7,0x26,0x8e,0xda},
{0x97,0x51,0xac,0x3b,0x99,0xc8},{0x95,0x52,0xa5,0x30,0x94,0xc6},
{0x8b,0x43,0xd2,0x59,0xdf,0x9c},{0x89,0x40,0xdb,0x52,0xd2,0x92},
{0x8f,0x45,0xc0,0x4f,0xc5,0x80},{0x8d,0x46,0xc9,0x44,0xc8,0x8e},
{0x83,0x4f,0xf6,0x75,0xeb,0xa4},{0x81,0x4c,0xff,0x7e,0xe6,0xaa},
{0x87,0x49,0xe4,0x63,0xf1,0xb8},{0x85,0x4a,0xed,0x68,0xfc,0xb6},
{0xbb,0x6b,0x0a,0xb1,0x67,0x0c},{0xb9,0x68,0x03,0xba,0x6a,0x02},
{0xbf,0x6d,0x18,0xa7,0x7d,0x10},{0xbd,0x6e,0x11,0xac,0x70,0x1e},
{0xb3,0x67,0x2e,0x9d,0x53,0x34},{0xb1,0x64,0x27,0x96,0x5e,0x3a},
{0xb7,0x61,0x3c,0x8b,0x49,0x28},{0xb5,0x62,0x35,0x80,0x44,0x26},
{0xab,0x73,0x42,0xe9,0x0f,0x7c},{0xa9,0x70,0x4b,0xe2,0x02,0x72},
{0xaf,0x75,0x50,0xff,0x15,0x60},{0xad,0x76,0x59,0xf4,0x18,0x6e},
{0xa3,0x7f,0x66,0xc5,0x3b,0x44},{0xa1,0x7c,0x6f,0xce,0x36,0x4a},
{0xa7,0x79,0x74,0xd3,0x21,0x58},{0xa5,0x7a,0x7d,0xd8,0x2c,0x56},
{0xdb,0x3b,0xa1,0x7a,0x0c,0x37},{0xd9,0x38,0xa8,0x71,0x01,0x39},
{0xdf,0x3d,0xb3,0x6c,0x16,0x2b},{0xdd,0x3e,0xba,0x67,0x1b,0x25},
{0xd3,0x37,0x85,0x56,0x38,0x0f},{0xd1,0x34,0x8c,0x5d,0x35,0x01},
{0xd7,0x31,0x97,0x40,0x22,0x13},{0xd5,0x32,0x9e,0x4b,0x2f,0x1d},
{0xcb,0x23,0xe9,0x22,0x64,0x47},{0xc9,0x20,0xe0,0x29,0x69,0x49},
{0xcf,0x25,0xfb,0x34,0x7e,0x5b},{0xcd,0x26,0xf2,0x3f,0x73,0x55},
{0xc3,0x2f,0xcd,0x0e,0x50,0x7f},{0xc1,0x2c,0xc4,0x05,0x5d,0x71},
{0xc7,0x29,0xdf,0x18,0x4a,0x63},{0xc5,0x2a,0xd6,0x13,0x47,0x6d},
{0xfb,0x0b,0x31,0xca,0xdc,0xd7},{0xf9,0x08,0x38,0xc1,0xd1,0xd9},
{0xff,0x0d,0x23,0xdc,0xc6,0xcb},{0xfd,0x0e,0x2a,0xd7,0xcb,0xc5},
{0xf3,0x07,0x15,0xe6,0xe8,0xef},{0xf1,0x04,0x1c,0xed,0xe5,0xe1},
{0xf7,0x01,0x07,0xf0,0xf2,0xf3},{0xf5,0x02,0x0e,0xfb,0xff,0xfd},
{0xeb,0x13,0x79,0x92,0xb4,0xa7},{0xe9,0x10,0x70,0x99,0xb9,0xa9},
{0xef,0x15,0x6b,0x84,0xae,0xbb},{0xed,0x16,0x62,0x8f,0xa3,0xb5},
{0xe3,0x1f,0x5d,0xbe,0x80,0x9f},{0xe1,0x1c,0x54,0xb5,0x8d,0x91},
{0xe7,0x19,0x4f,0xa8,0x9a,0x83},{0xe5,0x1a,0x46,0xa3,0x97,0x8d}
};
}
}
|
code/cryptography/src/aes_128/aes_csharp/aesdecipher.cs | /*
* Part of Cosmos by OpenGenus Foundation.
* Author : ABDOUS Kamel
*/
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace AES
{
public partial class AESCipher
{
public void DoDecipher(byte[] CipherText, byte[] PlainText)
{
byte[][] State = new byte[4][];
int i, j;
for(i = 0; i < 4; ++i)
{
State[i] = new byte[StateNB];
for (j = 0; j < StateNB; ++j)
State[i][j] = CipherText[i + StateNB * j];
}
AddRoundKey(State, NR);
for(i = NR - 1; i > 0; --i)
{
InvShiftRows(State);
SubBytes(State, InvSubBytes_SBox);
AddRoundKey(State, i);
InvMixColumns(State);
}
InvShiftRows(State);
SubBytes(State, InvSubBytes_SBox);
AddRoundKey(State, 0);
for(i = 0; i < 4; ++i)
{
for (j = 0; j < StateNB; ++j)
PlainText[i + StateNB * j] = State[i][j];
}
}
protected void InvShiftRows(byte[][] State)
{
for(int i = 0; i < 4; ++i)
{
for(int j = 0; j < i; ++j)
Helpers.ShiftBytesRight(State[i]);
}
}
protected void InvMixColumns(byte[][] State)
{
byte[][] buff = new byte[4][];
int i, j;
for(i = 0; i < 4; ++i)
{
buff[i] = new byte[StateNB];
State[i].CopyTo(buff[i], 0);
}
for(i = 0; i < StateNB; ++i)
{
State[0][i] = (byte)(GF_MulArray[buff[0][i], 5] ^ GF_MulArray[buff[1][i], 3] ^ GF_MulArray[buff[2][i], 4] ^ GF_MulArray[buff[3][i], 2]);
State[1][i] = (byte)(GF_MulArray[buff[0][i], 2] ^ GF_MulArray[buff[1][i], 5] ^ GF_MulArray[buff[2][i], 3] ^ GF_MulArray[buff[3][i], 4]);
State[2][i] = (byte)(GF_MulArray[buff[0][i], 4] ^ GF_MulArray[buff[1][i], 2] ^ GF_MulArray[buff[2][i], 5] ^ GF_MulArray[buff[3][i], 3]);
State[3][i] = (byte)(GF_MulArray[buff[0][i], 3] ^ GF_MulArray[buff[1][i], 4] ^ GF_MulArray[buff[2][i], 2] ^ GF_MulArray[buff[3][i], 5]);
}
}
}
}
|
code/cryptography/src/aes_128/aes_csharp/aeskeygen.cs | /*
* Part of Cosmos by OpenGenus Foundation.
* Author : ABDOUS Kamel
*/
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace AES
{
public partial class AESCipher
{
byte[] vMainKey;
public byte[] MainKey
{
get
{
return vMainKey;
}
set
{
switch(value.Length)
{
case 16:
GenRoundKeys(value, 4);
break;
case 24:
GenRoundKeys(value, 6);
break;
case 32:
GenRoundKeys(value, 8);
break;
default:
throw new ArgumentException("Unknown main key size.");
}
vMainKey = value;
}
}
public uint[] RoundKeys { get; protected set; }
public int NK { get; protected set; }
public int NR { get; protected set; }
protected void GenRoundKeys(byte[] MainKey, int nk)
{
int nr = Helpers.GetAESNbRounds(nk),
i, j,
rk_size = AESCipher.StateNB * (nr + 1);
uint tmp;
byte rcon = 0x01;
RoundKeys = new uint[rk_size];
for(i = 0; i < nk; ++i)
RoundKeys[i] = (uint)((MainKey[i * 4] << 24) +
(MainKey[i * 4 + 1] << 16) +
(MainKey[i * 4 + 2] << 8) +
(MainKey[i * 4 + 3]));
while(i < rk_size)
{
tmp = RoundKeys[i - 1];
if (i % nk == 0)
{
tmp = Helpers.ShiftWordLeft(tmp);
tmp = Helpers.SubWord(tmp, AESCipher.SubByte_SBox);
tmp ^= ((uint)rcon) << 24;
rcon = Helpers.X_Time(rcon);
}
else if (nk > 6 && i % nk == 4)
tmp = Helpers.SubWord(tmp, AESCipher.SubByte_SBox);
RoundKeys[i] = tmp ^ RoundKeys[i - nk];
++i;
}
this.NK = nk;
this.NR = nr;
}
}
}
|
code/cryptography/src/aes_128/aes_csharp/example/README.md | # Example of how to cipher or decipher a stream with AES
This provides an example of how to cipher or decipher a stream with AES. Just create an instance of StreamCipher with a key, and call DoCipher or DoDecipher with streams.
|
code/cryptography/src/aes_128/aes_csharp/example/streamcipher.cs | using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.IO;
namespace AES
{
public class StreamCipher
{
AESCipher TheCipher;
public StreamCipher(byte[] MainKey)
{
TheCipher = new AESCipher(MainKey);
}
// Abstract stream ciphering
public void DoCipher(Stream Src, Stream Dest)
{
DoTheJob(Src, Dest, true);
}
public void DoDecipher(Stream Src, Stream Dest)
{
DoTheJob(Src, Dest, false);
}
private void DoTheJob(Stream Src, Stream Dest, bool Cipher)
{
if (!Src.CanRead)
throw new StreamCipherException(StreamCipherException.Code.CantRead);
if (!Dest.CanWrite)
throw new StreamCipherException(StreamCipherException.Code.CantWrite);
byte[] SrcBuff = new byte[AES.AESCipher.BlockSize],
DestBuff = new byte[AES.AESCipher.BlockSize];
int n, i;
while((n = Src.Read(SrcBuff, 0, AESCipher.BlockSize)) != 0)
{
// If we read less caracters then the size of an AES block,
// we fill remaining boxes with zeros.
for (i = n; i < AESCipher.BlockSize; ++i)
SrcBuff[i] = 0;
if (Cipher)
TheCipher.DoCipher(SrcBuff, DestBuff);
else
TheCipher.DoDecipher(SrcBuff, DestBuff);
Dest.Write(DestBuff, 0, AESCipher.BlockSize);
}
}
}
}
|
code/cryptography/src/aes_128/aes_csharp/example/streamcipherexception.cs | using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace AES
{
public class StreamCipherException : Exception
{
public enum Code
{
CantRead, CantWrite
}
public Code ErrorCode { get; set; }
public StreamCipherException(Code ErrorCode) : base()
{
this.ErrorCode = ErrorCode;
}
}
}
|
code/cryptography/src/aes_128/aes_csharp/helpers.cs | /*
* Part of Cosmos by OpenGenus Foundation.
* Author : ABDOUS Kamel
*/
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace AES
{
public class Helpers
{
// Shift all bytes left by one position.
public static void ShiftBytesLeft(byte[] bytes)
{
byte tmp = bytes[0];
int i;
for(i = 0; i < bytes.Length - 1; ++i)
bytes[i] = bytes[i + 1];
bytes[i] = tmp;
}
// Shift all bytes right by one position
public static void ShiftBytesRight(byte[] bytes)
{
byte tmp = bytes.Last();
int i;
for (i = bytes.Length - 1; i > 0; --i)
bytes[i] = bytes[i - 1];
bytes[0] = tmp;
}
public static uint ShiftWordLeft(uint word)
{
byte[] b = new byte[4];
b[0] = (byte)((word & 0xff000000) >> 24);
b[1] = (byte)((word & 0x00ff0000) >> 16);
b[2] = (byte)((word & 0x0000ff00) >> 8);
b[3] = (byte)(word & 0x000000ff);
return (uint)(b[0] + (b[3] << 8) + (b[2] << 16) + (b[1] << 24));
}
public static void SubBytes(byte[] bytes, byte[,] sbox)
{
byte row, col;
for(int i = 0; i < bytes.Length; ++i)
{
row = (byte)((bytes[i] & 0xf0) >> 4);
col = (byte)(bytes[i] & 0x0f);
bytes[i] = sbox[row, col];
}
}
public static uint SubWord(uint word, byte[,] sbox)
{
int i, row, col, cpt = 24;
uint mask = 0xff000000, ret = 0;
byte b;
for(i = 0; i < 4; ++i)
{
b = (byte)((word & mask) >> cpt);
row = (b & 0xf0) >> 4;
col = b & 0x0f;
ret += (uint)(sbox[row, col] << cpt);
mask >>= 8;
cpt -= 8;
}
return ret;
}
public static byte X_Time(byte a)
{
int tmp = a & 0x80;
a <<= 1;
if (tmp == 0x80)
a ^= 0x1b;
return a;
}
public static int GetAESNbRounds(int nk)
{
return 10 + nk - 4;
}
}
}
|
code/cryptography/src/affine_cipher/affine.cpp | /* Part of Cosmos by OpenGenus Foundation */
#include <iostream>
#include <string>
/*
* Affine Cipher: each alphabet letter is maped by a linear function to its numeric equivalent
* and converted to letter again.
*
* Let x, y, a, b ∈ Z(26)
* >> Encryption: Eĸ(x) = y ≡ a * x + b mod 26
* >> Decryption: Dĸ(y) = x ≡ a-¹ * ( y - b) mod 26
*
* with the key ĸ = (a,b), which has the restriction: gcd(a, 26) = 1.
*
*/
/*
* getChar returns the char letter in alphabet with the modulo's position
* in the ring
*/
char getChar(int n)
{
char a = 'a';
int n_ = n % 26;
if (n_ < 0)
n_ += 26; // It's necessary because e.i. -1 % 26 = -1. (In Python it works better)
return a + n_;
}
/*
* a and b are the ĸey pair (a, b)
* Recall: Encryption: Eĸ(x) = y ≡ a * x + b mod 26
*/
void crypter(std::string *plain_text, int a, int b)
{
for (auto &letter:*plain_text)
{
int letter_ = letter - 97; // 97 is the 'a' position in char
letter = getChar((a * letter_) + b);
}
}
/*
* Recall: Decryption: Dĸ(y) = x ≡ a-¹ * ( y - b) mod 26
*/
void decrypter(std::string *cipher_text, int a, int b)
{
// Supose that (a) is inversible. Let's find (a)-¹
// There is a number in the open-closed range [0, 26) such that a-¹ * (invertor) ≡ 1 mod 26
int invertor = 0;
for (auto i(0ul); i < 26; i++)
if ( (a * i) % 26 == 1)
{
invertor = i;
break;
}
for (auto &letter:*cipher_text)
{
int letter_ = letter - 97;
letter = getChar(invertor * (letter_ - b) % 26);
}
}
int main(void)
{
int a = 3, b = 6; // Remember that gcd(a, 26) must be equals to 1.
std::string text = "palavraz";
std::cout << ">>> Original plain text: " << text << std::endl;
// Encryption pass
std::cout << ">>> Encryption function with the key pair (" << a << ", " << b << ")" <<
std::endl;
crypter(&text, a, b);
std::cout << ">>> Generated cipher text: " << text << std::endl;
// Decryption pass
std::cout << ">>> Decryption function with the key pair (" << a << ", " << b << ")" <<
std::endl;
decrypter(&text, a, b);
std::cout << ">>> Decrypted plain text: " << text << std::endl;
}
|
code/cryptography/src/affine_cipher/affine.htm | <!DOCTYPE html>
<html>
<title>Affine Cipher</title>
<head>
<!--Part of Cosmos by OpenGenus Foundation
Affine Cipher: each alphabet letter is maped by a linear function to its numeric equivalent
and converted to letter again. -->
<script>
function encryption(a, b) {
for (var x = 0; x < 26; x++){
var uchar = String.fromCharCode(65 + x);
var cchar = String.fromCharCode(((a*x+b)%26) + 65);
document.write(uchar + ":" + cchar);
document.write("<br>");
}
}
encryption(5, 8);
</script>
</head>
<body>
</body>
</html>
|
code/cryptography/src/affine_cipher/affine.java | import java.util.Scanner;
/**
* Created by Phuwarin on 10/23/2017.
*/
public class Affine {
private static final Scanner SCANNER = new Scanner(System.in);
private static final int ALPHABET_SIZE = 26;
public static void main(String[] args) {
System.out.print("Type 1 for encryption and 2 for decryption then Enter >> ");
int command = getCommand();
switch (command) {
case 1:
encryption();
break;
case 2:
decryption();
break;
default:
System.out.println("Command error, pls try again.");
main(null);
}
}
private static void decryption() {
int a, aInverse = 0, b;
boolean isAOk = false;
System.out.print("Enter ciphertext which want to decryption >> ");
String ciphertext = SCANNER.next();
while (!isAOk) {
System.out.print("Enter key 'a' >> ");
a = SCANNER.nextInt();
if (gcd(a, ALPHABET_SIZE) == 1) {
isAOk = true;
aInverse = findInverse(a, ALPHABET_SIZE);
} else {
System.out.println("'a' is not ok, pls try again.");
}
}
System.out.print("Enter key 'b' >> ");
b = SCANNER.nextInt();
decrypt(aInverse, b, ciphertext);
}
private static void decrypt(int aInverse, int b, String ciphertext) {
if (ciphertext == null || ciphertext.length() <= 0) {
System.out.println("Plaintext has a problem. Bye bye :)");
return;
}
ciphertext = ciphertext.toLowerCase();
StringBuilder plaintext = new StringBuilder();
int z, j;
for (int i = 0; i < ciphertext.length(); i++) {
char agent = ciphertext.charAt(i);
z = aInverse * ((agent - 97) - b);
j = z < 0 ? minusMod(z, ALPHABET_SIZE) : z % ALPHABET_SIZE;
plaintext.append((char) ('A' + j));
}
System.out.println("Plaintext: " + plaintext);
}
private static int minusMod(int minus, int mod) {
int a = Math.abs(minus);
return (mod * ((a / mod) + 1)) - a;
}
private static int findInverse(double firstNumber, double anotherNumber) {
int a1, b1, a2, b2, r, q, temp_a2, temp_b2, n1, n2, max;
if (firstNumber > anotherNumber) {
max = (int) firstNumber;
n1 = (int) firstNumber;
n2 = (int) anotherNumber;
} else {
max = (int) anotherNumber;
n1 = (int) anotherNumber;
n2 = (int) firstNumber;
}
a1 = b2 = 1;
b1 = a2 = 0;
temp_a2 = a2;
temp_b2 = b2;
r = n1 % n2;
q = n1 / n2;
while (r != 0) {
n1 = n2;
n2 = r;
a2 = a1 - q * a2;
b2 = b1 - q * b2;
a1 = temp_a2;
b1 = temp_b2;
temp_a2 = a2;
temp_b2 = b2;
r = n1 % n2;
q = n1 / n2;
}
int result;
if (firstNumber == max) {
if (a2 < 0) {
result = (int) (a2 - anotherNumber * Math.floor(a2 / anotherNumber));
} else {
result = a2;
}
} else {
if (b2 < 0) {
result = (int) (b2 - anotherNumber * Math.floor(b2 / anotherNumber));
} else
result = b2;
}
return result;
}
private static void encryption() {
boolean isAOk = false, isBOk = false;
int a = 0, b = 0;
System.out.print("Enter plaintext which want to encryption >> ");
String plaintext = SCANNER.next();
while (!isAOk) {
System.out.print("Choose 'a' but gcd (a,26) must equal 1\n" +
"'a' might be {1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23, 25} >> ");
a = SCANNER.nextInt();
if (gcd(a, ALPHABET_SIZE) == 1) {
isAOk = true;
} else {
System.out.println("'a' is not ok, pls try again.");
}
}
while (!isBOk) {
System.out.print("Choose 'b' which number you want but not equal 1 >> ");
b = SCANNER.nextInt();
if (b != 1) {
isBOk = true;
} else {
System.out.println("'b' is not ok, pls try again.");
}
}
encrypt(a, b, plaintext);
}
private static int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
private static int getCommand() {
return SCANNER.nextInt();
}
private static void encrypt(int a, int b, String plaintext) {
if (plaintext == null || plaintext.length() <= 0) {
System.out.println("Plaintext has a problem. Bye bye :)");
return;
}
plaintext = plaintext.toLowerCase();
StringBuilder ciphertext = new StringBuilder();
for (int i = 0; i < plaintext.length(); i++) {
char agent = plaintext.charAt(i);
int value = ((a * (agent - 97) + b) % ALPHABET_SIZE);
ciphertext.append((char) (value + 97));
}
System.out.println("Ciphertext: " + ciphertext);
}
}
|
code/cryptography/src/affine_cipher/affine.py | """
Part of Cosmos by OpenGenus Foundation
Affine Cipher: each alphabet letter is maped by a linear function to its numeric equivalent
and converted to letter again.
"""
def encryption(a, b):
for x in range(26):
print(chr(x + 65) + ":" + chr((a * x + b) % 26 + 65))
encryption(5, 8)
|
code/cryptography/src/affine_cipher/affine_cipher.py | import sys, pyperclip, cryptomath, random
SYMBOLS = """ !"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\] ^_`abcdefghijklmnopqrstuvwxyz{|}~""" # note the space at the front
def main():
myMessage = """"A computer would deserve to be called intelligent if it could deceive a human into believing that it was human." -Alan Turing"""
myKey = 2023
myMode = "encrypt" # set to 'encrypt' or 'decrypt'
if myMode == "encrypt":
translated = encryptMessage(myKey, myMessage)
elif myMode == "decrypt":
translated = decryptMessage(myKey, myMessage)
print("Key: %s" % (myKey))
print("%sed text:" % (myMode.title()))
print(translated)
pyperclip.copy(translated)
print("Full %sed text copied to clipboard." % (myMode))
def getKeyParts(key):
keyA = key // len(SYMBOLS)
keyB = key % len(SYMBOLS)
return (keyA, keyB)
def checkKeys(keyA, keyB, mode):
if keyA == 1 and mode == "encrypt":
sys.exit(
"The affine cipher becomes incredibly weak when key A is set to 1. Choose a different key."
)
if keyB == 0 and mode == "encrypt":
sys.exit(
"The affine cipher becomes incredibly weak when key B is set to 0. Choose a different key."
)
if keyA < 0 or keyB < 0 or keyB > len(SYMBOLS) - 1:
sys.exit(
"Key A must be greater than 0 and Key B must be between 0 and %s."
% (len(SYMBOLS) - 1)
)
if cryptomath.gcd(keyA, len(SYMBOLS)) != 1:
sys.exit(
"Key A (%s) and the symbol set size (%s) are not relatively prime. Choose a different key."
% (keyA, len(SYMBOLS))
)
def encryptMessage(key, message):
keyA, keyB = getKeyParts(key)
checkKeys(keyA, keyB, "encrypt")
ciphertext = ""
for symbol in message:
if symbol in SYMBOLS:
# encrypt this symbol
symIndex = SYMBOLS.find(symbol)
ciphertext += SYMBOLS[(symIndex * keyA + keyB) % len(SYMBOLS)]
else:
ciphertext += symbol # just append this symbol unencrypted
return ciphertext
def decryptMessage(key, message):
keyA, keyB = getKeyParts(key)
checkKeys(keyA, keyB, "decrypt")
plaintext = ""
modInverseOfKeyA = cryptomath.findModInverse(keyA, len(SYMBOLS))
for symbol in message:
if symbol in SYMBOLS:
# decrypt this symbol
symIndex = SYMBOLS.find(symbol)
plaintext += SYMBOLS[(symIndex - keyB) * modInverseOfKeyA % len(SYMBOLS)]
else:
plaintext += symbol # just append this symbol undecrypted
return plaintext
def getRandomKey():
while True:
keyA = random.randint(2, len(SYMBOLS))
keyB = random.randint(2, len(SYMBOLS))
if cryptomath.gcd(keyA, len(SYMBOLS)) == 1:
return keyA * len(SYMBOLS) + keyB
|
code/cryptography/src/affine_cipher/affinekotlin.kt | import java.util.*
/**
* Created by Phuwarin on 10/1/2018
* Part of Cosmos by OpenGenus
*/
object AffineKotlin {
private val SCANNER = Scanner(System.`in`)
private const val ALPHABET_SIZE = 26
private val command: Int
get() = SCANNER.nextInt()
@JvmStatic
fun main(args: Array<String>) {
do {
print("Type 1 for encryption and 2 for decryption then Enter >> ")
val command = command
when (command) {
1 -> encryption()
2 -> decryption()
else -> {
println("Command error, pls try again.")
}
}
} while (command != 1 && command != 2)
}
private fun decryption() {
var a: Int
var aInverse = 0
var isAOk = false
print("Enter cipherText which want to decryption >> ")
val cipherText = SCANNER.next()
while (!isAOk) {
print("Enter key 'a' >> ")
a = SCANNER.nextInt()
if (gcd(a, ALPHABET_SIZE) == 1) {
isAOk = true
aInverse = findInverse(a.toDouble(), ALPHABET_SIZE.toDouble())
} else {
println("'a' is not ok, pls try again.")
}
}
print("Enter key 'b' >> ")
val b: Int = SCANNER.nextInt()
decrypt(aInverse, b, cipherText)
}
private fun decrypt(aInverse: Int, b: Int, cipherText: String?) {
if (cipherText == null || cipherText.isEmpty()) {
println("Plaintext has a problem. Bye bye :)")
return
}
val cipherText = cipherText.toLowerCase()
val plaintext = StringBuilder()
var z: Int
var j: Int
for (i in 0 until cipherText.length) {
val agent = cipherText[i]
z = aInverse * (agent.toInt() - 97 - b)
j = if (z < 0) minusMod(z, ALPHABET_SIZE) else z % ALPHABET_SIZE
plaintext.append(('A'.toInt() + j).toChar())
}
println("Plaintext: $plaintext")
}
private fun minusMod(minus: Int, mod: Int): Int {
val a = Math.abs(minus)
return mod * (a / mod + 1) - a
}
private fun findInverse(firstNumber: Double, anotherNumber: Double): Int {
var a1: Int
var b1: Int
var a2: Int
var b2: Int
var r: Int
var q: Int
var a2Temp: Int
var b2Temp: Int
var n1: Int
var n2: Int
val max: Int
if (firstNumber > anotherNumber) {
max = firstNumber.toInt()
n1 = firstNumber.toInt()
n2 = anotherNumber.toInt()
} else {
max = anotherNumber.toInt()
n1 = anotherNumber.toInt()
n2 = firstNumber.toInt()
}
b2 = 1
a1 = b2
a2 = 0
b1 = a2
a2Temp = a2
b2Temp = b2
r = n1 % n2
q = n1 / n2
while (r != 0) {
n1 = n2
n2 = r
a2 = a1 - q * a2
b2 = b1 - q * b2
a1 = a2Temp
b1 = b2Temp
a2Temp = a2
b2Temp = b2
r = n1 % n2
q = n1 / n2
}
val result: Int
result = if (firstNumber == max.toDouble()) {
if (a2 < 0) {
(a2 - anotherNumber * Math.floor(a2 / anotherNumber)).toInt()
} else {
a2
}
} else {
if (b2 < 0) {
(b2 - anotherNumber * Math.floor(b2 / anotherNumber)).toInt()
} else
b2
}
return result
}
private fun encryption() {
var isAOk = false
var isBOk = false
var a = 0
var b = 0
print("Enter plaintext which want to encryption >> ")
val plaintext = SCANNER.next()
while (!isAOk) {
print("Choose 'a' but gcd (a,26) must equal 1\n" + "'a' might be {1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23, 25} >> ")
a = SCANNER.nextInt()
if (gcd(a, ALPHABET_SIZE) == 1) {
isAOk = true
} else {
println("'a' is not ok, pls try again.")
}
}
while (!isBOk) {
print("Choose 'b' which number you want but not equal 1 >> ")
b = SCANNER.nextInt()
if (b != 1) {
isBOk = true
} else {
println("'b' is not ok, pls try again.")
}
}
encrypt(a, b, plaintext)
}
private fun gcd(a: Int, b: Int): Int {
return if (b == 0) a else gcd(b, a % b)
}
private fun encrypt(a: Int, b: Int, plaintext: String?) {
if (plaintext == null || plaintext.isEmpty()) {
println("Plaintext has a problem. Bye bye :)")
return
}
val plaintext = plaintext.toLowerCase()
val cipherText = StringBuilder()
for (i in 0 until plaintext.length) {
val agent = plaintext[i]
val value = (a * (agent.toInt() - 97) + b) % ALPHABET_SIZE
cipherText.append((value + 97).toChar())
}
println("cipherText: $cipherText")
}
}
|
code/cryptography/src/atbash_cipher/README.md | # Atbash Cipher
Atbash cipher is a method of encrypting messages. It is a type of monoalphabetic cipher where every letter in the original message (also known as plaintext) is mapped to it's reverse. The first letter becomes the last, the second letter becomes the second last and so on. In the latin alphabet the mapping would be as follows.
| Plain | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| ------ |---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cipher | Z | Y | X | W | V | U | T | S | R | Q | P | O | N | M | L | K | J | I | H | G | F | E | D | C | B | A |
_We only try to implement atbash cipher encryption/decryption algorithms for latin alphabet._
#### Algorithm
> For encryption
1. Read the first character of the input string.
2. If it's value is an upper case alphabet then, find out it's distance from 'A' and subtract that from 'Z'. Copy the calculated value to the corrosponding index in a new character array.
3. If it's value is a lower case alphabet then, repeat the above step with 'a' and 'z'.
4. Else copy the read character unchanged at the corrosponding index in the new character array.
5. Repeat the above steps until you read null from input string.
6. The character array at the end is the encrypted message.
> For decryption.
1. Read the first character of the input string.
2. If it's value is an upper case alphabet then, find out it's distance from 'Z' and subtract that from 'A'. Copy the calculated value to the corrosponding index in a new character array.
3. If it's value is a lower case alphabet then, repeat the above step with 'z' and 'a'.
4. Else copy the read character unchanged at the corrosponding index in the new character array.
5. Repeat the above steps until you read null from input string.
6. The character array at the end is the decrypted message.
#### Time Complexity
The time complexity for the above algorithm would be O(n), where n is the length of the input string.
|
code/cryptography/src/atbash_cipher/atbash_cipher.cpp | #include <iostream>
#include <string>
#include <cctype>
using namespace std;
//Atbash Cipher modified for English
string atbash(string s);
int main()
{
string s;
cout << "Enter message to encrypt/decrypt: ";
getline(cin, s);
cout << endl << atbash(s) << endl;
}
string atbash(string s)
{
string newstr = "";
for (size_t i = 0; i < s.length(); i++)
{
if (!isalpha(s[i]))
newstr += s[i];
else if (isupper(s[i]))
newstr += (char)('Z' - (s[i] - 'A'));
else
newstr += (char)('z' - (s[i] - 'a'));
}
return newstr;
}
|
code/cryptography/src/atbash_cipher/atbash_cipher.java | import java.util.Scanner;
public class atbash_cipher {
public static void main( String[] args) {
Scanner scan = new Scanner(System.in);
String newStr,s;
char alpha;
s = scan.nextLine();
newStr = s;
// Converting string to character array
char[] n = newStr.toCharArray();
for(int i = 0; i < s.length(); i++) {
alpha = s.charAt(i);
if(Character.isUpperCase(alpha) == true ) {
n[i] = (char) ('Z' - ( alpha - 'A' ));
} else if(Character.isLowerCase(alpha) == true ) {
n[i] = (char) ( 'z' -( alpha - 'a' ));
} else {
n[i] = alpha;
}
}
// Converting character array back to string
String cipher = new String(n);
System.out.println(cipher);
}
}
|
code/cryptography/src/atbash_cipher/atbash_cipher.py | # Part of Cosmos by OpenGenus Foundation
def cipher(plaintext):
"""
Function to encode/decode given string.
"""
cipher = list(plaintext)
for i, c in enumerate(plaintext):
if ord(c) in range(ord("a"), ord("z") + 1):
cipher[i] = chr(ord("a") + ord("z") - ord(c))
return "".join(cipher)
if __name__ == "__main__":
import sys
print cipher(sys.argv[1])
|
code/cryptography/src/autokey_cipher/README.md | # Auto Key Cipher
Auto Key Cipher is a Symmetric Polyalphabetic Substitution Cipher. This algorithm is about changing plaintext letters based on secret key letters. Each letter of the message is shifted along some alphabet positions. The number of positions is equal to the place in the alphabet of the current key letter.
## How this Algorithm works
Formula used for Encryption:
> Ei = (Pi + Ki) mod 2
Formula used for Decryption:
> Di = (Ei - Ki + 26) mod 26
**Pseudo Code**
1. Convert the Plain Text or Cipher Text to either Upper or lower(must be in one format).
2. Encryption:
3. for 0 to length(text), use above formula for Dncryption,
4. nextkey = text[i] - 'A';
5. text[i] = (text[i] - 'A' + keyvalue) % 26 + 'A';
6. Decryption:
7. for 0 to length(text), use above formula for Decryption,
8. result = (text[i] - 'A' - keyvalue) % 26 + 'A';
9. text[i] = result < 'A' ? (result + 26) : (result);
10. nextkey = text[i] - 'A';
11. Display the Results
<p align="center">
For more insights, refer to <a href="https://iq.opengenus.org/auto-key-cipher/">Auto Key Cipher</a>
</p>
---
<p align="center">
A massive collaborative effort by <a href="https://github.com/ravireddy07">me</a> at <a href="https://github.com/OpenGenus/cosmos">OpenGenus Foundation</a>
</p>
---
|
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.