problem
stringlengths 1
7.47k
| solution
stringlengths 0
13.5k
| answer
stringlengths 1
272
| problem_type
stringclasses 8
values | question_type
stringclasses 3
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 7
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
G2 In a right trapezoid $A B C D(A B \| C D)$ the angle at vertex $B$ measures $75^{\circ}$. Point $H$ is the foot of the perpendicular from point $A$ to the line $B C$. If $B H=D C$ and $A D+A H=8$, find the area of $A B C D$.
|
Solution: Produce the legs of the trapezoid until they intersect at point $E$. The triangles $A B H$ and $E C D$ are congruent (ASA). The area of $A B C D$ is equal to area of triangle $E A H$ of hypotenuse
$$
A E=A D+D E=A D+A H=8
$$
Let $M$ be the midpoint of $A E$. Then
$$
M E=M A=M H=4
$$
and $\angle A M H=30^{\circ}$. Now, the altitude from $H$ to AM equals one half of $M H$, namely 2. Finally, the area is 8 .
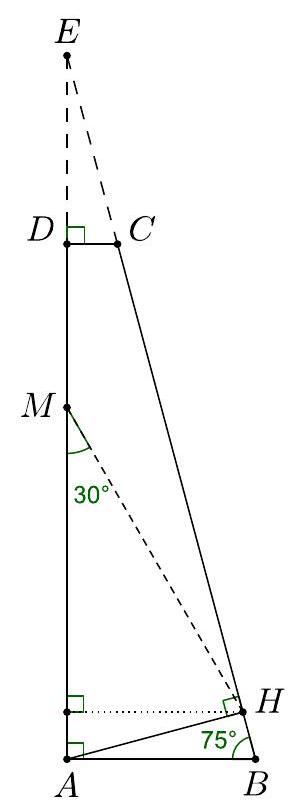
| 8 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
NT1 Determine all positive integer numbers $k$ for which the numbers $k+9$ are perfect squares and the only prime factors of $k$ are 2 and 3 .
|
Solution: We have an integer $x$ such that
$$
x^{2}=k+9
$$
$k=2^{a} 3^{b}, a, b \geq 0, a, b \in \mathbb{N}$.
Therefore,
$$
(x-3)(x+3)=k \text {. }
$$
If $b=0$ then we have $k=16$.
If $b>0$ then we have $3 \mid k+9$. Hence, $3 \mid x^{2}$ and $9 \mid k$.
Therefore, we have $b \geq 2$. Let $x=3 y$.
$$
(y-1)(y+1)=2^{a} 3^{b-2}
$$
If $a=0$ then $b=3$ and we have $k=27$.
If $a \geq 1$, then the numbers $y-1$ and $y+1$ are even. Therefore, we have $a \geq 2$, and
$$
\frac{y-1}{2} \cdot \frac{y+1}{2}=2^{a-2} 3^{b-2}
$$
Since the numbers $\frac{y-1}{2}, \frac{y+1}{2}$ are consecutive numbers, these numbers have to be powers of 2 and 3 . Let $m=a-2, n=b-2$.
- If $2^{m}-3^{n}=1$ then we have $m \geq n$. For $n=0$ we have $m=1, a=3, b=2$ and $k=72$. For $n>0$ using $\bmod 3$ we have that $m$ is even number. Let $m=2 t$. Therefore,
$$
\left(2^{t}-1\right)\left(2^{t}+1\right)=3^{n}
$$
Hence, $t=1, m=2, n=1$ and $a=4, b=3, k=432$.
- If $3^{n}-2^{m}=1$, then $m>0$. For $m=1$ we have $n=1, a=3, b=3, k=216$. For $m>1$ using $\bmod 4$ we have that $n$ is even number. Let $n=2 t$.
$$
\left(3^{t}-1\right)\left(3^{t}+1\right)=2^{m}
$$
Therefore, $t=1, n=2, m=3, a=5, b=4, k=2592$.
Set of solutions: $\{16,27,72,216,432,2592\}$.
| {16,27,72,216,432,2592} | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
NT2 A group of $n>1$ pirates of different age owned total of 2009 coins. Initially each pirate (except for the youngest one) had one coin more than the next younger.
a) Find all possible values of $n$.
b) Every day a pirate was chosen. The chosen pirate gave a coin to each of the other pirates. If $n=7$, find the largest possible number of coins a pirate can have after several days.
| ## Solution:
a) If $n$ is odd, then it is a divisor of $2009=7 \times 7 \times 41$. If $n>49$, then $n$ is at least $7 \times 41$, while the average pirate has 7 coins, so the initial division is impossible. So, we can have $n=7, n=41$ or $n=49$. Each of these cases is possible (e.g. if $n=49$, the average pirate has 41 coins, so the initial amounts are from $41-24=17$ to $41+24=65$ ).
If $n$ is even, then 2009 is multiple of the sum $S$ of the oldest and the youngest pirate. If $S<7 \times 41$, then $S$ is at most 39 and the pairs of pirates of sum $S$ is at least 41 , so we must have at least 82 pirates, a contradiction. So we can have just $S=7 \times 41=287$ and $S=49 \times 41=2009$; respectively, $n=2 \times 7=14$ or $n=2 \times 1=2$. Each of these cases is possible (e.g. if $n=14$, the initial amounts are from $144-7=137$ to $143+7=150$ ). In total, $n$ is one of the numbers $2,7,13,41$ and 49 .
b) If $n=7$, the average pirate has $7 \times 41=287$ coins, so the initial amounts are from 284 to 290; they have different residues modulo 7. The operation decreases one of the amounts by 6 and increases the other ones by 1 , so the residues will be different at all times. The largest possible amount in one pirate's possession will be achieved if all the others have as little as possible, namely $0,1,2,3,4$ and 5 coins (the residues modulo 7 have to be different). If this happens, the wealthiest pirate will have $2009-14=1994$ coins. Indeed, this can be achieved e.g. if every day (until that moment) the coins are given by the second wealthiest: while he has more than 5 coins, he can provide the 6 coins needed, and when he has no more than five, the coins at the poorest six pirates have to be $0,1,2,3,4,5$. Thus, $n=1994$ can be achieved.
| 1994 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
NT3 Find all pairs $(x, y)$ of integers which satisfy the equation
$$
(x+y)^{2}\left(x^{2}+y^{2}\right)=2009^{2}
$$
|
Solution: Let $x+y=s, x y=p$ with $s \in \mathbb{Z}^{*}$ and $p \in \mathbb{Z}$. The given equation can be written in the form
$$
s^{2}\left(s^{2}-2 p\right)=2009^{2}
$$
or
$$
s^{2}-2 p=\left(\frac{2009}{s}\right)^{2}
$$
So, $s$ divides $2009=7^{2} \times 41$ and it follows that $p \neq 0$.
If $p>0$, then $2009^{2}=s^{2}\left(s^{2}-2 p\right)=s^{4}-2 p s^{2}s^{4}$. We obtain that $s$ divides 2009 and $|s| \leq 41$. Thus, $s \in\{ \pm 1, \pm 7, \pm 41\}$. For these values of $s$ the equation has no integer solutions.
So, the given equation has only the solutions $(40,9),(9,40),(-40,-9),(-9,-40)$.
| (40,9),(9,40),(-40,-9),(-9,-40) | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
NT4 Determine all prime numbers $p_{1}, p_{2}, \ldots, p_{12}, p_{13}, p_{1} \leq p_{2} \leq \ldots \leq p_{12} \leq p_{13}$, such that
$$
p_{1}^{2}+p_{2}^{2}+\ldots+p_{12}^{2}=p_{13}^{2}
$$
and one of them is equal to $2 p_{1}+p_{9}$.
|
Solution: Obviously, $p_{13} \neq 2$, because sum of squares of 12 prime numbers is greater or equal to $12 \times 2^{2}=48$. Thus, $p_{13}$ is odd number and $p_{13} \geq 7$.
We have that $n^{2} \equiv 1(\bmod 8)$, when $n$ is odd. Let $k$ be the number of prime numbers equal to 2 . Looking at equation modulo 8 we get:
$$
4 k+12-k \equiv 1 \quad(\bmod 8)
$$
So, $k \equiv 7(\bmod 8)$ and because $k \leq 12$ we get $k=7$. Therefore, $p_{1}=p_{2}=\ldots=p_{7}=2$. Furthermore, we are looking for solutions of equations:
$$
28+p_{8}^{2}+p_{9}^{2}+p_{10}^{2}+p_{11}^{2}+p_{12}^{2}=p_{13}^{2}
$$
where $p_{8}, p_{9}, \ldots, p_{13}$ are odd prime numbers and one of them is equal to $p_{9}+4$.
Now, we know that when $n$ is not divisible by $3, n^{2} \equiv 1(\bmod 3)$. Let $s$ be number of prime numbers equal to 3 . Looking at equation modulo 3 we get:
$$
28+5-s \equiv 1 \quad(\bmod 3)
$$
Thus, $s \equiv 2(\bmod 3)$ and because $s \leq 5, s$ is either 2 or 5 . We will consider both cases. i. When $s=2$, we get $p_{8}=p_{9}=3$. Thus, we are looking for prime numbers $p_{10} \leq p_{11} \leq$ $p_{12} \leq p_{13}$ greater than 3 and at least one of them is 7 (certainly $p_{13} \neq 7$ ), that satisfy
$$
46+p_{10}^{2}+p_{11}^{2}+p_{12}^{2}=p_{13}^{2}
$$
We know that $n^{2} \equiv 1(\bmod 5)$ or $n^{2}=4(\bmod 5)$ when $n$ is not divisible by 5 . It is not possible that $p_{10}=p_{11}=5$, because in that case $p_{12}$ must be equal to 7 and the left-hand side would be divisible by 5 , which contradicts the fact that $p_{13} \geq 7$. So, we proved that $p_{10}=5$ or $p_{10}=7$.
If $p_{10}=5$ then $p_{11}=7$ because $p_{11}$ is the least of remaining prime numbers. Thus, we are looking for solutions of equation
$$
120=p_{13}^{2}-p_{12}^{2}
$$
in prime numbers. Now, from
$$
2^{3} \cdot 3 \cdot 5=\left(p_{12}-p_{12}\right)\left(p_{13}+p_{12}\right)
$$
that desired solutions are $p_{12}=7, p_{13}=13 ; p_{12}=13, p_{13}=17 ; p_{12}=29, p_{13}=31$.
If $p_{10}=7$ we are solving equation:
$$
95+p_{11}^{2}+p_{12}^{2}=p_{13}^{2}
$$
in prime numbers greater than 5 . But left side can give residues 0 or 3 modulo 5 , while right side can give only 1 or 4 modulo 5 . So, in this case we do not have solution.
ii. When $s=5$ we get equation:
$$
28+45=73=p_{13}^{2}
$$
but 73 is not square or integer and we do not have solution in this case.
Finally, only solutions are:
$\{(2,2,2,2,2,2,2,3,3,5,7,7,13),(2,2,2,2,2,2,2,3,3,5,7,13,17),(2,2,2,2,2,2,2,3,3,5,7,29,31)\}$. NT5 Show that there are infinitely many positive integers $c$, such that the following equations both have solutions in positive integers:
$$
\left(x^{2}-c\right)\left(y^{2}-c\right)=z^{2}-c
$$
and
$$
\left(x^{2}+c\right)\left(y^{2}-c\right)=z^{2}-c
$$
| (2,2,2,2,2,2,2,3,3,5,7,7,13),(2,2,2,2,2,2,2,3,3,5,7,13,17),(2,2,2,2,2,2,2,3,3,5,7,29,31) | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
C2 Can we divide an equilateral triangle $\triangle A B C$ into 2011 small triangles using 122 straight lines? (there should be 2011 triangles that are not themselves divided into smaller parts and there should be no polygons which are not triangles)
| ## Solution
Firstly, for each side of the triangle, we draw 37 equidistant, parallel lines to it. In this way we get $38^{2}=1444$ triangles. Then we erase 11 lines which are closest to the vertex $A$ and parallel to the side $B C$ and we draw 21 lines perpendicular to $B C$, the first starting from the vertex $A$ and 10 on each of the two sides, the lines which are closest to the vertex $A$, distributed symmetrically. In this way we get $26 \cdot 21+10=$ 556 new triangles. Therefore we obtain a total of 2000 triangles and we have used $37 \cdot 3-11+21=121$ lines. Let $D$ be the $12^{\text {th }}$ point on side $A B$, starting from $B$ (including it). The perpendicular to $B C$ passing through $D$ will be the last line we draw. In this way we obtain the required configuration.
| 2011 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
C4 In a group of $n$ people, each one had a different ball. They performed a sequence of swaps; in each swap, two people swapped the ball they had at that moment. Each pair of people performed at least one swap. In the end each person had the ball he/she had at the start. Find the least possible number of swaps, if: $a$ ) $n=5$; b) $n=6$.
| ## Solution
We will denote the people by $A, B, C, \ldots$ and their initial balls by the corresponding small letters. Thus the initial state is $A a, B b, C c, D d, E e(, F f)$. A swap is denoted by the (capital) letters of the people involved.
a) Five people form 10 pairs, so at least 10 swaps are necessary.
In fact, 10 swaps are sufficient:
Swap $A B$, then $B C$, then $C A$; the state is now $A a, B c, C b, D d, E e$.
Swap $A D$, then $D E$, then $E A$; the state is now $A a, B c, C b, D e, E d$.
Swap $B E$, then $C D$; the state is now $A a, B d, C e, D b, E c$.
Swap $B D$, then $C E$; the state is now $A a, B b, C c, D d, E e$.
All requirements are fulfilled now, so the answer is 10 .
b) Six people form 15 pairs, so at least 15 swaps are necessary. We will prove that the final number of swaps must be even. Call a pair formed by a ball and a person inverted if letter of the ball lies after letter of the person in the alphabet. Let $T$ be the number of inverted pairs; at the start we have $T=0$. Each swap changes $T$ by 1 , so it changes the parity of $T$. Since in the end $T=0$, the total number of swaps must be even. Hence, at least 16 swaps are necessary. In fact 16 swaps are sufficient:
Swap $A B$, then $B C$, then $C A$; the state is now $A a, B c, C b, D d, E e, F f$. Swap $A D$, then $D E$, then $E A$; the state is now $A a, B c, C b, D e, E d, F f$. Swap $F B$, then $B E$, then $E F$; the state is now $A a, B d, C b, D e, E c, F f$. Swap $F C$, then $C D$, then $D F$; the state is now $A a, B d, C e, D b, E c, F f$. Swap $B D$, then $C E$, then twice $A F$, the state is now $A a, B b, C c, D d, E e, F f$. All requirements are fulfilled now, so the answer is 16 .
| 16 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
C5 A set $S$ of natural numbers is called good, if for each element $x \in S, x$ does not divide the sum of the remaining numbers in $S$. Find the maximal possible number of elements of a good set which is a subset of the set $A=\{1,2,3, \ldots, 63\}$.
|
Solution
Let set $B$ be the good subset of $A$ which have the maximum number of elements. We can easily see that the number 1 does not belong to $B$ since 1 divides all natural numbers. Based on the property of divisibility, we know that $x$ divides the sum of the remaining numbers if and only if $x$ divides the sum of all numbers in the set $B$. If $B$ has exactly 62 elements, than $B=\{2,3,4, \ldots, 62\}$, but this set can't be good since the sum of its elements is 2015 which is divisible by 5 . Therefore $B$ has at most 61 elements. Now we are looking for the set, whose elements does not divide their sum, so the best way to do that is making a sum of elements be a prime number. $2+3+4+\ldots+63=2015$ and if we remove the number 4, we will obtain the prime number 2011. Hence the set $B=\{2,3,5,6,7, \ldots, 63\}$ is a good one. We conclude that our number is 61 .
| 61 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
C7 Consider a rectangle whose lengths of sides are natural numbers. If someone places as many squares as possible, each with area 3 , inside of the given rectangle, such that
the sides of the squares are parallel to the rectangle sides, then the maximal number of these squares fill exactly half of the area of the rectangle. Determine the dimensions of all rectangles with this property.
| ## Solution
Let $A B C D$ be a rectangle with $A B=m$ and $A D=n$ where $m, n$ are natural numbers such that $m \geq n \geq 2$. Suppose that inside of the rectangle $A B C D$ is placed a rectangular lattice consisting of some identical squares whose areas are equals to 3 , where $k$ of them are placed along the side $A B$ and $l$ of them along the side $A D$.
The sum of areas of all of this squares is equal to $3 k l$. Besides of the obvious conditions $k \sqrt{3}m$ and $(l+1) \sqrt{3}>n$ (2).
The proposed problem is to determine all pairs $(m, n) \in \mathbb{N} \times \mathbb{N}$ with $m \geq n \geq 2$, for which the ratio $R_{m, n}=\frac{3 k l}{m n}$ is equal to 0,5 where $k, l$ are natural numbers determined by the conditions (1) and (2).
Observe that for $n \geq 6$, using (2), we get $R_{m, n}=\frac{k \sqrt{3} \cdot l \sqrt{3}}{m n}>\frac{(m-\sqrt{3})(n-\sqrt{3})}{m n}=$ $\left(1-\frac{\sqrt{3}}{m}\right)\left(1-\frac{\sqrt{3}}{n}\right) \geq\left(1-\frac{\sqrt{3}}{6}\right)^{2}=\frac{1}{2}+\frac{7}{12}-\frac{\sqrt{3}}{3}>\frac{1}{2}+\frac{\sqrt{48}}{12}-\frac{\sqrt{3}}{3}=0,5$
So, the condition $R_{m, n}=0,5$ yields $n \leq 5$ or $n \in\{2,3,4,5\}$. We have 4 possible cases:
Case 1: $n=2$. Then $l=1$ and thus as above we get $R_{m, 2}=\frac{3 k}{2 m}>\frac{\sqrt{3} \cdot(m-\sqrt{3})}{2 m}=$ $\frac{\sqrt{3}}{2} \cdot\left(1-\frac{\sqrt{3}}{m}\right)$, which is greater than 0,5 for each $m>\frac{\sqrt{27}+3}{2}>\frac{5+3}{2}=4$, hence $m \in\{2,3,4\}$. Direct calculations give $R_{2,2}=R_{2,4}=0,75$ and $R_{2,3}=0,5$.
Case 2: $n=3$. Then $l=1$ and thus as above we get $R_{m, 3}=\frac{3 k}{3 m}>\frac{\sqrt{3} \cdot(m-\sqrt{3})}{3 m}=$ $\frac{\sqrt{3}}{3} \cdot\left(1-\frac{\sqrt{3}}{m}\right)$, which is greater than 0,5 for each $m>4 \sqrt{3}+6>12$, hence $m \in$ $\{3,4, \ldots, 12\}$. Direct calculations give $R_{3,3}=0,(3), R_{3,5}=0,4, R_{3,7}=4 / 7, R_{3,9}=$ $5 / 9, R_{3,11}=6 / 11$ and $R_{3,4}=R_{3,6}=R_{3,8}=R_{3,10}=R_{3,12}=0,5$.
Case 3: $n=4$. Then $l=2$ and thus as above we get $R_{m, 4}=\frac{6 k}{4 m}>\frac{\sqrt{3} \cdot(m-\sqrt{3})}{2 m}=$ $\frac{\sqrt{3}}{2} \cdot\left(1-\frac{\sqrt{3}}{m}\right)$, which is greater than 0,5 for each $m>\frac{\sqrt{27}+3}{2}>\frac{5+3}{2}=4$.
Hence $m=4$ and a calculation gives $R_{4,4}=0,75$.
Case 4: $n=5$. Then $l=2$ and thus as above we get $R_{m, 5}=\frac{6 k}{5 m}>\frac{2 \sqrt{3} \cdot(m-\sqrt{3})}{5 m}=$
$\frac{2 \sqrt{3}}{5} \cdot\left(1-\frac{\sqrt{3}}{m}\right)$, which is greater than 0,5 for each $m>\frac{12(4 \sqrt{3}+5}{23}>\frac{12 \cdot 11}{23}>6$, hence $m \in\{5,6\}$. Direct calculations give $R_{5,5}=0,48$ and $R_{5,6}=0,6$.
We conclude that: $R_{i, j}=0,5$ for $(i, j) \in\{(2,3) ;(3,4) ;(, 3,6) ;(3,8) ;(3,10) ;(3,12)\}$.
These pairs are the dimensions of all rectangles with desired property.
| (2,3);(3,4);(3,6);(3,8);(3,10);(3,12) | Geometry | math-word-problem | Yes | Yes | olympiads | false |
A2. Find all positive integers $x, y$ satisfying the equation
$$
9\left(x^{2}+y^{2}+1\right)+2(3 x y+2)=2005
$$
| ## Solution
The given equation can be written into the form
$$
2(x+y)^{2}+(x-y)^{2}=664
$$
Therefore, both numbers $x+y$ and $x-y$ are even.
Let $x+y=2 m$ and $x-y=2 t, t \in \mathbb{Z}$.
Now from (1) we have that $t$ and $t^{2}$ are even and $m$ is odd.
So, if $t=2 k, k \in \mathbb{Z}$ and $m=2 n+1, n \in \mathbb{N}$, then from (1) we get
$$
k^{2}=41-2 n(n+1)
$$
Thus $41-2 n(n+1) \geq 0$ or $2 n^{2}+2 n-41 \leq 0$. The last inequality is satisfied for the positive integers $n=1,2,3,4$ and for $n=0$.
However, only for $n=4$, equation (2) gives a perfect square $k^{2}=1 \Leftrightarrow k= \pm 1$. Therefore the solutions are $(x, y)=(11,7)$ or $(x, y)=(7,11)$.
| (x,y)=(11,7)or(x,y)=(7,11) | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
A3. Find the maximum value of the area of a triangle having side lengths $a, b, c$ with
$$
a^{2}+b^{2}+c^{2}=a^{3}+b^{3}+c^{3}
$$
| ## Solution
Without any loss of generality, we may assume that $a \leq b \leq c$.
On the one hand, Tchebyshev's inequality gives
$$
(a+b+c)\left(a^{2}+b^{2}+c^{2}\right) \leq 3\left(a^{3}+b^{3}+c^{3}\right)
$$
Therefore using the given equation we get
$$
a+b+c \leq 3 \text { or } p \leq \frac{3}{2}
$$
where $p$ denotes the semi perimeter of the triangle.
On the other hand,
$$
p=(p-a)+(p-b)+(p-c) \geq 3 \sqrt[3]{(p-a)(p-b)(p-c)}
$$
Hence
$$
\begin{aligned}
p^{3} \geq 27(p-a)(p-b)(p-c) & \Leftrightarrow p^{4} \geq 27 p(p-a)(p-b)(p-c) \\
& \Leftrightarrow p^{2} \geq 3 \sqrt{3} \cdot S
\end{aligned}
$$
where $S$ is the area of the triangle.
Thus $S \leq \frac{\sqrt{3}}{4}$ and equality holds whenever when $a=b=c=1$.
## Comment
Cauchy's inequality implies the following two inequalities are true:
$$
\frac{a+b+c}{3} \leq \frac{a^{2}+b^{2}+c^{2}}{a+b+c} \leq \frac{a^{3}+b^{3}+c^{3}}{a^{2}+b^{2}+c^{2}}
$$
Now note that
$$
\frac{a+b+c}{3} \leq \frac{a^{2}+b^{2}+c^{2}}{a+b+c}
$$
gives
$$
(a+b+c)^{2} \leq 3\left(a^{2}+b^{2}+c^{2}\right)
$$
whereas $\frac{a^{2}+b^{2}+c^{2}}{a+b+c} \leq \frac{a^{3}+b^{3}+c^{3}}{a^{2}+b^{2}+c^{2}}$, because of our assumptions, becomes $\frac{a^{2}+b^{2}+c^{2}}{a+b+c} \leq 1$, and so,
$$
a^{2}+b^{2}+c^{2} \leq a+b+c
$$
Combining (1) and (2) we get
$(a+b+c)^{2} \leq 3(a+b+c)$ and then $a+b+c \leq 3$.
| S\leq\frac{\sqrt{3}}{4} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
A4. Find all the integer solutions of the equation
$$
9 x^{2} y^{2}+9 x y^{2}+6 x^{2} y+18 x y+x^{2}+2 y^{2}+5 x+7 y+6=0
$$
| ## Solution
The equation is equivalent to the following one
$$
\begin{aligned}
& \left(9 y^{2}+6 y+1\right) x^{2}+\left(9 y^{2}+18 y+5\right) x+2 y^{2}+7 y++6=0 \\
& \Leftrightarrow(3 y+1)^{2}\left(x^{2}+x\right)+4(3 y+1) x+2 y^{2}+7 y+6=0
\end{aligned}
$$
Therefore $3 y+1$ must divide $2 y^{2}+7 y+6$ and so it must also divide
$$
9\left(2 y^{2}+7 y+6\right)=18 y^{2}+63 y+54=2(3 y+1)^{2}+17(3 y+1)+35
$$
from which it follows that it must divide 35 as well. Since $3 y+1 \in \mathbb{Z}$ we conclude that $y \in\{0,-2,2,-12\}$ and it is easy now to get all the solutions $(-2,0),(-3,0),(0,-2),(-1,2)$.
| (-2,0),(-3,0),(0,-2),(-1,2) | Algebra | math-word-problem | Yes | Yes | olympiads | false |
A5. Solve the equation
$$
8 x^{3}+8 x^{2} y+8 x y^{2}+8 y^{3}=15\left(x^{2}+y^{2}+x y+1\right)
$$
in the set of integers.
| ## Solution
We transform the equation to the following one
$$
\left(x^{2}+y^{2}\right)(8 x+8 y-15)=15(x y+1)
$$
Since the right side is divisible by 3 , then $3 /\left(x^{2}+y^{2}\right)(8 x+8 y-15)$. But if $3 /\left(x^{2}+y^{2}\right)$, then $3 / x$ and $3 / y, 009$ will wive $15(x y+1)$ and $3 /(x y+1)$, which is impossible. Hence $3 /(x+y)$ and 3 does not divide $x$ or $y$. Without loss of generality we can assume that $x=3 a+1$ and $y=3 b+2$. Substituting in the equation, we obtain
$$
\left(x^{2}+y^{2}\right)(8(a+b)+3)=5(x y+1)
$$
Since $x y+1 \equiv 0(\bmod 3)$, we conclude that $3 /(a+b)$.
Now we distinguish the following cases:
- If $a+b=0$, then $x=3 a+1$ and $y=-3 a+2$ from which we get
$$
\left(9 a^{2}+6 a+1+9 a^{2}-12 a+4\right) \cdot 3=5\left(-9 a^{2}+3 a+3\right) \text { or } 3 a^{2}-a=0
$$
But $a=\frac{1}{3}$ is not an integer, so $a=0$ and $x=1, y=2$. Thus, by symmetry, we have two solutions $(x, y)=(1,2)$ and $(x, y)=(2,1)$.
- If $a+b \neq 0$, then $|8(a+b)+3| \geq 21$. So we obtain
$$
\left|\left(x^{2}+y^{2}\right)(8(a+b)+3)\right| \geq 21 x^{2}+21 y^{2} \geq|5 x y+5|
$$
which means that the equation has no other solutions.
## Geometry
| (x,y)=(1,2)(x,y)=(2,1) | Algebra | math-word-problem | Yes | Yes | olympiads | false |
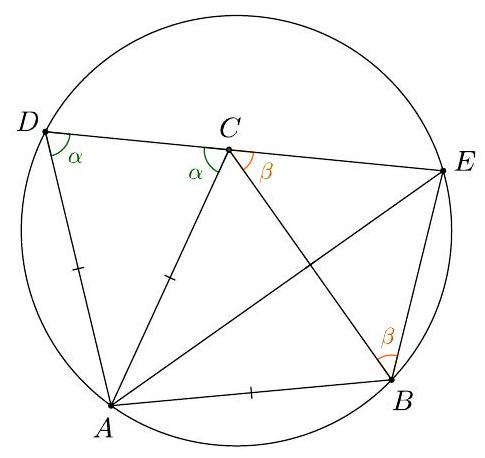
G3. Let $A B C D E F$ be a regular hexagon. The points $\mathrm{M}$ and $\mathrm{N}$ are internal points of the sides $\mathrm{DE}$ and $\mathrm{DC}$ respectively, such that $\angle A M N=90^{\circ}$ and $A N=\sqrt{2} \cdot C M$. Find the measure of the angle $\angle B A M$.
| ## Solution
Since $A C \perp C D$ and $A M \perp M N$ the quadrilateral $A M N C$ is inscribed. So, we have
$$
\angle M A N=\angle M C N
$$
Let $P$ be the projection of the point $M$ on the line $C D$. The triangles $A M N$ and $C P M$ are similar implying
$$
\frac{A M}{C P}=\frac{M N}{P M}=\frac{A N}{C M}=\sqrt{2}
$$
So, we have
$$
\frac{M P}{M N}=\frac{1}{\sqrt{2}} \Rightarrow \angle M N P=45^{\circ}
$$
Figure 4
Hence we have
$$
\angle C A M=\angle M N P=45^{\circ}
$$
and finally, we obtain
$$
\angle B A M=\angle B A C+\angle C A M=75^{\circ}
$$
| 75 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
G6. A point $O$ and the circles $k_{1}$ with center $O$ and radius $3, k_{2}$ with center $O$ and radius 5, are given. Let $A$ be a point on $k_{1}$ and $B$ be a point on $k_{2}$. If $A B C$ is equilateral triangle, find the maximum value of the distance $O C$.
| ## Solution
It is easy to see that the points $O$ and $C$ must be in different semi-planes with respect to the line $A B$.
Let $O P B$ be an equilateral triangle ( $P$ and $C$ on the same side of $O B$ ). Since $\angle P B C$ $=60^{\circ}-\angle A B P$ and $\angle O B A=60^{\circ}-\angle A B P$, then $\angle P B C=\angle O B A$. Hence the triangles $A O B$ and $C P B$ are equal and $P C=O A$. From the triangle $O P C$ we have
$$
O C \leq O P+P C=O B+O A=8
$$
Hence, the maximum yalue of the distance $O C$ is 8 (when the point $P$ lies on $O C$ )
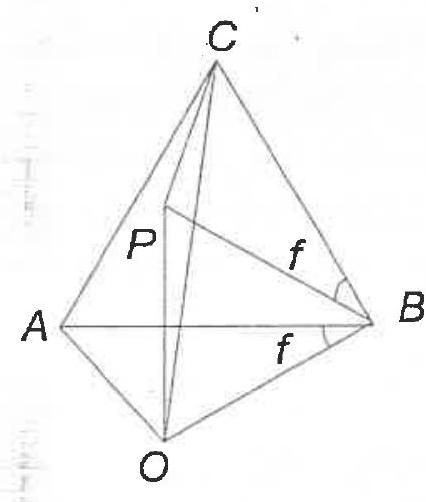
Figure 8
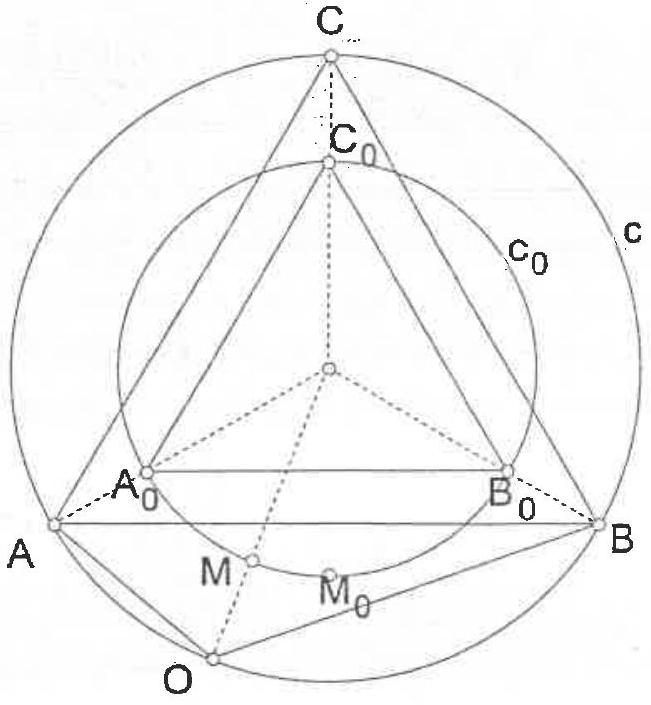
Figure 9
## Complement to the solution
Indeed there exists a triangle $\mathrm{OAB}$ with $\mathrm{OA}=3, \mathrm{OB}=5$ and $\mathrm{OC}=8$.
To construct such a triangle, let's first consider a point $M$ on the minor arc $\widehat{A_{0} B_{0}}$ of the circumference $\left(c_{0}\right)$ of an arbitrary equilateral triangle $A_{0} B_{0} C_{0}$. As $\mathrm{M}$ moves along $\widehat{\mathrm{A}_{0} \mathrm{~B}_{0}}$ from the midpoint position $\mathrm{M}_{0}$ towards $\mathrm{A}_{0}$, the ratio $\frac{\mathrm{MA}_{0}}{\mathrm{MB}_{0}}$ takes on all the decreasing values from 1 to 0 . Thus there exists a position of $\mathrm{M}$ such that $\frac{\mathrm{MA}_{0}}{\mathrm{MB}_{0}}=\frac{3}{5}$. Now a homothesy centered at the center of $\left(\mathrm{c}_{0}\right)$ can take $\mathrm{A}_{0}, \mathrm{~B}_{0}, \mathrm{C}_{0}, \mathrm{M}$ to the new positions $\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{O}$ so that $\mathrm{OA}=3$ and $\mathrm{OB}=5$. Then, since $\mathrm{C}$ lies on the minor arc $\overparen{\mathrm{AB}}$ of the circumference (c) of the equilateral triangle $\mathrm{ABC}$ we get $\mathrm{OC}=\mathrm{OA}+\mathrm{OB}=3+5=8$ as wanted, (figure 9).
| 8 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
NT1. Find all the natural numbers $m$ and $n$, such that the square of $m$ minus the product of $n$ with $k$, is 2 , where the number $k$ is obtained from $n$ by writing 1 on the left of the decimal notation of $n$.
| ## Solution
Let $t$ be the number of digits of $n$. Then $k=10^{t}+n$. So
$$
\mathrm{m}^{2}=n\left(10^{t}+\mathrm{n}\right)+2, \text { i.e. } \mathrm{m}^{2}-\mathrm{n}^{2}=10^{t} n+2
$$
This implies that $\mathrm{m}, \mathrm{n}$ are even and both $\mathrm{m}, \mathrm{n}$ are odd.
If $t=1$, then, 4 is divisor of $10 n+2$, so, $n$ is odd. We check that the only solution in this case is $\mathrm{m}=11$ and $\mathrm{n}=7$.
If $t>1$, then 4 is divisor of $\mathrm{m}^{2}-\mathrm{n}^{2}$, but 4 is not divisor of $10^{t}+2$.
Hence the only solution is $\mathrm{m}=11$ and $\mathrm{n}=7$.
| =11,n=7 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
NT2. Find all natural numbers $n$ such that $5^{n}+12^{n}$ is perfect square.
| ## Solution
By checking the cases $n=1,2,3$ we get the solution $n=2$ and $13^{2}=5^{2}+12^{2}$.
If $n=2 k+1$ is odd, we consider the equation modulo 5 and we obtain
$$
\begin{aligned}
x^{2} & \equiv 5^{2 k+1}+12^{2 k+1}(\bmod 5) \equiv 2^{2 k} \cdot 2(\bmod 5) \\
& \equiv(-1)^{k} \cdot 2(\bmod 5) \equiv \pm 2(\bmod 5)
\end{aligned}
$$
This is not possible, because the square residue of any natural number module 5 is 0,1 or 4. Therefore $n$ is even and $x^{2}=5^{2 k}+12^{2 k}$. Rearrange this equation in the form
$$
5^{2 k}=\left(x-12^{k}\right)\left(x+12^{k}\right)
$$
If 5 divides both factors on the right, it must also divide their difference, that is
$$
5 \mid\left(x+12^{k}\right)-\left(x-12^{k}\right)=2 \cdot 12^{k}
$$
which is not possible. Therefore we must have
$$
x-12^{k}=1 \text { and } x+12^{k}=5^{2 k}
$$
By adding the above equalities we get
$$
5^{2 k}-1=2 \cdot 12^{k}
$$
For $k \geq 2$, we have the inequality
$$
25^{k}-1>24^{k}=2^{k} \cdot 12^{k}>2 \cdot 12^{k}
$$
Thus we conclude that there exists a unique solution to our problem, namely $n=2$.
| 2 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
NT4. Find all the three digit numbers $\overline{a b c}$ such that
$$
\overline{a b c}=a b c(a+b+c)
$$
| ## Solution
We will show that the only solutions are 135 and 144 .
We have $a>0, b>0, c>0$ and
$$
9(11 a+b)=(a+b+c)(a b c-1)
$$
- If $a+b+c \equiv 0(\bmod 3)$ and $a b c-1 \equiv 0(\bmod 3)$, then $a \equiv b \equiv c \equiv 1(\bmod 3)$ and $11 a+b \equiv 0(\bmod 3)$. It follows now that
$$
a+b+c \equiv 0(\bmod 9) ; \text { or } a b c-1 \equiv 0(\bmod 9)
$$
- If . $a b c-1 \equiv 0(\bmod 9)$
we have $11 a+b=(a+b+c) k$, where $k$ is an integer
and is easy to see that we must have $19$.
Now we will deal with the case when $a+b+c \equiv 0(\bmod 9)$ or $a+b+c=9 l$, where $l$ is an integer.
- If $l \geq 2$ we have $a+b+c \geq 18, \max \{a, b, c\} \geq 6$ and it is easy to see that $a b c \geq 72$ and $a b c(a+b+c)>1000$,so the case $l \geq 2$ is impossible.
- If $l=1$ we have
$$
11 a+b=a b c-1 \text { or } 11 a+b+1=a b c \leq\left(\frac{a+b+c}{3}\right)^{3}=27
$$
So we have only two cases: $a=1$ or $a=2$.
- If $a=1$, we have $b+c=8$ and $11+b=b c-1$ or $b+(c-1)=7$ and $b(c-1)=12$ and the solutions are $(a, b, c)=(1,3,5)$ and $(a, b, c)=(1,4,4)$, and the answer is 135 and 144.
- If $a=2$ we have $b(2 c-1)=23$ and there is no solution for the problem.
| 135144 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
C4. Let $p_{1}, p_{2}, \ldots, p_{2005}$ be different prime numbers. Let $\mathrm{S}$ be a set of natural numbers which elements have the property that their simple divisors are some of the numbers $p_{1}, p_{2}, \ldots, p_{2005}$ and product of any two elements from $\mathrm{S}$ is not perfect square.
What is the maximum number of elements in $\mathrm{S}$ ?
| ## Solution
Let $a, b$ be two arbitrary numbers from $\mathrm{S}$. They can be written as
$$
a=p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{2005}^{a_{2005}} \text { and } b=p_{1}^{\beta_{1}} p_{2}^{\beta_{2}} \cdots p_{2005}^{\beta_{2005}}
$$
In order for the product of the elements $a$ and $b$ to be a square all the sums of the corresponding exponents need to be even from where we can conclude that for every $i, a_{i}$ and $\beta_{i}$ have the same parity. If we replace all exponents of $\mathrm{a}$ and $b$ by their remainders modulo 2 , then we get two numbers $a^{\prime}, b^{\prime}$ whose product is a perfect square if and only if ab is a perfect square.
In order for the product $a^{\prime} b^{\prime}$ not to be a perfect square, at least one pair of the corresponding exponents modulo 2, need to be of opposite parity.
Since we form 2005 such pairs modulo 2, and each number in these pairs is 1 or 2 , we conclude that we can obtain $2^{2005}$ distinct products none of which is a perfect square.
Now if we are given $2^{2005}+1$ numbers, thanks to Dirichlet's principle, there are at least two with the same sequence of modulo 2 exponents, thus giving a product equal to a square.
So, the maximal number of the elements of $S$ is $2^{2005}$.
| 2^{2005} | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
A4 Let $x, y$ be positive real numbers such that $x^{3}+y^{3} \leq x^{2}+y^{2}$. Find the greatest possible value of the product $x y$.
| ## Solution 1
We have $(x+y)\left(x^{2}+y^{2}\right) \geq(x+y)\left(x^{3}+y^{3}\right) \geq\left(x^{2}+y^{2}\right)^{2}$, hence $x+y \geq x^{2}+y^{2}$. Now $2(x+y) \geq(1+1)\left(x^{2}+y^{2}\right) \geq(x+y)^{2}$, thus $2 \geq x+y$. Because $x+y \geq 2 \sqrt{x y}$, we will obtain $1 \geq x y$. Equality holds when $x=y=1$.
So the greatest possible value of the product $x y$ is 1 .
| 1 | Inequalities | math-word-problem | Yes | Yes | olympiads | false |
A5 Determine the positive integers $a, b$ such that $a^{2} b^{2}+208=4\{l c m[a ; b]+g c d(a ; b)\}^{2}$.
| ## Solution
Let $d=\operatorname{gcd}(a, b)$ and $x, y \in \mathbb{Z}_{+}$such that $a=d x, b=d y$. Obviously, $(x, y)=1$. The equation is equivalent to $d^{4} x^{2} y^{2}+208=4 d^{2}(x y+1)^{2}$. Hence $d^{2} \mid 208$ or $d^{2} \mid 13 \cdot 4^{2}$, so $d \in\{1,2,4\}$. Take $t=x y$ with $t \in \mathbb{Z}_{+}$.
Case I. If $d=1$, then $(x y)^{2}+208=4(x y+1)^{2}$ or $3 t^{2}+8 t-204=0$, without solutions.
Case II. If $d=2$, then $16 x^{2} y^{2}+208=16(x y+1)^{2}$ or $t^{2}+13=t^{2}+2 t+1 \Rightarrow t=6$, so $(x, y) \in\{(1,6) ;(2,3) ;(3,2) ;(6,1)\} \Rightarrow(a, b) \in\{(2,12) ;(4,6) ;(6,4) ;(12 ; 2)\}$.
Case III. If $d=4$, then $16^{2} x^{2} y^{2}+208=4 \cdot 16(x y+1)^{2}$ or $16 t^{2}+13=4(t+1)^{2}$ and if $t \in \mathbb{Z}$, then 13 must be even, contradiction!
Finally, the solutions are $(a, b) \in\{(2,12) ;(4,6) ;(6,4) ;(12 ; 2)\}$.
| (,b)\in{(2,12);(4,6);(6,4);(12;2)} | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
A1 If for the real numbers $x, y, z, k$ the following conditions are valid, $x \neq y \neq z \neq x$ and $x^{3}+y^{3}+k\left(x^{2}+y^{2}\right)=y^{3}+z^{3}+k\left(y^{2}+z^{2}\right)=z^{3}+x^{3}+k\left(z^{2}+x^{2}\right)=2008$, find the product $x y z$.
|
Solution
$x^{3}+y^{3}+k\left(x^{2}+y^{2}\right)=y^{3}+z^{3}+k\left(y^{2}+z^{2}\right) \Rightarrow x^{2}+x z+z^{2}=-k(x+z):(1)$ and $y^{3}+z^{3}+k\left(y^{2}+z^{2}\right)=z^{3}+x^{3}+k\left(z^{2}+x^{2}\right) \Rightarrow y^{2}+y x+x^{2}=-k(y+x):(2)$
- From (1) $-(2) \Rightarrow x+y+z=-k:(*)$
- If $x+z=0$, then from $(1) \Rightarrow x^{2}+x z+z^{2}=0 \Rightarrow(x+z)^{2}=x z \Rightarrow x z=0$
So $x=z=0$, contradiction since $x \neq z$ and therefore $(1) \Rightarrow-k=\frac{x^{2}+x z+z^{2}}{x+z}$
Similarly we have: $-k=\frac{y^{2}+y x+x^{2}}{y+x}$.
So $\frac{x^{2}+x z+z^{2}}{x+z}=\frac{y^{2}+x y+x^{2}}{x+y}$ from which $x y+y z+z x=0:(* *)$.
We substitute $k$ in $x^{3}+y^{3}+k\left(x^{2}+y^{2}\right)=2008$ from the relation $(*)$ and using the $(* *)$, we finally obtain that $2 x y z=2008$ and therefore $x y z=1004$.
Remark: $x, y, z$ must be the distinct real solutions of the equation $t^{3}+k t^{2}-1004=0$. Such solutions exist if (and only if) $k>3 \sqrt[3]{251}$.
| xy1004 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
A2 Find all real numbers $a, b, c, d$ such that $a+b+c+d=20$ and $a b+a c+a d+b c+b d+c d=$ 150 .
| ## Solution
$400=(a+b+c+d)^{2}=a^{2}+b^{2}+c^{2}+d^{2}+2 \cdot 150$, so $a^{2}+b^{2}+c^{2}+d^{2}=100$. Now $(a-b)^{2}+(a-c)^{2}+(a-d)^{2}+(b-c)^{2}+(b-d)^{2}+(c-d)^{2}=3\left(a^{2}+b^{2}+c^{2}+d^{2}\right)-2(a b+$ $a c+a d+b c+b d+c d)=300-300=0$. Thus $a=b=c=d=5$.
| =b===5 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
A3 Let the real parameter $p$ be such that the system
$$
\left\{\begin{array}{l}
p\left(x^{2}-y^{2}\right)=\left(p^{2}-1\right) x y \\
|x-1|+|y|=1
\end{array}\right.
$$
has at least three different real solutions. Find $p$ and solve the system for that $p$.
| ## Solution
The second equation is invariant when $y$ is replaced by $-y$, so let us assume $y \geq 0$. It is also invariant when $x-1$ is replaced by $-(x-1)$, so let us assume $x \geq 1$. Under these conditions the equation becomes $x+y=2$, which defines a line on the coordinate plane. The set of points on it that satisfy the inequalities is a segment with endpoints $(1,1)$ and $(2,0)$. Now taking into account the invariance under the mentioned replacements, we conclude that the set of points satisfying the second equation is the square $\diamond$ with vertices $(1,1),(2,0),(1,-1)$ and $(0,0)$.
The first equation is equivalent to
$p x^{2}-p^{2} x y+x y-p y^{2}=0$
$p x(x-p y)+y(x-p y)=0$
$(p x+y)(x-p y)=0$.
Thus $y=-p x$ or $x=p y$. These are equations of two perpendicular lines passing through the origin, which is also a vertex of $\diamond$. If one of them passes through an interior point of the square, the other cannot have any common points with $\diamond$ other than $(0,0)$, so the system has two solutions. Since we have at least three different real solutions, the lines must contain some sides of $\diamond$, i.e. the slopes of the lines have to be 1 and -1 . This happens if $p=1$ or $p=-1$. In either case $x^{2}=y^{2},|x|=|y|$, so the second equation becomes $|1-x|+|x|=1$. It is true exactly when $0 \leq x \leq 1$ and $y= \pm x$.
| p=1orp=-1,0\leqx\leq1,withy=\x | Algebra | math-word-problem | Yes | Yes | olympiads | false |
A4 Find all triples $(x, y, z)$ of real numbers that satisfy the system
$$
\left\{\begin{array}{l}
x+y+z=2008 \\
x^{2}+y^{2}+z^{2}=6024^{2} \\
\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{2008}
\end{array}\right.
$$
| ## Solution
The last equation implies $x y z=2008(x y+y z+z x)$, therefore $x y z-2008(x y+y z+z x)+$ $2008^{2}(x+y+z)-2008^{3}=0$.
$(x-2008)(y-2008)(z-2008)=0$.
Thus one of the variable equals 2008. Let this be $x$. Then the first equation implies $y=-z$. From the second one it now follows that $2 y^{2}=6024^{2}-2008^{2}=2008^{2}(9-1)=$ $2 \cdot 4016^{2}$. Thus $(x, y, z)$ is the triple $(2008,4016,-4016)$ or any of its rearrangements.
| (2008,4016,-4016) | Algebra | math-word-problem | Yes | Yes | olympiads | false |
A5 Find all triples $(x, y, z)$ of real positive numbers, which satisfy the system
$$
\left\{\begin{array}{l}
\frac{1}{x}+\frac{4}{y}+\frac{9}{z}=3 \\
x+y+z \leq 12
\end{array}\right.
$$
| ## Solution
If we multiply the given equation and inequality $(x>0, y>0, z>0)$, we have
$$
\left(\frac{4 x}{y}+\frac{y}{x}\right)+\left(\frac{z}{x}+\frac{9 x}{z}\right)+\left(\frac{4 z}{y}+\frac{9 y}{z}\right) \leq 22
$$
From AM-GM we have
$$
\frac{4 x}{y}+\frac{y}{x} \geq 4, \quad \frac{z}{x}+\frac{9 x}{z} \geq 6, \quad \frac{4 z}{y}+\frac{9 y}{z} \geq 12
$$
Therefore
$$
22 \leq\left(\frac{4 x}{y}+\frac{y}{x}\right)+\left(\frac{z}{x}+\frac{9 x}{z}\right)+\left(\frac{4 z}{y}+\frac{9 y}{z}\right)
$$
Now from (1) and (3) we get
$$
\left(\frac{4 x}{y}+\frac{y}{x}\right)+\left(\frac{z}{x}+\frac{9 x}{z}\right)+\left(\frac{4 z}{y}+\frac{9 y}{z}\right)=22
$$
which means that in (2), everywhere equality holds i.e. we have equality between means, also $x+y+z=12$.
Therefore $\frac{4 x}{y}=\frac{y}{x}, \frac{z}{x}=\frac{9 x}{z}$ and, as $x>0, y>0, z>0$, we get $y=2 x, z=3 x$. Finally if we substitute for $y$ and $z$, in $x+y+z=12$, we get $x=2$, therefore $y=2 \cdot 2=4$ and $z=3 \cdot 2=6$.
Thus the unique solution is $(x, y, z)=(2,4,6)$.
| (2,4,6) | Algebra | math-word-problem | Yes | Yes | olympiads | false |
A9 Consider an integer $n \geq 4$ and a sequence of real numbers $x_{1}, x_{2}, x_{3}, \ldots, x_{n}$. An operation consists in eliminating all numbers not having the rank of the form $4 k+3$, thus leaving only the numbers $x_{3}, x_{7}, x_{11}, \ldots$ (for example, the sequence $4,5,9,3,6,6,1,8$ produces the sequence 9,1 . Upon the sequence $1,2,3, \ldots, 1024$ the operation is performed successively for 5 times. Show that at the end only 1 number remains and find this number.
| ## Solution
After the first operation 256 number remain; after the second one, 64 are left, then 16, next 4 and ultimately only one number.
Notice that the 256 numbers left after the first operation are $3,7, \ldots, 1023$, hence they are in arithmetical progression of common difference 4. Successively, the 64 numbers left after the second operation are in arithmetical progression of ratio 16 and so on.
Let $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$ be the first term in the 5 sequences obtained after each of the 5 operations. Thus $a_{1}=3$ and $a_{5}$ is the requested number. The sequence before the fifth operation has 4 numbers, namely
$$
a_{4}, a_{4}+256, a_{4}+512, a_{4}+768
$$
and $a_{5}=a_{4}+512$. Similarly, $a_{4}=a_{3}+128, a_{3}=a_{2}+32, a_{2}=a_{1}+8$.
Summing up yields $a_{5}=a_{1}+8+32+128+512=3+680=683$.
### 2.2 Combinatorics
| 683 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
G3 The vertices $A$ and $B$ of an equilateral $\triangle A B C$ lie on a circle $k$ of radius 1 , and the vertex $C$ is inside $k$. The point $D \neq B$ lies on $k, A D=A B$ and the line $D C$ intersects $k$ for the second time in point $E$. Find the length of the segment $C E$.
| ## Solution
As $A D=A C, \triangle C D A$ is isosceles. If $\varangle A D C=\varangle A C D=\alpha$ and $\varangle B C E=\beta$, then $\beta=120^{\circ}-\alpha$. The quadrilateral $A B E D$ is cyclic, so $\varangle A B E=180^{\circ}-\alpha$. Then $\varangle C B E=$ $120^{\circ}-\alpha$ so $\varangle C B E=\beta$. Thus $\triangle C B E$ is isosceles, so $A E$ is the perpendicular bisector of $B C$, so it bisects $\varangle B A C$. Now the arc $B E$ is intercepted by a $30^{\circ}$ inscribed angle, so it measures $60^{\circ}$. Then $B E$ equals the radius of $k$, namely 1 . Hence $C E=B E=1$.
| 1 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
G7 Let $A B C$ be an isosceles triangle with $A C=B C$. The point $D$ lies on the side $A B$ such that the semicircle with diameter $[B D]$ and center $O$ is tangent to the side $A C$ in the point $P$ and intersects the side $B C$ at the point $Q$. The radius $O P$ intersects the chord $D Q$ at the point $E$ such that $5 \cdot P E=3 \cdot D E$. Find the ratio $\frac{A B}{B C}$.
| ## Solution
We denote $O P=O D=O B=R, A C=B C=b$ and $A B=2 a$. Because $O P \perp A C$ and $D Q \perp B C$, then the right triangles $A P O$ and $B Q D$ are similar and $\varangle B D Q=\varangle A O P$. So, the triangle $D E O$ is isosceles with $D E=O E$. It follows that
$$
\frac{P E}{D E}=\frac{P E}{O E}=\frac{3}{5}
$$
Let $F$ and $G$ are the orthogonal projections of the points $E$ and $P$ respectively on the side $A B$ and $M$ is the midpoint of the side $[A B]$. The triangles $O F E, O G P, O P A$ and $C M A$ are similar. We obtain the following relations
$$
\frac{O F}{O E}=\frac{O G}{O P}=\frac{C M}{A C}=\frac{O P}{O A}
$$
But $C M=\sqrt{b^{2}-a^{2}}$ and we have $O G=\frac{R}{b} \cdot \sqrt{b^{2}-a^{2}}$. In isosceles triangle $D E O$ the point $F$ is the midpoint of the radius $D O$. So, $O F=R / 2$. By using Thales' theorem we obtain
$$
\frac{3}{5}=\frac{P E}{O E}=\frac{G F}{O F}=\frac{O G-O F}{O F}=\frac{O G}{O F}-1=2 \cdot \sqrt{1-\left(\frac{a}{b}\right)^{2}}-1
$$
From the last relations it is easy to obtain that $\frac{a}{b}=\frac{3}{5}$ and $\frac{A B}{B C}=\frac{6}{5}$.
The problem is solved.
| \frac{6}{5} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
NT1 Find all the positive integers $x$ and $y$ that satisfy the equation
$$
x(x-y)=8 y-7
$$
| ## Solution 1:
The given equation can be written as:
$$
\begin{aligned}
& x(x-y)=8 y-7 \\
& x^{2}+7=y(x+8)
\end{aligned}
$$
Let $x+8=m, m \in \mathbb{N}$. Then we have: $x^{2}+7 \equiv 0(\bmod m)$, and $x^{2}+8 x \equiv 0(\bmod m)$. So we obtain that $8 x-7 \equiv 0(\bmod m) \quad(1)$.
Also we obtain $8 x+8^{2}=8(x+8) \equiv 0(\bmod m) \quad(2)$.
From (1) and $(2)$ we obtain $(8 x+64)-(8 x-7)=71 \equiv 0(\bmod m)$, therefore $m \mid 71$, since 71 is a prime number, we have:
$x+8=1$ or $x+8=71$. The only accepted solution is $x=63$, and from the initial equation we obtain $y=56$.
Therefore the equation has a unique solution, namely $(x, y)=(63,56)$.
| (x,y)=(63,56) | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
NT3 Let $s(a)$ denote the sum of digits of a given positive integer $a$. The sequence $a_{1}, a_{2}, \ldots a_{n}, \ldots$ of positive integers is such that $a_{n+1}=a_{n}+s\left(a_{n}\right)$ for each positive integer $n$. Find the greatest possible $n$ for which it is possible to have $a_{n}=2008$.
| ## Solution
Since $a_{n-1} \equiv s\left(a_{n-1}\right)$ (all congruences are modulo 9 ), we have $2 a_{n-1} \equiv a_{n} \equiv 2008 \equiv 10$, so $a_{n-1} \equiv 5$. But $a_{n-1}<2008$, so $s\left(a_{n-1}\right) \leq 28$ and thus $s\left(a_{n-1}\right)$ can equal 5,14 or 23 . We check $s(2008-5)=s(2003)=5, s(2008-14)=s(1994)=23, s(2008-23)=s(1985)=$ 23. Thus $a_{n-1}$ can equal 1985 or 2003 . As above $2 a_{n-2} \equiv a_{n-1} \equiv 5 \equiv 14$, so $a_{n-2} \equiv 7$. But $a_{n-2}<2003$, so $s\left(a_{n-2}\right) \leq 28$ and thus $s\left(a_{n-2}\right)$ can equal 16 or 25 . Checking as above we see that the only possibility is $s(2003-25)=s(1978)=25$. Thus $a_{n-2}$ can be only 1978. Now $2 a_{n-3} \equiv a_{n-2} \equiv 7 \equiv 16$ and $a_{n-3} \equiv 8$. But $s\left(a_{n-3}\right) \leq 27$ and thus $s\left(a_{n-3}\right)$ can equal 17 or 26 . The check works only for $s(1978-17)=s(1961)=17$. Thus $a_{n-3}=1961$ and similarly $a_{n-4}=1939 \equiv 4, a_{n-5}=1919 \equiv 2$ (if they exist). The search for $a_{n-6}$ requires a residue of 1 . But $a_{n-6}<1919$, so $s\left(a_{n-6}\right) \leq 27$ and thus $s\left(a_{n-6}\right)$ can be equal only to 10 or 19 . The check fails for both $s(1919-10)=s(1909)=19$ and $s(1919-19)=s(1900)=10$. Thus $n \leq 6$ and the case $n=6$ is constructed above (1919, 1939, 1961, 1978, 2003, 2008).
| 6 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
NT4 Find all integers $n$ such that $n^{4}+8 n+11$ is a product of two or more consecutive integers.
|
Solution
We will prove that $n^{4}+8 n+11$ is never a multiple of 3 . This is clear if $n$ is a multiple of 3 . If
$n$ is not a multiple of 3 , then $n^{4}+8 n+11=\left(n^{4}-1\right)+12+8 n=(n-1)(n+1)\left(n^{2}+1\right)+12+8 n$, where $8 n$ is the only term not divisible by 3 . Thus $n^{4}+8 n+11$ is never the product of three or more integers.
It remains to discuss the case when $n^{4}+8 n+11=y(y+1)$ for some integer $y$. We write this as $4\left(n^{4}+8 n+11\right)=4 y(y+1)$ or $4 n^{4}+32 n+45=(2 y+1)^{2}$. A check shows that among $n= \pm 1$ and $n=0$ only $n=1$ satisfies the requirement, as $1^{4}+8 \cdot 1+11=20=4 \cdot 5$. Now let $|n| \geq 2$. The identities $4 n^{2}+32 n+45=\left(2 n^{2}-2\right)^{2}+8(n+2)^{2}+9$ and $4 n^{4}+32 n+45=$ $\left(2 n^{2}+8\right)^{2}-32 n(n-1)-19$ indicate that for $|n| \geq 2,2 n^{2}-2<2 y+1<2 n^{2}+8$. But $2 y+1$ is odd, so it can equal $2 n^{2} \pm 1 ; 2 n^{2}+3 ; 2 n^{2}+5$ or $2 n^{2}+7$. We investigate them one by one.
If $4 n^{4}+32 n+45=\left(2 n^{2}-1\right)^{2} \Rightarrow n^{2}+8 n+11=0 \Rightarrow(n+4)^{2}=5$, which is impossible, as 5 is not a perfect square.
If $4 n^{4}+32 n+45=\left(2 n^{2}+1\right)^{2} \Rightarrow n^{2}-8 n-11=0 \Rightarrow(n-4)^{2}=27$ which also fails.
Also $4 n^{4}+32 n+45=\left(2 n^{2}+3\right)^{2} \Rightarrow 3 n^{2}-8 n-9=0 \Rightarrow 9 n^{2}-24 n-27=0 \Rightarrow(3 n-4)^{2}=43$ fails.
If $4 n^{4}+32 n+45=\left(2 n^{2}+5\right)^{2} \Rightarrow 5 n^{2}-8 n=5 \Rightarrow 25 n^{2}-40 n=25 \Rightarrow(5 n-4)^{2}=41$ which also fails.
Finally, if $4 n^{4}+32 n+45=\left(2 n^{2}+7\right)^{2}$, then $28 n^{2}-32 n+4=0 \Rightarrow 4(n-1)(7 n-1)=0$, whence $n=1$ that we already found. Thus the only solution is $n=1$.
| 1 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
NT6 Let $f: \mathbb{N} \rightarrow \mathbb{R}$ be a function, satisfying the following condition:
for every integer $n>1$, there exists a prime divisor $p$ of $n$ such that $f(n)=f\left(\frac{n}{p}\right)-f(p)$. If
$$
f\left(2^{2007}\right)+f\left(3^{2008}\right)+f\left(5^{2009}\right)=2006
$$
determine the value of
$$
f\left(2007^{2}\right)+f\left(2008^{3}\right)+f\left(2009^{5}\right)
$$
| ## Solution
If $n=p$ is prime number, we have
$$
f(p)=f\left(\frac{p}{p}\right)-f(p)=f(1)-f(p)
$$
i.e.
$$
f(p)=\frac{f(1)}{2}
$$
If $n=p q$, where $p$ and $q$ are prime numbers, then
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=f(q)-f(p)=\frac{f(1)}{2}-\frac{f(1)}{2}=0
$$
If $n$ is a product of three prime numbers, we have
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=0-f(p)=-f(p)=-\frac{f(1)}{2}
$$
With mathematical induction by a number of prime multipliers we shell prove that: if $n$ is a product of $k$ prime numbers then
$$
f(n)=(2-k) \frac{f(1)}{2}
$$
For $k=1$, clearly the statement (2), holds.
Let statement (2) holds for all integers $n$, where $n$ is a product of $k$ prime numbers.
Now let $n$ be a product of $k+1$ prime numbers. Then we have $n=n_{1} p$, where $n_{1}$ is a product of $k$ prime numbers.
So
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=f\left(n_{1}\right)-f(p)=(2-k) \frac{f(1)}{2}-\frac{f(1)}{2}=(2-(k+1)) \frac{f(1)}{2}
$$
So (2) holds for every integer $n>1$.
Now from $f\left(2^{2007}\right)+f\left(3^{2008}\right)+f\left(5^{2009}\right)=2006$ and because of (2) we have
$$
\begin{aligned}
2006 & =f\left(2^{2007}\right)+f\left(3^{2008}\right)+f\left(5^{2009}\right) \\
& =\frac{2-2007}{2} f(1)+\frac{2-2008}{2} f(1)+\frac{2-2009}{2} f(1)=-\frac{3 \cdot 2006}{2} f(1)
\end{aligned}
$$
i.e.
$$
f(1)=-\frac{2}{3}
$$
Since
$$
2007=3^{2} \cdot 223,2008=2^{3} \cdot 251,2009=7^{2} \cdot 41
$$
and because of (2) and (3), we get
$$
\begin{aligned}
f\left(2007^{2}\right)+f\left(2008^{3}\right)+f\left(2009^{5}\right) & =\frac{2-6}{2} f(1)+\frac{2-12}{2} f(1)+\frac{2-15}{2} f(1) \\
& =-\frac{27}{2} f(1)=-\frac{27}{2} \cdot\left(-\frac{2}{3}\right)=9
\end{aligned}
$$
| 9 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
NT7 Determine the minimal prime number $p>3$ for which no natural number $n$ satisfies
$$
2^{n}+3^{n} \equiv 0(\bmod p)
$$
| ## Solution
We put $A(n)=2^{n}+3^{n}$. From Fermat's little theorem, we have $2^{p-1} \equiv 1(\bmod p)$ and $3^{p-1} \equiv 1(\bmod p)$ from which we conclude $A(n) \equiv 2(\bmod p)$. Therefore, after $p-1$ steps
at most, we will have repetition of the power. It means that in order to determine the minimal prime number $p$ we seek, it is enough to determine a complete set of remainders $S(p)=\{0,1, \ldots, p-1\}$ such that $2^{n}+3^{n} \not \equiv 0(\bmod p)$, for every $n \in S(p)$.
For $p=5$ and $n=1$ we have $A(1) \equiv 0(\bmod 5)$.
For $p=7$ and $n=3$ we have $A(3) \equiv 0(\bmod 7)$.
For $p=11$ and $n=5$ we have $A(5) \equiv 0(\bmod 11)$.
For $p=13$ and $n=2$ we have $A(2) \equiv 0(\bmod 13)$.
For $p=17$ and $n=8$ we have $A(8) \equiv 0(\bmod 17)$.
For $p=19$ we have $A(n) \not \equiv 0(\bmod 19)$, for all $n \in S(19)$.
Hence the minimal value of $p$ is 19 .
| 19 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
NT8 Let $a, b, c, d, e, f$ are nonzero digits such that the natural numbers $\overline{a b c}, \overline{d e f}$ and $\overline{a b c d e f}$ are squares.
a) Prove that $\overline{a b c d e f}$ can be represented in two different ways as a sum of three squares of natural numbers.
b) Give an example of such a number.
|
Solution
a) Let $\overline{a b c}=m^{2}, \overline{d e f}=n^{2}$ and $\overline{a b c d e f}=p^{2}$, where $11 \leq m \leq 31,11 \leq n \leq 31$ are natural numbers. So, $p^{2}=1000 \cdot m^{2}+n^{2}$. But $1000=30^{2}+10^{2}=18^{2}+26^{2}$. We obtain the following relations
$$
\begin{gathered}
p^{2}=\left(30^{2}+10^{2}\right) \cdot m^{2}+n^{2}=\left(18^{2}+26^{2}\right) \cdot m^{2}+n^{2}= \\
=(30 m)^{2}+(10 m)^{2}+n^{2}=(18 m)^{2}+(26 m)^{2}+n^{2}
\end{gathered}
$$
The assertion a) is proved.
b) We write the equality $p^{2}=1000 \cdot m^{2}+n^{2}$ in the equivalent form $(p+n)(p-n)=1000 \cdot m^{2}$, where $349 \leq p \leq 979$. If $1000 \cdot m^{2}=p_{1} \cdot p_{2}$, such that $p+n=p_{1}$ and $p-n=p_{2}$, then $p_{1}$ and $p_{2}$ are even natural numbers with $p_{1}>p_{2} \geq 318$ and $22 \leq p_{1}-p_{2} \leq 62$. For $m=15$ we obtain $p_{1}=500, p_{2}=450$. So, $n=25$ and $p=475$. We have
$$
225625=475^{2}=450^{2}+150^{2}+25^{2}=270^{2}+390^{2}+25^{2}
$$
The problem is solved.
| 225625=475^{2}=450^{2}+150^{2}+25^{2}=270^{2}+390^{2}+25^{2} | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
NT9 Let $p$ be a prime number. Find all positive integers $a$ and $b$ such that:
$$
\frac{4 a+p}{b}+\frac{4 b+p}{a}
$$
and
$$
\frac{a^{2}}{b}+\frac{b^{2}}{a}
$$
are integers.
| ## Solution
Since $a$ and $b$ are symmetric we can assume that $a \leq b$. Let $d=(a, b), a=d u, b=d v$ and $(u, v)=1$. Then we have:
$$
\frac{a^{2}}{b}+\frac{b^{2}}{a}=\frac{d\left(u^{3}+v^{3}\right)}{u v}
$$
Since,
$$
\left(u^{3}+v^{3}, u\right)=\left(u^{3}+v^{3}, v\right)=1
$$
we deduce that $u \mid d$ and $v \mid d$. But as $(u, v)=1$, it follows that $u v \mid d$.
Now, let $d=u v t$. Furthermore,
$$
\frac{4 a+p}{b}+\frac{4 b+p}{a}=\frac{4\left(a^{2}+b^{2}\right)+p(a+b)}{a b}=\frac{4 u v t\left(u^{2}+v^{2}\right)+p(u+v)}{u^{2} v^{2} t}
$$
This implies,
$$
u v \mid p(u+v)
$$
But from our assumption $1=(u, v)=(u, u+v)=(v, u+v)$ we conclude $u v \mid p$. Therefore, we have three cases $\{u=v=1\},\{u=1, v=p\},\{u=p, v=1\}$. We assumed that $a \leq b$, and this implies $u \leq v$.
If $a=b$, we need $\frac{4 a+p}{a}+\frac{4 a+p}{a} \in \mathbb{N}$, i.e. $a \mid 2 p$. Then $a \in\{1,2, p, 2 p\}$. The other condition being fulfilled, we obtain the solutions $(1,1),(2,2),(p, p)$ and $(2 p, 2 p)$.
Now, we have only one case to investigate, $u=1, v=p$. The last equation is transformed into:
$$
\frac{4 a+p}{b}+\frac{4 b+p}{a}=\frac{4 p t\left(1+p^{2}\right)+p(p+1)}{p^{2} t}=\frac{4 t+1+p(1+4 p t)}{p t}
$$
From the last equation we derive
$$
p \mid(4 t+1)
$$
Let $4 t+1=p q$. From here we derive
$$
\frac{4 t+1+p(1+4 p t)}{p t}=\frac{q+1+4 p t}{t}
$$
Now, we have
$$
t \mid(q+1)
$$
or
$$
q+1=\text { st. }
$$
Therefore,
$$
p=\frac{4 t+1}{q}=\frac{4 t+1}{s t-1}
$$
Since $p$ is a prime number, we deduce
$$
\frac{4 t+1}{s t-1} \geq 2
$$
or
$$
s \leq \frac{4 t+3}{2 t}=2+\frac{3}{2 t}<4
$$
Case 1: $s=1, p=\frac{4 t+1}{t-1}=4+\frac{5}{t-1}$. We conclude $t=2$ or $t=6$. But when $t=2$, we have $p=9$, not a prime. When $t=6, p=5, a=30, b=150$.
Case 2: $s=2, p=\frac{4 t+1}{2 t-1}=2+\frac{3}{2 t-1}$. We conclude $t=1, p=5, a=5, b=25$ or $t=2, p=3, a=6, b=18$.
Case 3: $s=3, p=\frac{4 t+1}{3 t-1}$ or $3 p=4+\frac{7}{3 t-1}$. As 7 does not have any divisors of the form $3 t-1$, in this case we have no solutions.
So, the solutions are
$$
(a, b)=\{(1,1),(2,2),(p, p),(2 p, 2 p),(5,25),(6,18),(18,6),(25,5),(30,150),(150,30)\}
$$
| (,b)={(1,1),(2,2),(p,p),(2p,2p),(5,25),(6,18),(18,6),(25,5),(30,150),(150,30)} | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
NT11 Determine the greatest number with $n$ digits in the decimal representation which is divisible by 429 and has the sum of all digits less than or equal to 11 .
| ## Solution
Let $A=\overline{a_{n} a_{n-1} \ldots a_{1}}$ and notice that $429=3 \cdot 11 \cdot 13$.
Since the sum of the digits $\sum a_{i} \leq 11$ and $\sum a_{i}$ is divisible by 3 , we get $\sum a_{i}=3,6$ or 9. As 11 divides $A$, we have
$$
11 \mid a_{n}-a_{n-1}+a_{n-2}-a_{n-3}+\ldots
$$
in other words $11 \mid \sum_{i \text { odd }} a_{i}-\sum_{i \text { even }} a_{i}$. But
$$
-9 \leq-\sum a_{i} \leq \sum_{i \text { odd }} a_{i}-\sum_{i \text { even }} a_{i} \leq \sum a_{i} \leq 9
$$
so $\sum_{i \text { odd }} a_{i}-\sum_{i \text { even }} a_{i}=0$. It follows that $\sum a_{i}$ is even, so $\sum a_{i}=6$ and $\sum_{i \text { odd }} a_{i}=\sum_{i \text { even }} a_{i}=3$.
The number 13 is a divisor of 1001 , hence
$$
13 \mid \overline{a_{3} a_{2} a_{1}}-\overline{a_{6} a_{5} a_{4}}+\overline{a_{9} a_{8} a_{7}}-\overline{a_{12} a_{11} a_{10}}+\ldots
$$
For each $k=1,2,3,4,5,6$, let $s_{k}$ be the sum of the digits $a_{k+6 m}, m \geq 0$; that is
$$
s_{1}=a_{1}+a_{7}+a_{13}+\ldots \text { and so on. }
$$
With this notation, (1) rewrites as
$$
13 \mid 100\left(s_{3}-s_{6}\right)+10\left(s_{2}-s_{5}\right)+\left(s_{1}-s_{4}\right), \text { or } 13 \mid 4\left(s_{6}-s_{3}\right)+3\left(s_{5}-s_{2}\right)+\left(s_{1}-s_{4}\right)
$$
Let $S_{3}=s_{3}-s_{6}, S_{2}=s_{2}-s_{5}$, and $S_{1}=s_{1}-s_{4}$. Recall that $\sum_{i \text { odd }} a_{i}=\sum_{i \text { even }} a_{i}$, which implies $S_{2}=S_{1}+S_{3}$. Then
$$
13\left|4 S_{3}+3 S_{2}-S_{1}=7 S_{3}+2 S_{1} \Rightarrow 13\right| 49 S_{3}+14 S_{1} \Rightarrow 13 \mid S_{1}-3 S_{3}
$$
Observe that $\left|S_{1}\right| \leq s_{1}=\sum_{i \text { odd }} a_{i}=3$ and likewise $\left|S_{2}\right|,\left|S_{3}\right| \leq 3$. Then $-13<S_{1}-3 S_{3}<13$ and consequently $S_{1}=3 S_{3}$. Thus $S_{2}=4 S_{3}$ and $\left|S_{2}\right| \leq 3$ yields $S_{2}=0$ and then $S_{1}=S_{3}=0$. We have $s_{1}=s_{4}, s_{2}=s_{5}, s_{3}=s_{6}$ and $s_{1}+s_{2}+s_{3}=3$, so the greatest number $A$ is $30030000 \ldots$.
| 30030000\ldots | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
NT12 Solve the equation $\frac{p}{q}-\frac{4}{r+1}=1$ in prime numbers.
| ## Solution
We can rewrite the equation in the form
$$
\begin{gathered}
\frac{p r+p-4 q}{q(r+1)}=1 \Rightarrow p r+p-4 q=q r+q \\
p r-q r=5 q-p \Rightarrow r(p-q)=5 q-p
\end{gathered}
$$
It follows that $p \neq q$ and
$$
\begin{gathered}
r=\frac{5 q-p}{p-q}=\frac{4 q+q-p}{p-q} \\
r=\frac{4 q}{p-q}-1
\end{gathered}
$$
As $p$ is prime, $p-q \neq q, p-q \neq 2 q, p-q \neq 4 q$.
We have $p-q=1$ or $p-q=2$ or $p-q=4$
i) If $p-q=1$ then
$$
q=2, p=3, r=7
$$
ii) If $p-q=2$ then $p=q+2, r=2 q-1$
If $q=1(\bmod 3)$ then $q+2 \equiv 0(\bmod 3)$
$$
q+2=3 \Rightarrow q=1
$$
contradiction.
If $q \equiv-1(\bmod 3)$ then $r \equiv-2-1 \equiv 0(\bmod 3)$
$$
\begin{gathered}
r=3 \\
r=2 q-1=3 \\
q=2 \\
p=4
\end{gathered}
$$
contradiction.
Hence $q=3, p=5, r=5$.
iii) If $p-q=4$ then $p=q+4$.
$r=q-1$
Hence $q=3, p=7, r=2$.
| (p,q,r)=(3,2,7), | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
COM 2 Natural numbers 1,2,3, .., 2003 are written in an arbitrary sequence $a_{1}, a_{2}, a_{3}, \ldots a_{2003}$. Let $b_{1}=1 a_{1}, b_{2}=2 a_{2}, b_{3}=3 a_{3}, \ldots, b_{2003}=2003 a_{2003}$, and $B$ be the maximum of the numbers $b_{1}, b_{2}, b_{3}, \ldots, b_{2003}$.
a) If $a_{1}=2003, a_{2}=2002, a_{3}=2001, \ldots, a_{2002}=2, a_{2003}=1$, find the value of $B$.
b) Prove that $B \geq 1002^{2}$.
|
Solution: a) Using the inequality between the arithmetical and geometrical mean, we obtain that $b_{n}=n(2004-n) \leq\left(\frac{n+(2004-n)}{2}\right)^{2}=1002^{2}$ for $n=1,2,3, \ldots, 2003$. The equality holds if and only if $n=2004-n$, i.e. $n=1002$. Therefore, $B=b_{1002}=1002 \times(2004-1002)=1002^{2}$. b) Let $a_{1}, a_{2}, a_{3}, \ldots a_{2003}$ be an arbitrary order of the numbers $1,2,3, \ldots, 2003$. First, we will show that numbers $1002,1003,1004, \ldots, 2003$ cannot occulpy the places numbered $1,2,3$, $\ldots, 1001$ only. Indeed, we have $(2003-1002)+1=1002$ numbers and 1002 places. This means that at least one of the numbers $1002,1003,1004, \ldots, 2003$, say $a_{m}$, lies on a place which number $m$ is greater than 1001 . Therefore, $B \geq m a \geq 1002 \times 1002=1002^{2}$.
| 1002^2 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
87.3. Let $f$ be a strictly increasing function defined in the set of natural numbers satisfying the conditions $f(2)=a>2$ and $f(m n)=f(m) f(n)$ for all natural numbers $m$ and $n$. Determine the smallest possible value of $a$.
|
Solution. Since $f(n)=n^{2}$ is a function satisfying the conditions of the problem, the smallest posiible $a$ is at most 4. Assume $a=3$. It is easy to prove by induction that $f\left(n^{k}\right)=f(n)^{k}$ for all $k \geq 1$. So, taking into account that $f$ is strictly increasing, we get
$$
\begin{gathered}
f(3)^{4}=f\left(3^{4}\right)=f(81)>f(64)=f\left(2^{6}\right)=f(2)^{6} \\
=3^{6}=27^{2}>25^{2}=5^{4}
\end{gathered}
$$
as well as
$$
\begin{aligned}
& f(3)^{8}=f\left(3^{8}\right)=f(6561)<f(8192) \\
& \quad=f\left(2^{13}\right)=f(2)^{13}=3^{13}<6^{8}
\end{aligned}
$$
So we arrive at $5<f(3)<6$. But this is not possible, since $f(3)$ is an integer. So $a=4$.
| 4 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
88.1. The positive integer $n$ has the following property: if the three last digits of $n$ are removed, the number $\sqrt[3]{n}$ remains. Find $n$.
|
Solution. If $x=\sqrt[3]{n}$, and $y, 0 \leq y1000$, and $x>31$. On the other hand, $x^{3}<1000 x+1000$, or $x\left(x^{2}-1000\right)<1000$. The left hand side of this inequality is an increasing function of $x$, and $x=33$ does not satisfy the inequality. So $x<33$. Since $x$ is an integer, $x=32$ and $n=32^{3}=32768$.
| 32768 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
89.2. Three sides of a tetrahedron are right-angled triangles having the right angle at their common vertex. The areas of these sides are $A, B$, and $C$. Find the total surface area of the tetrahedron.
|
Solution 1. Let $P Q R S$ be the tetrahedron of the problem and let $S$ be the vertex common to the three sides which are right-angled triangles. Let the areas of $P Q S, Q R S$, and $R P S$ be $A, B$, and $C$, respectively. Denote the area of $Q R S$ by $X$. If $S S^{\prime}$ is the altitude from $S$ (onto $P Q R$ ) and $\angle R S S^{\prime}=\alpha, \angle P S S^{\prime}=\beta, \angle Q S S^{\prime}=\gamma$, the rectangular parallelepiped with $S S^{\prime}$ as a diameter, gives by double use of the Pythagorean theorem
$$
\begin{gathered}
S S^{\prime 2}=\left(S S^{\prime} \cos \alpha\right)^{2}+\left(S S^{\prime} \sin \alpha\right)^{2} \\
=\left(S S^{\prime} \cos \alpha\right)^{2}+\left(S S^{\prime} \cos \beta\right)^{2}+\left(S S^{\prime} \cos \gamma\right)^{2}
\end{gathered}
$$
or
$$
\cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma=1
$$
(a well-known formula). The magnitude of the dihedral angle between two planes equals the angle between the normals of the planes. So $\alpha, \beta$, and $\gamma$ are the magnitudes of the dihedral angles between $P Q R$ and $P Q S, Q R S$, and $R P S$, respectively. Looking at the projections of $P Q R$ onto the three other sides of $P Q R S$, we get $A=X \cos \alpha, B=X \cos \beta$, and $C=X \cos \gamma$. But (1) now yields $X^{2}=A^{2}+B^{2}+C^{2}$. The total area of $P Q R S$ then equals $A+B+C+\sqrt{A^{2}+B^{2}+C^{2}}$.
| A+B+C+\sqrt{A^{2}+B^{2}+C^{2}} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
91.1. Determine the last two digits of the number
$$
2^{5}+2^{5^{2}}+2^{5^{3}}+\cdots+2^{5^{1991}}
$$
written in decimal notation.
|
Solution. We first show that all numbers $2^{5^{k}}$ are of the form $100 p+32$. This can be shown by induction. The case $k=1$ is clear $\left(2^{5}=32\right)$. Assume $2^{5^{k}}=100 p+32$. Then, by the binomial formula,
$$
2^{5^{k+1}}=\left(2^{5^{k}}\right)^{5}=(100 p+32)^{5}=100 q+32^{5}
$$
and
$$
\begin{gathered}
(30+2)^{5}=30^{5}+5 \cdot 30^{4} \cdot 2+10 \cdot 30^{3} \cdot 4+10 \cdot 30^{2} \cdot 8+5 \cdot 30 \cdot 16+32 \\
=100 r+32
\end{gathered}
$$
So the last two digits of the sum in the problem are the same as the last digits of the number $1991 \cdot 32$, or 12 .
| 12 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
92.1. Determine all real numbers $x>1, y>1$, and $z>1$, satisfying the equation
$$
\begin{aligned}
x+y+z+\frac{3}{x-1} & +\frac{3}{y-1}+\frac{3}{z-1} \\
& =2(\sqrt{x+2}+\sqrt{y+2}+\sqrt{z+2})
\end{aligned}
$$
|
Solution. Consider the function $f$,
$$
f(t)=t+\frac{3}{t-1}-2 \sqrt{t+2}
$$
defined for $t>1$. The equation of the problem can be written as
$$
f(x)+f(y)+f(z)=0
$$
We reformulate the formula for $f$ :
$$
\begin{aligned}
f(t) & =\frac{1}{t-1}\left(t^{2}-t+3-2(t-1) \sqrt{t+2}\right) \\
& =\frac{1}{t-1}\left(t^{2}-2 t+1+(\sqrt{t+2})^{2}-2(t-1) \sqrt{t+2}\right) \\
& =\frac{1}{t-1}(t-1-\sqrt{t+2})^{2}
\end{aligned}
$$
So $f(t) \geq 0$, and $f(t)=0$ for $t>1$ only if
$$
t-1=\sqrt{t+2}
$$
or
$$
t^{2}-3 t-1=0
$$
The only $t$ satisfying this condition is
$$
t=\frac{3+\sqrt{13}}{2}
$$
So the only solution to the equation in the problem is given by
$$
x=y=z=\frac{3+\sqrt{13}}{2}
$$
| \frac{3+\sqrt{13}}{2} | Algebra | math-word-problem | Yes | Yes | olympiads | false |
92.4. Peter has many squares of equal side. Some of the squares are black, some are white. Peter wants to assemble a big square, with side equal to $n$ sides of the small squares, so that the big square has no rectangle formed by the small squares such that all the squares in the vertices of the rectangle are of equal colour. How big a square is Peter able to assemble?
|
Solution. We show that Peter only can make a $4 \times 4$ square. The construction is possible, if $n=4$ :

Now consider the case $n=5$. We may assume that at least 13 of the 25 squares are black. If five black squares are on one horizontal row, the remaining eight ones are distributed on the other four rows. At least one row has two black squres. A rectangle with all corners black is created. Next assume that one row has four black squares. Of the remaing 9 squares, at least three are one row. At least two of these three have to be columns having the assumed four black squares. If no row has more than four black squares, there have to be at least three rows with exactly three black squares. Denote these rows by $A, B$, and $C$. Let us call the columns in which the black squares on row $A$ lie black columns, and the other two columns white columns. If either row $B$ or row $C$ has at least two black squares which are on black columns, a rectancle with black corners arises. If both rows $B$ and $C$ have only one black square on the black columns, then both of them have two black squares on the two white columns, and they make the black corners of a rectangle. So Peter cannot make a $5 \times 5$ square in the way he wishes.
| 4 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
93.1. Let $F$ be an increasing real function defined for all $x, 0 \leq x \leq 1$, satisfying the conditions
$$
\begin{aligned}
& F\left(\frac{x}{3}\right)=\frac{F(x)}{2} \\
& F(1-x)=1-F(x)
\end{aligned}
$$
Determine $F\left(\frac{173}{1993}\right)$ and $F\left(\frac{1}{13}\right)$.
|
Solution. Condition (i) implies $F(0)=\frac{1}{2} F(0)$, so $F(0)=0$. Because of condition (ii), $F(1)=1-F(0)=1$. Also $F\left(\frac{1}{3}\right)=\frac{1}{2}$ and $F\left(\frac{2}{3}\right)=1-F\left(\frac{1}{3}\right)=\frac{1}{2}$. Since $F$ is an increasing function, this is possible only if $F(x)=\frac{1}{2}$ for all $x \in\left[\frac{1}{3}, \frac{2}{3}\right]$. To determine the first of the required values of $F$, we use (i) and (ii) to transform the argument into the middle third of $[0,1]$ :
$$
F\left(\frac{173}{1993}\right)=\frac{1}{2} F\left(\frac{519}{1993}\right)=\frac{1}{4} F\left(\frac{1557}{1993}\right)
$$
$$
\begin{gathered}
=\frac{1}{4}\left(1-F\left(\frac{436}{1993}\right)\right)=\frac{1}{4}\left(1-\frac{1}{2} F\left(\frac{1308}{1993}\right)\right) \\
=\frac{1}{4}\left(1-\frac{1}{4}\right)=\frac{3}{16}
\end{gathered}
$$
To find the second value of $F$, we use (i) and (ii) to form an equation fron which the value can be solved. Indeed,
$$
\begin{gathered}
F\left(\frac{1}{13}\right)=1-F\left(\frac{12}{13}\right)=1-2 F\left(\frac{4}{13}\right) \\
=1-2\left(1-F\left(\frac{9}{13}\right)\right)=2 F\left(\frac{9}{13}\right)-1=4 F\left(\frac{3}{13}\right)-1 \\
=8 F\left(\frac{1}{13}\right)-1
\end{gathered}
$$
From this we solve
$$
F\left(\frac{1}{13}\right)=\frac{1}{7}
$$
| \frac{3}{16},\frac{1}{7} | Algebra | math-word-problem | Yes | Yes | olympiads | false |
93.3. Find all solutions of the system of equations
$$
\left\{\begin{aligned}
s(x)+s(y) & =x \\
x+y+s(z) & =z \\
s(x)+s(y)+s(z) & =y-4
\end{aligned}\right.
$$
where $x, y$, and $z$ are positive integers, and $s(x), s(y)$, and $s(z)$ are the numbers of digits in the decimal representations of $x, y$, and $z$, respectively.
|
Solution. The first equation implies $x \geq 2$ and the first and third equation together imply
$$
s(z)=y-x-4
$$
So $y \geq x+5 \geq 7$. From (1) and the second equation we obtain $z=2 y-4$. Translated to the values of $s$, these equation imply $s(x) \leq s(2 y) \leq s(y)+1$ and $s(x) \leq s(y)$. We insert these inequalitien in the last equation of the problem to obtain $y-4 \leq 3 s(y)+1$ or $y \leq 3 s(y)+5$. Since $10^{s(y)-1} \leq y$, the only possible values of $s(y)$ are 1 and 2 . If $s(y)=1$, then $7 \leq y \leq 3+5=8$. If $y=7, x$ must be 2 and $z=2 \cdot 7-4=10$. But this does not fit in the second equation: $2+7+2 \neq 10$. If $y=8$, then $z=12, x=2$. The triple $(2,8,12)$ satisfies all the equations of the problem. If $s(y)=2$, then $y \leq 6+5=11$. The only possibilities are $y=10$ and $y=11$. If $y=10$, then $z=16$ and $x \leq 5$. The equation $s(x)+s(y)+s(z)=y-4=6$ is not satisfied. If $y=11$, then $z=18$ and $x \leq 6$. Again, the third equation is not satisfied. So $x=2, y=8$, and $z=12$ is the only solution.
| (2,8,12) | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
94.4. Determine all positive integers $n<200$, such that $n^{2}+(n+1)^{2}$ is the square of an integer.
|
Solution. We determine the integral solutions of
$$
n^{2}+(n+1)^{2}=(n+p)^{2}, \quad p \geq 2
$$
The root formula for quadratic equations yields
$$
n=p-1+\sqrt{2 p(p-1)} \geq 2(p-1)
$$
Because $n<200$, we have $p \leq 100$. Moreover, the number $2 p(p-1)$ has to be the square of an integer. If $p$ is odd, $p$ and $2(p-1)$ have no common factors. Consequently, both $p$ and $2(p-1)$ have to be squares. The only possible candidates are $p=9, p=25, p=49$, $p=81$. The respective numbers $2(p-1)$ are $16,48,96$, and 160 . Of these, only 16 is a square. We thus have one solution $n=8+\sqrt{2 \cdot 9 \cdot 8}=20,20^{2}+21^{2}=841=29^{2}$. If $p$ is even, the numbers $2 p$ and $p-1$ have no factors in common, so both are squares. Possible candidates for $2 p$ are $4,16,36,64,100,144$, and 196. The corresponding values of $p-1$ are $1,7,31,49,71,97$. We obtain two more solutions: $n=1+2=3,3^{2}+4^{2}=5^{2}$, and $n=49+70=119,119^{2}+120^{2}=169^{2}$.
| 20,3,119 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
95.2. Messages are coded using sequences consisting of zeroes and ones only. Only sequences with at most two consecutive ones or zeroes are allowed. (For instance the sequence 011001 is allowed, but 011101 is not.) Determine the number of sequences consisting of exactly 12 numbers.
|
Solution 1. Let $S_{n}$ be the set of acceptable sequences consisting of $2 n$ digits. We partition $S_{n}$ in subsets $A_{n}, B_{n}, C_{n}$, and $D_{n}$, on the basis of the two last digits of the sequence. Sequences ending in 00 are in $A_{n}$, those ending in 01 are in $B_{n}$, those ending in 10 are in $C_{n}$, and those ending in 11 are in $D_{n}$. Denote by $x_{n}, a_{n}, b_{n}, c_{n}$, and $d_{n}$ the number of elements in $S_{n}, A_{n}, B_{n}, C_{n}$, and $D_{n}$. We compute $x_{6}$. Because $S_{1}=\{00,01,10,11\}$, $x_{1}=4$ and $a_{1}=b_{1}=c_{1}=d_{1}=1$. Every element of $A_{n+1}$ can be obtained in a unique manner from an element of $B_{n}$ or $D_{n}$ by adjoining 00 to the end. So $a_{n+1}=b_{n}+d_{n}$. The elements of $B_{n+1}$ are similarly obtained from elements of $B_{n}, C_{n}$, and $D_{n}$ by adjoining 01 to the end. So $b_{n+1}=b_{n}+c_{n}+d_{n}$. In a similar manner we obtain the recursion formulas $c_{n+1}=a_{n}+b_{n}+c_{n}$ and $d_{n+1}=a_{n}+c_{n}$. So $a_{n+1}+d_{n+1}=\left(b_{n}+d_{n}\right)+\left(a_{n}+c_{n}\right)=x_{n}$ and $x_{n+1}=2 a_{n}+3 b_{n}+3 c_{n}+2 d_{n}=3 x_{n}-\left(a_{n}+b_{n}\right)=3 x_{n}-x_{n-1}$. Starting from the initial values $a_{1}=b_{1}=c_{1}=d_{1}=1$, we obtain $a_{2}=d_{2}=2, b_{2}=c_{2}=3$, and $x_{2}=10$. So $x_{3}=3 x_{2}-x_{1}=3 \cdot 10-4=26, x_{4}=3 \cdot 26-10=68, x_{5}=3 \cdot 68-26=178$, and $x_{6}=3 \cdot 178-68=466$.
| 466 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
96.2. Determine all real numbers $x$, such that
$$
x^{n}+x^{-n}
$$
is an integer for all integers $n$.
|
Solution. Set $f_{n}(x)=x^{n}+x^{-n}$. $f_{n}(0)$ is not defined for any $n$, so we must have $x \neq 0$. Since $f_{0}(x)=2$ for all $x \neq 0$, we have to find out those $x \neq 0$ for which $f_{n}(x)$ is an integer foe every $n>0$. We note that
$$
x^{n}+x^{-n}=\left(x+x^{-1}\right)\left(x^{n-1}+x^{1-n}\right)-\left(x^{n-2}+x^{2-n}\right)
$$
From this we obtain by induction that $x^{n}+x^{-n}$ is an integer for all $n>1$ as soon as $x+x^{-1}$ is an integer. So $x$ has to satisfy
$$
x+x^{-1}=m
$$
where $m$ is an integer. The roots of this quadratic equation are
$$
x=\frac{m}{2} \pm \sqrt{\frac{m^{2}}{4}-1}
$$
and they are real, if $m \neq-1,0,1$.
| \frac{}{2}\ | Algebra | math-word-problem | Yes | Yes | olympiads | false |
97.1. Let A be a set of seven positive numbers. Determine the maximal number of triples $(x, y, z)$ of elements of A satisfying $x<y$ and $x+y=z$.
|
Solution. Let $0<a_{1}<a_{2}<\ldots<a_{7}$ be the elements of the set $A$. If $\left(a_{i}, a_{j}, a_{k}\right)$ is a triple of the kind required in the problem, then $a_{i}<a_{j}<a_{i}+a_{j}=a_{k}$. There are at most $k-1$ pairs $\left(a_{i}, a_{j}\right)$ such that $a_{i}+a_{j}=a_{k}$. The number of pairs satisfying $a_{i}<a_{j}$ is at most $\left\lfloor\frac{k-1}{2}\right\rfloor$. The total number of pairs is at most
$$
\sum_{k=3}^{7}\left\lfloor\frac{k-1}{2}\right\rfloor=1+1+2+2+3=9
$$
The value 9 can be reached, if $A=\{1,2, \ldots, 7\}$. In this case the triples $(1,2,3),(1,3,4)$, $(1,4,5),(1,5,6),(1,6,7),(2,3,5),(2,4,6),(2,5,7)$, and $(3,4,7)$ satisfy the conditions of the problem.
| 9 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
97.3. Let $A, B, C$, and $D$ be four different points in the plane. Three of the line segments $A B, A C, A D, B C, B D$, and $C D$ have length a. The other three have length $b$, where $b>a$. Determine all possible values of the quotient $\frac{b}{a}$.
|
Solution. If the three segments of length $a$ share a common endpoint, say $A$, then the other three points are on a circle of radius $a$, centered at $A$, and they are the vertices of an equilateral triangle of side length $b$. But this means that $A$ is the center of the triangle $B C D$, and
$$
\frac{b}{a}=\frac{b}{\frac{2}{3} \frac{\sqrt{3}}{2} b}=\sqrt{3}
$$
Assume then that of the segments emanating from $A$ at least one has lenght $a$ and at least one has length $b$. We may assume $A B=a$ and $A D=b$. If only one segment of length $a$ would emanate from each of the four poits, then the number of segments of length $a$ would be two, as every segment is counted twice when we count the emanating segments. So we may assume that $A C$ has length $a$, too. If $B C=a$, then $A B C$ would be an equilateral triangle, and the distance of $D$ from each of its vertices would be $b$. This is not possible, since $b>a$. So $B C=b$. Of the segments $C D$ and $B D$ one has length $a$. We may assume $D C=a$. The segments $D C$ and $A B$ are either on one side of thye line $A C$ or on opposite sides of it. In the latter case, $A B C D$ is a parallelogram with a pair of sides of length $a$ and a pair of sides of length $b$, and its diagonals have lengths $a$ and $b$. This is not possible, due to the fact that the sum of the squares of the diagonals of the parallelogram, $a^{2}+b^{2}$, would be equal to the sum of the squares of its sides, i.e. $2 a^{2}+2 b^{2}$. This means that we may assume that $B A C D$ is a convex quadrilateral. Let $\angle A B C=\alpha$ and $\angle A D B=\beta$. From isosceles triangles we obtain for instance $\angle C B D=\beta$, and from the triangle $A B D$ in particular $2 \alpha+2 \beta+\beta=\pi$ as well as $\angle C D A=\alpha, \angle D C B=\frac{1}{2}(\pi-\beta), \angle C A D=\alpha$. The triangle $A D C$ thus yields $\alpha+\alpha+\alpha+\frac{1}{2}(\pi-\beta)=\pi$. From this we solve $\alpha=\frac{1}{5} \pi=36^{\circ}$. The sine theorem applied to $A B C$ gives
$$
\frac{b}{a}=\frac{\sin 108^{\circ}}{\sin 36^{\circ}}=\frac{\sin 72^{\circ}}{\sin 36^{\circ}}=2 \cos 36^{\circ}=\frac{\sqrt{5}+1}{2}
$$
(In fact, $a$ is the side of a regular pentagon, and $b$ is its diagonal.) - Another way of finding the ratio $\frac{b}{a}$ is to consider the trapezium $C D B A$, with $C D \| A B$; if $E$ is the orthogonal projection of $B$ on the segment $C D$, then $C E=b-\frac{1}{2}(b-a)=\frac{1}{2}(b+a)$. The right triangles $B C E$ and $D C E$ yield $C E^{2}=b^{2}-\left(\frac{b+a}{2}\right)^{2}=a^{2}-\left(\frac{b-a}{2}\right)^{2}$, which can be written as $b^{2}-a b-a^{2}=0$. From this we solve $\frac{b}{a}=\frac{\sqrt{5}+1}{2}$.
| \frac{\sqrt{5}+1}{2} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
98.1. Determine all functions $f$ defined in the set of rational numbers and taking their values in the same set such that the equation $f(x+y)+f(x-y)=2 f(x)+2 f(y)$ holds for all rational numbers $x$ and $y$.
|
Solution. Insert $x=y=0$ in the equation to obtain $2 f(0)=4 f(0)$, which implies $f(0)=0$. Setting $x=0$, one obtains $f(y)+f(-y)=2 f(y)$ of $f(-y)=f(y)$. Then assume $y=n x$, where $n$ is a positive integer. We obtain
$$
f((n+1) x)=2 f(x)+2 f(n x)-f((n-1) x)
$$
In particular, $f(2 x)=2 f(x)+2 f(x)-f(0)=4 f(x)$ and $f(3 x)=2 f(x)+2 f(2 x)-f(x)=$ $9 f(x)$. We prove $f(n x)=n^{2} f(x)$ for all positive integers $n$. This is true for $n=1$. Assume $f(k x)=k^{2} f(x)$ for $k \leq n$. Then
$$
\begin{aligned}
& f((n+1) x)=2 f(x)+2 f(n x)-f((n-1) x) \\
& =\left(2+2 n^{2}-(n-1)^{2}\right) f(x)=(n+1)^{2} f(x)
\end{aligned}
$$
and we are done. If $x=1 / q$, where $q$ is a positive integer, $f(1)=f(q x)=q^{2} f(x)$. So $f(1 / q)=f(1) / q^{2}$. This again implies $f(p / q)=p^{2} f(1 / q)=(p / q)^{2} f(1)$. We have shown that there is a rational number $a=f(1)$ such that $f(x)=a x^{2}$ for all positive rational numbers $x$. But since $f$ is an even function, $f(x)=a x^{2}$ for all rational $x$. We still have to check that for every rational $a, f(x)=a x^{2}$ satisfies the conditions of the problem. In fact, if $f(x)=a x^{2}$, then $f(x+y)+f(x-y)=a(x+y)^{2}+a(x-y)^{2}=2 a x^{2}+2 a y^{2}=2 f(x)+2 f(y)$. So the required functions are all functions $f(x)=a x^{2}$ where $a$ is any rational number.
| f(x)=^{2} | Algebra | math-word-problem | Yes | Yes | olympiads | false |
99.1. The function $f$ is defined for non-negative integers and satisfies the condition
$$
f(n)= \begin{cases}f(f(n+11)), & \text { if } n \leq 1999 \\ n-5, & \text { if } n>1999\end{cases}
$$
Find all solutions of the equation $f(n)=1999$.
|
Solution. If $n \geq 2005$, then $f(n)=n-5 \geq 2000$, and the equation $f(n)=1999$ has no solutions. Let $1 \leq k \leq 4$. Then
$$
\begin{gathered}
2000-k=f(2005-k)=f(f(2010-k)) \\
=f(1999-k)=f(f(2004-k))=f(1993-k)
\end{gathered}
$$
Let $k=1$. We obtain three solutions $1999=f(2004)=f(1998)=f(1992)$. Moreover, $1995=f(2000)=f(f(2005))=f(1994)$ and $f(1993)=f(f(2004))=f(1999)=$ $f(f(2010))=f(2005)=2000$. So we have shown that $2000-k=f(1999-k)$, for $k=0,1,2,3,4,5$, and $2000-k=f(1993-k)$ for $k=0,1,2,3,4$. We now show by downwards induction that $f(6 n+1-k)=2000-k$ for $n \leq 333$ and $0 \leq k \leq 5$. This has already been proved for $n=333$ and $n=332$. We assume that the claim is true for $n=m+2$ and $n=m+1$. Then $f(6 m+1-k)=f(f(6 m+12-k))=$ $f(f(6(m+2)+1-(k+1))=f(2000-k-1)=f(1999-k)=2000-k$ for $k=0,1,2,3,4$, and $f(6 m+1-5)=f(6 m-4)=f(f(6 m+7))=f(f(6(m+1)+1))=f(2000)=1995=2000-5$. So the claim is true for $n=m$. Summing up, $1999=2000-1=f(6 n)$, if and only if $n=1,2, \ldots, 334$.
| 1999=f(6n),ifonlyifn=1,2,\ldots,334 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
99.2. Consider 7-gons inscribed in a circle such that all sides of the 7-gon are of different length. Determine the maximal number of $120^{\circ}$ angles in this kind of a 7-gon.
|
Solution. It is easy to give examples of heptagons $A B C D E F G$ inscribed in a circle with all sides unequal and two angles equal to $120^{\circ}$. These angles cannot lie on adjacent vertices of the heptagon. In fact, if $\angle A B C=\angle B C D=120^{\circ}$, and arc $B C$ equals $b^{\circ}$, then arcs $A B$ and $C D$ both are $120^{\circ}-b^{\circ}$ (compute angles in isosceles triangles with center of the circle as the to vertex), and $A B=C D$, contrary to the assumption. So if the heptagon has three angles of $120^{\circ}$, their vertices are, say $A, C$, and $E$. Then each of the arcs $G A B, B C D$, $D E F$ are $360^{\circ}-240^{\circ}=120^{\circ}$. The arcs are disjoint, so they cover the whole circumference. The $F$ has to coincide with $G$, and the heptagon degenerates to a hexagon. There can be at most two $120^{\circ}$ angles.
| 2 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
00.1. In how many ways can the number 2000 be written as a sum of three positive, not necessarily different integers? (Sums like $1+2+3$ and $3+1+2$ etc. are the same.)
|
Solution. Since 3 is not a factor of 2000 , there has to be at least two different numbers among any three summing up to 2000 . Denote by $x$ the number of such sums with three different summands and by $y$ the number of sums with two different summands. Consider 3999 boxes consequtively numbered fron 1 to 3999 such that all boxes labelled by an odd number contain a red ball. Every way to put two blue balls in the even-numbered boxes produces a partition of 2000 in three summands. There are $\binom{1999}{2}=999 \cdot 1999$ ways to place the blue balls. But htere are $3!=6$ different placements, which produce the same partition of 2000 into three different summands, and $\frac{3!}{2}=3$ different placements, which produce the same partition of 2000 into summands two which are equal. Thus $6 x+3 y=$ 1999.999. But $y=999$, because the number appering twice in the partition can be any of the numbers $1,2, \ldots, 999$. This leads to $x=998 \cdot 333$, so $x+y=1001 \cdot 333=333333$.
| 333333 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
00.2. The persons $P_{1}, P_{1}, \ldots, P_{n-1}, P_{n}$ sit around a table, in this order, and each one of them has a number of coins. In the start, $P_{1}$ has one coin more than $P_{2}, P_{2}$ has one coin more than $P_{3}$, etc., up to $P_{n-1}$ who has one coin more than $P_{n}$. Now $P_{1}$ gives one coin to $P_{2}$, who in turn gives two coins to $P_{3}$ etc., up to $P_{n}$ who gives $n$ coins to $P_{1}$. Now the process continues in the same way: $P_{1}$ gives $n+1$ coins to $P_{2}, P_{2}$ gives $n+2$ coins to $P_{3}$; in this way the transactions go on until someone has not enough coins, i.e. a person no more can give away one coin more than he just received. At the moment when the process comes to an end in this manner, it turns out that there are to neighbours at the table such that one of them has exactly five times as many coins as the other. Determine the number of persons and the number of coins circulating around the table.
|
Solution. Assume that $P_{n}$ has $m$ coins in the start. Then $P_{n-1}$ has $m+1$ coins, ... and $P_{1}$ has $m+n-1$ coins. In every move a player receives $k$ coins and gives $k+1$ coins away, so her net loss is one coin. After the first round, when $P_{n}$ has given $n$ coins to $P_{1}$, $P_{n}$ has $m-1$ coins, $P_{n-1}$ has $m$ coins etc., after two rounds $P_{n}$ has $m-2$ coins, $P_{n-1}$ has $m-1$ coins etc. This can go on during $m$ rounds, after which $P_{n}$ has no money, $P_{n-1}$ has one coin etc. On round $m+1$ each player still in possession of money can receive and give away coins as before. The penniless $P_{n}$ can no more give away coins according to the rule. She receives $n(m+1)-1$ coins from $P_{n-1}$, but is unable to give $n(m+1)$ coins to $P_{1}$. So when the game ends, $P_{n-1}$ has no coins and $P_{1}$ has $n-2$ coins. The only pair of neighbours such that one has 5 times as many coins as the other can be $\left(P_{1}, P_{n}\right)$. Because $n-21$, the possibilities are $n=3, m=1$ or $n=9, m=3$. Both are indeed possible. In the first case the number of coins is $3+2+1=6$, in the second $11+10+\cdots+3=63$.
| 6or63 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
01.3. Determine the number of real roots of the equation
$$
x^{8}-x^{7}+2 x^{6}-2 x^{5}+3 x^{4}-3 x^{3}+4 x^{2}-4 x+\frac{5}{2}=0
$$
|
Solution. Write
$$
\begin{gathered}
x^{8}-x^{7}+2 x^{6}-2 x^{5}+3 x^{4}-3 x^{3}+4 x^{2}-4 x+\frac{5}{2} \\
=x(x-1)\left(x^{6}+2 x^{4}+3 x^{2}+4\right)+\frac{5}{2}
\end{gathered}
$$
If $x(x-1) \geq 0$, i.e. $x \leq 0$ or $x \geq 1$, the equation has no roots. If $0x(x-1)=\left(x-\frac{1}{2}\right)^{2}-\frac{1}{4} \geq-\frac{1}{4}$ and $x^{6}+2 x^{4}+3 x+4<1+2+3+4=10$. The value of the left-hand side of the equation now is larger than $-\frac{1}{4} \cdot 10+\frac{5}{2}=0$. The equation has no roots in the interval $(0,1)$ either.
| 0 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
02.2. In two bowls there are in total $N$ balls, numbered from 1 to $N$. One ball is moved from one of the bowls to the other. The average of the numbers in the bowls is increased in both of the bowls by the same amount, $x$. Determine the largest possible value of $x$.
|
Solution. Consider the situation before the ball is moved from urn one to urn two. Let the number of balls in urn one be $n$, and let the sum of numbers in the balls in that urn be $a$. The number of balls in urn two is $m$ and the sum of numbers $b$. If $q$ is the number written in the ball which was moved, the conditions of the problem imply
$$
\left\{\begin{array}{l}
\frac{a-q}{n-1}=\frac{a}{n}+x \\
\frac{b+q}{m+1}=\frac{b}{m}+x
\end{array}\right.
$$
or
$$
\left\{\begin{array}{l}
a=n q+n(n-1) x \\
b=m q-m(m+1) x
\end{array}\right.
$$
Because $n+m=N$ and $a+b=\frac{1}{2} N(N+1)$, we obtain
$$
\frac{1}{2} N(N+1)=N q+x\left(n^{2}-m^{2}-N\right)=N q+x N(n-m-1)
$$
and $q=\frac{1}{2}(N+1)-x(n-m-1), b=\frac{1}{2} m(N+1)-x m n$. But $b \geq 1+2+\cdots+m=\frac{1}{2} m(m+1)$. So $\frac{1}{2}(N+1)-x n=\frac{1}{2}(m+n+1)-x n \geq \frac{1}{2}(m+1)$ or $\frac{n}{2}-x n \geq 0$. Hence $x \leq \frac{1}{2}$. The inequality is sharp or $x=\frac{1}{2}$, when the nubers in the balls in urn one are $m+1, m+2$, $\ldots, N$, the numbers in urn two are $1,2, \ldots, m$, and $q=m+1$.
| \frac{1}{2} | Algebra | math-word-problem | Yes | Yes | olympiads | false |
02.4. Eva, Per and Anna play with their pocket calculators. They choose different integers and check, whether or not they are divisible by 11. They only look at nine-digit numbers consisting of all the digits 1, 2, .., 9. Anna claims that the probability of such a number to be a multiple of 11 is exactly 1/11. Eva has a different opinion: she thinks the probability is less than $1 / 11$. Per thinks the probability is more than $1 / 11$. Who is correct?
|
Solution. We write the numbers in consideration, $n=a_{0}+10 a_{1}+10^{2} a_{2}+\cdots+10^{8} a_{8}$, in the form
$$
\begin{gathered}
a_{0}+(11-1) a_{1}+(99+1) a_{2}+(1001-1) a_{3} \\
+(9999+1) a_{4}+(100001-1) a_{5}+(999999+1) a_{6} \\
\quad+(10000001-1) a_{7}+(99999999+1) a_{8} \\
=\left(a_{0}-a_{1}+a_{2}-a_{3}+a_{4}-a_{5}+a_{6}-a_{7}+a_{8}\right)+11 k \\
=\left(a_{0}+a_{1}+\cdots+a_{8}\right)-2\left(a_{1}+a_{3}+a_{5}+a_{7}\right)+11 k \\
=44+1+11 k-2\left(a_{1}+a_{3}+a_{5}+a_{7}\right)
\end{gathered}
$$
So $n$ is divisible by 11 if and only if $2\left(a_{1}+a_{3}+a_{5}+a_{7}\right)-1$ is divisible by 11 . Let $s=a_{1}+a_{3}+a_{5}+a_{7}$. Then $1+2+3+4=10 \leq s \leq 6+7+8+9=30$ and $19 \leq 2 s-1 \leq 59$. The only multiples of 11 in the desired interval are 33 and 55 , so $s=17$
or $s=28$. If $s=17$, the smallest number in the set $A=\left\{a_{1}, a_{3}, a_{5}, a_{7}\right\}$ is either 1 or 2 $(3+4+5+6=18)$. Checking the cases, we see that there are 9 possible sets $A:\{2,4,5,6\}$, $\{2,3,5,7\},\{2,3,4,8\},\{1,4,5,7\},\{1,3,6,7\},\{1,3,5,8\},\{1,3,4,9\},\{1,2,6,8\}$, and $\{1,2,5,9\}$. If $s=28$, the largest number in $A$ is $9(5+6+7+8=26)$ and the second largest $8(5+6+7+9=27)$. The only possible $A$ 's are $\{4,7,8,9\}$ and $\{5,6,8,9\}$. The number of different ways to choose the set $A$ is $\binom{9}{4}=\frac{9 \cdot 8 \cdot 7 \cdot 6}{2 \cdot 3 \cdot 4}=126$. Of these, the number of choices leading to a number which is a multiple of 11 is $9+2=11$. This means that the probability of picking a number which is divisible by 11 is $\frac{11}{126}<\frac{11}{121}=\frac{1}{11}$. So Eva's opinion is correct.
| \frac{11}{126}<\frac{1}{11} | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
03.2. Find all triples of integers $(x, y, z)$ satisfying
$$
x^{3}+y^{3}+z^{3}-3 x y z=2003
$$
|
Solution. It is a well-known fact (which can be rediscovered e.g. by noticing that the left hand side is a polynomial in $x$ having $-(y+z)$ as a zero) that
$$
\begin{aligned}
& x^{3}+y^{3}+z^{3}-3 x y z=(x+y+z)\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right) \\
&=(x+y+z) \frac{(x-y)^{2}+(y-z)^{2}+(z-x)^{2}}{2}
\end{aligned}
$$
The second factor in the right hand side is non-negative. It is not hard to see that 2003 is a prime. So the solutions of the equation either satisfy
$$
\left\{\begin{aligned}
x+y+z & =1 \\
(x-y)^{2}+(y-z)^{2}+(z-x)^{2} & =4006
\end{aligned}\right.
$$
or
$$
\left\{\begin{aligned}
x+y+z & =2003 \\
(x-y)^{2}+(y-z)^{2}+(z-x)^{2} & =2
\end{aligned}\right.
$$
Square numbers are $\equiv 0$ or $\equiv 1 \bmod 3$. So in the first case, exactly two of the squares $(x-y)^{2},(y-z)^{2}$, and $(z-x)^{2}$ are multiples of 3. Clearly this is not possible. So we must have $x+y+z=2003$ and $(x-y)^{2}+(y-z)^{2}+(z-x)^{2}=2$. This is possible if and only if one of the squares is 0 and two are 1's. So two of $x, y, z$ have to be equal and the third must differ by 1 of these. This means that two of the numbers have to be 668 and one 667. A substitution to the original equation shows that this necessary condition is also sufficient.
| (668,668,667) | Algebra | math-word-problem | Yes | Yes | olympiads | false |
03.4. Let $\mathbb{R}^{*}=\mathbb{R} \backslash\{0\}$ be the set of non-zero real numbers. Find all functions $f: \mathbb{R}^{*} \rightarrow \mathbb{R}^{*}$ satisfying
$$
f(x)+f(y)=f(x y f(x+y))
$$
for $x, y \in \mathbb{R}^{*}$ and $x+y \neq 0$.
|
Solution. If $x \neq y$, then
$$
f(y)+f(x-y)=f(y(x-y) f(x))
$$
Because $f(y) \neq 0$, we cannot have $f(x-y)=f(y(x-y) f(x))$ or $x-y=y(x-y) f(x)$. So for all $x \neq y, y f(x) \neq 1$. The only remaining possibility is $f(x)=\frac{1}{x}$. - One easily checks that $f, f(x)=\frac{1}{x}$, indeed satisfies the original functional equation.
| f(x)=\frac{1}{x} | Algebra | math-word-problem | Yes | Yes | olympiads | false |
04.1. 27 balls, labelled by numbers from 1 to 27, are in a red, blue or yellow bowl. Find the possible numbers of balls in the red bowl, if the averages of the labels in the red, blue, and yellow bowl are 15, 3 ja 18, respectively.
|
Solution. Let $R, B$, and $Y$, respectively, be the numbers of balls in the red, blue, and yellow bowl. The mean value condition implies $B \leq 5$ (there are at most two balls with a number $3$ ). $R, B$ and $Y$ satisfy the equations
$$
\begin{aligned}
R+B+Y & =27 \\
15 R+3 S+18 Y & =\sum_{j=1}^{27} j=14 \cdot 27=378
\end{aligned}
$$
We eliminate $S$ to obtain $4 R+5 Y=99$. By checking the possibilities we note that the pairs of positive integers satisfying the last equation are $(R, Y)=(21,3),(16,7),(11,11)$, $(6,15)$, and $(1,19)$. The last two, however, do not satisfy $B=27-(R+Y) \leq 5$. We still have to ascertain that the three first alternatives are possible. In the case $R=21$ we can choose the balls $5,6, \ldots, 25$, in the red bowl, and 2,3 and 4 in the blue bowl; if $P=16$, $7,8, \ldots, 14,16,17, \ldots, 23$, can go to the red bowl and $1,2,4$ and 5 in the blue one, and if $P=11$, the red bowl can have balls $10,11, \ldots 20$, and the blue one $1,2,3,4,5$. The red bowl can contain 21,16 or 11 balls.
| 21,16,11 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
05.1. Find all positive integers $k$ such that the product of the digits of $k$, in the decimal system, equals
$$
\frac{25}{8} k-211
$$
|
Solution. Let
$$
a=\sum_{k=0}^{n} a_{k} 10^{k}, \quad 0 \leq a_{k} \leq 9, \text { for } 0 \leq k \leq n-1,1 \leq a_{n} \leq 9
$$
Set
$$
f(a)=\prod_{k=0}^{n} a_{k}
$$
Since
$$
f(a)=\frac{25}{8} a-211 \geq 0
$$
$a \geq \frac{8}{25} \cdot 211=\frac{1688}{25}>66$. Also, $f(a)$ is an integer, and $\operatorname{gcf}(8,25)=1$, so $8 \mid a$. On the other hand,
$$
f(a) \leq 9^{n-1} a_{n} \leq 10^{n} a_{n} \leq a
$$
So
$$
\frac{25}{8} a-211 \leq a
$$
or $a \leq \frac{8}{17} \cdot 211=\frac{1688}{17}<100$. The only multiples of 8 between 66 and 100 are $72,80,88$, and 96. Now $25 \cdot 9-211=17=7 \cdot 2,25 \cdot 10-211=39 \neq 8 \cdot 0,25 \cdot 11-211=64=8 \cdot 8$, and $25 \cdot 12-211=89 \neq 9 \cdot 6$. So 72 and 88 are the numbers asked for.
| 7288 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
06.2. The real numbers $x, y$ and $z$ are not all equal and satisfy
$$
x+\frac{1}{y}=y+\frac{1}{z}=z+\frac{1}{x}=k
$$
Determine all possible values of $k$.
|
Solution. Let $(x, y, z)$ be a solution of the system of equations Since
$$
x=k-\frac{1}{y}=\frac{k y-1}{y} \quad \text { and } \quad z=\frac{1}{k-y}
$$
the equation
$$
\frac{1}{k-y}+\frac{y}{k y-1}=k
$$
to be simplified into
$$
\left(1-k^{2}\right)\left(y^{2}-k y+1\right)=0
$$
is true. So either $|k|=1$ or
$$
k=y+\frac{1}{y}
$$
The latter alternative, substituted to the original equations, yields immediately $x=y$ and $z=y$. So $k= \pm 1$ is the only possibility. If $k=1$, for instance $x=2, y=-1$ and $z=\frac{1}{2}$ is a solution; if $k=-1$, a solution is obtained by reversing the signs for a solution with $k=1$. So $k=1$ and $k=-1$ are the only possible values for $k$.
| \1 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
06.3. A sequence of positive integers $\left\{a_{n}\right\}$ is given by
$$
a_{0}=m \quad \text { and } \quad a_{n+1}=a_{n}^{5}+487
$$
for all $n \geq 0$. Determine all values of $m$ for which the sequence contains as many square numbers as possible.
|
Solution. Consider the expression $x^{5}+487$ modulo 4. Clearly $x \equiv 0 \Rightarrow x^{5}+487 \equiv 3$, $x \equiv 1 \Rightarrow x^{5}+487 \equiv 0 ; x \equiv 2 \Rightarrow x^{5}+487 \equiv 3$, and $x \equiv 3 \Rightarrow x^{5}+487 \equiv 2$. Square numbers are always $\equiv 0$ or $\equiv 1 \bmod 4$. If there is an even square in the sequence, then all subsequent numbers of the sequence are either $\equiv 2$ or $\equiv 3 \bmod 4$, and hence not squares. If there is an odd square in the sequence, then the following number in the sequence can be an even square, but then none of the other numbers are squares. So the maximal number of squares in the sequence is two. In this case the first number of the sequence has to be the first square, since no number of the sequence following another one satisfies $x \equiv 1 \bmod 4$. We have to find numbers $k^{2}$ such that $k^{10}+487=n^{2}$. We factorize $n^{2}-k^{10}$. Because 487 is a prime, $n-k^{5}=1$ and $n+k^{5}=487$ or $n=244$ and $k=3$. The only solution of the problem thus is $m=3^{2}=9$.
| 9 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
07.1. Find one solution in positive integers to the equation
$$
x^{2}-2 x-2007 y^{2}=0
$$
|
Solution. The equation can be written in the form
$$
x(x 2)=223 \cdot(3 y)^{2}
$$
Here the prime number 223 must divide $x$ or $x 2$. In fact, for $x=225$ we get $x(x 2)=$ $15^{2} \cdot 223$, which is equivalent to $223 \cdot(3 y)^{2}$ for $y=5$. Thus, $(x, y)=(225,5)$ is one solution.
| (225,5) | Algebra | math-word-problem | Yes | Yes | olympiads | false |
08.1. Determine all real numbers $A, B$ and $C$ such that there exists a real function $f$ that satisfies
$$
f(x+f(y))=A x+B y+C
$$
for all real $x$ and $y$.
|
Solution. Let $A, B$ and $C$ be real numbers and $f$ a function such that $f(x+f(y))=$ $A x+B y+C$ for all $x$ and $y$. Let $z$ be a real number and set $x=z-f(0)$ and $y=0$. Then
$$
f(z)=f(z-f(0)+f(0))=A(z-f(0))+B \cdot 0+C=A z-A f(0)+C
$$
so there are numbers $a$ and $b$ such that $f(z)=a z+b$ for all $z$. Now $f(x+f(g))=$ $a x+a^{2} y+(a+1) b$, and $(A, B, C)=\left(a, a^{2},(a+1) b\right)$, where $a$ and $b$ are arbitrary real numbers, that is, $(A, B, C)=\left(a, a^{2}, c\right)$, where $a \neq-1$ and $c$ are arbitrary, or $(A, B, C)=(-1,1,0)$
| (A,B,C)=(,^2,)where\neq-1arbitrary,or(A,B,C)=(-1,1,0) | Algebra | math-word-problem | Yes | Yes | olympiads | false |
08.2. Assume that $n \geq 3$ people with different names sit around a round table. We call any unordered pair of them, say $M$ and $N$, dominating, if
(i) $M$ and $N$ do not sit on adjacent seats, and
(ii) on one (or both) of the arcs connecting $M$ and $N$ along the table edge, all people have names that come alphabetically after the names of $M$ and $N$.
Determine the minimal number of dominating pairs.
|
Solution. We will show by induction that the number of dominating pairs (hence also the minimal number of dominating pairs) is $n-3$ for $n \geq 3$. If $n=3$, all pairs of people sit on adjacent seats, so there are no dominating pairs. Assume that the number of dominating pairs is $n-3$ for some $n>3$. If there are $n+1$ people around the table, let the person whose name is alphabetically last leave the table. The two people sitting next to that person, who formed a dominating pair, no longer do. On the other hand, any other dominating pair remains a dominating pair in the new configuration of $n$ people, and any dominating pair in the new configuration was also a dominating pair in the old. The number of dominating pairs in the new configuration is $n-3$, so the number in the old was $(n+1)-3$.
| n-3 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
09.2. On a faded piece of paper it is possible, with some effort, to discern the following:
$$
\left(x^{2}+x+a\right)\left(x^{15}-\ldots\right)=x^{17}+x^{13}+x^{5}-90 x^{4}+x-90
$$
Some parts have got lost, partly the constant term of the first factor of the left side, partly the main part of the other factor. It would be possible to restore the polynomial forming the other factor, but we restrict ourselves to asking the question: What is the value of the constant term a? We assume that all polynomials in the statement above have only integer coefficients.
|
Solution. We denote the polynomial $x^{2}+x+a$ by $P_{a}(x)$, the polynomial forming the other factor of the left side by $Q(x)$ and the polynomial on the right side by $R(x)$. The polynomials are integer valued for every integer $x$. For $x=0$ we get $P_{a}(0)=a$ and $R(0)=-90$, so $a$ is a divisor of $90=2 \cdot 3 \cdot 3 \cdot 5$. For $x=-1$ we get $P_{a}(-1)=-184$, so $a$ is also a divisor of $184=2 \cdot 2 \cdot 2 \cdot 23$. But the only prime factor in common is 2 . So the only possibilities for $a$ are $\pm 2$ and $\pm 1$. If $a=1$, we get for $x=1$ that $P_{1}(1)=3$, while $R(1)=4-180=-176$, which cannot be divided by 3 . If $a=-2$ we get for $x=1$ that $P_{2}(1)=0$, i.e. the left side is equal to 0 , while the right side is equal to $R(1)=-176$, which is different from 0 . Neither $a=1$ nor $a=-2$ will thus work. It remains to check $a=2$ and $a=-1$. Before we use the procedure above again, we need a factorization of $R(x)$. We observe that $x^{4}+1$ is a divisor of $R(x)$, since the right side may be written as $\left(x^{4}+1\right)\left(x^{13}+x-90\right)$. If $a=-1$ we get for $x=2$ that $P_{1}(2)=5$, while $x^{4}+1=17$ and $x^{13}+x-90=8104$. So the right hand side is not divisible by 5 . Now, the only remaining possibility is $a=2$, i.e. $x^{2}+x+2$ is a divisor of $R(x)$.
| 2 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
10.3. Laura has 2010 lamps connected with 2010 buttons in front of her. For each button, she wants to know the corresponding lamp. In order to do this, she observes which lamps are lit when Richard presses a selection of buttons. (Not pressing anything is also a possible selection.) Richard always presses the buttons simultaneously, so the lamps are lit simultaneously, too.
a) If Richard chooses the buttons to be pressed, what is the maximum number of different combinations of buttons he can press until Laura can assign the buttons to the lamps correctly?
b) Supposing that Laura will choose the combinations of buttons to be pressed, what is the minimum number of attempts she has to do until she is able to associate the buttons with the lamps in a correct way?
|
Solution. a) Let us say that two lamps are separated, if one of the lamps is turned on while the other lamp remains off. Laura can find out which lamps belong to the buttons if every two lamps are separated. Let Richard choose two arbitrary lamps. To begin with, he turns both lamps on and then varies all the other lamps in all possible ways. There are $2^{2008}$ different combinations for the remaining $2010-2=2008$ lamps. Then Richard turns
the two chosen lamps off. Also, at this time there are $2^{2008}$ combinations for the remaining lamps. Consequently, for the $2^{2009}$ combinations in all, it is not possible to separate the two lamps of the first pair. However, we cannot avoid the separation if we add one more combination. Indeed, for every pair of lamps, we see that if we turn on a combination of lamps $2^{2009}+1$ times, there must be at least one setup where exactly one of the lamps is turned on and the other is turned off. Thus, the answer is $2^{2009}+1$.
b) For every new step with a combination of lamps turned on, we get a partition of the set of lamps into smaller and smaller subsets where elements belonging to the same subset cannot be separated. In each step every subset is either unchanged or divided into two smaller parts, i.e. the total number of subsets after $\mathrm{k}$ steps will be at most $2^{k}$. We are finished when the number of subsets is equal to 2010 , so the answer is at least $\left\lceil\log _{2} 2010\right\rceil=11$. But it is easy to see that Laura certainly can choose buttons in every step in such a way that there are at most $2^{11-k}$ lamps in every part of the partition after $k$ steps. Thus, the answer is 11 .
| 11 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
10.4. A positive integer is called simple if its ordinary decimal representation consists entirely of zeroes and ones. Find the least positive integer $k$ such that each positive integer $n$ can be written as $n=a_{1} \pm a_{2} \pm a_{3} \pm \cdots \pm a_{k}$, where $a_{1}, \ldots, a_{k}$ are simple.
|
Solution. We can always write $n=a_{l}+a_{2}+\cdots+a_{9}$ where $a_{j}$ has 1 's in the places where $n$ has digits greater or equal to $j$ and 0 's in the other places. So $k \leq 9$. To show that $k \geq 9$, consider $n=10203040506070809$. Suppose $n=a_{l}+a_{2}+\cdots+a_{j}-a_{j+l}-a_{j+2}-\cdots-a_{k}$, where $a_{l}, \ldots, a_{k}$ are simple, and $k<9$. Then all digits of $b_{l}=a_{l}+\cdots+a_{j}$ are not greater than $j$ and all digits of $b_{2}=a_{j+l}+\cdots+a_{k}$ are not greater than $k-j$. We have $n+b_{2}=b_{l}$. We perform column addition of $n$ and $b_{2}$ and consider digit $j+1$ in the number $n$. There will be no carry digit coming from lower decimal places, since the sum there is less that $10 \ldots 0+88 \ldots 8=98 \ldots 8$. So in the column of $j+1$ we get the sum of $j+1$ and the corresponding digit in $b_{2}$. The resulting digit should be less than $j+1$. Thus in the corresponding place in $b_{2}$ we have at least $9-j$. But $9-j \leq k-j$, implying $k \geq 9$. Hence, we have proved that the maximal $k$ is 9 .
| 9 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
## Problem 2
Let $A B C D$ be a cyclic quadrilateral satisfying $A B=A D$ and $A B+B C=C D$.
Determine $\angle C D A$.
|
Solution 2 Answer: $\angle C D A=60^{\circ}$.
Choose the point $E$ on the segment $C D$ such that $D E=A D$. Then $C E=C D-A D=$ $C D-A B=B C$, and hence the triangle $C E B$ is isosceles.
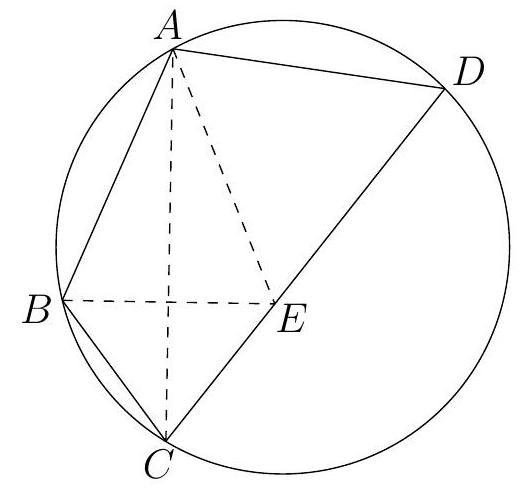
Now, since $A B=A D$ then $\angle B C A=\angle A C D$. This shows that $C A$ is the bisector of $\angle B C D=\angle B C E$. In an isosceles triangle, the bisector of the apex angle is also the perpendicular bisector of the base. Hence $A$ is on the perpendicular bisector of $B E$, and $A E=A B=A D=D E$. This shows that triangle $A E D$ is equilateral, and thus $\angle C D A=60^{\circ}$.
| 60 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
## Problem 3
Find all $a \in \mathbb{R}$ for which there exists a function $f: \mathbb{R} \rightarrow \mathbb{R}$, such that
(i) $f(f(x))=f(x)+x$, for all $x \in \mathbb{R}$,
(ii) $f(f(x)-x)=f(x)+$ ax, for all $x \in \mathbb{R}$.
|
Solution 3 Answer: $a=\frac{1 \pm \sqrt{5}}{2}$.
From (i) we get $f(f(f(x))-f(x))=f(x)$. On the other hand (ii) gives
$$
f(f(f(x))-f(x))=f(f(x))+a f(x)
$$
Thus we have $(1-a) f(x)=f(f(x))$. Now it follows by (i) that $(1-a) f(x)=f(x)+x$, and hence $f(x)=-\frac{1}{a} x$, since $a=0$ obviously does not give a solution.
We now need to check whether (i) and (ii) hold for this function for some values of $a$ and all real $x$. We have
$$
f(f(x))=-\frac{1}{a} f(x)=\frac{1}{a^{2}} x, \text { and } f(x)+x=-\frac{1}{a} x+x=\frac{a-1}{a} x
$$
Thus (i) will hold for all real $x$ iff $\frac{1}{a^{2}}=\frac{a-1}{a}$, i.e. iff $a=\frac{1 \pm \sqrt{5}}{2}$. For these values of $a$ we have
$$
f(f(x)-x)=-\frac{1}{a}(f(x)-x)=-\frac{1}{a}\left(-\frac{1}{a} x-x\right)=\left(\frac{1}{a^{2}}+\frac{1}{a}\right) x=\frac{a+1}{a^{2}} x=x
$$
and
$$
f(x)+a x=-\frac{1}{a} x+a x=\frac{a^{2}-1}{a} x=x
$$
so that for these two values of $a$ both (i) and (ii) hold for all real $x$. Thus the values of $a$ such that there exists a function $f$ with the desired properties are $a=\frac{1 \pm \sqrt{5}}{2}$.
| \frac{1\\sqrt{5}}{2} | Algebra | math-word-problem | Yes | Yes | olympiads | false |
## Problem 4
King George has decided to connect the 1680 islands in his kingdom by bridges. Unfortunately the rebel movement will destroy two bridges after all the bridges have been built, but not two bridges from the same island.
What is the minimal number of bridges the King has to build in order to make sure that it is still possible to travel by bridges between any two of the 1680 islands after the rebel movement has destroyed two bridges?
|
Solution 4 Answer: 2016
An island cannot be connected with just one bridge, since this bridge could be destroyed. Consider the case of two islands, each with only two bridges, connected by a bridge. (It is not possible that they are connected with two bridges, since then they would be isolated from the other islands no matter what.) If they are also connected to two separate islands, then they would be isolated if the rebel movement destroys the two bridges from these islands not connecting the two. So the two bridges not connecting them must go to the same island. That third island must have at least two other bridges, otherwise the rebel movement could cut off these three islands.
Suppose there is a pair of islands with exactly two bridges that are connected to each other. From the above it is easy to see that removing the pair (and the three bridges connected to them) must leave a set of islands with the same properties. Continue removing such pairs, until there are none left. (Note that the reduced set of islands could have a new such pair and that also needs to be removed.) Suppose we are left with $n$ islands and since two islands are removed at a time, $n$ must be an even number. And from the argument above it is clear that $n \geq 4$.
Consider the remaining set of islands and let $x$ be the number of islands with exactly two bridges (which now are not connected to each other). Then $n-x$ islands have at least three bridges each. Let $B^{\prime}$ be the number of bridges in the reduced set. Now $B^{\prime} \geq 2 x$ and $2 B^{\prime} \geq 2 x+3(n-x)=3 n-x$. Hence $2 B^{\prime} \geq \max (4 x, 3 n-x) \geq 4 \cdot \frac{3 n}{5}$, and thus $B^{\prime} \geq \frac{6 n}{5}$. Now let $B$ be the number of bridges in the original set. Then
$$
B=B^{\prime}+3 \cdot \frac{1680-n}{2} \geq \frac{6 n}{5}+\frac{6(1680-n)}{4} \geq \frac{6 \cdot 1680}{5}=2016
$$
It is possible to construct an example with exactly 2016 bridges: Take 672 of the islands and number them $0,1,2, \ldots 671$. Connect island number $i$ with the islands numbered $i-1$, $i+1$ and $i+336$ (modulo 672). This gives 1008 bridges. We now have a circular path of 672 bridges: $0-1-2-\cdots-671-0$. If one of these 672 bridges are destroyed, the 672 islands are still connected. If two of these bridges are destroyed, the path is broken into two parts. Let $i$ be an island on the shortest path (if they have the same length, just pick a random one). Then island $i+336$ (modulo 672) must be on the other part of the path, and the bridge connecting these two islands will connect the two paths. Hence no matter which two bridges the rebel movement destroys, it is possible to travel between any of the 672 islands.
Now for every of the 1008 bridges above, replace it with two bridges with a new island between the two. This increases the number of bridges to 2016 and the number of islands to $672+1008=1680$ completing the construction. Since the rebel movement does not destroy two bridges from the same island, the same argument as above shows that with this construction it is possible to travel between any of the 1680 islands after the destruction of the two bridges.
| 2016 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
## Problem 1
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f(f(x) f(1-x))=f(x) \quad \text { and } \quad f(f(x))=1-f(x)
$$
for all real $x$.
|
Solution 1. Notice that $f(f(f(x)))=^{2} 1-f(f(x))={ }^{2} f(x)$. This is equation 3 . By substituting $f(x)$ for $x$ in the first equation we get:
$$
f(\underline{f(x)})={ }^{1} f(f(\underline{f(x)}) f(1-\underline{f(x)}))={ }^{2} f(f(f(x)) f(f(f(x))))={ }^{3} f(f(f(x)) f(x))
$$
Again we substitute $f(x)$ for $x$ above:
$$
f(f(\underline{f(x)}))=f(f(f(\underline{f(x)})) f(\underline{f(x)}))
$$
Equation 3 applied on both sides gives us:
$$
f(x)=f(f(x) f(f(x)))
$$
But this is the same as what we started with so
$$
f(x)=f(f(x) f(f(x)))=f(f(x))={ }^{2} 1-f(x)
$$
Therefore $f(x)=\frac{1}{2}$, which is a solution.
| f(x)=\frac{1}{2} | Algebra | math-word-problem | Yes | Yes | olympiads | false |
Problem 3. Find the smallest positive integer $n$, such that there exist $n$ integers $x_{1}, x_{2}, \ldots, x_{n}$ (not necessarily different), with $1 \leq x_{k} \leq n, 1 \leq k \leq n$, and such that
$$
x_{1}+x_{2}+\cdots+x_{n}=\frac{n(n+1)}{2}, \quad \text { and } \quad x_{1} x_{2} \cdots x_{n}=n!
$$
but $\left\{x_{1}, x_{2}, \ldots, x_{n}\right\} \neq\{1,2, \ldots, n\}$.
|
Solution. If it is possible to find a set of numbers as required for some $n=k$, then it will also be possible for $n=k+1$ (choose $x_{1}, \ldots, x_{k}$ as for $n=k$, and
let $x_{k+1}=k+1$ ). Thus we have to find a positive integer $n$ such that a set as required exists, and prove that such a set does not exist for $n-1$.
For $n=9$ we have $8+6+3=9+4+4$, and $8 \cdot 6 \cdot 3=9 \cdot 4 \cdot 4$, so that a set of numbers as required will exist for all $n \geq 9$. It remains to eliminate $n=8$.
Assume $x_{1}, \ldots, x_{8}$ are numbers that satisfy the conditions of the problem. Since 5 and 7 are primes, and since $2 \cdot 5>8$ and $2 \cdot 7>8$, two of the $x$-numbers have to be equal to 5 and 7 ; without loss of generality we can assume that $x_{1}=5, x_{2}=7$. For the remaining numbers we have $x_{3} x_{4} \cdots x_{8}=2^{7} \cdot 3^{2}$, and $x_{3}+x_{4}+\cdots+x_{8}=36-12=24$. Since $3^{2}=9>8$, it follows that exactly two of the numbers $x_{3}, \ldots, x_{8}$ are divisible by 3 , and the rest of the numbers are powers of 2. There are three possible cases to consider: two of the numbers are equal to 3 ; two of the numbers are equal to 6 ; one number is equal to 3 and another one is equal to 6 .
Case 1. $x_{3}=x_{4}=3$
We then have $x_{5}+x_{6}+x_{7}+x_{8}=18$, and $x_{5} x_{6} x_{7} x_{8}=2^{7}$. The possible powers of 2 with sum 18 are $(1,1,8,8)$ and $(2,4,4,8)$, none of them gives the product $2^{7}$.
Case 2. $x_{3}=3, x_{4}=6$
We have $x_{5}+x_{6}+x_{7}+x_{8}=15$, and $x_{5} x_{6} x_{7} x_{8}=2^{6}$. It is immediate to check that the only possibility for the remaining numbers is $(1,2,4,8)$, which is not allowed, since it gives $\left\{x_{1}, x_{2}, \ldots, x_{8}\right\}=\{1,2, \ldots, 8\}$.
Case 3. $x_{3}=x_{4}=6$
Now we have $x_{5}+x_{6}+x_{7}+x_{8}=12$, and $x_{5} x_{6} x_{7} x_{8}=2^{5}$. The possible powers of 2 which give the correct sum are $(1,1,2,8)$ and $(2,2,4,4)$, but again, they do not give the desired product.
Thus the smallest positive integer with the required property is 9 .
| 9 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
Problem 4. The number 1 is written on the blackboard. After that a sequence of numbers is created as follows: at each step each number $a$ on the blackboard is replaced by the numbers $a-1$ and $a+1$; if the number 0 occurs, it is erased immediately; if a number occurs more than once, all its occurrences are left on the blackboard. Thus the blackboard will show 1 after 0 steps; 2 after 1 step; 1,3 after 2 steps; 2, 2, 4 after 3 steps, and so on. How many numbers will there be on the blackboard after $n$ steps?
|
Solution I. Let $S$ be a set of different numbers, all of them less than $2^{n-1}$, and create two new sets as follows: $S_{1}$, consisting of all the numbers in $S$ except
the smallest one, and $S_{2}$, with elements the smallest element of $S$ and all the numbers we get by adding $2^{n-1}$ to each number in $S$. Note that if the number of elements in $S$ is $a$, then $S_{1}$ has $a-1$ elements, and $S_{2}$ has $a+1$ elements. This corresponds to the operations we are allowed to perform on the blackboard, if we throw away all empty sets. If we now operate simultaneously on the sets and on the numbers, then after $n$ steps the number of sets will be exactly equal to the number of numbers on the blackboard.
Let us see what the set operations look like. We must start with a set, consisting only of the number 0 . Next we get an empty set (thrown away), and the set $\{0,1\}$; next the sets $\{1\}$ and $\{0,2,3\}$; next again (an empty set and) $\{1,5\},\{2,3\},\{0,4,6,7\}$, etc.
It is now fairly easy to prove by induction that after $n$ steps
(1) each number less than $2^{n}$ appears in exactly one set;
(2) the number of elements in the sets corresponds exactly to the numbers on the blackboard;
(3) if the numbers in each set are written in increasing order, then the difference between two neighbours is a power of 2 ; thus the binary representations of two neighbours differ in exactly one position (in the binary system the example above looks like this: $\{0\} ;\{0,1\} ;\{01\},\{00,10,11\} ;\{001,101\},\{010,011\}$, $\{000,100,110,111\}) ;$
(4) if $k$ is the number of ones in the binary code of the smallest number of a set, and $l$ the number of ones in the largest number of the same set, then $k+l=n$; (5) each set contains exactly one number with $\left\lfloor\frac{n}{2}\right\rfloor$ ones.
The last property tells us that the number of sets after $n$ steps is equal to the number of numbers such that their binary representation contains exactly $\left\lfloor\frac{n}{2}\right\rfloor$ ones out of $n$ digits, i.e. the number of numbers on the blackboard after $n$ steps will be equal to $\binom{n}{\left\lfloor\frac{n}{2}\right\rfloor}$.
| \binom{n}{\lfloor\frac{n}{2}\rfloor} | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
## Problem 2.
Find the primes $p, q, r$, given that one of the numbers $p q r$ and $p+q+r$ is 101 times the other.
|
Solution. We may assume $r=\max \{p, q, r\}$. Then $p+q+r \leq 3 r$ and $p q r \geq 4 r$. So the sum of the three primes is always less than their product. The only relevant requirement thus is $p q r=101(p+q+r)$. We observe that 101 is a prime. So one of $p, q, r$ must be 101. Assume $r=101$. Then $p q=p+q+101$. This can be written as $(p-1)(q-1)=102$. Since $102=1 \cdot 102=2 \cdot 51=3 \cdot 34=6 \cdot 17$, the possibilities for $\{p, q\}$ are $\{2,103\},\{3,52\},\{4,35\},\{7,18\}$ The only case, where both the numbers are primes, is $\{2,103\}$. So the only solution to the problem is $\{p, q, r\}=\{2,101,103\}$.
| {2,101,103} | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
## Problem 4.
An encyclopedia consists of 2000 numbered volumes. The volumes are stacked in order with number 1 on top and 2000 in the bottom. One may perform two operations with the stack:
(i) For $n$ even, one may take the top $n$ volumes and put them in the bottom of the stack without changing the order.
(ii) For $n$ odd, one may take the top $n$ volumes, turn the order around and put them on top of the stack again.
How many different permutations of the volumes can be obtained by using these two operations repeatedly?
|
Solution 1. (By the proposer.) Let the positions of the books in the stack be $1,2,3, \ldots, 2000$ from the top (and consider them modulo 2000). Notice that both operations fix the parity of the number of the book at a any given position. Operation (i) subtracts an even integer from the number of the book at each position. If $A$ is an operation of type (i), and $B$ is an operation of type (ii), then the operation $A^{-1} B A$ changes the order of the books in the positions $n+1$ to $n+m$ where $n$ is even and $m$ is odd. This is called turning the interval.
Now we prove that all the volumes in odd positions can be placed in the odd positions in every way we like: If the volume we want in position 1 is in position $m_{1}$, we turn the interval 1 to $m_{1}$. Now if the volume we want in position 3 is in position $m_{3}$, we turn the interval 3 to $m_{3}$, and so on. In this way we can permute the volumes in odd positions exactly as we want to.
Now we prove that we can permute the volumes in even positions exactly as we want without changing the positions of the volumes in the odd positions: We can make a transposition of the two volumes in position $2 n$ and $2 n+2 m$ by turning the interval $2 n+1$ to $2 n+2 m-1$, then turning the interval $2 n+2 m+1$ to $2 n-1$, then turning the interval $2 n+1$ to $2 n-1$, and finally adding $2 m$ to the number of the volume in each position.
Since there are 1000! permutations of the volumes in the odd positions, and 1000! permutations of the volumes in the even positions, altogether we have (1000!) ${ }^{2}$ different permutations.
| (1000!)^2 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Problem 2. In a football tournament there are $n$ teams, with $n \geq 4$, and each pair of teams meets exactly once. Suppose that, at the end of the tournament, the final scores form an arithmetic sequence where each team scores 1 more point than the following team on the scoreboard. Determine the maximum possible score of the lowest scoring team, assuming usual scoring for football games (where the winner of a game gets 3 points, the loser 0 points, and if there is a tie both teams get 1 point).
|
Solution. Note that the total number of games equals the number of different pairings, that is, $n(n-1) / 2$. Suppose the lowest scoring team ends with $k$ points. Then the total score for all teams is
$$
k+(k+1)+\cdots+(k+n-1)=n k+\frac{(n-1) n}{2}
$$
Some games must end in a tie, for otherwise, all team scores would be a multiple of 3 and cannot be 1 point apart. Since the total score of a tie is only 2 points compared to 3 points if one of the teams wins, we therefore know that
$$
n k+\frac{(n-1) n}{2}<3 \cdot \frac{n(n-1)}{2}
$$
so $n k<n(n-1)$, and hence $k<n-1$. It follows that the lowest scoring team can score no more than $n-2$ points.
We now show by induction that it is indeed possible for the lowest scoring team to score $n-2$ points.
The following scoreboard shows this is possible for $n=4$ :
| - | 3 | 1 | 1 | 5 |
| :---: | :---: | :---: | :---: | :---: |
| 0 | - | 1 | 3 | 4 |
| 1 | 1 | - | 1 | 3 |
| 1 | 0 | 1 | - | 2 |
Now suppose we have a scoreboard for $n$ teams labelled $T_{n-2}, \ldots, T_{2 n-3}$, where team $T_{i}$ scores $i$ points. Keep the results among these teams unchanged while adding one more team.
Write $n=3 q+r$ with $r \in\{1,-1,0\}$, and let the new team tie with just one of the original teams, lose against $q$ teams, and win against the rest of them. The new team thus wins $n-1-q$ games, and gets $1+3(n-1-q)=3 n-2-3 q=2 n-2+r$ points.
Moreover, we arrange for the $q$ teams which win against the new team to form an arithmetic sequence $T_{j}, T_{j+3}, \ldots, T_{j+3(q-1)}=T_{j+n-r-3}$, so that each of them, itself having gained three points, fills the slot vacated by the next one.
(i) If $r=1$, then let the new team tie with team $T_{n-2}$ and lose to each of the teams $T_{n-1}, T_{n+2}, \ldots, T_{n-1+n-r-3}=T_{2 n-5}$.
Team $T_{n-2}$ now has $n-1$ points and takes the place vacated by $T_{n-1}$. At the other end, $T_{2 n-5}$ now has $2 n-2$ points, just one more than the previous top team $T_{2 n-3}$. And the new team has $2 n-2+r=2 n-1$ points, becoming the new top team. The teams now have all scores from $n-1$ up to $2 n-1$.
(ii) If $r=-1$, then let the new team tie with team $T_{2 n-3}$ and lose to each of the teams $T_{n-2}, T_{n+1}, \ldots, T_{n-2+n-r-3}=T_{2 n-4}$.
The old top team $T_{2 n-3}$ now has $2 n-2$ points, and its former place is filled by the new team, which gets $2 n-2+r=2 n-3$ points. $T_{2 n-4}$ now has $2 n-1$ points and is the new top team. So again we have all scores ranging from $n-1$ up to $2 n-1$.
(iii) If $r=0$, then let the new team tie with team $T_{n-2}$ and lose to teams $T_{n-1}, T_{n+2}, \ldots, T_{n-1+n-r-3}=T_{2 n-4}$.
Team $T_{n-2}$ now has $n-1$ points and fills the slot vacated by $T_{n-1}$. At the top end, $T_{2 n-4}$ now has $2 n-1$ points, while the new team has $2 n-2+r=2 n-2$ points, and yet again we have all scores from $n-1$ to $2 n-1$.
This concludes the proof.
| n-2 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
LIV OM - II - Task 3
Given is the polynomial $ W(x) = x^4 - 3x^3 + 5x^2 - 9x $. Determine all pairs of different integers $ a $, $ b $ satisfying the equation | Notice that $ W(x) = (x - 1)(x - 2)(x^2 + 3) - 6 $. For $ n > 3 $, the following inequalities therefore hold
and moreover
From this, we obtain
Thus, the values of the polynomial $ W $ at the points $ -2, \pm 3, \pm 4, \ldots $ are pairwise distinct. We directly calculate that
and from inequality (1), we conclude that the values of the polynomial $ W $ at the remaining integer points are greater than $ W(3) = 18 $. Therefore, we obtain a total of four pairs of numbers satisfying the conditions of the problem:
(Note: The specific inequalities and calculations are not provided in the original text, so they are left as blank spaces in the translation.) | (-1,0),(0,-1),(1,2),(2,1) | Algebra | math-word-problem | Yes | Yes | olympiads | false |
XXIV OM - I - Problem 8
Find a polynomial with integer coefficients of the lowest possible degree, for which $ \sqrt{2} + \sqrt{3} $ is a root. | We will find a polynomial with integer coefficients, of which the root is the number $ a = \sqrt{2} + \sqrt{3} $. It is, of course, a root of the polynomial
This polynomial, however, does not have integer coefficients. Let's multiply the polynomial (1) by $ x - \sqrt{2} + \sqrt{3} $. We get $ (x - \sqrt{2})^2 - 3 $, that is,
Of course, the number $ \alpha $ is a root of the polynomial (2). However, not all of its coefficients are integers. Let's then multiply the polynomial (2) by $ x^2 + 2\sqrt{2}x - 1 $. We get,
The number $ \alpha $ is a root of the polynomial (3), which has integer coefficients.
We will prove that (3) is the polynomial of the lowest degree among such polynomials with integer coefficients, of which the root is the number $ \alpha $.
First, we will show that the polynomial (3) is not the product of two polynomials of positive degree with rational coefficients. If the polynomial (3) were divisible by a polynomial of the first degree with rational coefficients, then it would have a root in the set of rational numbers. Any such root is an integer that divides the constant term of the polynomial (3). It is easy to check that neither $ 1 $ nor $ - 1 $ is a root of this polynomial.
Next, we will prove that the polynomial (3) is not divisible by any quadratic polynomial with rational coefficients. If,
where $ a, b, c, d \in \mathbb{Q} $, then by comparing the coefficients of the same powers of $ x $ on both sides of equation (7), we would get the system of equations,
Solving for $ c $ from the first equation and for $ d $ from the last equation, and substituting into the remaining equations, we get,
Hence, $ a = 0 $, or $ b = \pm 1 $.
If $ a = 0 $, then $ b + \frac{1}{b} = - 10 $, that is, $ b^2 - 10 b + 1 = 0 $. This last equation has no roots in the set of rational numbers.
If $ b = 1 $, then $ a^2 = 12 $, and if $ b = - 1 $, then $ a^2 = 8 $. In neither of these cases is $ a $ a rational number.
If the number $ \sqrt{2} + \sqrt{3} $ were a root of some non-zero polynomial $ f $ of degree at most three with rational coefficients and this degree were minimal, then denoting by $ g $ and $ r $ the quotient and remainder of the division of the polynomial (3) by $ f $, we would get,
where $ \mathrm{deg} \, r < \mathrm{deg} \, f $. Here, $ r $ is not the zero polynomial, since, as we have shown, the polynomial (3) is not the product of two polynomials of positive degree with rational coefficients.
Substituting $ x = \sqrt{2} + \sqrt{3} $ in the last equation, we get $ r( \sqrt{2} + \sqrt{3}) = 0 $. However, the polynomial $ f $ had the smallest degree among non-zero polynomials with rational coefficients, of which the root is the number $ \sqrt{2} + \sqrt{3} $. Since $ \mathrm{deg} \, r < \mathrm{deg} \, f $, we have reached a contradiction. | x^4-10x^2+1 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
XLVII OM - I - Problem 2
A palindromic number is defined as a natural number whose decimal representation read from left to right is the same as when read from right to left. Let $ (x_n) $ be the increasing sequence of all palindromic numbers. Determine all prime numbers that are divisors of at least one of the differences $ x_{n+1}-x_n $. | The decimal representation of the palindromic number $ x_n $ (respectively: ($ 2m $)-digit or ($ 2m-1 $)-digit) looks like this:
or
($ c_i \in \{ 0,1,2,3,4,5,6,7,8,9\} $ for $ i = 1, \ldots ,m;\ c_1 \ne 0 $). There are three possible situations:
Case I. $ c_m \ne 9 $. If $ x_n $ has the form (1), then $ x_{n+1} $ (the smallest palindromic number greater than $ x_n $) has the decimal representation
where $ d_m = c_m + 1 $.
Justification: Example (3) shows that there are palindromic numbers greater than $ x_n $ and having the same initial digits $ c_1,c_2,\ldots,c_{m-1} $ as $ x_n $; thus, $ x_{n+1} $ must be one of these numbers. Its next ($ m $-th) digit cannot be $ c_m $, because then the number would be identical to $ x_n $ (formula (1)). By taking $ d_m= c_m +1 $ as the next digit, we get the only palindromic number with the initial digits $ c_1,c_2,\ldots,c_{m-1},d_m $ (its further digits are already uniquely determined; see formula (3)); and by writing any digit greater than $ d_m $ on the $ m $-th place, we get even larger numbers; therefore, formula (3) indeed represents the number $ x_{n+1} $.
Analogous reasoning shows that if $ x_n $ has the form (2), then $ x_{n+1} $ has the decimal representation
where $ d_m = c_m + 1 $.
We calculate the difference $ x_{n+1} -x_n $ using the usual subtraction algorithm (that is, by writing the digits of the number $ x_n $ under the corresponding digits of the number $ x_{n+1} $ and performing "written subtraction"). The result of the subtraction:
Case II. Not all digits of the number $ x_n $ (given by formula (1) or (2)) are nines, but the digit $ c_m $ is a nine: $ c_m = 9 $. Let $ c_k $ be the last digit different from $ 9 $ in the sequence $ c_1,c_2,\ldots,c_{m-1},c_m $. Then
where $ l = 2m-2k $ or $ l = 2m-1-2k $, depending on whether the number $ x_n $ is expressed by formula (1) or (2). In each of these cases, the smallest palindromic number greater than $ x_n $ has the representation
where $ d_k = c_k + 1 $. (Detailed justification - very similar to the one conducted in Case I.) The subtraction algorithm now gives the result
Case III. All digits of the number $ x_n $ are nines:
Then $ x_{n+1} = \overline{1 \underbrace{00\ldots 0}_{p-1}1} $, so
Cases I, II, III exhaust all possibilities. The results obtained in formulas (5), (6), (7) show that the only prime divisors of the differences $ x_{n+1}-x_n $ are the numbers $ 2 $, $ 5 $, and $ 11 $. | 2,5,11 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
VI OM - I - Problem 9
Present the polynomial $ x^4 + x^3 + x^2 + x + 1 $ as the difference of squares of two polynomials of different degrees with real coefficients. | If the polynomial $ W (x) = x^4 + x^3 + x^2 + x + 1 $ is equal to the difference $ U(x)^2 - V(x)^2 $, where $ U(x) $ and $ V(x) $ are polynomials of different degrees, then the polynomial $ U(x) $ must be of the second degree and the polynomial $ V(x) $ must be of the first or zero degree. In this case, the polynomial $ V(x)^2 $ does not contain terms of degree higher than two, so the first two terms of the polynomial $ U(x)^2 $ must be the same as in the given polynomial $ W(x) $, i.e., $ U(x)^2 $ has the form $ x^4 + x^3 + \ldots $. From this, we conclude that the polynomial $ U(x) $ has the form $ U(x) = x^2 + \frac{1}{2}x + a $. Therefore,
From the expression obtained for $ V(x)^2 $, we see that $ V(x) $ cannot be of zero degree, as it cannot be simultaneously $ 2a - \frac{3}{4} = 0 $ and $ a - 1 = 0 $; $ V(x) $ must therefore be of the first degree. It follows further that the square of the function $ V(x) $ must be a quadratic trinomial, in which the coefficient of $ x^2 $ is positive, and the discriminant equals $ 0 $, thus
The second condition gives, after simplification, the equation
This equation has three roots $ a = 1 $ and $ a = \frac{1}{4} $ ($ -1 \pm \sqrt{5} $), of which only the root $ a = 1 $ satisfies the condition $ 2a - \frac{3}{4} > 0 $. Ultimately, we obtain the factorization
as the only solution to the problem. | x^4+x^3+x^2+x+1=(x^2+\frac{1}{2}x+1)^2-(\frac{1}{2}x)^2 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
XLVI OM - I - Problem 11
Given are natural numbers $ n > m > 1 $. From the set $ \{1,2, \ldots ,n\} $, we draw $ m $ numbers without replacement. Calculate the expected value of the difference between the largest and the smallest drawn number. | An elementary event is the selection of an $m$-element subset from an $n$-element set. These elementary events are equally probable; there are $ {n}\choose{m} $ of them. Let the largest and smallest selected number be denoted by $a$ and $b$, respectively. The random variable $X$ under consideration, which is the difference $a - b$, can take any integer value from $m - 1$ to $n - 1$.
Let us fix a natural number $r$ satisfying the inequalities $m - 1 \leq r \leq n - 1$. In the set $\{1, 2, \ldots, n\}$, there are $n - r$ pairs of numbers $a$, $b$ with the difference $a - b = r$. For a fixed position of the numbers $a$ and $b$, there are $ {r-1}\choose{m-2} $ ways to choose the remaining $m-2$ numbers from the set $\{b+1, \ldots, a-1\}$. Therefore, the product $(n - r) {{r-1}\choose{m-2}}$ represents the number of $m$-element subsets of the set $\{1, 2, \ldots, n\}$ in which the difference between the largest and smallest element is $r$—that is, the number of elementary events in which the random variable $X$ takes the value $r$.
Dividing this product by the number of all elementary events gives the probability that $X = r$; let us denote this probability by $p_r$. Thus,
\[
p_r = \frac{(n - r) {{r-1}\choose{m-2}}}{{n}\choose{m}}
\]
Using the easily justified relationships
\[
{n \choose m} = \frac{n!}{m!(n-m)!} \quad \text{and} \quad {r-1 \choose m-2} = \frac{(r-1)!}{(m-2)!(r-m+1)!}
\]
we transform the obtained expression as follows:
\[
p_r = \frac{(n - r) \frac{(r-1)!}{(m-2)!(r-m+1)!}}{\frac{n!}{m!(n-m)!}} = \frac{(n - r) (r-1)! m! (n-m)!}{(m-2)! (r-m+1)! n!}
\]
Since $r$ takes values from $m-1$ to $n-1$, the expected value of the random variable $X$, which is the number
\[
E(X) = \sum_{r=m-1}^{n-1} r p_r
\]
is equal to
\[
E(X) = \sum_{r=m-1}^{n-1} r \frac{(n - r) (r-1)! m! (n-m)!}{(m-2)! (r-m+1)! n!}
\]
To simplify the sums in the square brackets, we use the formula
\[
\sum_{r=j}^{N} {r \choose j} = {N+1 \choose j+1}
\]
(see: Note). By setting $N = n - 1$ and $j = m - 1$ in this formula, and then $N = n$ and $j = m$, we obtain, respectively:
\[
\sum_{r=m-1}^{n-1} {r \choose m-1} = {n \choose m}
\]
and
\[
\sum_{r=m}^{n} {r \choose m} = {n+1 \choose m+1}
\]
(applying a change of the summation index: $s = r + 1$). We can now complete the calculation (1):
\[
E(X) = \sum_{r=m-1}^{n-1} r \frac{(n - r) (r-1)! m! (n-m)!}{(m-2)! (r-m+1)! n!} = \frac{m(n-1)}{n-m+1}
\]
This is the sought value.
Note. Formula (2) is well-known. It can be easily proven by induction on $N$ for a fixed $j$. It can also be "seen" by carefully examining Pascal's triangle; we recommend this as a pleasant exercise in observation for the readers. | \frac{(n-1)}{n-+1} | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Given an integer $ c \geq 1 $. To each subset $ A $ of the set $ \{1,2, \ldots ,n\} $, we assign a number $ w(A) $ from the set $ \{1,2, \ldots ,c\} $ such that the following condition is satisfied:
Let $ a(n) $ be the number of such assignments. Calculate $ \lim_{n\to \infty}\sqrt[n]{a(n)} $.
Note: $ \min(x,y) $ is the smaller of the numbers $ x $, $ y $. | Let $ M $ be the set $ \{1,2,\ldots,n\} $, and $ M_i $ be the $(n-1)$-element set obtained from $ M $ by removing the number $ i $:
Given the assignment as mentioned in the problem, let's denote the value $ w(M) $ by $ m $, and the value $ w(M_i) $ by $ f(i) $ (for $ i = 1,2, \ldots ,n $). According to the conditions of the problem, the values $ f(1), \ldots ,f(n) $ and $ m $ are numbers from the set $ \{1,2, \ldots ,c\} $, and for each $ i $, the following equality holds:
This is simply a fancy way of writing the inequality:
Thus, the assignment $ w(\cdot) $ is associated with the function:
From the condition imposed on the assignment $ w(\cdot) $:
it follows by induction that the equality:
holds for any sets $ A_1,\ldots,A_k $ contained in $ M $. (The symbol $ \min(x_1,\ldots,x_k) $ denotes the smallest of the numbers $ x_1,\ldots,x_k $; it can, of course, be the common value of several of these numbers.)
Let $ A $ be any subset of the set $ M $, not identical to the entire set $ M $, and let $ i_1,\ldots,i_k $ be all the numbers in $ M $ that do {\it not} belong to $ A $:
The set $ A $ is then exactly the intersection of the sets $ M_{i_1},\ldots,M_{i_k} $:
Indeed: a number $ i $ belongs simultaneously to all sets $ M_{i_1},\ldots,M_{i_k} $ if and only if it belongs to $ M $ and is different from the numbers $ i_1,\ldots,i_k $ - that is, (in accordance with (3)) if and only if it is an element of the set $ A $.
From the connections (4), (2), (3), the equality follows:
(The symbol $ \min_{i \not \in A}f(i) $ denotes the minimum value taken by the function $ f $ on those elements of the set $ M $ that do not belong to the set $ A $.)
Conclusion: the assignment $ w(\cdot) $ is fully determined by specifying the value $ m = w(M) $ and the values $ f(i) = w(M_i) $ for $ i = 1,2,\ldots ,n $. In other words, it is determined by choosing the number $ m $ and the function (1); it is then given by the formula:
And conversely: if $ m $ is any positive integer not exceeding $ c $, and if $ f $ is any mapping of the set $ M $ into the set $ \{1,2,\ldots,m\} $, then the formula (5) defines an assignment $ A \mapsto w(A) $ satisfying the condition stated in the problem.
For a fixed $ m $, there are exactly $ m^n $ functions (1). Therefore, the number of admissible assignments (5) is:
We obtain the two-sided estimate $ c^n \leq a(n) \leq c^n \cdot c $; and hence:
As $ n $ approaches infinity, the $ n $-th root of any fixed positive number approaches $ 1 $. Therefore, the expression on the right side of the inequality (6) approaches $ c $, and by the squeeze theorem, $ \displaystyle \lim_{n \to \infty} \sqrt[n]{a(n)} = c $.
The answer is: The sought limit value is the number $ c $. | c | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
LV OM - III - Task 3
In a certain tournament, $ n $ players participated $ (n \geq 3) $. Each played against each other exactly once, and there were no draws. A three-element set of players is called a draw triplet if the players can be numbered in such a way that the first won against the second, the second against the third, and the third against the first. Determine the maximum number of draw triplets that could have appeared in the tournament. | Instead of determining the maximum number of draw triples, we will determine the minimum number of non-draw triples.
Let's number the players from 1 to $ n $ and assume that player number $ i $ won $ x_i $ times. Then the total number of matches is
Each non-draw triple is uniquely determined by the player who won against the other two players in that triple. Therefore, player number $ i $ determines $ x_i \choose 2 $ non-draw triples, and the total number of non-draw triples in the tournament is
In the further part of the solution, we will consider two cases:
The number $ n $ is odd, i.e., $ n = 2k + 1 $. Then, by the inequality between the quadratic mean and the arithmetic mean, we obtain
Thus, the number of draw triples does not exceed
The above number of draw triples will occur only when each player wins exactly $ k $ times (equality holds in inequality (1) at that time). Such a result of the matches can be achieved in the following way. We seat the players around a round table and assume that each of them won only against the players sitting to their right at a distance of no more than $ k $ places. In such a setup of matches, each player won exactly $ k $ times.
The number $ n $ is even, i.e., $ n = 2k $. Then $ (x_i - k)(x_i - k + 1) \geq 0 $ for $ i = 1,2,\ldots,n $, from which we obtain $ x_i^2 \geq (2k - 1)x_i - k(k - 1) $. Therefore,
From this, it follows that the number of draw triples does not exceed
The above number of draw triples will occur only when each player wins $ k $ or $ k-1 $ times (equality holds in inequality (2) at that time). Such a result of the matches can be achieved in the following way. As above, we seat the players around a round table and assume that each of them won against the players sitting to their right at a distance of no more than $ k-1 $ places. The result of the match between players sitting opposite each other is determined arbitrarily. In this way, each player won $ k $ or $ k-1 $ times.
Summarizing: the maximum number of draw triples that can appear in the tournament is $ \frac{1}{24}n(n^2 - 1) $ if $ n $ is an odd number, and $ \frac{1}{24}n(n^2 - 4) $ if $ n $ is an even number. | \frac{1}{24}n(n^2-1) | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
XXIV OM - I - Problem 10
Find the smallest natural number $ n > 1 $ with the following property: there exists a set $ Z $ consisting of $ n $ points in the plane such that every line $ AB $ ($ A, B \in Z $) is parallel to some other line $ CD $ ($ C, D \in Z $). | We will first prove that the set $ Z $ of vertices of a regular pentagon has the property given in the problem, that is, $ n \leq 5 $. We will show that each side of the regular pentagon is parallel to a certain diagonal and vice versa, each diagonal is parallel to a corresponding side.
It suffices to prove that $ AB \parallel CE $ (Fig. 11). Since a circle can be circumscribed around quadrilateral $ ABCE $ (namely, it is the circle circumscribed around the given regular pentagon), we have $ \measuredangle A + \measuredangle BCE = \pi $. Since $ \measuredangle A = \measuredangle B $, it follows that $ \measuredangle BCE = \pi - \measuredangle B $, which proves that $ AB \parallel CE $.
On the other hand, from the conditions of the problem, it follows that $ n \geq 4 $, since there are at least two different parallel lines, each containing at least two points of the set $ Z $. If $ n = 4 $ and points $ A, B, C, D $ satisfied the conditions of the problem, they would be the vertices of a trapezoid. However, none of the diagonals of a trapezoid is parallel to another line determined by its vertices. Therefore, $ n > 4 $, and from the previously proven inequality $ n \leq 5 $, it follows that $ n = 5 $. | 5 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
XXV - I - Task 1
During World War I, a battle took place near a certain castle. One of the shells destroyed a statue of a knight with a spear standing at the entrance to the castle. This happened on the last day of the month. The product of the day of the month, the month number, the length of the spear expressed in feet, half the age of the battery commander firing at the castle expressed in years, and half the time the statue stood expressed in years equals 451,066. In which year was the statue erected? | The last day of the month can only be $28$, $29$, $30$, or $31$. Of these numbers, only $29$ is a divisor of the number $451,066 = 2 \cdot 7 \cdot 11 \cdot 29 \cdot 101$. Therefore, the battle took place on February $29$ in a leap year. During World War I, only the year $1916$ was a leap year. From the problem statement, it follows that a divisor of the number $7 \cdot 11 \cdot 101$ is half the age of the battery commander. Only the number $11$ satisfies this condition, so the battery commander was $22$ years old. The length of the pike is a divisor of the number $7 \cdot 101$. Therefore, the pike was $7$ feet long. Thus, half the time the statue stood is $101$ years. It was erected $202$ years before the year $1916$, i.e., in the year $1714$. | 1714 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
XXI OM - III - Task 1
Diameter $ \overline{AB} $ divides the circle into two semicircles. On one semicircle, n points $ P_1 P_2, \ldots, P_n $ are chosen such that $ P_1 $ lies between $ A $ and $ P_2 $, $ P_2 $ lies between $ P_1 $ and $ P_3 $, $ \ldots $, $ P_n $ lies between $ P_{n-1} $ and $ B $. How should point $ C $ be chosen on the other semicircle so that the sum of the areas of triangles $ CP_1P_2, CP_2P_3, CP_3P_4, \ldots, CP_{n-1}P_n $ is maximized? | Notice that the sum of the areas of triangles $ CP_1P_2, CP_2P_3, CP_3P_4, \ldots, CP_{n-1}P_n $ is equal to the sum of the areas of the polygon $ P_1P_2 \ldots P_n $ and triangle $ CP_1P_n $ (Fig. 13). The first area does not depend on the choice of point $ C $. The second area will be maximal when the distance from point $ C $ to the line $ P_1P_n $ is as large as possible. The point on the circle farthest from a given chord lies on the perpendicular bisector of that chord. Therefore, $ C $ should be the point of intersection of the perpendicular bisector of segment $ \overline{P_1P_n} $ with the other semicircle. | C | Geometry | math-word-problem | Yes | Yes | olympiads | false |
LVI OM - I - Problem 10
Among all subsets of a fixed $ n $-element set $ X $, we sequentially draw with replacement three sets $ A $, $ B $, $ C $. Each time, the probability of drawing any of the $ 2^n $ subsets of set $ X $ is equally likely. Determine the most probable number of elements in the set $ A\cap B\cap C $. | The set of elementary events $\Omega$ consists of all triples $(A,B,C)$, where $A$, $B$, and $C$ are subsets of a given $n$-element set $S$. The selection of each of the $(2^n)^3 = 8^n$ triples $(A,B,C)$ is equally probable. Let $X_k$ $(k = 0,1,2,\ldots,n)$ denote the event that the triple of sets $(A,B,C)$ satisfies the condition $|A \cap B \cap C| = k$, where $|F|$ denotes the number of elements in the set $F$. We seek the natural number $k$ for which the probability of the event $X_k$ is the greatest.
Let us fix a number $k \in \{0,1,2, \ldots,n\}$. We will calculate the number of triples $(A, B, C)$ for which $|A \cap B \cap C| = k$.
If $(A,B,C)$ is a triple of subsets of the set $S$, then each element of the set $S$ is in exactly one of the following eight sets
In order to obtain a triple of sets $(A, B, C)$ for which $|A \cap B \cap C| = k$, we first choose $k$ elements of the set $S$ to place in the set $A \cap B \cap C$ — this can be done in $n \choose k$ ways. Each of the remaining $n-k$ elements of $k$ is assigned one of the remaining seven possibilities listed in (1) — this can be done in $7^{n-k}$ ways. The described procedure uniquely determines the triple $(A,B,C)$. Therefore, the number of triples $(A,B,C)$ for which $|A \cap B \cap C| = k$ is ${n \choose k} \cdot 7^{n-k}$. Hence, we obtain
To determine the number $k$ for which the probability of the event $X_k$ is the greatest, we calculate the ratio
From this, it follows that
Denoting $\lambda = [(n-7)/8]$, where $[x]$ is the greatest integer not greater than $x$, we obtain
Thus, the probability $P(X_k)$ is the greatest for $k = \lambda + 1 = [\frac{1}{8} (n+1)]$.
If $\frac{1}{8}(n-7)$ is an integer, then there are two values of $k$ for which the number $P(X_k)$ is the greatest, namely $k = \frac{1}{8} (n-7)$ and $k = \frac{1}{8} (n+1)$. | [\frac{1}{8}(n+1)] | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
XXII OM - I - Problem 10
Given is a table with $ n $ rows and $ n $ columns. The number located in the $ m $-th column and $ k $-th row is equal to $ n(k - 1) + m $. How should $ n $ numbers be chosen, one from each row and each column, so that the product of these numbers is the largest? | Let's denote $ a_{k,m} = n (k - 1) + m $, where $ 1 \leq k, m \leq n $. Suppose we select the number in the column with number $ m_i $ from the $ i $-th row, where $ i = 1, 2, \ldots, n $. From the conditions of the problem, it follows that the sequence $ m_1, m_2, \ldots, m_n $ has distinct terms. Each such sequence corresponds to the product $ a_{1m_1} \cdot a_{2m_2} \cdot \ldots \cdot a_{nm_n} $.
We will prove that if the sequence $ m_1, m_2, \ldots, m_n $ is not decreasing, then the corresponding product is not the largest.
For example, let $ m_i < m_{i+1} $ for some $ i $. Consider the products $ A $ and $ B $ corresponding to the sequences:
and
(these sequences differ only in the terms with numbers $ i $ and $ i + 1 $). Therefore,
and
Let $ \displaystyle C= \prod_{k \ne i, i+1} a_{km_k} $ and using the definition of the numbers $ a_{km} $, we get:
Thus, $ B > A $, which means the product corresponding to the second sequence is greater than the product corresponding to the first. Therefore, we have proven that if the sequence $ m_1, m_2, \ldots, m_n $ is not decreasing, then the corresponding product is not the largest. Hence, the largest product corresponds to a decreasing sequence. Since from the numbers $ 1, 2, \ldots, n $, we can form only one $ n $-term decreasing sequence, namely the sequence $ n, n - 1, \ldots, 2, 1 $, the largest product is equal to $ a_{1n}a_{2n-1} \ldots a_{n1} = n(2n - 1) (3n - 2) (4n - 3) \ldots (n^2 - (n -1)) $. | a_{1n}a_{2n-1}\ldotsa_{n1}=n(2n-1)(3n-2)(4n-3)\ldots(n^2-(n-1)) | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
V OM - I - Problem 7
In the plane, a line $ p $ and points $ A $ and $ B $ are given. Find a point $ M $ on the line $ p $ such that the sum of the squares $ AM^2 + BM^2 $ is minimized. | The geometric locus of points $ X $ in the plane for which $ AX^2 + BX^2 $ has a given value $ 2k^2 $ is a certain circle whose center lies at the midpoint $ S $ of segment $ AB $; the radius of this circle is larger the larger $ k $ is.
The smallest circle centered at $ S $ that intersects a line $ p $ is the circle tangent to line $ p $; the point of tangency is the projection $ M $ of point $ S $ onto line $ p $. Point $ M $ is the sought point; the problem always has a solution and only one.
Note. The theorem about the geometric locus, which we referred to in the above solution, can be proven as follows. Let $ AB = c $ and let $ X $ be any point in the plane (Fig. 22). Then
When $ X $ lies outside the line $ AB $, this equality is a known formula for the square of the median of a triangle (see problem 2). When $ X $ lies on the line $ AB $, verifying the equality is easy and is left to the reader.
From this equality, it follows: 1°) if $ AX^2 + BX^2 $ has a given value $ 2k^2 $, then point $ X $ lies on a circle centered at $ S $ with radius $ \sqrt{k^2 - \frac{1}{4} c^2} $; thus, $ k \geq \frac{1}{2} c $, and when $ k = \frac{1}{2} c $, the circle reduces to point $ S $; 2°) if point $ X $ lies on such a circle, i.e., if $ SX = \sqrt{k^2 - \frac{1}{4} c^2} $, then $ AX^2 + BX^2 = 2k^2 $, Q.E.D. | M | Geometry | math-word-problem | Yes | Yes | olympiads | false |
XXIX OM - I - Problem 12
Determine the least upper bound of such numbers $ \alpha \leq \frac{\pi}{2} $, that every acute angle $ MON $ of measure $ \alpha $ and every triangle $ T $ on the plane have the following property. There exists a triangle $ ABC $ isometric to $ T $ such that the side $ \overline{AB} $ is parallel to $ OM $ and the lines perpendicular to $ ON $ and passing through the centroids of triangles $ ABC $ and $ ABC' $ respectively intersect the segment $ \overline{AB} $; $ C' $ is the reflection of vertex $ C $ across the perpendicular bisector of side $ \overline{AB} $.
Note. Physically, the problem means: What should be the angle of inclination of an inclined plane so that for any triangle, one can choose a certain side such that the triangle, placed with this side on the inclined plane, will not tip over. | First, note that if $Q$ is the midpoint of side $\widehat{AC}$, then $\measuredangle ABQ \leq \frac{\pi}{6}$. Indeed, denoting by $D$ the projection of point $A$ onto the line $BQ$, we get $AD \leq AQ = \frac{1}{2} AC \leq \frac{1}{2} AB$ (Fig. 9).
Therefore, $\sin \measuredangle ABQ = \frac{AD}{AB} \leq \frac{1}{2}$. Since angle $ABC$ is not the largest angle of triangle $ABC$, it is acute. Hence, angle $ABQ$ is also acute. From the inequality $\sin \measuredangle ABQ \leq \frac{1}{2}$, we obtain that $\measuredangle ABQ \leq \frac{\pi}{6}$.
Let $\overline{AB}$ be the longest side of triangle $ABC$ isometric to triangle $T$, let $P$ be the centroid of triangle $ABC$, and $P$ be the centroid of triangle $ABC$. We can assume that $A = O$, as this does not change the conditions of the problem (Fig. 10).
om29_1r_img_9.jpgom29_1r_img_10.jpg
From the initial observation, it follows that each of the angles $BOP$ and $BOP$ has a measure not greater than $\frac{\pi}{6}$. Therefore, if $\measuredangle MON \leq \frac{\pi}{3}$, then $\measuredangle NOP = \measuredangle MON + \measuredangle BOP \leq \frac{\pi}{2}$ and similarly $\measuredangle NOP \leq \frac{\pi}{2}$. It follows that the lines perpendicular to $ON$ and passing through points $P$ and $P$ respectively intersect the segment $\overline{AB}$. Therefore, the sought upper bound of the numbers $\alpha$ is not less than $\frac{\pi}{3}$.
Conversely, if the line perpendicular to $ON$ passing through point $P$ intersects the segment $\overline{AB}$, then $\measuredangle NOP \leq \frac{\pi}{2}$. Therefore, $\measuredangle MON = \measuredangle NOP - \measuredangle BOP \leq \frac{\pi}{2} - \measuredangle BOP$. In particular, if $T$ is an equilateral triangle, then $\measuredangle BOP = \frac{\pi}{6}$ and hence
$\measuredangle MON \leq \frac{\pi}{2} - \frac{\pi}{6} = \frac{\pi}{3}$. It follows that the sought upper bound of the numbers $\alpha$ is the number $\frac{\pi}{3}$. | \frac{\pi}{3} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
LVII OM - I - Problem 4
Participants in a mathematics competition solved six problems, each graded with one of the scores 6, 5, 2, 0. It turned out that
for every pair of participants $ A, B $, there are two problems such that in each of them $ A $ received a different score than $ B $.
Determine the maximum number of participants for which such a situation is possible. | We will show that the largest number of participants for which such a situation is possible is 1024. We will continue to assume that the permissible ratings are the numbers 0, 1, 2, 3 (instead of 5 points, we give 4, and then divide each rating by 2).
Let $ P = \{0,1,2,3\} $ and consider the set
Set $ X $ obviously has 4096 elements. We will consider subsets $ A $ of set $ X $ with the following property (*):
(*) If $ (a_1,a_2,\dots,a_6) $, $ (b_1,b_2,\dots,b_6) \in A $, then there exist $i, j$ such that
It suffices to show that the largest number of elements in set $ A $ with property (*) is 1024.
First, we show that if set $ A $ has property (*), then it has at most 1024 elements. Assume, therefore, that we have a subset $ A $ of set $ X $ with property (*) and suppose that it has at least 1025 elements. Since there are exactly 1024 sequences of length 5 with terms from the four-element set $ P $, it follows from the pigeonhole principle that in set $ A $ there are at least two sequences that have the same terms from the first to the fifth. These sequences differ, therefore, only in one term—the sixth, which contradicts property (*). Therefore, set $ A $ has at most 1024 elements.
Now we show that there exists a set $ A $ with at least 1024 elements and having property (*). It suffices to take the following set:
First, we show that set $ A $ has at least 1024 elements. Take any numbers $ a_1,a_2,\dots,a_5 \in P $. We can make such a choice in 1024 ways. Let $ r $ be the remainder of the division of the sum $ a_1+a_2+\dots+a_5 $ by 4, and let $ a_6 = 4 - r $. Then, of course, $ (a_1,a_2,\dots,a_6) \in A $, so we have indicated at least 1024 different sequences in set $ A $.
Finally, we show that set $ A $ has property (*). Suppose that
and sequences $ (a_1,a_2,\dots,a_6) $ and $ (b_1,b_2,\dots,b_6) $ differ in only one term, say the term with index $ k: \; a_k \neq b_k $, where $ 1 \leq k \leq 6 $ and $ a_i = b_i $ for $ i \neq k $. Since the numbers $ a_1 +a_2 +\dots +a_6 $ and $ b_1 +b_2 +\dots+b_6 $ are divisible by 4, their difference is also divisible by 4. But
Thus, the number $ a_k - b_k $ is divisible by 4. Since $ a_k, b_k \in P $, then
In the set $ \{-3,-2, -1,0,1,2,3\} $, there is only one number divisible by 4, namely 0. Therefore, $ a_k = b_k $, contrary to the assumption that sequences $ (a_1,a_2,\dots,a_6) $ and $ (b_1,b_2,\dots,b_6) $ differ in the term with index $ k $. This contradiction proves that set $ A $ has property (*), which completes the proof. | 1024 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
II OM - III - Task 1
A beam of length $ a $ has been suspended horizontally by its ends on two parallel ropes of equal length $ b $. We rotate the beam by an angle $ \varphi $ around a vertical axis passing through the center of the beam. By how much will the beam be raised? | When solving geometric problems, a properly executed drawing is an important aid to our imagination. We represent spatial figures through mappings onto the drawing plane. There are various ways of such mapping. In elementary geometry, we most often draw an oblique parallel projection of the figure; in many cases, it is convenient to use the method of orthogonal projections onto two perpendicular planes, i.e., the so-called Monge's method (compare, for example, problem no. 23 on page 113).
We will present the solution to our problem in two variants, using once one and once the other of the mentioned mapping methods.
When using the method of oblique parallel projection, we will take as the projection plane - the plane passing through the beam $ AB $ and through the suspension points $ M $ and $ N $. We therefore draw the quadrilateral $ ABNM $ "in natural size" (fig. 59 a and b). Let $ S $ denote the midpoint of the beam. After twisting the beam, it will take the position $ CD $. The midpoint of the segment $ CD $ lies on the projection plane; let us assume that this is the point $ T $.
The position of the projection of point $ C $ depends on the direction of projection; for the oblique projection of point $ C $, we can take any point $ C $, for example, as in figure 59 a or 59 b. The projection of point $ D $ will be the point symmetric to point $ C $ with respect to point $ T $.
Calculating the sought length $ ST = x $ is simple. We draw a segment $ TK $ parallel and equal to segment $ SA $; then
So $ AM = b $, and segment $ KM $ is the leg of the right triangle $ KMC $ with the hypotenuse $ MC = b $ and the leg $ KC $. Segment $ KC $ is the base of the isosceles triangle $ KTC $, in which $ TK = TC = \frac{1}{2} AB = \frac{1}{2} a $, $ \measuredangle KTC = \varphi $.
Therefore,
Finally, we get
If $ b < a $, the angle of twist $ \varphi $ cannot be greater than the angle $ \varphi_0 $ given by the formula
For the value $ \varphi = \varphi_0 $, we have $ x = b $. Further increase of the angle is not possible without stretching the lines.
If $ b \geq a $, the maximum value of $ \varphi $ is $ 180^\circ $. For the value $ \varphi = 180^\circ $, the lines cross if $ b > a $, and overlap each other if $ b = a $.
In the above solution, the goal was to calculate the elevation of the beam after its twisting. The figure in parallel projection was only a possibly simple illustration necessary for this calculation. If we want the drawing to be a graphical solution to the problem, i.e., to give the correct length of segment $ ST $ given the lengths $ a $, $ b $, and the angle $ \varphi $, it should be done a bit differently. Specifically, the point $ T $, which we chose arbitrarily in figures 59 a and b, must be constructed from the given quantities $ a $, $ b $, $ \varphi $.
For this purpose, note that in the right triangle $ KMC $, we know the hypotenuse $ MC = MA = b $ and the leg $ KC $, which is the base of the isosceles triangle $ KCT $, where $ TK = TC = \frac{1}{2} a $, and $ \measuredangle KTC = \varphi $. From these data, we can construct the triangle to find the length of $ KM $ and the length of $ ST = AM - KM $.
The construction is shown in figure 60.
We construct triangle $ ASP $, where $ AS = SP = \frac{1}{2}a $, $ \measuredangle ASP = \varphi $. We draw a semicircle with diameter $ AM $ and a chord $ AL = AP $ in it. We measure on the line $ MA $ a segment $ MK $ equal to segment $ ML $. Point $ K $ determines the level of point $ T $; the sought elevation will be determined by segment $ TS = KA $.
The projection of the twisted beam $ C $ will be drawn as before, choosing point $ C $ arbitrarily. | \sqrt{b^2-(\frac{} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
LVII OM - III - Problem 2
Determine all positive integers $ k $ for which the number $ 3^k+5^k $ is a power of an integer with an exponent greater than 1. | If $ k $ is an even number, then the numbers $ 3^k $ and $ 5^k $ are squares of odd numbers, giving a remainder of 1 when divided by 4. Hence, the number $ 3^k + 5^k $ gives a remainder of 2 when divided by 4, and thus is divisible by 2 but not by $ 2^2 $. Such a number cannot be a power of an integer with an exponent greater than 1.
If $ k $ is an odd number, then
The second factor on the right side of the above relationship contains an odd (equal to $ k $) number of odd summands.
Hence, the number $ 3^k + 5^k $ is divisible by 8 and not by 16. If this number is a power of an integer with an exponent greater than 1, then it must be a cube of an integer.
If $ k = 1 $, then the considered number is a cube of an integer: $ 3^1 + 5^1 = 2^3 $. Let us assume in the further part of the reasoning that $ k \geq 3 $. From the relationship
it follows that cubes of integers give remainders of 0, 1, 8 when divided by 9. For $ k \geq 3 $ we have $ 9 | 3^k $, so $ 3^k + 5^k \equiv 5^k (\mod 9) $.
The remainders of the numbers $ 5, 5^2, 5^3, 5^4, 5^5, 5^6 $ when divided by 9 are 5, 7, 8, 4, 2, 1, respectively. Therefore, if $ 3^k + 5^k $ is a cube of an integer for $ k \geq 3 $, then $ 3 | k $. We have previously shown that $ k $ cannot be an even number.
Thus, the number $ k $ is of the form $ 6l + 3 $, where $ l $ is a non-negative integer.
From the relationship $ 3^3 \equiv 5^3 \equiv 6 (\mod 7) $ and $ 3^6 \equiv 5^6 \equiv 1 (\mod 7) $, it follows that
However, from direct verification, we obtain that the cube of an integer gives a remainder of 0, 1, or 6 when divided by 7:
Therefore, the considered number for $ k \geq 3 $ cannot be a cube of an integer, which concludes the solution of the problem.
Answer: $ k = 1 $. | 1 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
XXIV OM - I - Problem 12
In a class of n students, a Secret Santa event was organized. Each student draws the name of the person for whom they are to buy a gift, so student $ A_1 $ buys a gift for student $ A_2 $, $ A_2 $ buys a gift for $ A_3 $, ..., $ A_k $ buys a gift for $ A_1 $, where $ 1 \leq k \leq n $. Assuming that all drawing outcomes are equally probable, calculate the probability that $ k = n $. | In the result of any drawing, each student draws a certain student from the same class (possibly themselves), and different students draw different students. Therefore, the result of each drawing defines a certain one-to-one mapping (permutation) of the set of all students in the class onto itself. Conversely, each permutation can be the result of some drawing. Therefore, the number of elementary events is equal to the number of permutations of an $n$-element set, i.e., $n!$.
The favorable event will occur when a certain student $A_1$ draws one of the remaining $n-1$ students, denoted by $A_2$; student $A_2$ draws one of the $n-2$ students different from $A_1$ and $A_2$, denoted by $A_3$; $\ldots$; finally, student $A_{n-1}$ draws student $A_n$ different from $A_1, A_2, \ldots, A_{n-1}$. Since student $A_1$ can draw a student different from themselves in $n-1$ ways, student $A_2$ can draw a student different from $A_1$ and $A_2$ in $n-2$ ways, etc., the number of favorable events is equal to $(n-1)(n-2) \ldots 2 \cdot 1 = (n-1)!$.
Therefore, the probability that $k = n$ is $\displaystyle \frac{(n-1)!}{n!} = \frac{1}{n}$. | \frac{1}{n} | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
VIII OM - I - Task 6
Find a four-digit number, whose first two digits are the same, the last two digits are the same, and which is a square of an integer. | If $ x $ is the number sought, then
where $ a $ and $ b $ are integers satisfying the inequalities $ 0 < a \leq 9 $, $ 0 \leq b \leq 9 $. The number $ x $ is divisible by $ 11 $, since
Since $ x $ is a perfect square, being divisible by $ 11 $ it must be divisible by $ 11^2 $, so the number
is divisible by $ 11 $. It follows that $ a + b $ is divisible by $ 11 $, and since $ 0 < a + b \leq 18 $, then $ a + b = 11 $. Therefore,
from which we infer that $ 9a + 1 $ is the square of some natural number $ m $:
Since $ 9a + 1 \leq 82 $, then $ m \leq 9 $.
From the above,
It follows from this equality that the product $ (m + 1) (m - 1) $ is divisible by $ 9 $, and since at most one of the numbers $ m + 1 $ and $ m - 1 $ is divisible by $ 3 $, then one of them is divisible by $ 9 $. Considering that the natural number $ m $ is less than $ 10 $, we conclude from this that $ m + 1 = 9 $, so $ m = 8 $. In this case, $ a = 7 $, $ b = 4 $, and the sought number is $ 7744 = (88)^2 $. | 7744 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.