title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python 3 -> 91.11% faster. 52ms time. Explanation added | how-many-numbers-are-smaller-than-the-current-number | 0 | 1 | **Suggestions to make it better are always welcomed.**\n\n**2 possible solutions:**\n1. For every i element, iterate the list with j as index. If i!=j and nums[j]<nums[i], we can update the count for that number. Time: O(n2). Space: O(1)\n2. This is optimal solution. We can sort the list and store in another temp list. We use dictionary to store the counts and later use it to create result. Time: O(n log n) bcoz of sort. Space: O(n) bcoz of dictionary.\n\n**Explanation of solution 2:**\nnums = 8, 1, 2, 2, 3\n1. We sort the list bcoz we don\'t want to keep traversing the list back and forth. After sorting, we get temp = 1, 2, 2, 3, 8\n2. We traverse temp list. If we find unique element, we know all the previous elements have been recorded. So we add this unique element to the dictionary with index i as value.\nIf duplicate element is encountered, we don\'t add it and don\'t update the value in dictionary.\n3. After the dictionary is constructed, we create output after doing O(1) lookup in dictionary for nums[i]\n\n```\ndef smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:\n\ttemp = sorted(nums)\n\tmapping = {}\n\tresult = []\n\tfor i in range(len(temp)):\n\t\tif temp[i] not in mapping:\n\t\t\tmapping[temp[i]] = i\n\tfor i in range(len(nums)):\n\t\tresult.append(mapping[nums[i]])\n\treturn result\n```\n\n**If this solution helped, please upvote it for others to take advantage of it and learn their techniques** | 201 | You are given an integer array `bloomDay`, an integer `m` and an integer `k`.
You want to make `m` bouquets. To make a bouquet, you need to use `k` **adjacent flowers** from the garden.
The garden consists of `n` flowers, the `ith` flower will bloom in the `bloomDay[i]` and then can be used in **exactly one** bouquet.
Return _the minimum number of days you need to wait to be able to make_ `m` _bouquets from the garden_. If it is impossible to make m bouquets return `-1`.
**Example 1:**
**Input:** bloomDay = \[1,10,3,10,2\], m = 3, k = 1
**Output:** 3
**Explanation:** Let us see what happened in the first three days. x means flower bloomed and \_ means flower did not bloom in the garden.
We need 3 bouquets each should contain 1 flower.
After day 1: \[x, \_, \_, \_, \_\] // we can only make one bouquet.
After day 2: \[x, \_, \_, \_, x\] // we can only make two bouquets.
After day 3: \[x, \_, x, \_, x\] // we can make 3 bouquets. The answer is 3.
**Example 2:**
**Input:** bloomDay = \[1,10,3,10,2\], m = 3, k = 2
**Output:** -1
**Explanation:** We need 3 bouquets each has 2 flowers, that means we need 6 flowers. We only have 5 flowers so it is impossible to get the needed bouquets and we return -1.
**Example 3:**
**Input:** bloomDay = \[7,7,7,7,12,7,7\], m = 2, k = 3
**Output:** 12
**Explanation:** We need 2 bouquets each should have 3 flowers.
Here is the garden after the 7 and 12 days:
After day 7: \[x, x, x, x, \_, x, x\]
We can make one bouquet of the first three flowers that bloomed. We cannot make another bouquet from the last three flowers that bloomed because they are not adjacent.
After day 12: \[x, x, x, x, x, x, x\]
It is obvious that we can make two bouquets in different ways.
**Constraints:**
* `bloomDay.length == n`
* `1 <= n <= 105`
* `1 <= bloomDay[i] <= 109`
* `1 <= m <= 106`
* `1 <= k <= n` | Brute force for each array element. In order to improve the time complexity, we can sort the array and get the answer for each array element. |
Python3 easy solution, Beats 97% | how-many-numbers-are-smaller-than-the-current-number | 0 | 1 | # Intuition\nIf we find a way to not count the duplicates then the index of the numbers when sorted corresponds to the the number of values less than them. so based on this information the solution becomes relatively easy to find\n\n# Approach\nFirst duplicate the array and sort it. then iterate over the sorted duplicate and store the index and the values of the unique values in a dictionary. then apppend the values in the dictionary in the order they come in nums to the result we wish to return.\n\n# Complexity\n- Time complexity:\no(n)\n\n- Space complexity:\no(n)\n\n# Code\n```\nclass Solution:\n def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:\n n = len(nums)\n dup = []\n res = []\n dup = sorted(nums)\n vals = {}\n for i in range(n):\n if dup[i] not in vals:\n vals[dup[i]] = i\n for i in range(n):\n res.append(vals[nums[i]])\n return res\n``` | 4 | Given the array `nums`, for each `nums[i]` find out how many numbers in the array are smaller than it. That is, for each `nums[i]` you have to count the number of valid `j's` such that `j != i` **and** `nums[j] < nums[i]`.
Return the answer in an array.
**Example 1:**
**Input:** nums = \[8,1,2,2,3\]
**Output:** \[4,0,1,1,3\]
**Explanation:**
For nums\[0\]=8 there exist four smaller numbers than it (1, 2, 2 and 3).
For nums\[1\]=1 does not exist any smaller number than it.
For nums\[2\]=2 there exist one smaller number than it (1).
For nums\[3\]=2 there exist one smaller number than it (1).
For nums\[4\]=3 there exist three smaller numbers than it (1, 2 and 2).
**Example 2:**
**Input:** nums = \[6,5,4,8\]
**Output:** \[2,1,0,3\]
**Example 3:**
**Input:** nums = \[7,7,7,7\]
**Output:** \[0,0,0,0\]
**Constraints:**
* `2 <= nums.length <= 500`
* `0 <= nums[i] <= 100` | null |
Python3 easy solution, Beats 97% | how-many-numbers-are-smaller-than-the-current-number | 0 | 1 | # Intuition\nIf we find a way to not count the duplicates then the index of the numbers when sorted corresponds to the the number of values less than them. so based on this information the solution becomes relatively easy to find\n\n# Approach\nFirst duplicate the array and sort it. then iterate over the sorted duplicate and store the index and the values of the unique values in a dictionary. then apppend the values in the dictionary in the order they come in nums to the result we wish to return.\n\n# Complexity\n- Time complexity:\no(n)\n\n- Space complexity:\no(n)\n\n# Code\n```\nclass Solution:\n def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:\n n = len(nums)\n dup = []\n res = []\n dup = sorted(nums)\n vals = {}\n for i in range(n):\n if dup[i] not in vals:\n vals[dup[i]] = i\n for i in range(n):\n res.append(vals[nums[i]])\n return res\n``` | 4 | You are given an integer array `bloomDay`, an integer `m` and an integer `k`.
You want to make `m` bouquets. To make a bouquet, you need to use `k` **adjacent flowers** from the garden.
The garden consists of `n` flowers, the `ith` flower will bloom in the `bloomDay[i]` and then can be used in **exactly one** bouquet.
Return _the minimum number of days you need to wait to be able to make_ `m` _bouquets from the garden_. If it is impossible to make m bouquets return `-1`.
**Example 1:**
**Input:** bloomDay = \[1,10,3,10,2\], m = 3, k = 1
**Output:** 3
**Explanation:** Let us see what happened in the first three days. x means flower bloomed and \_ means flower did not bloom in the garden.
We need 3 bouquets each should contain 1 flower.
After day 1: \[x, \_, \_, \_, \_\] // we can only make one bouquet.
After day 2: \[x, \_, \_, \_, x\] // we can only make two bouquets.
After day 3: \[x, \_, x, \_, x\] // we can make 3 bouquets. The answer is 3.
**Example 2:**
**Input:** bloomDay = \[1,10,3,10,2\], m = 3, k = 2
**Output:** -1
**Explanation:** We need 3 bouquets each has 2 flowers, that means we need 6 flowers. We only have 5 flowers so it is impossible to get the needed bouquets and we return -1.
**Example 3:**
**Input:** bloomDay = \[7,7,7,7,12,7,7\], m = 2, k = 3
**Output:** 12
**Explanation:** We need 2 bouquets each should have 3 flowers.
Here is the garden after the 7 and 12 days:
After day 7: \[x, x, x, x, \_, x, x\]
We can make one bouquet of the first three flowers that bloomed. We cannot make another bouquet from the last three flowers that bloomed because they are not adjacent.
After day 12: \[x, x, x, x, x, x, x\]
It is obvious that we can make two bouquets in different ways.
**Constraints:**
* `bloomDay.length == n`
* `1 <= n <= 105`
* `1 <= bloomDay[i] <= 109`
* `1 <= m <= 106`
* `1 <= k <= n` | Brute force for each array element. In order to improve the time complexity, we can sort the array and get the answer for each array element. |
Concise Python solution | how-many-numbers-are-smaller-than-the-current-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:\n a = []\n for i in nums:\n a.append(len([x for x in nums if x < i]))\n return a\n``` | 2 | Given the array `nums`, for each `nums[i]` find out how many numbers in the array are smaller than it. That is, for each `nums[i]` you have to count the number of valid `j's` such that `j != i` **and** `nums[j] < nums[i]`.
Return the answer in an array.
**Example 1:**
**Input:** nums = \[8,1,2,2,3\]
**Output:** \[4,0,1,1,3\]
**Explanation:**
For nums\[0\]=8 there exist four smaller numbers than it (1, 2, 2 and 3).
For nums\[1\]=1 does not exist any smaller number than it.
For nums\[2\]=2 there exist one smaller number than it (1).
For nums\[3\]=2 there exist one smaller number than it (1).
For nums\[4\]=3 there exist three smaller numbers than it (1, 2 and 2).
**Example 2:**
**Input:** nums = \[6,5,4,8\]
**Output:** \[2,1,0,3\]
**Example 3:**
**Input:** nums = \[7,7,7,7\]
**Output:** \[0,0,0,0\]
**Constraints:**
* `2 <= nums.length <= 500`
* `0 <= nums[i] <= 100` | null |
Concise Python solution | how-many-numbers-are-smaller-than-the-current-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:\n a = []\n for i in nums:\n a.append(len([x for x in nums if x < i]))\n return a\n``` | 2 | You are given an integer array `bloomDay`, an integer `m` and an integer `k`.
You want to make `m` bouquets. To make a bouquet, you need to use `k` **adjacent flowers** from the garden.
The garden consists of `n` flowers, the `ith` flower will bloom in the `bloomDay[i]` and then can be used in **exactly one** bouquet.
Return _the minimum number of days you need to wait to be able to make_ `m` _bouquets from the garden_. If it is impossible to make m bouquets return `-1`.
**Example 1:**
**Input:** bloomDay = \[1,10,3,10,2\], m = 3, k = 1
**Output:** 3
**Explanation:** Let us see what happened in the first three days. x means flower bloomed and \_ means flower did not bloom in the garden.
We need 3 bouquets each should contain 1 flower.
After day 1: \[x, \_, \_, \_, \_\] // we can only make one bouquet.
After day 2: \[x, \_, \_, \_, x\] // we can only make two bouquets.
After day 3: \[x, \_, x, \_, x\] // we can make 3 bouquets. The answer is 3.
**Example 2:**
**Input:** bloomDay = \[1,10,3,10,2\], m = 3, k = 2
**Output:** -1
**Explanation:** We need 3 bouquets each has 2 flowers, that means we need 6 flowers. We only have 5 flowers so it is impossible to get the needed bouquets and we return -1.
**Example 3:**
**Input:** bloomDay = \[7,7,7,7,12,7,7\], m = 2, k = 3
**Output:** 12
**Explanation:** We need 2 bouquets each should have 3 flowers.
Here is the garden after the 7 and 12 days:
After day 7: \[x, x, x, x, \_, x, x\]
We can make one bouquet of the first three flowers that bloomed. We cannot make another bouquet from the last three flowers that bloomed because they are not adjacent.
After day 12: \[x, x, x, x, x, x, x\]
It is obvious that we can make two bouquets in different ways.
**Constraints:**
* `bloomDay.length == n`
* `1 <= n <= 105`
* `1 <= bloomDay[i] <= 109`
* `1 <= m <= 106`
* `1 <= k <= n` | Brute force for each array element. In order to improve the time complexity, we can sort the array and get the answer for each array element. |
Brute Force Method & Sorting and Dictionary Method | how-many-numbers-are-smaller-than-the-current-number | 0 | 1 | # Brute Force Method: \n\n# Complexity\n- Time complexity:\nO(N^2) - It\'s kind of inefficient with larger inputs!\n\n# Code\n```\nclass Solution:\n def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:\n List = []\n for i in range(len(nums)):\n count = 0\n for j in range(len(nums)):\n if(j != i and nums[j] < nums[i]):\n count = count + 1\n List.append(count)\n return List\n\n\n```\n\n# Sorting and Dictionary Method: \n\n# Complexity\n- Time Complexity: \nO(NlogN)\n\n# Code\n```\nclass Solution:\n def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:\n sorted_nums = sorted(nums)\n count_dict = {}\n result = []\n for i, num in enumerate(sorted_nums):\n if num not in count_dict:\n count_dict[num] = i\n \n for num in nums:\n result.append(count_dict[num])\n \n return result\n\n``` | 4 | Given the array `nums`, for each `nums[i]` find out how many numbers in the array are smaller than it. That is, for each `nums[i]` you have to count the number of valid `j's` such that `j != i` **and** `nums[j] < nums[i]`.
Return the answer in an array.
**Example 1:**
**Input:** nums = \[8,1,2,2,3\]
**Output:** \[4,0,1,1,3\]
**Explanation:**
For nums\[0\]=8 there exist four smaller numbers than it (1, 2, 2 and 3).
For nums\[1\]=1 does not exist any smaller number than it.
For nums\[2\]=2 there exist one smaller number than it (1).
For nums\[3\]=2 there exist one smaller number than it (1).
For nums\[4\]=3 there exist three smaller numbers than it (1, 2 and 2).
**Example 2:**
**Input:** nums = \[6,5,4,8\]
**Output:** \[2,1,0,3\]
**Example 3:**
**Input:** nums = \[7,7,7,7\]
**Output:** \[0,0,0,0\]
**Constraints:**
* `2 <= nums.length <= 500`
* `0 <= nums[i] <= 100` | null |
Brute Force Method & Sorting and Dictionary Method | how-many-numbers-are-smaller-than-the-current-number | 0 | 1 | # Brute Force Method: \n\n# Complexity\n- Time complexity:\nO(N^2) - It\'s kind of inefficient with larger inputs!\n\n# Code\n```\nclass Solution:\n def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:\n List = []\n for i in range(len(nums)):\n count = 0\n for j in range(len(nums)):\n if(j != i and nums[j] < nums[i]):\n count = count + 1\n List.append(count)\n return List\n\n\n```\n\n# Sorting and Dictionary Method: \n\n# Complexity\n- Time Complexity: \nO(NlogN)\n\n# Code\n```\nclass Solution:\n def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:\n sorted_nums = sorted(nums)\n count_dict = {}\n result = []\n for i, num in enumerate(sorted_nums):\n if num not in count_dict:\n count_dict[num] = i\n \n for num in nums:\n result.append(count_dict[num])\n \n return result\n\n``` | 4 | You are given an integer array `bloomDay`, an integer `m` and an integer `k`.
You want to make `m` bouquets. To make a bouquet, you need to use `k` **adjacent flowers** from the garden.
The garden consists of `n` flowers, the `ith` flower will bloom in the `bloomDay[i]` and then can be used in **exactly one** bouquet.
Return _the minimum number of days you need to wait to be able to make_ `m` _bouquets from the garden_. If it is impossible to make m bouquets return `-1`.
**Example 1:**
**Input:** bloomDay = \[1,10,3,10,2\], m = 3, k = 1
**Output:** 3
**Explanation:** Let us see what happened in the first three days. x means flower bloomed and \_ means flower did not bloom in the garden.
We need 3 bouquets each should contain 1 flower.
After day 1: \[x, \_, \_, \_, \_\] // we can only make one bouquet.
After day 2: \[x, \_, \_, \_, x\] // we can only make two bouquets.
After day 3: \[x, \_, x, \_, x\] // we can make 3 bouquets. The answer is 3.
**Example 2:**
**Input:** bloomDay = \[1,10,3,10,2\], m = 3, k = 2
**Output:** -1
**Explanation:** We need 3 bouquets each has 2 flowers, that means we need 6 flowers. We only have 5 flowers so it is impossible to get the needed bouquets and we return -1.
**Example 3:**
**Input:** bloomDay = \[7,7,7,7,12,7,7\], m = 2, k = 3
**Output:** 12
**Explanation:** We need 2 bouquets each should have 3 flowers.
Here is the garden after the 7 and 12 days:
After day 7: \[x, x, x, x, \_, x, x\]
We can make one bouquet of the first three flowers that bloomed. We cannot make another bouquet from the last three flowers that bloomed because they are not adjacent.
After day 12: \[x, x, x, x, x, x, x\]
It is obvious that we can make two bouquets in different ways.
**Constraints:**
* `bloomDay.length == n`
* `1 <= n <= 105`
* `1 <= bloomDay[i] <= 109`
* `1 <= m <= 106`
* `1 <= k <= n` | Brute force for each array element. In order to improve the time complexity, we can sort the array and get the answer for each array element. |
Intuitive Python Solution (>95%) - Full Explanation + Good Variable Names | rank-teams-by-votes | 0 | 1 | # Intuition\n1. Use point vectors to keep track of positional rankings. (stored in a dictionary by team name as key)\n2. Use a decrementing point scale from N -> 0 to track rank of team at particular position (lower is better). N=number of votes.\n3. Sort return team list in ascending order based on primary criteria of points vector and secondary criteria of team name in alphabetical order \n** Because we are using a decreasing scale for the point vectors this allows for us to have to only sort in a single direction (ascending), meaning we only have to sort once.\n\nLet me know if you have any additional comments, questions, or improvements! \n\nPlease upvote if this helped you! :)\n\n# Approach\nExample 2: (from problem description)\n```\nInput: votes = ["WXYZ","XYZW"]\nOutput: "XWYZ"\n```\nWalkthrough\n```python\n## Visualizing votes\n# vote 1: [\'W\', \'X\', \'Y\', \'Z\']\n# vote 2: [\'X\', \'Y\', \'Z\', \'W\']\n\nnum_votes, num_teams = 2, 4\n\n# 1. Initial rank point vectors by team\nranks = {\n \'W\': [2, 2, 2, 2], \n \'X\': [2, 2, 2, 2], \n \'Y\': [2, 2, 2, 2], \n \'Z\': [2, 2, 2, 2]\n}\n# 2. Calculated rank point vectors by team\nranks = {\n \'W\': [1, 2, 2, 1],\n \'X\': [1, 1, 2, 2], \n \'Y\': [2, 1, 1, 2], \n \'Z\': [2, 2, 1, 1]\n}\n# 3. Sorted teams based on rank point vectors\nteams_sorted = [\n (\'X\', [1, 1, 2, 2]), \n (\'W\', [1, 2, 2, 1]), \n (\'Y\', [2, 1, 1, 2]), \n (\'Z\', [2, 2, 1, 1])\n]\n# 4. Formatted Output\nret = "XWYZ"\n```\n\n# Complexity\n- Time complexity:\n`O(T^2) + O(NT) + O(TLogT)`\n- Space complexity:\n`O(T^2) + O(NT) + O(T)`\n\n`* where N = number of votes, T = number of teams`\n\n```\n# Notable Constraints - N=num votes, T=num teams\n1 <= N <= 1000\n1 <= T <= 26 # A-Z -> 26 letters of the alphabet\n```\n# Code\n```\ndef rankTeams(self, votes: List[str]) -> str:\n # Initialize N, T\n num_votes, num_teams = len(votes), len(votes[0])\n \n # 1. Initialize ranks dict by team for point vector decrement\n # ranks = {"A": [N,N,...], "B": [N, N,...], ...} \n ranks = { team: [num_votes]*num_teams for team in votes[0] }\n\n # 2. Decrement team rank vector based on vote at each team index\n for i in range(num_teams):\n for vote in votes:\n team = vote[i]\n ranks[team][i] -= 1\n\n # 3. Sort teams based on the following in ASC order\n # a) vote point vectors\n # b) team name\n teams_sorted = sorted(ranks.items(), key=lambda x: (x[1], x[0]))\n \n # 4. Format return output\n ret = [team[0] for team in teams_sorted]\n return "".join(ret)\n``` | 14 | In a special ranking system, each voter gives a rank from highest to lowest to all teams participating in the competition.
The ordering of teams is decided by who received the most position-one votes. If two or more teams tie in the first position, we consider the second position to resolve the conflict, if they tie again, we continue this process until the ties are resolved. If two or more teams are still tied after considering all positions, we rank them alphabetically based on their team letter.
You are given an array of strings `votes` which is the votes of all voters in the ranking systems. Sort all teams according to the ranking system described above.
Return _a string of all teams **sorted** by the ranking system_.
**Example 1:**
**Input:** votes = \[ "ABC ", "ACB ", "ABC ", "ACB ", "ACB "\]
**Output:** "ACB "
**Explanation:**
Team A was ranked first place by 5 voters. No other team was voted as first place, so team A is the first team.
Team B was ranked second by 2 voters and ranked third by 3 voters.
Team C was ranked second by 3 voters and ranked third by 2 voters.
As most of the voters ranked C second, team C is the second team, and team B is the third.
**Example 2:**
**Input:** votes = \[ "WXYZ ", "XYZW "\]
**Output:** "XWYZ "
**Explanation:**
X is the winner due to the tie-breaking rule. X has the same votes as W for the first position, but X has one vote in the second position, while W does not have any votes in the second position.
**Example 3:**
**Input:** votes = \[ "ZMNAGUEDSJYLBOPHRQICWFXTVK "\]
**Output:** "ZMNAGUEDSJYLBOPHRQICWFXTVK "
**Explanation:** Only one voter, so their votes are used for the ranking.
**Constraints:**
* `1 <= votes.length <= 1000`
* `1 <= votes[i].length <= 26`
* `votes[i].length == votes[j].length` for `0 <= i, j < votes.length`.
* `votes[i][j]` is an English **uppercase** letter.
* All characters of `votes[i]` are unique.
* All the characters that occur in `votes[0]` **also occur** in `votes[j]` where `1 <= j < votes.length`. | Use doubly Linked list with hashmap of pointers to linked list nodes. add unique number to the linked list. When add is called check if the added number is unique then it have to be added to the linked list and if it is repeated remove it from the linked list if exists. When showFirstUnique is called retrieve the head of the linked list. Use queue and check that first element of the queue is always unique. Use set or heap to make running time of each function O(logn). |
Intuitive Python Solution (>95%) - Full Explanation + Good Variable Names | rank-teams-by-votes | 0 | 1 | # Intuition\n1. Use point vectors to keep track of positional rankings. (stored in a dictionary by team name as key)\n2. Use a decrementing point scale from N -> 0 to track rank of team at particular position (lower is better). N=number of votes.\n3. Sort return team list in ascending order based on primary criteria of points vector and secondary criteria of team name in alphabetical order \n** Because we are using a decreasing scale for the point vectors this allows for us to have to only sort in a single direction (ascending), meaning we only have to sort once.\n\nLet me know if you have any additional comments, questions, or improvements! \n\nPlease upvote if this helped you! :)\n\n# Approach\nExample 2: (from problem description)\n```\nInput: votes = ["WXYZ","XYZW"]\nOutput: "XWYZ"\n```\nWalkthrough\n```python\n## Visualizing votes\n# vote 1: [\'W\', \'X\', \'Y\', \'Z\']\n# vote 2: [\'X\', \'Y\', \'Z\', \'W\']\n\nnum_votes, num_teams = 2, 4\n\n# 1. Initial rank point vectors by team\nranks = {\n \'W\': [2, 2, 2, 2], \n \'X\': [2, 2, 2, 2], \n \'Y\': [2, 2, 2, 2], \n \'Z\': [2, 2, 2, 2]\n}\n# 2. Calculated rank point vectors by team\nranks = {\n \'W\': [1, 2, 2, 1],\n \'X\': [1, 1, 2, 2], \n \'Y\': [2, 1, 1, 2], \n \'Z\': [2, 2, 1, 1]\n}\n# 3. Sorted teams based on rank point vectors\nteams_sorted = [\n (\'X\', [1, 1, 2, 2]), \n (\'W\', [1, 2, 2, 1]), \n (\'Y\', [2, 1, 1, 2]), \n (\'Z\', [2, 2, 1, 1])\n]\n# 4. Formatted Output\nret = "XWYZ"\n```\n\n# Complexity\n- Time complexity:\n`O(T^2) + O(NT) + O(TLogT)`\n- Space complexity:\n`O(T^2) + O(NT) + O(T)`\n\n`* where N = number of votes, T = number of teams`\n\n```\n# Notable Constraints - N=num votes, T=num teams\n1 <= N <= 1000\n1 <= T <= 26 # A-Z -> 26 letters of the alphabet\n```\n# Code\n```\ndef rankTeams(self, votes: List[str]) -> str:\n # Initialize N, T\n num_votes, num_teams = len(votes), len(votes[0])\n \n # 1. Initialize ranks dict by team for point vector decrement\n # ranks = {"A": [N,N,...], "B": [N, N,...], ...} \n ranks = { team: [num_votes]*num_teams for team in votes[0] }\n\n # 2. Decrement team rank vector based on vote at each team index\n for i in range(num_teams):\n for vote in votes:\n team = vote[i]\n ranks[team][i] -= 1\n\n # 3. Sort teams based on the following in ASC order\n # a) vote point vectors\n # b) team name\n teams_sorted = sorted(ranks.items(), key=lambda x: (x[1], x[0]))\n \n # 4. Format return output\n ret = [team[0] for team in teams_sorted]\n return "".join(ret)\n``` | 14 | You are given a tree with `n` nodes numbered from `0` to `n - 1` in the form of a parent array `parent` where `parent[i]` is the parent of `ith` node. The root of the tree is node `0`. Find the `kth` ancestor of a given node.
The `kth` ancestor of a tree node is the `kth` node in the path from that node to the root node.
Implement the `TreeAncestor` class:
* `TreeAncestor(int n, int[] parent)` Initializes the object with the number of nodes in the tree and the parent array.
* `int getKthAncestor(int node, int k)` return the `kth` ancestor of the given node `node`. If there is no such ancestor, return `-1`.
**Example 1:**
**Input**
\[ "TreeAncestor ", "getKthAncestor ", "getKthAncestor ", "getKthAncestor "\]
\[\[7, \[-1, 0, 0, 1, 1, 2, 2\]\], \[3, 1\], \[5, 2\], \[6, 3\]\]
**Output**
\[null, 1, 0, -1\]
**Explanation**
TreeAncestor treeAncestor = new TreeAncestor(7, \[-1, 0, 0, 1, 1, 2, 2\]);
treeAncestor.getKthAncestor(3, 1); // returns 1 which is the parent of 3
treeAncestor.getKthAncestor(5, 2); // returns 0 which is the grandparent of 5
treeAncestor.getKthAncestor(6, 3); // returns -1 because there is no such ancestor
**Constraints:**
* `1 <= k <= n <= 5 * 104`
* `parent.length == n`
* `parent[0] == -1`
* `0 <= parent[i] < n` for all `0 < i < n`
* `0 <= node < n`
* There will be at most `5 * 104` queries. | Build array rank where rank[i][j] is the number of votes for team i to be the j-th rank. Sort the trams by rank array. if rank array is the same for two or more teams, sort them by the ID in ascending order. |
[python] O(N logN) solution, explained & easy-understanding | rank-teams-by-votes | 0 | 1 | ### Steps\n1. Create a ranking system for each char of each string in the array (hashmap), s.t.:\n\t```python\n\t\td = {\n\t\t\t\'A\': [0, 0, 0], # initialize array of size len(string)\n\t\t\t\'B\': [0, 0, 0],\n\t\t\t...\n\t\t}\n\t```\n2. For each char in the string, we add 1 to the position they are ranked,\n\te.g. `d[\'A\'] = [3, 0, 1]` means A is ranked first 3 times, second 0 times, and third once.\n\n3. Sort d.keys() based on their ranking values in dictionary, in descending order\n\tin case of equal votes, we alphabetically order the keys first using .sort()\n\n4. Join elements in the sorted list into a string\n\n### Complexity\n* time: O(N * S + N logN) ~ O(N logN)\n* space: O(N * S) ~ O(N)\n\nwhere N = # votes and S = length of a word in the `votes` array\n\t\tmax(S) is 26 chars so it would be constant O(1)\n\t\t\n### Python3\n```python\n def rankTeams(self, votes: List[str]) -> str:\n d = {}\n\n for vote in votes:\n for i, char in enumerate(vote):\n if char not in d:\n d[char] = [0] * len(vote)\n d[char][i] += 1\n\n voted_names = sorted(d.keys())\n return "".join(sorted(voted_names, key=lambda x: d[x], reverse=True))\n``` | 50 | In a special ranking system, each voter gives a rank from highest to lowest to all teams participating in the competition.
The ordering of teams is decided by who received the most position-one votes. If two or more teams tie in the first position, we consider the second position to resolve the conflict, if they tie again, we continue this process until the ties are resolved. If two or more teams are still tied after considering all positions, we rank them alphabetically based on their team letter.
You are given an array of strings `votes` which is the votes of all voters in the ranking systems. Sort all teams according to the ranking system described above.
Return _a string of all teams **sorted** by the ranking system_.
**Example 1:**
**Input:** votes = \[ "ABC ", "ACB ", "ABC ", "ACB ", "ACB "\]
**Output:** "ACB "
**Explanation:**
Team A was ranked first place by 5 voters. No other team was voted as first place, so team A is the first team.
Team B was ranked second by 2 voters and ranked third by 3 voters.
Team C was ranked second by 3 voters and ranked third by 2 voters.
As most of the voters ranked C second, team C is the second team, and team B is the third.
**Example 2:**
**Input:** votes = \[ "WXYZ ", "XYZW "\]
**Output:** "XWYZ "
**Explanation:**
X is the winner due to the tie-breaking rule. X has the same votes as W for the first position, but X has one vote in the second position, while W does not have any votes in the second position.
**Example 3:**
**Input:** votes = \[ "ZMNAGUEDSJYLBOPHRQICWFXTVK "\]
**Output:** "ZMNAGUEDSJYLBOPHRQICWFXTVK "
**Explanation:** Only one voter, so their votes are used for the ranking.
**Constraints:**
* `1 <= votes.length <= 1000`
* `1 <= votes[i].length <= 26`
* `votes[i].length == votes[j].length` for `0 <= i, j < votes.length`.
* `votes[i][j]` is an English **uppercase** letter.
* All characters of `votes[i]` are unique.
* All the characters that occur in `votes[0]` **also occur** in `votes[j]` where `1 <= j < votes.length`. | Use doubly Linked list with hashmap of pointers to linked list nodes. add unique number to the linked list. When add is called check if the added number is unique then it have to be added to the linked list and if it is repeated remove it from the linked list if exists. When showFirstUnique is called retrieve the head of the linked list. Use queue and check that first element of the queue is always unique. Use set or heap to make running time of each function O(logn). |
[python] O(N logN) solution, explained & easy-understanding | rank-teams-by-votes | 0 | 1 | ### Steps\n1. Create a ranking system for each char of each string in the array (hashmap), s.t.:\n\t```python\n\t\td = {\n\t\t\t\'A\': [0, 0, 0], # initialize array of size len(string)\n\t\t\t\'B\': [0, 0, 0],\n\t\t\t...\n\t\t}\n\t```\n2. For each char in the string, we add 1 to the position they are ranked,\n\te.g. `d[\'A\'] = [3, 0, 1]` means A is ranked first 3 times, second 0 times, and third once.\n\n3. Sort d.keys() based on their ranking values in dictionary, in descending order\n\tin case of equal votes, we alphabetically order the keys first using .sort()\n\n4. Join elements in the sorted list into a string\n\n### Complexity\n* time: O(N * S + N logN) ~ O(N logN)\n* space: O(N * S) ~ O(N)\n\nwhere N = # votes and S = length of a word in the `votes` array\n\t\tmax(S) is 26 chars so it would be constant O(1)\n\t\t\n### Python3\n```python\n def rankTeams(self, votes: List[str]) -> str:\n d = {}\n\n for vote in votes:\n for i, char in enumerate(vote):\n if char not in d:\n d[char] = [0] * len(vote)\n d[char][i] += 1\n\n voted_names = sorted(d.keys())\n return "".join(sorted(voted_names, key=lambda x: d[x], reverse=True))\n``` | 50 | You are given a tree with `n` nodes numbered from `0` to `n - 1` in the form of a parent array `parent` where `parent[i]` is the parent of `ith` node. The root of the tree is node `0`. Find the `kth` ancestor of a given node.
The `kth` ancestor of a tree node is the `kth` node in the path from that node to the root node.
Implement the `TreeAncestor` class:
* `TreeAncestor(int n, int[] parent)` Initializes the object with the number of nodes in the tree and the parent array.
* `int getKthAncestor(int node, int k)` return the `kth` ancestor of the given node `node`. If there is no such ancestor, return `-1`.
**Example 1:**
**Input**
\[ "TreeAncestor ", "getKthAncestor ", "getKthAncestor ", "getKthAncestor "\]
\[\[7, \[-1, 0, 0, 1, 1, 2, 2\]\], \[3, 1\], \[5, 2\], \[6, 3\]\]
**Output**
\[null, 1, 0, -1\]
**Explanation**
TreeAncestor treeAncestor = new TreeAncestor(7, \[-1, 0, 0, 1, 1, 2, 2\]);
treeAncestor.getKthAncestor(3, 1); // returns 1 which is the parent of 3
treeAncestor.getKthAncestor(5, 2); // returns 0 which is the grandparent of 5
treeAncestor.getKthAncestor(6, 3); // returns -1 because there is no such ancestor
**Constraints:**
* `1 <= k <= n <= 5 * 104`
* `parent.length == n`
* `parent[0] == -1`
* `0 <= parent[i] < n` for all `0 < i < n`
* `0 <= node < n`
* There will be at most `5 * 104` queries. | Build array rank where rank[i][j] is the number of votes for team i to be the j-th rank. Sort the trams by rank array. if rank array is the same for two or more teams, sort them by the ID in ascending order. |
python 3 || simple O(n)/O(1) solution | rank-teams-by-votes | 0 | 1 | ```\nclass Solution:\n def rankTeams(self, votes: List[str]) -> str:\n teamVotes = collections.defaultdict(lambda: [0] * 26)\n for vote in votes:\n for pos, team in enumerate(vote):\n teamVotes[team][pos] += 1\n \n return \'\'.join(sorted(teamVotes.keys(), reverse=True,\n key=lambda team: (teamVotes[team], -ord(team)))) | 5 | In a special ranking system, each voter gives a rank from highest to lowest to all teams participating in the competition.
The ordering of teams is decided by who received the most position-one votes. If two or more teams tie in the first position, we consider the second position to resolve the conflict, if they tie again, we continue this process until the ties are resolved. If two or more teams are still tied after considering all positions, we rank them alphabetically based on their team letter.
You are given an array of strings `votes` which is the votes of all voters in the ranking systems. Sort all teams according to the ranking system described above.
Return _a string of all teams **sorted** by the ranking system_.
**Example 1:**
**Input:** votes = \[ "ABC ", "ACB ", "ABC ", "ACB ", "ACB "\]
**Output:** "ACB "
**Explanation:**
Team A was ranked first place by 5 voters. No other team was voted as first place, so team A is the first team.
Team B was ranked second by 2 voters and ranked third by 3 voters.
Team C was ranked second by 3 voters and ranked third by 2 voters.
As most of the voters ranked C second, team C is the second team, and team B is the third.
**Example 2:**
**Input:** votes = \[ "WXYZ ", "XYZW "\]
**Output:** "XWYZ "
**Explanation:**
X is the winner due to the tie-breaking rule. X has the same votes as W for the first position, but X has one vote in the second position, while W does not have any votes in the second position.
**Example 3:**
**Input:** votes = \[ "ZMNAGUEDSJYLBOPHRQICWFXTVK "\]
**Output:** "ZMNAGUEDSJYLBOPHRQICWFXTVK "
**Explanation:** Only one voter, so their votes are used for the ranking.
**Constraints:**
* `1 <= votes.length <= 1000`
* `1 <= votes[i].length <= 26`
* `votes[i].length == votes[j].length` for `0 <= i, j < votes.length`.
* `votes[i][j]` is an English **uppercase** letter.
* All characters of `votes[i]` are unique.
* All the characters that occur in `votes[0]` **also occur** in `votes[j]` where `1 <= j < votes.length`. | Use doubly Linked list with hashmap of pointers to linked list nodes. add unique number to the linked list. When add is called check if the added number is unique then it have to be added to the linked list and if it is repeated remove it from the linked list if exists. When showFirstUnique is called retrieve the head of the linked list. Use queue and check that first element of the queue is always unique. Use set or heap to make running time of each function O(logn). |
python 3 || simple O(n)/O(1) solution | rank-teams-by-votes | 0 | 1 | ```\nclass Solution:\n def rankTeams(self, votes: List[str]) -> str:\n teamVotes = collections.defaultdict(lambda: [0] * 26)\n for vote in votes:\n for pos, team in enumerate(vote):\n teamVotes[team][pos] += 1\n \n return \'\'.join(sorted(teamVotes.keys(), reverse=True,\n key=lambda team: (teamVotes[team], -ord(team)))) | 5 | You are given a tree with `n` nodes numbered from `0` to `n - 1` in the form of a parent array `parent` where `parent[i]` is the parent of `ith` node. The root of the tree is node `0`. Find the `kth` ancestor of a given node.
The `kth` ancestor of a tree node is the `kth` node in the path from that node to the root node.
Implement the `TreeAncestor` class:
* `TreeAncestor(int n, int[] parent)` Initializes the object with the number of nodes in the tree and the parent array.
* `int getKthAncestor(int node, int k)` return the `kth` ancestor of the given node `node`. If there is no such ancestor, return `-1`.
**Example 1:**
**Input**
\[ "TreeAncestor ", "getKthAncestor ", "getKthAncestor ", "getKthAncestor "\]
\[\[7, \[-1, 0, 0, 1, 1, 2, 2\]\], \[3, 1\], \[5, 2\], \[6, 3\]\]
**Output**
\[null, 1, 0, -1\]
**Explanation**
TreeAncestor treeAncestor = new TreeAncestor(7, \[-1, 0, 0, 1, 1, 2, 2\]);
treeAncestor.getKthAncestor(3, 1); // returns 1 which is the parent of 3
treeAncestor.getKthAncestor(5, 2); // returns 0 which is the grandparent of 5
treeAncestor.getKthAncestor(6, 3); // returns -1 because there is no such ancestor
**Constraints:**
* `1 <= k <= n <= 5 * 104`
* `parent.length == n`
* `parent[0] == -1`
* `0 <= parent[i] < n` for all `0 < i < n`
* `0 <= node < n`
* There will be at most `5 * 104` queries. | Build array rank where rank[i][j] is the number of votes for team i to be the j-th rank. Sort the trams by rank array. if rank array is the same for two or more teams, sort them by the ID in ascending order. |
[Python3] Very Straightforward Solution | linked-list-in-binary-tree | 0 | 1 | # Code\n```\nclass Solution:\n def isSubPath(self, head: Optional[ListNode], root: Optional[TreeNode]) -> bool:\n \n self.graph = collections.defaultdict(list)\n self.lst = []\n tmp = head\n while tmp != None:\n self.lst.append(tmp)\n tmp = tmp.next\n\n def helper(root, parent):\n if not root: return\n if parent != None:\n self.graph[parent].append(root)\n self.graph[root].append(parent)\n\n helper(root.left, root)\n helper(root.right, root)\n \n helper(root, None)\n\n self.ans = False\n self.seen = set()\n\n\n def dfs(root, depth):\n if depth==len(self.lst):\n self.ans = True\n return\n for v in self.graph[root]:\n if v in self.seen: continue\n if v.val == self.lst[depth].val:\n self.seen.add(v)\n dfs(v, depth+1)\n self.seen.remove(v)\n \n def dfs2(root):\n if not root:\n return\n \n if root.val==head.val:\n self.seen.add(root)\n dfs(root, 1)\n self.seen.remove(root)\n \n dfs2(root.left)\n dfs2(root.right)\n\n dfs2(root)\n return self.ans\n``` | 1 | Given a binary tree `root` and a linked list with `head` as the first node.
Return True if all the elements in the linked list starting from the `head` correspond to some _downward path_ connected in the binary tree otherwise return False.
In this context downward path means a path that starts at some node and goes downwards.
**Example 1:**
**Input:** head = \[4,2,8\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** true
**Explanation:** Nodes in blue form a subpath in the binary Tree.
**Example 2:**
**Input:** head = \[1,4,2,6\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** true
**Example 3:**
**Input:** head = \[1,4,2,6,8\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** false
**Explanation:** There is no path in the binary tree that contains all the elements of the linked list from `head`.
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 2500]`.
* The number of nodes in the list will be in the range `[1, 100]`.
* `1 <= Node.val <= 100` for each node in the linked list and binary tree. | Does the dynamic programming sound like the right algorithm after sorting? Let's say box1 can be placed on top of box2. No matter what orientation box2 is in, we can rotate box1 so that it can be placed on top. Why don't we orient everything such that height is the biggest? |
✅ The Easiest Solution | linked-list-in-binary-tree | 0 | 1 | # Approach\nOrdinary DFS traversal is used. Each node of tree is checked to be part of the list - as easy as possible.\n\n# Complexity\n- Time complexity: $$O(n)$$ in most usual cases, $$O(n^2)$$ in the worst case, when the tree and list contain the same value but list is larger then tree height.\n\n- Space complexity: $$O(1)$$.\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isSubPath(self, head: Optional[ListNode], root: Optional[TreeNode]) -> bool:\n return self.traverseDFS(head, root)\n \n\n def traverseDFS(self, head, treeNode):\n if not treeNode:\n return False\n \n ret = self.checkDFS(head, treeNode)\n if ret:\n return ret\n\n ret = self.traverseDFS(head, treeNode.left)\n if ret:\n return ret\n \n return self.traverseDFS(head, treeNode.right)\n\n\n def checkDFS(self, listNode, treeNode):\n if listNode == None:\n return True\n elif treeNode == None:\n return False\n elif treeNode.val == listNode.val:\n ret = self.checkDFS(listNode.next, treeNode.left)\n if ret:\n return ret\n\n return self.checkDFS(listNode.next, treeNode.right)\n\n return False\n``` | 2 | Given a binary tree `root` and a linked list with `head` as the first node.
Return True if all the elements in the linked list starting from the `head` correspond to some _downward path_ connected in the binary tree otherwise return False.
In this context downward path means a path that starts at some node and goes downwards.
**Example 1:**
**Input:** head = \[4,2,8\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** true
**Explanation:** Nodes in blue form a subpath in the binary Tree.
**Example 2:**
**Input:** head = \[1,4,2,6\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** true
**Example 3:**
**Input:** head = \[1,4,2,6,8\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** false
**Explanation:** There is no path in the binary tree that contains all the elements of the linked list from `head`.
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 2500]`.
* The number of nodes in the list will be in the range `[1, 100]`.
* `1 <= Node.val <= 100` for each node in the linked list and binary tree. | Does the dynamic programming sound like the right algorithm after sorting? Let's say box1 can be placed on top of box2. No matter what orientation box2 is in, we can rotate box1 so that it can be placed on top. Why don't we orient everything such that height is the biggest? |
Python : Fastest Approach | linked-list-in-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isSubPath(self, head: Optional[ListNode], root: Optional[TreeNode]) -> bool:\n\n if head is None:\n return True\n\n if root is None:\n return False\n\n if head.val == root.val:\n if self.isSame(head, root):\n return True\n \n return self.isSubPath(head, root.left) or self.isSubPath(head, root.right)\n\n \n def isSame(self, head, root):\n\n if head is None:\n return True\n \n if root is None:\n return False\n\n if head.val == root.val:\n return self.isSame(head.next, root.left) or self.isSame(head.next, root.right)\n \n return False\n \n\n``` | 1 | Given a binary tree `root` and a linked list with `head` as the first node.
Return True if all the elements in the linked list starting from the `head` correspond to some _downward path_ connected in the binary tree otherwise return False.
In this context downward path means a path that starts at some node and goes downwards.
**Example 1:**
**Input:** head = \[4,2,8\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** true
**Explanation:** Nodes in blue form a subpath in the binary Tree.
**Example 2:**
**Input:** head = \[1,4,2,6\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** true
**Example 3:**
**Input:** head = \[1,4,2,6,8\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** false
**Explanation:** There is no path in the binary tree that contains all the elements of the linked list from `head`.
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 2500]`.
* The number of nodes in the list will be in the range `[1, 100]`.
* `1 <= Node.val <= 100` for each node in the linked list and binary tree. | Does the dynamic programming sound like the right algorithm after sorting? Let's say box1 can be placed on top of box2. No matter what orientation box2 is in, we can rotate box1 so that it can be placed on top. Why don't we orient everything such that height is the biggest? |
🔥[Python 3] BFS + DFS combination | linked-list-in-binary-tree | 0 | 1 | ### Time complexity: \n`O(N) * min(O(H), O(L))`\nwhere N - tree size, H - tree height, L - list length\n```python3 []\nclass Solution:\n def isSubPath(self, head: Optional[ListNode], root: Optional[TreeNode]) -> bool:\n def isEqual(treeNode, listNode):\n if not listNode: return True\n if not treeNode or treeNode.val != listNode.val: return False\n return isEqual(treeNode.left, listNode.next) or isEqual(treeNode.right, listNode.next)\n\n queue = deque([root])\n while queue:\n for _ in range(len(queue)):\n cur = queue.popleft()\n if cur.val == head.val and isEqual(cur, head):\n return True\n if cur.left: queue.append(cur.left)\n if cur.right: queue.append(cur.right)\n \n return False\n``` | 3 | Given a binary tree `root` and a linked list with `head` as the first node.
Return True if all the elements in the linked list starting from the `head` correspond to some _downward path_ connected in the binary tree otherwise return False.
In this context downward path means a path that starts at some node and goes downwards.
**Example 1:**
**Input:** head = \[4,2,8\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** true
**Explanation:** Nodes in blue form a subpath in the binary Tree.
**Example 2:**
**Input:** head = \[1,4,2,6\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** true
**Example 3:**
**Input:** head = \[1,4,2,6,8\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** false
**Explanation:** There is no path in the binary tree that contains all the elements of the linked list from `head`.
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 2500]`.
* The number of nodes in the list will be in the range `[1, 100]`.
* `1 <= Node.val <= 100` for each node in the linked list and binary tree. | Does the dynamic programming sound like the right algorithm after sorting? Let's say box1 can be placed on top of box2. No matter what orientation box2 is in, we can rotate box1 so that it can be placed on top. Why don't we orient everything such that height is the biggest? |
[Python3] 0-1 BFS - Simple Solution | minimum-cost-to-make-at-least-one-valid-path-in-a-grid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(M * N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(M * N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCost(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n distance = [[m * n + 1 for _ in range(n)] for _ in range(m)]\n distance[0][0] = 0\n q = collections.deque([(0, 0, 0)])\n while q:\n c, i, j = q.popleft()\n if c > distance[i][j]: continue\n if i == m - 1 and j == n - 1: return c\n for di, dj, d in [(0, 1, 1), (0, -1, 2), (1, 0, 3), (-1, 0, 4)]:\n ci, cj = i + di, j + dj\n if 0 <= ci < m and 0 <= cj < n:\n if c + int(d != grid[i][j]) < distance[ci][cj]:\n distance[ci][cj] = c + int(d != grid[i][j])\n if d == grid[i][j]: q.appendleft((distance[ci][cj], ci, cj))\n else: q.append((distance[ci][cj], ci, cj))\n \n return distance[m - 1][n - 1]\n``` | 1 | Given an `m x n` grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of `grid[i][j]` can be:
* `1` which means go to the cell to the right. (i.e go from `grid[i][j]` to `grid[i][j + 1]`)
* `2` which means go to the cell to the left. (i.e go from `grid[i][j]` to `grid[i][j - 1]`)
* `3` which means go to the lower cell. (i.e go from `grid[i][j]` to `grid[i + 1][j]`)
* `4` which means go to the upper cell. (i.e go from `grid[i][j]` to `grid[i - 1][j]`)
Notice that there could be some signs on the cells of the grid that point outside the grid.
You will initially start at the upper left cell `(0, 0)`. A valid path in the grid is a path that starts from the upper left cell `(0, 0)` and ends at the bottom-right cell `(m - 1, n - 1)` following the signs on the grid. The valid path does not have to be the shortest.
You can modify the sign on a cell with `cost = 1`. You can modify the sign on a cell **one time only**.
Return _the minimum cost to make the grid have at least one valid path_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1\],\[2,2,2,2\],\[1,1,1,1\],\[2,2,2,2\]\]
**Output:** 3
**Explanation:** You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.
**Example 2:**
**Input:** grid = \[\[1,1,3\],\[3,2,2\],\[1,1,4\]\]
**Output:** 0
**Explanation:** You can follow the path from (0, 0) to (2, 2).
**Example 3:**
**Input:** grid = \[\[1,2\],\[4,3\]\]
**Output:** 1
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `1 <= grid[i][j] <= 4` | null |
python bfs with heap | minimum-cost-to-make-at-least-one-valid-path-in-a-grid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCost(self, grid: List[List[int]]) -> int:\n def gen_next(p):\n directions = [(0,-1,2), (0,1,1), (1,0,3), (-1,0,4)]\n for x, y, d in directions:\n yield x, y, (0 if d == p else 1)\n visited = set()\n q = [(0,0,0)]\n while len(q) > 0:\n cost, x, y = heapq.heappop(q)\n if x == len(grid) - 1 and y == len(grid[0]) - 1:\n return cost\n if (x, y) not in visited:\n visited.add((x,y))\n for dx, dy, c in gen_next(grid[x][y]):\n new_x, new_y = x + dx, y + dy\n if 0 <= new_y < len(grid[0]) and 0 <= new_x < len(grid):\n heapq.heappush(q, (cost+c, new_x, new_y))\n\n\n``` | 1 | Given an `m x n` grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of `grid[i][j]` can be:
* `1` which means go to the cell to the right. (i.e go from `grid[i][j]` to `grid[i][j + 1]`)
* `2` which means go to the cell to the left. (i.e go from `grid[i][j]` to `grid[i][j - 1]`)
* `3` which means go to the lower cell. (i.e go from `grid[i][j]` to `grid[i + 1][j]`)
* `4` which means go to the upper cell. (i.e go from `grid[i][j]` to `grid[i - 1][j]`)
Notice that there could be some signs on the cells of the grid that point outside the grid.
You will initially start at the upper left cell `(0, 0)`. A valid path in the grid is a path that starts from the upper left cell `(0, 0)` and ends at the bottom-right cell `(m - 1, n - 1)` following the signs on the grid. The valid path does not have to be the shortest.
You can modify the sign on a cell with `cost = 1`. You can modify the sign on a cell **one time only**.
Return _the minimum cost to make the grid have at least one valid path_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1\],\[2,2,2,2\],\[1,1,1,1\],\[2,2,2,2\]\]
**Output:** 3
**Explanation:** You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.
**Example 2:**
**Input:** grid = \[\[1,1,3\],\[3,2,2\],\[1,1,4\]\]
**Output:** 0
**Explanation:** You can follow the path from (0, 0) to (2, 2).
**Example 3:**
**Input:** grid = \[\[1,2\],\[4,3\]\]
**Output:** 1
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `1 <= grid[i][j] <= 4` | null |
[Python] O(MN), simple BFS with explanation | minimum-cost-to-make-at-least-one-valid-path-in-a-grid | 0 | 1 | **Idea**\nThis is a typical BFS question on Graph. \nEssentially, we need to track `visited` nodes to eliminate duplicated exploration, which both affect correctness and efficiency.\n\n**Complexity**\nTime: `O(mn)`\nSpace: `O(mn)`\n\n**Python 3, BFS**\n```\nclass Solution:\n def minCost(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n arrow = [(0,1), (0,-1), (1,0), (-1,0)] \n dp, costs = collections.deque([(0,0,0)]), {}\n \n while dp:\n nx, ny, cost = dp.popleft()\n while 0 <= nx < m and 0 <= ny < n and (nx, ny) not in costs:\n costs[nx, ny] = cost\n dp += [(nx+dx, ny+dy, cost+1) for dx, dy in arrow]\n dx, dy = arrow[grid[nx][ny]-1]\n nx, ny = nx+dx, ny+dy\n \n return costs[m-1,n-1] \n``` | 30 | Given an `m x n` grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of `grid[i][j]` can be:
* `1` which means go to the cell to the right. (i.e go from `grid[i][j]` to `grid[i][j + 1]`)
* `2` which means go to the cell to the left. (i.e go from `grid[i][j]` to `grid[i][j - 1]`)
* `3` which means go to the lower cell. (i.e go from `grid[i][j]` to `grid[i + 1][j]`)
* `4` which means go to the upper cell. (i.e go from `grid[i][j]` to `grid[i - 1][j]`)
Notice that there could be some signs on the cells of the grid that point outside the grid.
You will initially start at the upper left cell `(0, 0)`. A valid path in the grid is a path that starts from the upper left cell `(0, 0)` and ends at the bottom-right cell `(m - 1, n - 1)` following the signs on the grid. The valid path does not have to be the shortest.
You can modify the sign on a cell with `cost = 1`. You can modify the sign on a cell **one time only**.
Return _the minimum cost to make the grid have at least one valid path_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1\],\[2,2,2,2\],\[1,1,1,1\],\[2,2,2,2\]\]
**Output:** 3
**Explanation:** You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.
**Example 2:**
**Input:** grid = \[\[1,1,3\],\[3,2,2\],\[1,1,4\]\]
**Output:** 0
**Explanation:** You can follow the path from (0, 0) to (2, 2).
**Example 3:**
**Input:** grid = \[\[1,2\],\[4,3\]\]
**Output:** 1
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `1 <= grid[i][j] <= 4` | null |
Python 3 || dfs & bfs, no recursion || T/M: 94% / 98% | minimum-cost-to-make-at-least-one-valid-path-in-a-grid | 0 | 1 | We re-use grid to keep track of `seen`.\n```\nclass Solution:\n def minCost(self, grid: List[List[int]]) -> int:\n\n m, n, cost, queue = len(grid), len(grid[0]), 0, deque()\n M, N = range(m), range(n)\n\n seen = lambda x,y : not x in M or y not in N or not grid[x][y]\n dir = ((),(0,1), (0,-1), (1,0), (-1,0))\n\n def dfs(x: int,y: int)->None:\n while not seen(x,y):\n (dx,dy), grid[x][y] = dir[grid[x][y]], None\n queue.append((x,y))\n x,y = x+dx, y+dy\n return\n\n dfs(0, 0)\n\n while queue:\n if (m-1, n-1) in queue: return cost\n cost += 1\n q = len(queue)\n\n for _ in range(q):\n x, y = queue.popleft()\n for dx,dy in dir[1:]:\n dfs(x+dx, y+dy)\n```\n[https://leetcode.com/problems/minimum-cost-to-make-at-least-one-valid-path-in-a-grid/submissions/878791604/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*MN*) and space complexity is worstcase\n *O*(*MN*). | 5 | Given an `m x n` grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of `grid[i][j]` can be:
* `1` which means go to the cell to the right. (i.e go from `grid[i][j]` to `grid[i][j + 1]`)
* `2` which means go to the cell to the left. (i.e go from `grid[i][j]` to `grid[i][j - 1]`)
* `3` which means go to the lower cell. (i.e go from `grid[i][j]` to `grid[i + 1][j]`)
* `4` which means go to the upper cell. (i.e go from `grid[i][j]` to `grid[i - 1][j]`)
Notice that there could be some signs on the cells of the grid that point outside the grid.
You will initially start at the upper left cell `(0, 0)`. A valid path in the grid is a path that starts from the upper left cell `(0, 0)` and ends at the bottom-right cell `(m - 1, n - 1)` following the signs on the grid. The valid path does not have to be the shortest.
You can modify the sign on a cell with `cost = 1`. You can modify the sign on a cell **one time only**.
Return _the minimum cost to make the grid have at least one valid path_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1\],\[2,2,2,2\],\[1,1,1,1\],\[2,2,2,2\]\]
**Output:** 3
**Explanation:** You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.
**Example 2:**
**Input:** grid = \[\[1,1,3\],\[3,2,2\],\[1,1,4\]\]
**Output:** 0
**Explanation:** You can follow the path from (0, 0) to (2, 2).
**Example 3:**
**Input:** grid = \[\[1,2\],\[4,3\]\]
**Output:** 1
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `1 <= grid[i][j] <= 4` | null |
63% TC and 78% SC easy python solution | minimum-cost-to-make-at-least-one-valid-path-in-a-grid | 0 | 1 | ```\ndef minCost(self, grid: List[List[int]]) -> int:\n\tm, n = len(grid), len(grid[0])\n\tdir = [(0, 1), (0, -1), (1, 0), (-1, 0)] \n\t# in order of grid value for direction\n\tdis = [[float(\'inf\')] * n for _ in range(m)]\n\tdis[0][0] = 0\n\theap = [(dis[0][0], [0, 0])]\n\twhile(heap):\n\t\td, [i, j] = heappop(heap)\n\t\tfor x, y in dir:\n\t\t\tif(0<=i+x<m and 0<=j+y<n):\n\t\t\t\tif((x, y) == dir[grid[i][j]-1] and dis[i+x][j+y] > d):\n\t\t\t\t\tdis[i+x][j+y] = d\n\t\t\t\t\theappush(heap, (d, [i+x, j+y]))\n\t\t\t\telif(dis[i+x][j+y] > 1+d):\n\t\t\t\t\tdis[i+x][j+y] = 1+d\n\t\t\t\t\theappush(heap, (d+1, [i+x, j+y]))\n\treturn dis[-1][-1]\n``` | 1 | Given an `m x n` grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of `grid[i][j]` can be:
* `1` which means go to the cell to the right. (i.e go from `grid[i][j]` to `grid[i][j + 1]`)
* `2` which means go to the cell to the left. (i.e go from `grid[i][j]` to `grid[i][j - 1]`)
* `3` which means go to the lower cell. (i.e go from `grid[i][j]` to `grid[i + 1][j]`)
* `4` which means go to the upper cell. (i.e go from `grid[i][j]` to `grid[i - 1][j]`)
Notice that there could be some signs on the cells of the grid that point outside the grid.
You will initially start at the upper left cell `(0, 0)`. A valid path in the grid is a path that starts from the upper left cell `(0, 0)` and ends at the bottom-right cell `(m - 1, n - 1)` following the signs on the grid. The valid path does not have to be the shortest.
You can modify the sign on a cell with `cost = 1`. You can modify the sign on a cell **one time only**.
Return _the minimum cost to make the grid have at least one valid path_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1\],\[2,2,2,2\],\[1,1,1,1\],\[2,2,2,2\]\]
**Output:** 3
**Explanation:** You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.
**Example 2:**
**Input:** grid = \[\[1,1,3\],\[3,2,2\],\[1,1,4\]\]
**Output:** 0
**Explanation:** You can follow the path from (0, 0) to (2, 2).
**Example 3:**
**Input:** grid = \[\[1,2\],\[4,3\]\]
**Output:** 1
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `1 <= grid[i][j] <= 4` | null |
Python | Template | 0-1 BFS vs Dijkstra | Explanation | minimum-cost-to-make-at-least-one-valid-path-in-a-grid | 0 | 1 | * I modelled the graph such that each cell in grid has 4 neighbors and cost to a neighbor is 0 if grid has value pointing to that direction, else cost = 1\n* 0-1 BFS appends to the left if neighbor cost is same as current node cost. Else, it appends to the end. The idea comes from standard BFS and Dijsktra to use a queue and give some priority to nodes with shorter distance without compromising on time (O(1) to insert into Queue rather than O(logV))\n* Both algorithms took approx same time because the input size is less ~ 600 ms\n```\nclass Solution:\n def minCost(self, grid: List[List[int]]) -> int:\n graph = {}\n m, n = len(grid), len(grid[0])\n \n def addEdges(i, j):\n graph[(i, j)] = {}\n neighbors = [(i + 1, j), (i - 1, j), (i, j + 1), (i, j - 1)]\n for each in neighbors:\n x, y = each\n if x < 0 or y < 0 or x > m - 1 or y > n - 1:\n continue\n else:\n graph[(i, j)][(x, y)] = 1\n \n if grid[i][j] == 1:\n if j != n - 1:\n graph[(i, j)][(i, j + 1)] = 0\n \n elif grid[i][j] == 2:\n if j != 0:\n graph[(i, j)][(i, j - 1)] = 0\n \n elif grid[i][j] == 3:\n if i != m - 1:\n graph[(i, j)][(i + 1, j)] = 0\n \n else:\n if i != 0:\n graph[(i, j)][(i - 1, j)] = 0\n \n \n for i in range(m):\n for j in range(n):\n addEdges(i, j)\n \n\t\t# convert row, col to index value in distances array\n def convert(x, y):\n return x * n + y\n \n def BFS(graph):\n q = deque()\n q.append([0, 0, 0])\n distances = [float(inf)] * (m * n)\n \n while q:\n cost, x, y = q.popleft()\n if (x, y) == (m - 1, n - 1):\n return cost\n \n idx = convert(x, y)\n if distances[idx] < cost:\n continue\n \n distances[idx] = cost\n for node, nxtCost in graph[(x, y)].items():\n nxtIndex = convert(node[0], node[1])\n if distances[nxtIndex] <= cost + nxtCost:\n continue\n \n distances[nxtIndex] = cost + nxtCost\n if nxtCost == 0:\n q.appendleft([cost, node[0], node[1]])\n else:\n q.append([cost + 1, node[0], node[1]])\n \n \n def dijkstra(graph):\n distances = [float(inf)] * (m * n)\n myheap = [[0, 0, 0]]\n #distances[0] = 0\n \n while myheap:\n cost, x, y = heappop(myheap)\n if (x, y) == (m - 1, n - 1):\n return cost\n \n idx = convert(x, y)\n if distances[idx] < cost:\n continue\n else:\n distances[idx] = cost\n for node, nxtCost in graph[(x, y)].items():\n total = cost + nxtCost\n nxtIndex = convert(node[0], node[1])\n if distances[nxtIndex] <= total:\n continue\n else:\n distances[nxtIndex] = total\n heappush(myheap, [total, node[0], node[1]])\n \n return distances[-1]\n \n #return dijkstra(graph)\n return BFS(graph) | 3 | Given an `m x n` grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of `grid[i][j]` can be:
* `1` which means go to the cell to the right. (i.e go from `grid[i][j]` to `grid[i][j + 1]`)
* `2` which means go to the cell to the left. (i.e go from `grid[i][j]` to `grid[i][j - 1]`)
* `3` which means go to the lower cell. (i.e go from `grid[i][j]` to `grid[i + 1][j]`)
* `4` which means go to the upper cell. (i.e go from `grid[i][j]` to `grid[i - 1][j]`)
Notice that there could be some signs on the cells of the grid that point outside the grid.
You will initially start at the upper left cell `(0, 0)`. A valid path in the grid is a path that starts from the upper left cell `(0, 0)` and ends at the bottom-right cell `(m - 1, n - 1)` following the signs on the grid. The valid path does not have to be the shortest.
You can modify the sign on a cell with `cost = 1`. You can modify the sign on a cell **one time only**.
Return _the minimum cost to make the grid have at least one valid path_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1\],\[2,2,2,2\],\[1,1,1,1\],\[2,2,2,2\]\]
**Output:** 3
**Explanation:** You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.
**Example 2:**
**Input:** grid = \[\[1,1,3\],\[3,2,2\],\[1,1,4\]\]
**Output:** 0
**Explanation:** You can follow the path from (0, 0) to (2, 2).
**Example 3:**
**Input:** grid = \[\[1,2\],\[4,3\]\]
**Output:** 1
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `1 <= grid[i][j] <= 4` | null |
Simple Java Solution - Count Array | increasing-decreasing-string | 1 | 1 | # Code\n```\nclass Solution {\n public String sortString(String s) {\n int[] alpha = new int[27];\n for(char ch : s.toCharArray())\n {\n alpha[ch-\'a\']++;\n }\n String result = "";\n boolean flag = false;\n while(flag!=true)\n {\n flag = true;\n for(int i = 0;i<27;i++)\n {\n if(alpha[i]!=0)\n {\n result = result+(char)(i+97);\n alpha[i]--;\n flag = false;\n }\n }\n flag = true;\n for(int j = 26;j>=0;j--)\n {\n if(alpha[j]!=0)\n {\n result = result+(char)(j+97);\n alpha[j]--;\n flag = false;\n }\n }\n }\n return result;\n }\n}\n``` | 2 | You are given a string `s`. Reorder the string using the following algorithm:
1. Pick the **smallest** character from `s` and **append** it to the result.
2. Pick the **smallest** character from `s` which is greater than the last appended character to the result and **append** it.
3. Repeat step 2 until you cannot pick more characters.
4. Pick the **largest** character from `s` and **append** it to the result.
5. Pick the **largest** character from `s` which is smaller than the last appended character to the result and **append** it.
6. Repeat step 5 until you cannot pick more characters.
7. Repeat the steps from 1 to 6 until you pick all characters from `s`.
In each step, If the smallest or the largest character appears more than once you can choose any occurrence and append it to the result.
Return _the result string after sorting_ `s` _with this algorithm_.
**Example 1:**
**Input:** s = "aaaabbbbcccc "
**Output:** "abccbaabccba "
**Explanation:** After steps 1, 2 and 3 of the first iteration, result = "abc "
After steps 4, 5 and 6 of the first iteration, result = "abccba "
First iteration is done. Now s = "aabbcc " and we go back to step 1
After steps 1, 2 and 3 of the second iteration, result = "abccbaabc "
After steps 4, 5 and 6 of the second iteration, result = "abccbaabccba "
**Example 2:**
**Input:** s = "rat "
**Output:** "art "
**Explanation:** The word "rat " becomes "art " after re-ordering it with the mentioned algorithm.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | After replacing each even by zero and every odd by one can we use prefix sum to find answer ? Can we use two pointers to count number of sub-arrays ? Can we store indices of odd numbers and for each k indices count number of sub-arrays contains them ? |
Simple solution by Python 3 | increasing-decreasing-string | 0 | 1 | ```\nclass Solution:\n def sortString(self, s: str) -> str:\n s = list(s)\n result = \'\'\n while s:\n for letter in sorted(set(s)):\n s.remove(letter)\n result += letter\n for letter in sorted(set(s), reverse=True):\n s.remove(letter)\n result += letter\n return result\n``` | 64 | You are given a string `s`. Reorder the string using the following algorithm:
1. Pick the **smallest** character from `s` and **append** it to the result.
2. Pick the **smallest** character from `s` which is greater than the last appended character to the result and **append** it.
3. Repeat step 2 until you cannot pick more characters.
4. Pick the **largest** character from `s` and **append** it to the result.
5. Pick the **largest** character from `s` which is smaller than the last appended character to the result and **append** it.
6. Repeat step 5 until you cannot pick more characters.
7. Repeat the steps from 1 to 6 until you pick all characters from `s`.
In each step, If the smallest or the largest character appears more than once you can choose any occurrence and append it to the result.
Return _the result string after sorting_ `s` _with this algorithm_.
**Example 1:**
**Input:** s = "aaaabbbbcccc "
**Output:** "abccbaabccba "
**Explanation:** After steps 1, 2 and 3 of the first iteration, result = "abc "
After steps 4, 5 and 6 of the first iteration, result = "abccba "
First iteration is done. Now s = "aabbcc " and we go back to step 1
After steps 1, 2 and 3 of the second iteration, result = "abccbaabc "
After steps 4, 5 and 6 of the second iteration, result = "abccbaabccba "
**Example 2:**
**Input:** s = "rat "
**Output:** "art "
**Explanation:** The word "rat " becomes "art " after re-ordering it with the mentioned algorithm.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | After replacing each even by zero and every odd by one can we use prefix sum to find answer ? Can we use two pointers to count number of sub-arrays ? Can we store indices of odd numbers and for each k indices count number of sub-arrays contains them ? |
Python | Using dict | Beats 95% | increasing-decreasing-string | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCreate a frequency map of s.\n\nIterate over all the letters of s in sorted manner and add that character to result .\n\nRepeat above step but for reversed string.\n \nIf the frequency becomes 0 then we delete the key from dict.\n\n# Code\n```\nclass Solution:\n def sortString(self, s: str) -> str:\n freq = {}\n letters = sorted(set(s))\n res = ""\n for i in s:\n if i in freq:\n freq[i]+=1\n else:\n freq[i] = 1\n while freq:\n for i in letters:\n if i in freq:\n if freq[i]>0:\n res+=i\n freq[i]-=1\n else:\n del freq[i]\n\n for i in letters[::-1]:\n if i in freq:\n if freq[i]>0:\n res+=i\n freq[i]-=1\n else:\n del freq[i]\n\n\n return res\n\n``` | 2 | You are given a string `s`. Reorder the string using the following algorithm:
1. Pick the **smallest** character from `s` and **append** it to the result.
2. Pick the **smallest** character from `s` which is greater than the last appended character to the result and **append** it.
3. Repeat step 2 until you cannot pick more characters.
4. Pick the **largest** character from `s` and **append** it to the result.
5. Pick the **largest** character from `s` which is smaller than the last appended character to the result and **append** it.
6. Repeat step 5 until you cannot pick more characters.
7. Repeat the steps from 1 to 6 until you pick all characters from `s`.
In each step, If the smallest or the largest character appears more than once you can choose any occurrence and append it to the result.
Return _the result string after sorting_ `s` _with this algorithm_.
**Example 1:**
**Input:** s = "aaaabbbbcccc "
**Output:** "abccbaabccba "
**Explanation:** After steps 1, 2 and 3 of the first iteration, result = "abc "
After steps 4, 5 and 6 of the first iteration, result = "abccba "
First iteration is done. Now s = "aabbcc " and we go back to step 1
After steps 1, 2 and 3 of the second iteration, result = "abccbaabc "
After steps 4, 5 and 6 of the second iteration, result = "abccbaabccba "
**Example 2:**
**Input:** s = "rat "
**Output:** "art "
**Explanation:** The word "rat " becomes "art " after re-ordering it with the mentioned algorithm.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | After replacing each even by zero and every odd by one can we use prefix sum to find answer ? Can we use two pointers to count number of sub-arrays ? Can we store indices of odd numbers and for each k indices count number of sub-arrays contains them ? |
[Python] Easy-to-understand solution explained | increasing-decreasing-string | 0 | 1 | Steps:\n1. Count the number of occurrences of every letter.\n2. Sort in alphabetic order.\n3. Follow the procedure defined in the problem statement.\n```python\ndef sortString(self, s: str) -> str:\n d = sorted([c, n] for c, n in collections.Counter(s).items())\n r = []\n while len(r) < len(s):\n for i in range(len(d)):\n if d[i][1]:\n r.append(d[i][0])\n d[i][1] -= 1\n for i in range(len(d)):\n if d[~i][1]:\n r.append(d[~i][0])\n d[~i][1] -= 1\n return \'\'.join(r)\n```\nVote up if you find this helpful, thanks! | 51 | You are given a string `s`. Reorder the string using the following algorithm:
1. Pick the **smallest** character from `s` and **append** it to the result.
2. Pick the **smallest** character from `s` which is greater than the last appended character to the result and **append** it.
3. Repeat step 2 until you cannot pick more characters.
4. Pick the **largest** character from `s` and **append** it to the result.
5. Pick the **largest** character from `s` which is smaller than the last appended character to the result and **append** it.
6. Repeat step 5 until you cannot pick more characters.
7. Repeat the steps from 1 to 6 until you pick all characters from `s`.
In each step, If the smallest or the largest character appears more than once you can choose any occurrence and append it to the result.
Return _the result string after sorting_ `s` _with this algorithm_.
**Example 1:**
**Input:** s = "aaaabbbbcccc "
**Output:** "abccbaabccba "
**Explanation:** After steps 1, 2 and 3 of the first iteration, result = "abc "
After steps 4, 5 and 6 of the first iteration, result = "abccba "
First iteration is done. Now s = "aabbcc " and we go back to step 1
After steps 1, 2 and 3 of the second iteration, result = "abccbaabc "
After steps 4, 5 and 6 of the second iteration, result = "abccbaabccba "
**Example 2:**
**Input:** s = "rat "
**Output:** "art "
**Explanation:** The word "rat " becomes "art " after re-ordering it with the mentioned algorithm.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | After replacing each even by zero and every odd by one can we use prefix sum to find answer ? Can we use two pointers to count number of sub-arrays ? Can we store indices of odd numbers and for each k indices count number of sub-arrays contains them ? |
[Python 3] Using Set and Sort with commentary | increasing-decreasing-string | 0 | 1 | ```\nclass Solution:\n def sortString(self, s: str) -> str:\n s = list(s)\n # Big S: O(n)\n result = []\n \n # Logic is capture distinct char with set\n # Remove found char from initial string\n \n # Big O: O(n)\n while len(s) > 0:\n\n # Big O: O(n log n) Space: O(n)\n smallest = sorted(set(s))\n # Big O: O(s) - reduced set\n for small in smallest:\n result.append(small)\n s.remove(small)\n \n # Big O: O(n log n) Space: O(n)\n largest = sorted(set(s), reverse = True)\n # Big O: O(s) - reduced set\n for large in largest:\n result.append(large)\n s.remove(large)\n \n return \'\'.join(result)\n \n # Summary: Big O(n)^2 Space: O(n)\n``` | 12 | You are given a string `s`. Reorder the string using the following algorithm:
1. Pick the **smallest** character from `s` and **append** it to the result.
2. Pick the **smallest** character from `s` which is greater than the last appended character to the result and **append** it.
3. Repeat step 2 until you cannot pick more characters.
4. Pick the **largest** character from `s` and **append** it to the result.
5. Pick the **largest** character from `s` which is smaller than the last appended character to the result and **append** it.
6. Repeat step 5 until you cannot pick more characters.
7. Repeat the steps from 1 to 6 until you pick all characters from `s`.
In each step, If the smallest or the largest character appears more than once you can choose any occurrence and append it to the result.
Return _the result string after sorting_ `s` _with this algorithm_.
**Example 1:**
**Input:** s = "aaaabbbbcccc "
**Output:** "abccbaabccba "
**Explanation:** After steps 1, 2 and 3 of the first iteration, result = "abc "
After steps 4, 5 and 6 of the first iteration, result = "abccba "
First iteration is done. Now s = "aabbcc " and we go back to step 1
After steps 1, 2 and 3 of the second iteration, result = "abccbaabc "
After steps 4, 5 and 6 of the second iteration, result = "abccbaabccba "
**Example 2:**
**Input:** s = "rat "
**Output:** "art "
**Explanation:** The word "rat " becomes "art " after re-ordering it with the mentioned algorithm.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | After replacing each even by zero and every odd by one can we use prefix sum to find answer ? Can we use two pointers to count number of sub-arrays ? Can we store indices of odd numbers and for each k indices count number of sub-arrays contains them ? |
[Python 3] Simple Clean code, beats >98% speed. | increasing-decreasing-string | 0 | 1 | Strategy : \n1. Maintain a counter/dictionary of all characters\n2. Maintain a list of sorted characters\n3. Everytime a character is chosen from the dictionary its count is reduced, if it becomes zero the dictionary key is removed\n4. Iterate over this list in ascending and descending order alternatively, adding elements to the result string, unitl the dictionary is not empty\n```\nclass Solution:\n def sortString(self, s: str) -> str:\n \n res = \'\'\n counter = dict(collections.Counter(s))\n chars = sorted(list(set(s)))\n \n while(counter):\n for char in chars:\n if char in counter:\n res += char\n counter[char] -= 1\n if counter[char] == 0:\n del counter[char]\n for char in reversed(chars):\n if char in counter:\n res += char\n counter[char] -= 1\n if counter[char] == 0:\n del counter[char]\n \n return res\n``` | 5 | You are given a string `s`. Reorder the string using the following algorithm:
1. Pick the **smallest** character from `s` and **append** it to the result.
2. Pick the **smallest** character from `s` which is greater than the last appended character to the result and **append** it.
3. Repeat step 2 until you cannot pick more characters.
4. Pick the **largest** character from `s` and **append** it to the result.
5. Pick the **largest** character from `s` which is smaller than the last appended character to the result and **append** it.
6. Repeat step 5 until you cannot pick more characters.
7. Repeat the steps from 1 to 6 until you pick all characters from `s`.
In each step, If the smallest or the largest character appears more than once you can choose any occurrence and append it to the result.
Return _the result string after sorting_ `s` _with this algorithm_.
**Example 1:**
**Input:** s = "aaaabbbbcccc "
**Output:** "abccbaabccba "
**Explanation:** After steps 1, 2 and 3 of the first iteration, result = "abc "
After steps 4, 5 and 6 of the first iteration, result = "abccba "
First iteration is done. Now s = "aabbcc " and we go back to step 1
After steps 1, 2 and 3 of the second iteration, result = "abccbaabc "
After steps 4, 5 and 6 of the second iteration, result = "abccbaabccba "
**Example 2:**
**Input:** s = "rat "
**Output:** "art "
**Explanation:** The word "rat " becomes "art " after re-ordering it with the mentioned algorithm.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | After replacing each even by zero and every odd by one can we use prefix sum to find answer ? Can we use two pointers to count number of sub-arrays ? Can we store indices of odd numbers and for each k indices count number of sub-arrays contains them ? |
[Python/Python 3] hashmap easy-understand solution!!! Beats 97% | increasing-decreasing-string | 0 | 1 | ```\nclass Solution(object):\n def sortString(self, s):\n dict = {}\n for s1 in s:\n dict[s1] = dict.get(s1, 0)+1\n list1 = sorted(list(set(s)))\n \n result = \'\'\n while len(result) < len(s):\n for l in list1:\n if l in dict and dict[l] != 0:\n result += l\n dict[l] -= 1\n \n for l in list1[::-1]:\n if l in dict and dict[l] != 0:\n result += l\n dict[l] -= 1\n \n return result | 1 | You are given a string `s`. Reorder the string using the following algorithm:
1. Pick the **smallest** character from `s` and **append** it to the result.
2. Pick the **smallest** character from `s` which is greater than the last appended character to the result and **append** it.
3. Repeat step 2 until you cannot pick more characters.
4. Pick the **largest** character from `s` and **append** it to the result.
5. Pick the **largest** character from `s` which is smaller than the last appended character to the result and **append** it.
6. Repeat step 5 until you cannot pick more characters.
7. Repeat the steps from 1 to 6 until you pick all characters from `s`.
In each step, If the smallest or the largest character appears more than once you can choose any occurrence and append it to the result.
Return _the result string after sorting_ `s` _with this algorithm_.
**Example 1:**
**Input:** s = "aaaabbbbcccc "
**Output:** "abccbaabccba "
**Explanation:** After steps 1, 2 and 3 of the first iteration, result = "abc "
After steps 4, 5 and 6 of the first iteration, result = "abccba "
First iteration is done. Now s = "aabbcc " and we go back to step 1
After steps 1, 2 and 3 of the second iteration, result = "abccbaabc "
After steps 4, 5 and 6 of the second iteration, result = "abccbaabccba "
**Example 2:**
**Input:** s = "rat "
**Output:** "art "
**Explanation:** The word "rat " becomes "art " after re-ordering it with the mentioned algorithm.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | After replacing each even by zero and every odd by one can we use prefix sum to find answer ? Can we use two pointers to count number of sub-arrays ? Can we store indices of odd numbers and for each k indices count number of sub-arrays contains them ? |
[Python] solution in O(n) time and O(1) space explained | find-the-longest-substring-containing-vowels-in-even-counts | 0 | 1 | We can use 5 bits to represent the parity of the number of occurrences of vowels. For example, we can use 0/1 for even/odd numbers, then if we have 4a, 3e, 2i, 1o, 0u, the representation would be 01010. As we scan through the array, we can update the representation in O(1) time by using the XOR operation, and then store the index where every different representation first appeared. When we encounter a representation, say 01010 again at index `j`, we can look back on the index `i` where 01010 first appeared, and we know that the substring from `i` to `j` must be a valid string, and it is the longest valid substring that ends at `j`.\n```python\ndef findTheLongestSubstring(self, s: str) -> int:\n vowels = {\'a\': 1, \'e\': 2, \'i\': 4, \'o\': 8, \'u\': 16}\n d, n, r = {0: -1}, 0, 0\n for i, c in enumerate(s):\n if c in vowels:\n n ^= vowels[c]\n if n not in d:\n d[n] = i\n else:\n r = max(r, i - d[n])\n return r\n```\nVote up if you find this helpful, thanks! | 77 | Given the string `s`, return the size of the longest substring containing each vowel an even number of times. That is, 'a', 'e', 'i', 'o', and 'u' must appear an even number of times.
**Example 1:**
**Input:** s = "eleetminicoworoep "
**Output:** 13
**Explanation:** The longest substring is "leetminicowor " which contains two each of the vowels: **e**, **i** and **o** and zero of the vowels: **a** and **u**.
**Example 2:**
**Input:** s = "leetcodeisgreat "
**Output:** 5
**Explanation:** The longest substring is "leetc " which contains two e's.
**Example 3:**
**Input:** s = "bcbcbc "
**Output:** 6
**Explanation:** In this case, the given string "bcbcbc " is the longest because all vowels: **a**, **e**, **i**, **o** and **u** appear zero times.
**Constraints:**
* `1 <= s.length <= 5 x 10^5`
* `s` contains only lowercase English letters.
It is the empty string, or It can be written as AB (A concatenated with B), where A and B are valid strings, or It can be written as (A), where A is a valid string. | Each prefix of a balanced parentheses has a number of open parentheses greater or equal than closed parentheses, similar idea with each suffix. Check the array from left to right, remove characters that do not meet the property mentioned above, same idea in backward way. |
[Python] solution in O(n) time and O(1) space explained | find-the-longest-substring-containing-vowels-in-even-counts | 0 | 1 | We can use 5 bits to represent the parity of the number of occurrences of vowels. For example, we can use 0/1 for even/odd numbers, then if we have 4a, 3e, 2i, 1o, 0u, the representation would be 01010. As we scan through the array, we can update the representation in O(1) time by using the XOR operation, and then store the index where every different representation first appeared. When we encounter a representation, say 01010 again at index `j`, we can look back on the index `i` where 01010 first appeared, and we know that the substring from `i` to `j` must be a valid string, and it is the longest valid substring that ends at `j`.\n```python\ndef findTheLongestSubstring(self, s: str) -> int:\n vowels = {\'a\': 1, \'e\': 2, \'i\': 4, \'o\': 8, \'u\': 16}\n d, n, r = {0: -1}, 0, 0\n for i, c in enumerate(s):\n if c in vowels:\n n ^= vowels[c]\n if n not in d:\n d[n] = i\n else:\n r = max(r, i - d[n])\n return r\n```\nVote up if you find this helpful, thanks! | 77 | There is a row of `m` houses in a small city, each house must be painted with one of the `n` colors (labeled from `1` to `n`), some houses that have been painted last summer should not be painted again.
A neighborhood is a maximal group of continuous houses that are painted with the same color.
* For example: `houses = [1,2,2,3,3,2,1,1]` contains `5` neighborhoods `[{1}, {2,2}, {3,3}, {2}, {1,1}]`.
Given an array `houses`, an `m x n` matrix `cost` and an integer `target` where:
* `houses[i]`: is the color of the house `i`, and `0` if the house is not painted yet.
* `cost[i][j]`: is the cost of paint the house `i` with the color `j + 1`.
Return _the minimum cost of painting all the remaining houses in such a way that there are exactly_ `target` _neighborhoods_. If it is not possible, return `-1`.
**Example 1:**
**Input:** houses = \[0,0,0,0,0\], cost = \[\[1,10\],\[10,1\],\[10,1\],\[1,10\],\[5,1\]\], m = 5, n = 2, target = 3
**Output:** 9
**Explanation:** Paint houses of this way \[1,2,2,1,1\]
This array contains target = 3 neighborhoods, \[{1}, {2,2}, {1,1}\].
Cost of paint all houses (1 + 1 + 1 + 1 + 5) = 9.
**Example 2:**
**Input:** houses = \[0,2,1,2,0\], cost = \[\[1,10\],\[10,1\],\[10,1\],\[1,10\],\[5,1\]\], m = 5, n = 2, target = 3
**Output:** 11
**Explanation:** Some houses are already painted, Paint the houses of this way \[2,2,1,2,2\]
This array contains target = 3 neighborhoods, \[{2,2}, {1}, {2,2}\].
Cost of paint the first and last house (10 + 1) = 11.
**Example 3:**
**Input:** houses = \[3,1,2,3\], cost = \[\[1,1,1\],\[1,1,1\],\[1,1,1\],\[1,1,1\]\], m = 4, n = 3, target = 3
**Output:** -1
**Explanation:** Houses are already painted with a total of 4 neighborhoods \[{3},{1},{2},{3}\] different of target = 3.
**Constraints:**
* `m == houses.length == cost.length`
* `n == cost[i].length`
* `1 <= m <= 100`
* `1 <= n <= 20`
* `1 <= target <= m`
* `0 <= houses[i] <= n`
* `1 <= cost[i][j] <= 104` | Represent the counts (odd or even) of vowels with a bitmask. Precompute the prefix xor for the bitmask of vowels and then get the longest valid substring. |
Python 3 || 8 lines, bit mask, w/example || T/M: 91% / 69% | find-the-longest-substring-containing-vowels-in-even-counts | 0 | 1 | ```\nclass Solution:\n def findTheLongestSubstring(self, s: str) -> int:\n # Example: \'leetcodoe\'\n d = defaultdict(int)\n v = {\'a\':0,\'e\':1,\'i\':2,\'o\':3,\'u\':4,} # i ch n ans d\n n, ans, d[0] = 0, 0, -1 # \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\n # 0 l 00000 1 {0:-1}\n for i, ch in enumerate(s): # 1 e 00010 1 {0:-1, 2:1}}\n if ch in \'aeiou\': n ^= (1<<v[ch]) # 2 e 00000 3 {0:-1, 2:1}}\n # 3 t 00000 4 {0:-1, 2:1}}\n if n in d: ans = max(ans, i - d[n]) # 4 c 00000 5 {0:-1, 2:1, 8:5}\n else: d[n] = i # 5 o 01000 5 {0:-1, 2:1, 8:5}\n # 6 d 01000 5 {0:-1, 2:1, 8:5}\n return ans # 7 o 00000 8 {0:-1, 2:1, 8:5}\n # 8 e 00010 8 {0:-1, 2:1, 8:5}\n # / |||||\n # return \'uoiea\'\n```\n[https://leetcode.com/problems/find-the-longest-substring-containing-vowels-in-even-counts/submissions/868729915/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*). | 8 | Given the string `s`, return the size of the longest substring containing each vowel an even number of times. That is, 'a', 'e', 'i', 'o', and 'u' must appear an even number of times.
**Example 1:**
**Input:** s = "eleetminicoworoep "
**Output:** 13
**Explanation:** The longest substring is "leetminicowor " which contains two each of the vowels: **e**, **i** and **o** and zero of the vowels: **a** and **u**.
**Example 2:**
**Input:** s = "leetcodeisgreat "
**Output:** 5
**Explanation:** The longest substring is "leetc " which contains two e's.
**Example 3:**
**Input:** s = "bcbcbc "
**Output:** 6
**Explanation:** In this case, the given string "bcbcbc " is the longest because all vowels: **a**, **e**, **i**, **o** and **u** appear zero times.
**Constraints:**
* `1 <= s.length <= 5 x 10^5`
* `s` contains only lowercase English letters.
It is the empty string, or It can be written as AB (A concatenated with B), where A and B are valid strings, or It can be written as (A), where A is a valid string. | Each prefix of a balanced parentheses has a number of open parentheses greater or equal than closed parentheses, similar idea with each suffix. Check the array from left to right, remove characters that do not meet the property mentioned above, same idea in backward way. |
Python 3 || 8 lines, bit mask, w/example || T/M: 91% / 69% | find-the-longest-substring-containing-vowels-in-even-counts | 0 | 1 | ```\nclass Solution:\n def findTheLongestSubstring(self, s: str) -> int:\n # Example: \'leetcodoe\'\n d = defaultdict(int)\n v = {\'a\':0,\'e\':1,\'i\':2,\'o\':3,\'u\':4,} # i ch n ans d\n n, ans, d[0] = 0, 0, -1 # \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\n # 0 l 00000 1 {0:-1}\n for i, ch in enumerate(s): # 1 e 00010 1 {0:-1, 2:1}}\n if ch in \'aeiou\': n ^= (1<<v[ch]) # 2 e 00000 3 {0:-1, 2:1}}\n # 3 t 00000 4 {0:-1, 2:1}}\n if n in d: ans = max(ans, i - d[n]) # 4 c 00000 5 {0:-1, 2:1, 8:5}\n else: d[n] = i # 5 o 01000 5 {0:-1, 2:1, 8:5}\n # 6 d 01000 5 {0:-1, 2:1, 8:5}\n return ans # 7 o 00000 8 {0:-1, 2:1, 8:5}\n # 8 e 00010 8 {0:-1, 2:1, 8:5}\n # / |||||\n # return \'uoiea\'\n```\n[https://leetcode.com/problems/find-the-longest-substring-containing-vowels-in-even-counts/submissions/868729915/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*). | 8 | There is a row of `m` houses in a small city, each house must be painted with one of the `n` colors (labeled from `1` to `n`), some houses that have been painted last summer should not be painted again.
A neighborhood is a maximal group of continuous houses that are painted with the same color.
* For example: `houses = [1,2,2,3,3,2,1,1]` contains `5` neighborhoods `[{1}, {2,2}, {3,3}, {2}, {1,1}]`.
Given an array `houses`, an `m x n` matrix `cost` and an integer `target` where:
* `houses[i]`: is the color of the house `i`, and `0` if the house is not painted yet.
* `cost[i][j]`: is the cost of paint the house `i` with the color `j + 1`.
Return _the minimum cost of painting all the remaining houses in such a way that there are exactly_ `target` _neighborhoods_. If it is not possible, return `-1`.
**Example 1:**
**Input:** houses = \[0,0,0,0,0\], cost = \[\[1,10\],\[10,1\],\[10,1\],\[1,10\],\[5,1\]\], m = 5, n = 2, target = 3
**Output:** 9
**Explanation:** Paint houses of this way \[1,2,2,1,1\]
This array contains target = 3 neighborhoods, \[{1}, {2,2}, {1,1}\].
Cost of paint all houses (1 + 1 + 1 + 1 + 5) = 9.
**Example 2:**
**Input:** houses = \[0,2,1,2,0\], cost = \[\[1,10\],\[10,1\],\[10,1\],\[1,10\],\[5,1\]\], m = 5, n = 2, target = 3
**Output:** 11
**Explanation:** Some houses are already painted, Paint the houses of this way \[2,2,1,2,2\]
This array contains target = 3 neighborhoods, \[{2,2}, {1}, {2,2}\].
Cost of paint the first and last house (10 + 1) = 11.
**Example 3:**
**Input:** houses = \[3,1,2,3\], cost = \[\[1,1,1\],\[1,1,1\],\[1,1,1\],\[1,1,1\]\], m = 4, n = 3, target = 3
**Output:** -1
**Explanation:** Houses are already painted with a total of 4 neighborhoods \[{3},{1},{2},{3}\] different of target = 3.
**Constraints:**
* `m == houses.length == cost.length`
* `n == cost[i].length`
* `1 <= m <= 100`
* `1 <= n <= 20`
* `1 <= target <= m`
* `0 <= houses[i] <= n`
* `1 <= cost[i][j] <= 104` | Represent the counts (odd or even) of vowels with a bitmask. Precompute the prefix xor for the bitmask of vowels and then get the longest valid substring. |
Prefix Sum Classic Solution | find-the-longest-substring-containing-vowels-in-even-counts | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$.\n\n- Space complexity: $$O(n)$$.\n\n# Code\n```\nclass Solution:\n def findTheLongestSubstring(self, s: str) -> int:\n vowels = \'aeiou\'\n pref = {0: -1}\n maxSize = 0\n mask = 0\n for i, ch in enumerate(s):\n if (ind := vowels.find(ch)) != -1:\n mask ^= 1<<ind\n\n if mask in pref:\n maxSize = max(maxSize, i-pref[mask])\n else:\n pref[mask] = i\n\n return maxSize\n``` | 0 | Given the string `s`, return the size of the longest substring containing each vowel an even number of times. That is, 'a', 'e', 'i', 'o', and 'u' must appear an even number of times.
**Example 1:**
**Input:** s = "eleetminicoworoep "
**Output:** 13
**Explanation:** The longest substring is "leetminicowor " which contains two each of the vowels: **e**, **i** and **o** and zero of the vowels: **a** and **u**.
**Example 2:**
**Input:** s = "leetcodeisgreat "
**Output:** 5
**Explanation:** The longest substring is "leetc " which contains two e's.
**Example 3:**
**Input:** s = "bcbcbc "
**Output:** 6
**Explanation:** In this case, the given string "bcbcbc " is the longest because all vowels: **a**, **e**, **i**, **o** and **u** appear zero times.
**Constraints:**
* `1 <= s.length <= 5 x 10^5`
* `s` contains only lowercase English letters.
It is the empty string, or It can be written as AB (A concatenated with B), where A and B are valid strings, or It can be written as (A), where A is a valid string. | Each prefix of a balanced parentheses has a number of open parentheses greater or equal than closed parentheses, similar idea with each suffix. Check the array from left to right, remove characters that do not meet the property mentioned above, same idea in backward way. |
Prefix Sum Classic Solution | find-the-longest-substring-containing-vowels-in-even-counts | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$.\n\n- Space complexity: $$O(n)$$.\n\n# Code\n```\nclass Solution:\n def findTheLongestSubstring(self, s: str) -> int:\n vowels = \'aeiou\'\n pref = {0: -1}\n maxSize = 0\n mask = 0\n for i, ch in enumerate(s):\n if (ind := vowels.find(ch)) != -1:\n mask ^= 1<<ind\n\n if mask in pref:\n maxSize = max(maxSize, i-pref[mask])\n else:\n pref[mask] = i\n\n return maxSize\n``` | 0 | There is a row of `m` houses in a small city, each house must be painted with one of the `n` colors (labeled from `1` to `n`), some houses that have been painted last summer should not be painted again.
A neighborhood is a maximal group of continuous houses that are painted with the same color.
* For example: `houses = [1,2,2,3,3,2,1,1]` contains `5` neighborhoods `[{1}, {2,2}, {3,3}, {2}, {1,1}]`.
Given an array `houses`, an `m x n` matrix `cost` and an integer `target` where:
* `houses[i]`: is the color of the house `i`, and `0` if the house is not painted yet.
* `cost[i][j]`: is the cost of paint the house `i` with the color `j + 1`.
Return _the minimum cost of painting all the remaining houses in such a way that there are exactly_ `target` _neighborhoods_. If it is not possible, return `-1`.
**Example 1:**
**Input:** houses = \[0,0,0,0,0\], cost = \[\[1,10\],\[10,1\],\[10,1\],\[1,10\],\[5,1\]\], m = 5, n = 2, target = 3
**Output:** 9
**Explanation:** Paint houses of this way \[1,2,2,1,1\]
This array contains target = 3 neighborhoods, \[{1}, {2,2}, {1,1}\].
Cost of paint all houses (1 + 1 + 1 + 1 + 5) = 9.
**Example 2:**
**Input:** houses = \[0,2,1,2,0\], cost = \[\[1,10\],\[10,1\],\[10,1\],\[1,10\],\[5,1\]\], m = 5, n = 2, target = 3
**Output:** 11
**Explanation:** Some houses are already painted, Paint the houses of this way \[2,2,1,2,2\]
This array contains target = 3 neighborhoods, \[{2,2}, {1}, {2,2}\].
Cost of paint the first and last house (10 + 1) = 11.
**Example 3:**
**Input:** houses = \[3,1,2,3\], cost = \[\[1,1,1\],\[1,1,1\],\[1,1,1\],\[1,1,1\]\], m = 4, n = 3, target = 3
**Output:** -1
**Explanation:** Houses are already painted with a total of 4 neighborhoods \[{3},{1},{2},{3}\] different of target = 3.
**Constraints:**
* `m == houses.length == cost.length`
* `n == cost[i].length`
* `1 <= m <= 100`
* `1 <= n <= 20`
* `1 <= target <= m`
* `0 <= houses[i] <= n`
* `1 <= cost[i][j] <= 104` | Represent the counts (odd or even) of vowels with a bitmask. Precompute the prefix xor for the bitmask of vowels and then get the longest valid substring. |
O(n) python solution | find-the-longest-substring-containing-vowels-in-even-counts | 0 | 1 | # Intuition\ncalculated xor of everything, if xor is 0 then elements upto that index then we have even vowels and length of the substring will be index + 1 , but there is one another way of finding a substring with even vowels (if xor of elements from 0 to a has xor = y and xor from 0 to b has also xor = y, such that a < b, then elements from index a to b has even number of vowels and their length would be b-a)\n\n# Approach\ni return index + 1 if i had 0 any time, meaning xor of elements from 0 to that index even have vowels and the length of the substring is index + 1, and i stored every other xor in a dictionary and the value had a list containing the first and last occurrence(index) of that xor, as i explained earlier b-a is also a possible substring with even number of vowels.\n\n# Complexity\n- Time complexity:\nsince the vowels are only 5 and the number of combinations that can be made of it and possible xor are also constant the complexity turns out to be O(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findTheLongestSubstring(self, s: str) -> int:\n l={}\n x=0\n #print(len(s))\n m=-1\n for i in range(len(s)):\n if s[i] in [\'a\',\'e\',\'i\',\'o\',\'u\']:\n x^=ord(s[i])\n if x not in l:\n l[x]=[i,-1]\n else:\n l[x][1]=i\n if x==0:\n m=max(m,i+1)\n if l[x][1]!=-1:\n m=max(m,l[x][1]-l[x][0])\n\n \n #print(x,end=",")\n if m==-1:\n return 0\n return m\n\n\n``` | 0 | Given the string `s`, return the size of the longest substring containing each vowel an even number of times. That is, 'a', 'e', 'i', 'o', and 'u' must appear an even number of times.
**Example 1:**
**Input:** s = "eleetminicoworoep "
**Output:** 13
**Explanation:** The longest substring is "leetminicowor " which contains two each of the vowels: **e**, **i** and **o** and zero of the vowels: **a** and **u**.
**Example 2:**
**Input:** s = "leetcodeisgreat "
**Output:** 5
**Explanation:** The longest substring is "leetc " which contains two e's.
**Example 3:**
**Input:** s = "bcbcbc "
**Output:** 6
**Explanation:** In this case, the given string "bcbcbc " is the longest because all vowels: **a**, **e**, **i**, **o** and **u** appear zero times.
**Constraints:**
* `1 <= s.length <= 5 x 10^5`
* `s` contains only lowercase English letters.
It is the empty string, or It can be written as AB (A concatenated with B), where A and B are valid strings, or It can be written as (A), where A is a valid string. | Each prefix of a balanced parentheses has a number of open parentheses greater or equal than closed parentheses, similar idea with each suffix. Check the array from left to right, remove characters that do not meet the property mentioned above, same idea in backward way. |
O(n) python solution | find-the-longest-substring-containing-vowels-in-even-counts | 0 | 1 | # Intuition\ncalculated xor of everything, if xor is 0 then elements upto that index then we have even vowels and length of the substring will be index + 1 , but there is one another way of finding a substring with even vowels (if xor of elements from 0 to a has xor = y and xor from 0 to b has also xor = y, such that a < b, then elements from index a to b has even number of vowels and their length would be b-a)\n\n# Approach\ni return index + 1 if i had 0 any time, meaning xor of elements from 0 to that index even have vowels and the length of the substring is index + 1, and i stored every other xor in a dictionary and the value had a list containing the first and last occurrence(index) of that xor, as i explained earlier b-a is also a possible substring with even number of vowels.\n\n# Complexity\n- Time complexity:\nsince the vowels are only 5 and the number of combinations that can be made of it and possible xor are also constant the complexity turns out to be O(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findTheLongestSubstring(self, s: str) -> int:\n l={}\n x=0\n #print(len(s))\n m=-1\n for i in range(len(s)):\n if s[i] in [\'a\',\'e\',\'i\',\'o\',\'u\']:\n x^=ord(s[i])\n if x not in l:\n l[x]=[i,-1]\n else:\n l[x][1]=i\n if x==0:\n m=max(m,i+1)\n if l[x][1]!=-1:\n m=max(m,l[x][1]-l[x][0])\n\n \n #print(x,end=",")\n if m==-1:\n return 0\n return m\n\n\n``` | 0 | There is a row of `m` houses in a small city, each house must be painted with one of the `n` colors (labeled from `1` to `n`), some houses that have been painted last summer should not be painted again.
A neighborhood is a maximal group of continuous houses that are painted with the same color.
* For example: `houses = [1,2,2,3,3,2,1,1]` contains `5` neighborhoods `[{1}, {2,2}, {3,3}, {2}, {1,1}]`.
Given an array `houses`, an `m x n` matrix `cost` and an integer `target` where:
* `houses[i]`: is the color of the house `i`, and `0` if the house is not painted yet.
* `cost[i][j]`: is the cost of paint the house `i` with the color `j + 1`.
Return _the minimum cost of painting all the remaining houses in such a way that there are exactly_ `target` _neighborhoods_. If it is not possible, return `-1`.
**Example 1:**
**Input:** houses = \[0,0,0,0,0\], cost = \[\[1,10\],\[10,1\],\[10,1\],\[1,10\],\[5,1\]\], m = 5, n = 2, target = 3
**Output:** 9
**Explanation:** Paint houses of this way \[1,2,2,1,1\]
This array contains target = 3 neighborhoods, \[{1}, {2,2}, {1,1}\].
Cost of paint all houses (1 + 1 + 1 + 1 + 5) = 9.
**Example 2:**
**Input:** houses = \[0,2,1,2,0\], cost = \[\[1,10\],\[10,1\],\[10,1\],\[1,10\],\[5,1\]\], m = 5, n = 2, target = 3
**Output:** 11
**Explanation:** Some houses are already painted, Paint the houses of this way \[2,2,1,2,2\]
This array contains target = 3 neighborhoods, \[{2,2}, {1}, {2,2}\].
Cost of paint the first and last house (10 + 1) = 11.
**Example 3:**
**Input:** houses = \[3,1,2,3\], cost = \[\[1,1,1\],\[1,1,1\],\[1,1,1\],\[1,1,1\]\], m = 4, n = 3, target = 3
**Output:** -1
**Explanation:** Houses are already painted with a total of 4 neighborhoods \[{3},{1},{2},{3}\] different of target = 3.
**Constraints:**
* `m == houses.length == cost.length`
* `n == cost[i].length`
* `1 <= m <= 100`
* `1 <= n <= 20`
* `1 <= target <= m`
* `0 <= houses[i] <= n`
* `1 <= cost[i][j] <= 104` | Represent the counts (odd or even) of vowels with a bitmask. Precompute the prefix xor for the bitmask of vowels and then get the longest valid substring. |
Image Explanation🏆- [Easy & Complete Intuition] - C++/Java/Python | longest-zigzag-path-in-a-binary-tree | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Longest ZigZag Path in a Binary Tree` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n\n\n\n\n\n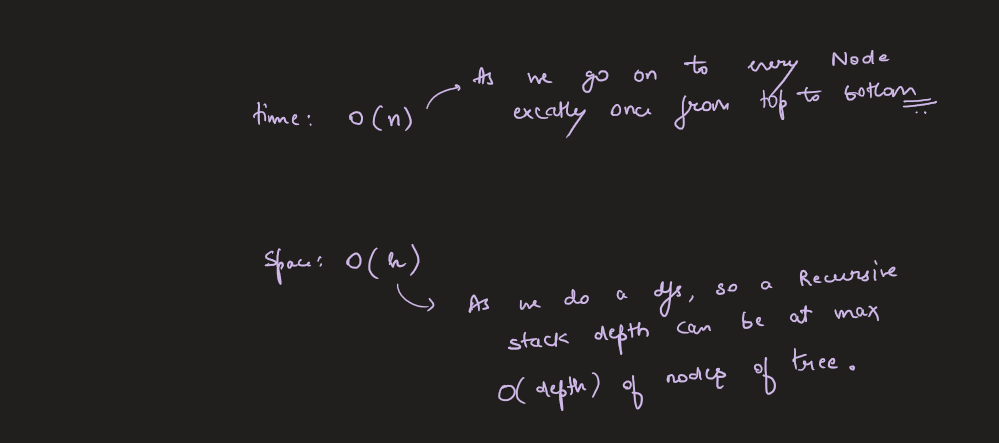\n\n\n# Code\n```C++ []\nclass Solution {\n public:\n int maxLength=0;\n\n void solve(TreeNode* root,int dir,int currLength){\n if(!root) return;\n maxLength=max(maxLength,currLength);\n solve(root->left,0,dir?currLength+1:1);\n solve(root->right,1,dir?1:currLength+1);\n }\n\n int longestZigZag(TreeNode* root) {\n solve(root,0,0);\n solve(root,1,0);\n return maxLength;\n }\n};\n```\n```Java []\nclass Solution {\n public int maxLength=0;\n public void solve(TreeNode root,int dir,int currLength){\n if(root==null) return;\n maxLength=Math.max(maxLength,currLength);\n if(dir==1){\n solve(root.left,0,currLength+1);\n solve(root.right,1,1);\n }\n else{\n solve(root.right,1,currLength+1);\n solve(root.left,0,1);\n }\n }\n\n public int longestZigZag(TreeNode root) {\n solve(root,0,0);\n solve(root,1,0);\n return maxLength;\n }\n}\n```\n```Python []\nclass Solution:\n def longestZigZag(self, root: Optional[TreeNode]) -> int:\n self.maxLength = 0\n def solve(node, deep, dir):\n self.maxLength = max(self.maxLength, deep)\n\n if node.left is not None:\n solve(node.left, deep+1,\'left\') if dir != \'left\' else solve(node.left, 1, \'left\')\n if node.right is not None:\n solve(node.right, deep+1, \'right\') if dir != \'right\' else solve(node.right, 1, \'right\')\n solve(root, 0, \'\')\n return self.maxLength\n```\n | 91 | You are given the `root` of a binary tree.
A ZigZag path for a binary tree is defined as follow:
* Choose **any** node in the binary tree and a direction (right or left).
* If the current direction is right, move to the right child of the current node; otherwise, move to the left child.
* Change the direction from right to left or from left to right.
* Repeat the second and third steps until you can't move in the tree.
Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).
Return _the longest **ZigZag** path contained in that tree_.
**Example 1:**
**Input:** root = \[1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1\]
**Output:** 3
**Explanation:** Longest ZigZag path in blue nodes (right -> left -> right).
**Example 2:**
**Input:** root = \[1,1,1,null,1,null,null,1,1,null,1\]
**Output:** 4
**Explanation:** Longest ZigZag path in blue nodes (left -> right -> left -> right).
**Example 3:**
**Input:** root = \[1\]
**Output:** 0
**Constraints:**
* The number of nodes in the tree is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 100` | Eq. ax+by=1 has solution x, y if gcd(a,b) = 1. Can you generalize the formula?. Check Bézout's lemma. |
[Python] Efficient and Easy Depth-First Search (DFS) Solution | longest-zigzag-path-in-a-binary-tree | 0 | 1 | # Approach\nTo solve this problem, we can use the DFS (Depth-First Search) approach while keeping track of the previous traversal. When the previous traversal goes to the left, the next traversal to the right can make use of the previous height. However, if the next traversal goes to the left again, its height will start from 0 because it no longer follows the zigzag pattern. \n\n# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\nclass Solution:\n def dfs(self, tree, h=0, state=None):\n if tree is None:\n self.max_h = max(h, self.max_h)\n return\n \n self.dfs(tree.left, h+1 if state=="right" else 0, "left")\n self.dfs(tree.right, h+1 if state=="left" else 0, "right")\n \n\n def longestZigZag(self, root: Optional[TreeNode]) -> int:\n self.max_h = 0\n self.dfs(root)\n return self.max_h\n``` | 1 | You are given the `root` of a binary tree.
A ZigZag path for a binary tree is defined as follow:
* Choose **any** node in the binary tree and a direction (right or left).
* If the current direction is right, move to the right child of the current node; otherwise, move to the left child.
* Change the direction from right to left or from left to right.
* Repeat the second and third steps until you can't move in the tree.
Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).
Return _the longest **ZigZag** path contained in that tree_.
**Example 1:**
**Input:** root = \[1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1\]
**Output:** 3
**Explanation:** Longest ZigZag path in blue nodes (right -> left -> right).
**Example 2:**
**Input:** root = \[1,1,1,null,1,null,null,1,1,null,1\]
**Output:** 4
**Explanation:** Longest ZigZag path in blue nodes (left -> right -> left -> right).
**Example 3:**
**Input:** root = \[1\]
**Output:** 0
**Constraints:**
* The number of nodes in the tree is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 100` | Eq. ax+by=1 has solution x, y if gcd(a,b) = 1. Can you generalize the formula?. Check Bézout's lemma. |
[Python] Easy traversal with explanation | maximum-sum-bst-in-binary-tree | 0 | 1 | **Idea**\nFor each subtree, we return 4 elements.\n1. the status of this subtree, `1` means it\'s empty, `2` means it\'s a BST, `0` means it\'s not a BST\n2. size of this subtree (we only care about size of BST though)\n3. the minimal value in this subtree\n4. the maximal value in this subtree\n\nThen we only need to make sure for every BST\n- both of its children are BST\n- the right bound of its left child is smaller than `root.val`\n- the left bound of its right child is larger than `root.val`\n\n**Complexity**\nTime: `O(N)`\nSpace: `O(logN)` for function calls, worst case `O(N)` if the given tree is not balanced\n\n**Python 3**\n```\nclass Solution:\n def maxSumBST(self, root: TreeNode) -> int:\n res = 0\n def traverse(root):\n \'\'\'return status_of_bst, size_of_bst, left_bound, right_bound\'\'\'\n nonlocal res\n if not root: return 1, 0, None, None # this subtree is empty\n \n ls, l, ll, lr = traverse(root.left)\n rs, r, rl, rr = traverse(root.right)\n \n if ((ls == 2 and lr < root.val) or ls == 1) and ((rs == 2 and rl > root.val) or rs == 1):\n\t\t # this subtree is a BST\n size = root.val + l + r\n res = max(res, size)\n return 2, size, (ll if ll is not None else root.val), (rr if rr is not None else root.val)\n return 0, None, None, None # this subtree is not a BST\n \n traverse(root)\n return res\n``` | 41 | Given a **binary tree** `root`, return _the maximum sum of all keys of **any** sub-tree which is also a Binary Search Tree (BST)_.
Assume a BST is defined as follows:
* The left subtree of a node contains only nodes with keys **less than** the node's key.
* The right subtree of a node contains only nodes with keys **greater than** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[1,4,3,2,4,2,5,null,null,null,null,null,null,4,6\]
**Output:** 20
**Explanation:** Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.
**Example 2:**
**Input:** root = \[4,3,null,1,2\]
**Output:** 2
**Explanation:** Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.
**Example 3:**
**Input:** root = \[-4,-2,-5\]
**Output:** 0
**Explanation:** All values are negatives. Return an empty BST.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 4 * 104]`.
* `-4 * 104 <= Node.val <= 4 * 104` | null |
[Python] Easy traversal with explanation | maximum-sum-bst-in-binary-tree | 0 | 1 | **Idea**\nFor each subtree, we return 4 elements.\n1. the status of this subtree, `1` means it\'s empty, `2` means it\'s a BST, `0` means it\'s not a BST\n2. size of this subtree (we only care about size of BST though)\n3. the minimal value in this subtree\n4. the maximal value in this subtree\n\nThen we only need to make sure for every BST\n- both of its children are BST\n- the right bound of its left child is smaller than `root.val`\n- the left bound of its right child is larger than `root.val`\n\n**Complexity**\nTime: `O(N)`\nSpace: `O(logN)` for function calls, worst case `O(N)` if the given tree is not balanced\n\n**Python 3**\n```\nclass Solution:\n def maxSumBST(self, root: TreeNode) -> int:\n res = 0\n def traverse(root):\n \'\'\'return status_of_bst, size_of_bst, left_bound, right_bound\'\'\'\n nonlocal res\n if not root: return 1, 0, None, None # this subtree is empty\n \n ls, l, ll, lr = traverse(root.left)\n rs, r, rl, rr = traverse(root.right)\n \n if ((ls == 2 and lr < root.val) or ls == 1) and ((rs == 2 and rl > root.val) or rs == 1):\n\t\t # this subtree is a BST\n size = root.val + l + r\n res = max(res, size)\n return 2, size, (ll if ll is not None else root.val), (rr if rr is not None else root.val)\n return 0, None, None, None # this subtree is not a BST\n \n traverse(root)\n return res\n``` | 41 | You are given an integer array `prices` where `prices[i]` is the price of the `ith` item in a shop.
There is a special discount for items in the shop. If you buy the `ith` item, then you will receive a discount equivalent to `prices[j]` where `j` is the minimum index such that `j > i` and `prices[j] <= prices[i]`. Otherwise, you will not receive any discount at all.
Return an integer array `answer` where `answer[i]` is the final price you will pay for the `ith` item of the shop, considering the special discount.
**Example 1:**
**Input:** prices = \[8,4,6,2,3\]
**Output:** \[4,2,4,2,3\]
**Explanation:**
For item 0 with price\[0\]=8 you will receive a discount equivalent to prices\[1\]=4, therefore, the final price you will pay is 8 - 4 = 4.
For item 1 with price\[1\]=4 you will receive a discount equivalent to prices\[3\]=2, therefore, the final price you will pay is 4 - 2 = 2.
For item 2 with price\[2\]=6 you will receive a discount equivalent to prices\[3\]=2, therefore, the final price you will pay is 6 - 2 = 4.
For items 3 and 4 you will not receive any discount at all.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** \[1,2,3,4,5\]
**Explanation:** In this case, for all items, you will not receive any discount at all.
**Example 3:**
**Input:** prices = \[10,1,1,6\]
**Output:** \[9,0,1,6\]
**Constraints:**
* `1 <= prices.length <= 500`
* `1 <= prices[i] <= 1000`
The left subtree of a node contains only nodes with keys less than the node's key. The right subtree of a node contains only nodes with keys greater than the node's key. Both the left and right subtrees must also be binary search trees. | Create a datastructure with 4 parameters: (sum, isBST, maxLeft, minLeft). In each node compute theses parameters, following the conditions of a Binary Search Tree. |
Python || Easy || Bottom up approach | maximum-sum-bst-in-binary-tree | 0 | 1 | ```\nclass NodeValue:\n def __init__(self, minNode, maxNode, Sum):\n self.maxNode = maxNode\n self.minNode = minNode\n self.Sum = Sum\n\nclass Solution:\n def largestBstHelper(self, node):\n if not node:\n return NodeValue(float(\'inf\'), float(\'-inf\'), 0)\n\n left = self.largestBstHelper(node.left)\n right = self.largestBstHelper(node.right)\n\n if left.maxNode < node.val and node.val < right.minNode:\n currSum=left.Sum+ right.Sum + node.val\n self.maxSum=max(self.maxSum,currSum)\n return NodeValue(min(node.val, left.minNode), max(node.val, right.maxNode),currSum)\n\n return NodeValue(float(\'-inf\'), float(\'inf\'), max(left.Sum, right.Sum))\n \n def maxSumBST(self, root: Optional[TreeNode]) -> int:\n self.maxSum=0\n ans=self.largestBstHelper(root).Sum \n return self.maxSum\n```\n**An upvote will be encouraging** | 5 | Given a **binary tree** `root`, return _the maximum sum of all keys of **any** sub-tree which is also a Binary Search Tree (BST)_.
Assume a BST is defined as follows:
* The left subtree of a node contains only nodes with keys **less than** the node's key.
* The right subtree of a node contains only nodes with keys **greater than** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[1,4,3,2,4,2,5,null,null,null,null,null,null,4,6\]
**Output:** 20
**Explanation:** Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.
**Example 2:**
**Input:** root = \[4,3,null,1,2\]
**Output:** 2
**Explanation:** Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.
**Example 3:**
**Input:** root = \[-4,-2,-5\]
**Output:** 0
**Explanation:** All values are negatives. Return an empty BST.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 4 * 104]`.
* `-4 * 104 <= Node.val <= 4 * 104` | null |
Python || Easy || Bottom up approach | maximum-sum-bst-in-binary-tree | 0 | 1 | ```\nclass NodeValue:\n def __init__(self, minNode, maxNode, Sum):\n self.maxNode = maxNode\n self.minNode = minNode\n self.Sum = Sum\n\nclass Solution:\n def largestBstHelper(self, node):\n if not node:\n return NodeValue(float(\'inf\'), float(\'-inf\'), 0)\n\n left = self.largestBstHelper(node.left)\n right = self.largestBstHelper(node.right)\n\n if left.maxNode < node.val and node.val < right.minNode:\n currSum=left.Sum+ right.Sum + node.val\n self.maxSum=max(self.maxSum,currSum)\n return NodeValue(min(node.val, left.minNode), max(node.val, right.maxNode),currSum)\n\n return NodeValue(float(\'-inf\'), float(\'inf\'), max(left.Sum, right.Sum))\n \n def maxSumBST(self, root: Optional[TreeNode]) -> int:\n self.maxSum=0\n ans=self.largestBstHelper(root).Sum \n return self.maxSum\n```\n**An upvote will be encouraging** | 5 | You are given an integer array `prices` where `prices[i]` is the price of the `ith` item in a shop.
There is a special discount for items in the shop. If you buy the `ith` item, then you will receive a discount equivalent to `prices[j]` where `j` is the minimum index such that `j > i` and `prices[j] <= prices[i]`. Otherwise, you will not receive any discount at all.
Return an integer array `answer` where `answer[i]` is the final price you will pay for the `ith` item of the shop, considering the special discount.
**Example 1:**
**Input:** prices = \[8,4,6,2,3\]
**Output:** \[4,2,4,2,3\]
**Explanation:**
For item 0 with price\[0\]=8 you will receive a discount equivalent to prices\[1\]=4, therefore, the final price you will pay is 8 - 4 = 4.
For item 1 with price\[1\]=4 you will receive a discount equivalent to prices\[3\]=2, therefore, the final price you will pay is 4 - 2 = 2.
For item 2 with price\[2\]=6 you will receive a discount equivalent to prices\[3\]=2, therefore, the final price you will pay is 6 - 2 = 4.
For items 3 and 4 you will not receive any discount at all.
**Example 2:**
**Input:** prices = \[1,2,3,4,5\]
**Output:** \[1,2,3,4,5\]
**Explanation:** In this case, for all items, you will not receive any discount at all.
**Example 3:**
**Input:** prices = \[10,1,1,6\]
**Output:** \[9,0,1,6\]
**Constraints:**
* `1 <= prices.length <= 500`
* `1 <= prices[i] <= 1000`
The left subtree of a node contains only nodes with keys less than the node's key. The right subtree of a node contains only nodes with keys greater than the node's key. Both the left and right subtrees must also be binary search trees. | Create a datastructure with 4 parameters: (sum, isBST, maxLeft, minLeft). In each node compute theses parameters, following the conditions of a Binary Search Tree. |
Simple Code $$ Easy to Understand | generate-a-string-with-characters-that-have-odd-counts | 0 | 1 | # Code\n```\nclass Solution:\n def generateTheString(self, n: int) -> str:\n res = ""\n if n%2 != 0:\n return "a"*n\n res = "a"*(n-1)\n return res+"b"\n``` | 1 | Given an integer `n`, _return a string with `n` characters such that each character in such string occurs **an odd number of times**_.
The returned string must contain only lowercase English letters. If there are multiples valid strings, return **any** of them.
**Example 1:**
**Input:** n = 4
**Output:** "pppz "
**Explanation:** "pppz " is a valid string since the character 'p' occurs three times and the character 'z' occurs once. Note that there are many other valid strings such as "ohhh " and "love ".
**Example 2:**
**Input:** n = 2
**Output:** "xy "
**Explanation:** "xy " is a valid string since the characters 'x' and 'y' occur once. Note that there are many other valid strings such as "ag " and "ur ".
**Example 3:**
**Input:** n = 7
**Output:** "holasss "
**Constraints:**
* `1 <= n <= 500` | 1. (Binary Search) For each row do a binary search to find the leftmost one on that row and update the answer. 2. (Optimal Approach) Imagine there is a pointer p(x, y) starting from top right corner. p can only move left or down. If the value at p is 0, move down. If the value at p is 1, move left. Try to figure out the correctness and time complexity of this algorithm. |
Python one line simple solution | generate-a-string-with-characters-that-have-odd-counts | 0 | 1 | **Python :**\n\n```\ndef generateTheString(self, n: int) -> str:\n\treturn "a" * n if n % 2 else "a" * (n - 1) + "b"\n```\n\n**Like it ? please upvote !** | 9 | Given an integer `n`, _return a string with `n` characters such that each character in such string occurs **an odd number of times**_.
The returned string must contain only lowercase English letters. If there are multiples valid strings, return **any** of them.
**Example 1:**
**Input:** n = 4
**Output:** "pppz "
**Explanation:** "pppz " is a valid string since the character 'p' occurs three times and the character 'z' occurs once. Note that there are many other valid strings such as "ohhh " and "love ".
**Example 2:**
**Input:** n = 2
**Output:** "xy "
**Explanation:** "xy " is a valid string since the characters 'x' and 'y' occur once. Note that there are many other valid strings such as "ag " and "ur ".
**Example 3:**
**Input:** n = 7
**Output:** "holasss "
**Constraints:**
* `1 <= n <= 500` | 1. (Binary Search) For each row do a binary search to find the leftmost one on that row and update the answer. 2. (Optimal Approach) Imagine there is a pointer p(x, y) starting from top right corner. p can only move left or down. If the value at p is 0, move down. If the value at p is 1, move left. Try to figure out the correctness and time complexity of this algorithm. |
One Liner Python3 | generate-a-string-with-characters-that-have-odd-counts | 0 | 1 | \n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def generateTheString(self, n: int) -> str:\n \n return \'a\' * n if n % 2 != 0 else \'a\' * (n-1) + \'b\'\n\n \n``` | 2 | Given an integer `n`, _return a string with `n` characters such that each character in such string occurs **an odd number of times**_.
The returned string must contain only lowercase English letters. If there are multiples valid strings, return **any** of them.
**Example 1:**
**Input:** n = 4
**Output:** "pppz "
**Explanation:** "pppz " is a valid string since the character 'p' occurs three times and the character 'z' occurs once. Note that there are many other valid strings such as "ohhh " and "love ".
**Example 2:**
**Input:** n = 2
**Output:** "xy "
**Explanation:** "xy " is a valid string since the characters 'x' and 'y' occur once. Note that there are many other valid strings such as "ag " and "ur ".
**Example 3:**
**Input:** n = 7
**Output:** "holasss "
**Constraints:**
* `1 <= n <= 500` | 1. (Binary Search) For each row do a binary search to find the leftmost one on that row and update the answer. 2. (Optimal Approach) Imagine there is a pointer p(x, y) starting from top right corner. p can only move left or down. If the value at p is 0, move down. If the value at p is 1, move left. Try to figure out the correctness and time complexity of this algorithm. |
Python || Easy || 94.60% Faster ||One Line Solution | generate-a-string-with-characters-that-have-odd-counts | 0 | 1 | ```\nclass Solution:\n def generateTheString(self, n: int) -> str:\n return \'a\'*(n-1)+\'b\' if n%2==0 else \'a\'*n\n```\n\n**An upvote will be encouraging** | 2 | Given an integer `n`, _return a string with `n` characters such that each character in such string occurs **an odd number of times**_.
The returned string must contain only lowercase English letters. If there are multiples valid strings, return **any** of them.
**Example 1:**
**Input:** n = 4
**Output:** "pppz "
**Explanation:** "pppz " is a valid string since the character 'p' occurs three times and the character 'z' occurs once. Note that there are many other valid strings such as "ohhh " and "love ".
**Example 2:**
**Input:** n = 2
**Output:** "xy "
**Explanation:** "xy " is a valid string since the characters 'x' and 'y' occur once. Note that there are many other valid strings such as "ag " and "ur ".
**Example 3:**
**Input:** n = 7
**Output:** "holasss "
**Constraints:**
* `1 <= n <= 500` | 1. (Binary Search) For each row do a binary search to find the leftmost one on that row and update the answer. 2. (Optimal Approach) Imagine there is a pointer p(x, y) starting from top right corner. p can only move left or down. If the value at p is 0, move down. If the value at p is 1, move left. Try to figure out the correctness and time complexity of this algorithm. |
Keep track of the largest bit | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Intuition\nTo solve this problem we need to note one intricacy that will always hold true\n* Each bit only appears in `flips` once. \n* Therefore, if bit x is on (one based), then it is only possible to be "Prefix-Aligned" if we are on flip x (also one based). \n\nWe can now keep track of the largest bit, and the number of flips. After each flip we can check if it is possible to be "Prefix-Aligned"\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* To keep the book keeping simple, we will count the number of flips starting at 1\n* `largest_bit` will keep track of the largest bit\n* `count` will keep track of the number of times we have been "Prefix-Aligned"\n\n# Complexity\n- Time complexity `O(|flips|)`:\nSingle pass through all the flips\n\n- Space complexity `O(1)`:\nA few constant variables\n\n# Code\n```\n# Keep track of the largest bit that is on\n\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n largest_bit = 0\n count = 0\n for i, bit in enumerate(flips, 1):\n largest_bit = max(largest_bit, bit)\n if largest_bit == i:\n count += 1\n return count\n``` | 4 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
Keep track of the largest bit | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Intuition\nTo solve this problem we need to note one intricacy that will always hold true\n* Each bit only appears in `flips` once. \n* Therefore, if bit x is on (one based), then it is only possible to be "Prefix-Aligned" if we are on flip x (also one based). \n\nWe can now keep track of the largest bit, and the number of flips. After each flip we can check if it is possible to be "Prefix-Aligned"\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* To keep the book keeping simple, we will count the number of flips starting at 1\n* `largest_bit` will keep track of the largest bit\n* `count` will keep track of the number of times we have been "Prefix-Aligned"\n\n# Complexity\n- Time complexity `O(|flips|)`:\nSingle pass through all the flips\n\n- Space complexity `O(1)`:\nA few constant variables\n\n# Code\n```\n# Keep track of the largest bit that is on\n\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n largest_bit = 0\n count = 0\n for i, bit in enumerate(flips, 1):\n largest_bit = max(largest_bit, bit)\n if largest_bit == i:\n count += 1\n return count\n``` | 4 | You are given an array of **unique** integers `salary` where `salary[i]` is the salary of the `ith` employee.
Return _the average salary of employees excluding the minimum and maximum salary_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** salary = \[4000,3000,1000,2000\]
**Output:** 2500.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 4000 respectively.
Average salary excluding minimum and maximum salary is (2000+3000) / 2 = 2500
**Example 2:**
**Input:** salary = \[1000,2000,3000\]
**Output:** 2000.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 3000 respectively.
Average salary excluding minimum and maximum salary is (2000) / 1 = 2000
**Constraints:**
* `3 <= salary.length <= 100`
* `1000 <= salary[i] <= 106`
* All the integers of `salary` are **unique**. | If in the step x all bulb shines then bulbs 1,2,3,..,x should shines too. |
Python 3 || 6 lines, w/ explanation || T/M: 90% / 96% | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | Here\'s the plan:\n- The binary string is prefix-aligned if and only if the flips comprise a set of consecutive integers beginning with one (`123` is valid, `234` or `125` is not)\n- The indices will always comprise a set of consecutive integers beginning with zero.\n- The binary string is prefix-aligned after `k` flips if and only if `sum (i+1) = sum (flips[:i+1])` for `i < k`.\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n\n ans = fSum = iSum = 0\n\n for i,flip in enumerate(flips):\n\n fSum+= flip\n iSum+= i+1\n\n ans+= (iSum==fSum)\n\n return ans\n\n```\n[https://leetcode.com/problems/number-of-times-binary-string-is-prefix-aligned/submissions/855688402/](http://)\n\n\nI could be wrong, but I think that time is *O*(*N*) and space is *O*(1). | 5 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
Python 3 || 6 lines, w/ explanation || T/M: 90% / 96% | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | Here\'s the plan:\n- The binary string is prefix-aligned if and only if the flips comprise a set of consecutive integers beginning with one (`123` is valid, `234` or `125` is not)\n- The indices will always comprise a set of consecutive integers beginning with zero.\n- The binary string is prefix-aligned after `k` flips if and only if `sum (i+1) = sum (flips[:i+1])` for `i < k`.\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n\n ans = fSum = iSum = 0\n\n for i,flip in enumerate(flips):\n\n fSum+= flip\n iSum+= i+1\n\n ans+= (iSum==fSum)\n\n return ans\n\n```\n[https://leetcode.com/problems/number-of-times-binary-string-is-prefix-aligned/submissions/855688402/](http://)\n\n\nI could be wrong, but I think that time is *O*(*N*) and space is *O*(1). | 5 | You are given an array of **unique** integers `salary` where `salary[i]` is the salary of the `ith` employee.
Return _the average salary of employees excluding the minimum and maximum salary_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** salary = \[4000,3000,1000,2000\]
**Output:** 2500.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 4000 respectively.
Average salary excluding minimum and maximum salary is (2000+3000) / 2 = 2500
**Example 2:**
**Input:** salary = \[1000,2000,3000\]
**Output:** 2000.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 3000 respectively.
Average salary excluding minimum and maximum salary is (2000) / 1 = 2000
**Constraints:**
* `3 <= salary.length <= 100`
* `1000 <= salary[i] <= 106`
* All the integers of `salary` are **unique**. | If in the step x all bulb shines then bulbs 1,2,3,..,x should shines too. |
Python3 solution O(n) time and O(1) space complexity | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | ```\nclass Solution:\n def numTimesAllBlue(self, light: List[int]) -> int:\n max = count = 0\n for i in range(len(light)):\n if max < light[i]:\n max = light[i]\n if max == i + 1:\n count += 1\n return count\n```\n**If you like this solution, please upvote for this** | 4 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
Python3 solution O(n) time and O(1) space complexity | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | ```\nclass Solution:\n def numTimesAllBlue(self, light: List[int]) -> int:\n max = count = 0\n for i in range(len(light)):\n if max < light[i]:\n max = light[i]\n if max == i + 1:\n count += 1\n return count\n```\n**If you like this solution, please upvote for this** | 4 | You are given an array of **unique** integers `salary` where `salary[i]` is the salary of the `ith` employee.
Return _the average salary of employees excluding the minimum and maximum salary_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** salary = \[4000,3000,1000,2000\]
**Output:** 2500.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 4000 respectively.
Average salary excluding minimum and maximum salary is (2000+3000) / 2 = 2500
**Example 2:**
**Input:** salary = \[1000,2000,3000\]
**Output:** 2000.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 3000 respectively.
Average salary excluding minimum and maximum salary is (2000) / 1 = 2000
**Constraints:**
* `3 <= salary.length <= 100`
* `1000 <= salary[i] <= 106`
* All the integers of `salary` are **unique**. | If in the step x all bulb shines then bulbs 1,2,3,..,x should shines too. |
Intuitive Math Approach O(N) time, O(1) space | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Intuition\nYou basically need to check if the numbers are continuous up until point i. (e.g. 1,2,3,4,5..., i for all i). You don\'t actually need to track the length since as you iterate through x it\'ll always be the same. The only time the function is continuous is if the sum of up to element x is the same as the sum of your indexes (since we know that the repeated cites don\'t switch off the bit from 1 to 0). \n\nFor example in the test scenario:\n**At i = 1**\na = 3\nb = 1,\n**At i = 2**\na = 2 + 3\nb = 1 + 2,\n**At i = 3,**\na = 2 + 3 + 4\nb = 1 + 2 + 3\n**At i = 4,**\na = 2 + 3 + 4 + 1\nb = 1 + 2 + 3 + 4\n....\n\nThis holds since adding element x at index i will never decrease the sum. If they are equal, add 1.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n out = 0\n a = 0\n b = 0\n for i,x in enumerate(flips):\n a += x\n b += i+1\n if a == b:\n out += 1\n return out\n``` | 0 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
Intuitive Math Approach O(N) time, O(1) space | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Intuition\nYou basically need to check if the numbers are continuous up until point i. (e.g. 1,2,3,4,5..., i for all i). You don\'t actually need to track the length since as you iterate through x it\'ll always be the same. The only time the function is continuous is if the sum of up to element x is the same as the sum of your indexes (since we know that the repeated cites don\'t switch off the bit from 1 to 0). \n\nFor example in the test scenario:\n**At i = 1**\na = 3\nb = 1,\n**At i = 2**\na = 2 + 3\nb = 1 + 2,\n**At i = 3,**\na = 2 + 3 + 4\nb = 1 + 2 + 3\n**At i = 4,**\na = 2 + 3 + 4 + 1\nb = 1 + 2 + 3 + 4\n....\n\nThis holds since adding element x at index i will never decrease the sum. If they are equal, add 1.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n out = 0\n a = 0\n b = 0\n for i,x in enumerate(flips):\n a += x\n b += i+1\n if a == b:\n out += 1\n return out\n``` | 0 | You are given an array of **unique** integers `salary` where `salary[i]` is the salary of the `ith` employee.
Return _the average salary of employees excluding the minimum and maximum salary_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** salary = \[4000,3000,1000,2000\]
**Output:** 2500.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 4000 respectively.
Average salary excluding minimum and maximum salary is (2000+3000) / 2 = 2500
**Example 2:**
**Input:** salary = \[1000,2000,3000\]
**Output:** 2000.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 3000 respectively.
Average salary excluding minimum and maximum salary is (2000) / 1 = 2000
**Constraints:**
* `3 <= salary.length <= 100`
* `1000 <= salary[i] <= 106`
* All the integers of `salary` are **unique**. | If in the step x all bulb shines then bulbs 1,2,3,..,x should shines too. |
One-line python solution | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n return sum(cnt == k for k,cnt in zip(range(1, len(flips)+1), accumulate(flips, max)))\n``` | 0 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
One-line python solution | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n return sum(cnt == k for k,cnt in zip(range(1, len(flips)+1), accumulate(flips, max)))\n``` | 0 | You are given an array of **unique** integers `salary` where `salary[i]` is the salary of the `ith` employee.
Return _the average salary of employees excluding the minimum and maximum salary_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** salary = \[4000,3000,1000,2000\]
**Output:** 2500.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 4000 respectively.
Average salary excluding minimum and maximum salary is (2000+3000) / 2 = 2500
**Example 2:**
**Input:** salary = \[1000,2000,3000\]
**Output:** 2000.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 3000 respectively.
Average salary excluding minimum and maximum salary is (2000) / 1 = 2000
**Constraints:**
* `3 <= salary.length <= 100`
* `1000 <= salary[i] <= 106`
* All the integers of `salary` are **unique**. | If in the step x all bulb shines then bulbs 1,2,3,..,x should shines too. |
Easy O(n) math + prefix sum in python 3 | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCheck if prefix sum is equal to the range sum from 0 to length of prefix array sum(range(i+2)) -> sum(0, 1, ... i+1). This way there is no need to keep track of which numbers are missing since each range sum is distinct. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nKeep a running sum or a prefix sum and add 1 at each index if sum(range(index+2)) == running sum. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n tot = 0\n cnt = 0\n for i, f in enumerate(flips):\n tot += f\n if tot == (i+1)*(i+2)//2:\n cnt += 1\n return cnt\n```\nOne-liner (because why not)\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n return sum((i+1)*(i+2)//2 == f for i, f in enumerate(accumulate(flips)))\n``` | 0 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
Easy O(n) math + prefix sum in python 3 | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCheck if prefix sum is equal to the range sum from 0 to length of prefix array sum(range(i+2)) -> sum(0, 1, ... i+1). This way there is no need to keep track of which numbers are missing since each range sum is distinct. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nKeep a running sum or a prefix sum and add 1 at each index if sum(range(index+2)) == running sum. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n tot = 0\n cnt = 0\n for i, f in enumerate(flips):\n tot += f\n if tot == (i+1)*(i+2)//2:\n cnt += 1\n return cnt\n```\nOne-liner (because why not)\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n return sum((i+1)*(i+2)//2 == f for i, f in enumerate(accumulate(flips)))\n``` | 0 | You are given an array of **unique** integers `salary` where `salary[i]` is the salary of the `ith` employee.
Return _the average salary of employees excluding the minimum and maximum salary_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** salary = \[4000,3000,1000,2000\]
**Output:** 2500.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 4000 respectively.
Average salary excluding minimum and maximum salary is (2000+3000) / 2 = 2500
**Example 2:**
**Input:** salary = \[1000,2000,3000\]
**Output:** 2000.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 3000 respectively.
Average salary excluding minimum and maximum salary is (2000) / 1 = 2000
**Constraints:**
* `3 <= salary.length <= 100`
* `1000 <= salary[i] <= 106`
* All the integers of `salary` are **unique**. | If in the step x all bulb shines then bulbs 1,2,3,..,x should shines too. |
clever O(N) python solution | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n \'\'\'\n at every point, we need to keep track of the first 1, the last 1, the first 0.\n conditions for a prefix-aligned string are:\n first and last 1 are before the first 0.\n \'\'\'\n f_one, l_one, f_zero = float("inf"), -1, 0\n ct = 0\n for i, x in enumerate(flips):\n f_one, l_one = min(x, f_one), max(x, l_one)\n if f_one == 1 and l_one == i + 1:\n f_zero = l_one + 1\n if f_one < f_zero and l_one < f_zero:\n ct += 1\n #print(f_one, l_one, f_zero)\n return ct\n``` | 0 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
clever O(N) python solution | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n \'\'\'\n at every point, we need to keep track of the first 1, the last 1, the first 0.\n conditions for a prefix-aligned string are:\n first and last 1 are before the first 0.\n \'\'\'\n f_one, l_one, f_zero = float("inf"), -1, 0\n ct = 0\n for i, x in enumerate(flips):\n f_one, l_one = min(x, f_one), max(x, l_one)\n if f_one == 1 and l_one == i + 1:\n f_zero = l_one + 1\n if f_one < f_zero and l_one < f_zero:\n ct += 1\n #print(f_one, l_one, f_zero)\n return ct\n``` | 0 | You are given an array of **unique** integers `salary` where `salary[i]` is the salary of the `ith` employee.
Return _the average salary of employees excluding the minimum and maximum salary_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** salary = \[4000,3000,1000,2000\]
**Output:** 2500.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 4000 respectively.
Average salary excluding minimum and maximum salary is (2000+3000) / 2 = 2500
**Example 2:**
**Input:** salary = \[1000,2000,3000\]
**Output:** 2000.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 3000 respectively.
Average salary excluding minimum and maximum salary is (2000) / 1 = 2000
**Constraints:**
* `3 <= salary.length <= 100`
* `1000 <= salary[i] <= 106`
* All the integers of `salary` are **unique**. | If in the step x all bulb shines then bulbs 1,2,3,..,x should shines too. |
O(n) solution | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n rs = 0\n n = len(flips)\n a = [0] * n\n ans = 0\n\n for i in range(n):\n idx = flips[i] - 1\n a[idx] = 1\n\n rs += a[i]\n\n if idx < i:\n rs += 1\n \n if rs == i + 1:\n ans += 1\n\n return ans\n\n``` | 0 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
O(n) solution | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n rs = 0\n n = len(flips)\n a = [0] * n\n ans = 0\n\n for i in range(n):\n idx = flips[i] - 1\n a[idx] = 1\n\n rs += a[i]\n\n if idx < i:\n rs += 1\n \n if rs == i + 1:\n ans += 1\n\n return ans\n\n``` | 0 | You are given an array of **unique** integers `salary` where `salary[i]` is the salary of the `ith` employee.
Return _the average salary of employees excluding the minimum and maximum salary_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** salary = \[4000,3000,1000,2000\]
**Output:** 2500.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 4000 respectively.
Average salary excluding minimum and maximum salary is (2000+3000) / 2 = 2500
**Example 2:**
**Input:** salary = \[1000,2000,3000\]
**Output:** 2000.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 3000 respectively.
Average salary excluding minimum and maximum salary is (2000) / 1 = 2000
**Constraints:**
* `3 <= salary.length <= 100`
* `1000 <= salary[i] <= 106`
* All the integers of `salary` are **unique**. | If in the step x all bulb shines then bulbs 1,2,3,..,x should shines too. |
Python3 Concise straight forward solution | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n \n n=len(flips)\n ans=mask=curr=0\n \n for i,f in enumerate(flips):\n curr+=(1<<(n-i-1))\n mask=mask^(1<<(n-f))\n if curr==mask:\n ans+=1\n \n return ans\n``` | 0 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
Python3 Concise straight forward solution | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n \n n=len(flips)\n ans=mask=curr=0\n \n for i,f in enumerate(flips):\n curr+=(1<<(n-i-1))\n mask=mask^(1<<(n-f))\n if curr==mask:\n ans+=1\n \n return ans\n``` | 0 | You are given an array of **unique** integers `salary` where `salary[i]` is the salary of the `ith` employee.
Return _the average salary of employees excluding the minimum and maximum salary_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** salary = \[4000,3000,1000,2000\]
**Output:** 2500.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 4000 respectively.
Average salary excluding minimum and maximum salary is (2000+3000) / 2 = 2500
**Example 2:**
**Input:** salary = \[1000,2000,3000\]
**Output:** 2000.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 3000 respectively.
Average salary excluding minimum and maximum salary is (2000) / 1 = 2000
**Constraints:**
* `3 <= salary.length <= 100`
* `1000 <= salary[i] <= 106`
* All the integers of `salary` are **unique**. | If in the step x all bulb shines then bulbs 1,2,3,..,x should shines too. |
[Python] Solution Easy to Understand | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Code\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n n = len(flips)\n l = 1e9\n r = 0\n res = 0\n flipOne = False\n for i in range(n):\n if flips[i] == 1: flipOne = True\n if flips[i] < l:\n l = flips[i]\n if flips[i] > r:\n r = flips[i]\n if (r - l + 1) == i + 1 and flipOne:\n res += 1\n return res\n``` | 0 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
[Python] Solution Easy to Understand | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Code\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n n = len(flips)\n l = 1e9\n r = 0\n res = 0\n flipOne = False\n for i in range(n):\n if flips[i] == 1: flipOne = True\n if flips[i] < l:\n l = flips[i]\n if flips[i] > r:\n r = flips[i]\n if (r - l + 1) == i + 1 and flipOne:\n res += 1\n return res\n``` | 0 | You are given an array of **unique** integers `salary` where `salary[i]` is the salary of the `ith` employee.
Return _the average salary of employees excluding the minimum and maximum salary_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** salary = \[4000,3000,1000,2000\]
**Output:** 2500.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 4000 respectively.
Average salary excluding minimum and maximum salary is (2000+3000) / 2 = 2500
**Example 2:**
**Input:** salary = \[1000,2000,3000\]
**Output:** 2000.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 3000 respectively.
Average salary excluding minimum and maximum salary is (2000) / 1 = 2000
**Constraints:**
* `3 <= salary.length <= 100`
* `1000 <= salary[i] <= 106`
* All the integers of `salary` are **unique**. | If in the step x all bulb shines then bulbs 1,2,3,..,x should shines too. |
Python - Bitwise | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Intuition\nSet bit of flip[i], and check [1, i] are all ones by masking.\n\n# Complexity\n- Time complexity: $$O(n)$$ \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$ \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n n = len(flips)\n count = n-1\n mask = 1 << count\n initial = 0\n res = 0\n for idx in range(1, n+1):\n b = flips[idx - 1]\n initial |= (1 << (n - b))\n # print("{0:b}".format(initial))\n # print("{0:b}".format(mask))\n # print("{0:b}".format(initial & mask))\n # print("----")\n if initial & mask == mask:\n res += 1\n count -= 1\n if count > 0:\n mask |= 1 << count\n return res\n``` | 0 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
Python - Bitwise | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Intuition\nSet bit of flip[i], and check [1, i] are all ones by masking.\n\n# Complexity\n- Time complexity: $$O(n)$$ \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$ \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numTimesAllBlue(self, flips: List[int]) -> int:\n n = len(flips)\n count = n-1\n mask = 1 << count\n initial = 0\n res = 0\n for idx in range(1, n+1):\n b = flips[idx - 1]\n initial |= (1 << (n - b))\n # print("{0:b}".format(initial))\n # print("{0:b}".format(mask))\n # print("{0:b}".format(initial & mask))\n # print("----")\n if initial & mask == mask:\n res += 1\n count -= 1\n if count > 0:\n mask |= 1 << count\n return res\n``` | 0 | You are given an array of **unique** integers `salary` where `salary[i]` is the salary of the `ith` employee.
Return _the average salary of employees excluding the minimum and maximum salary_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** salary = \[4000,3000,1000,2000\]
**Output:** 2500.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 4000 respectively.
Average salary excluding minimum and maximum salary is (2000+3000) / 2 = 2500
**Example 2:**
**Input:** salary = \[1000,2000,3000\]
**Output:** 2000.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 3000 respectively.
Average salary excluding minimum and maximum salary is (2000) / 1 = 2000
**Constraints:**
* `3 <= salary.length <= 100`
* `1000 <= salary[i] <= 106`
* All the integers of `salary` are **unique**. | If in the step x all bulb shines then bulbs 1,2,3,..,x should shines too. |
EASY AND COINCISE SOLUTION BEATS 91,37% OF RUNTIME ✅ | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n\n# Code\n```\nclass Solution(object):\n def numTimesAllBlue(self, flips):\n\n pivot = flips[0]\n ans = 1 if pivot == 1 else 0\n left = 0\n \n for i in range(1, len(flips)):\n \n if flips[i] > pivot:\n pivot = flips[i]\n\n left += 1\n \n if left == pivot - 1: \n ans += 1 \n\n return ans\n\n \n\n \n``` | 0 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
EASY AND COINCISE SOLUTION BEATS 91,37% OF RUNTIME ✅ | number-of-times-binary-string-is-prefix-aligned | 0 | 1 | # Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n\n# Code\n```\nclass Solution(object):\n def numTimesAllBlue(self, flips):\n\n pivot = flips[0]\n ans = 1 if pivot == 1 else 0\n left = 0\n \n for i in range(1, len(flips)):\n \n if flips[i] > pivot:\n pivot = flips[i]\n\n left += 1\n \n if left == pivot - 1: \n ans += 1 \n\n return ans\n\n \n\n \n``` | 0 | You are given an array of **unique** integers `salary` where `salary[i]` is the salary of the `ith` employee.
Return _the average salary of employees excluding the minimum and maximum salary_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** salary = \[4000,3000,1000,2000\]
**Output:** 2500.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 4000 respectively.
Average salary excluding minimum and maximum salary is (2000+3000) / 2 = 2500
**Example 2:**
**Input:** salary = \[1000,2000,3000\]
**Output:** 2000.00000
**Explanation:** Minimum salary and maximum salary are 1000 and 3000 respectively.
Average salary excluding minimum and maximum salary is (2000) / 1 = 2000
**Constraints:**
* `3 <= salary.length <= 100`
* `1000 <= salary[i] <= 106`
* All the integers of `salary` are **unique**. | If in the step x all bulb shines then bulbs 1,2,3,..,x should shines too. |
Simple and optimal python3 solution | time-needed-to-inform-all-employees | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nfrom collections import defaultdict\n\nclass Solution:\n def numOfMinutes(self, n: int, headID: int, manager: List[int], informTime: List[int]) -> int:\n vs = defaultdict(list)\n for i, u in enumerate(manager):\n vs[u].append(i)\n\n def recursive(u):\n result = 0\n for v in vs[u]:\n result = max(result, recursive(v))\n return result + informTime[u]\n \n return recursive(headID)\n\n``` | 1 | A company has `n` employees with a unique ID for each employee from `0` to `n - 1`. The head of the company is the one with `headID`.
Each employee has one direct manager given in the `manager` array where `manager[i]` is the direct manager of the `i-th` employee, `manager[headID] = -1`. Also, it is guaranteed that the subordination relationships have a tree structure.
The head of the company wants to inform all the company employees of an urgent piece of news. He will inform his direct subordinates, and they will inform their subordinates, and so on until all employees know about the urgent news.
The `i-th` employee needs `informTime[i]` minutes to inform all of his direct subordinates (i.e., After informTime\[i\] minutes, all his direct subordinates can start spreading the news).
Return _the number of minutes_ needed to inform all the employees about the urgent news.
**Example 1:**
**Input:** n = 1, headID = 0, manager = \[-1\], informTime = \[0\]
**Output:** 0
**Explanation:** The head of the company is the only employee in the company.
**Example 2:**
**Input:** n = 6, headID = 2, manager = \[2,2,-1,2,2,2\], informTime = \[0,0,1,0,0,0\]
**Output:** 1
**Explanation:** The head of the company with id = 2 is the direct manager of all the employees in the company and needs 1 minute to inform them all.
The tree structure of the employees in the company is shown.
**Constraints:**
* `1 <= n <= 105`
* `0 <= headID < n`
* `manager.length == n`
* `0 <= manager[i] < n`
* `manager[headID] == -1`
* `informTime.length == n`
* `0 <= informTime[i] <= 1000`
* `informTime[i] == 0` if employee `i` has no subordinates.
* It is **guaranteed** that all the employees can be informed. | null |
Simple and optimal python3 solution | time-needed-to-inform-all-employees | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nfrom collections import defaultdict\n\nclass Solution:\n def numOfMinutes(self, n: int, headID: int, manager: List[int], informTime: List[int]) -> int:\n vs = defaultdict(list)\n for i, u in enumerate(manager):\n vs[u].append(i)\n\n def recursive(u):\n result = 0\n for v in vs[u]:\n result = max(result, recursive(v))\n return result + informTime[u]\n \n return recursive(headID)\n\n``` | 1 | You are given two positive integers `n` and `k`. A factor of an integer `n` is defined as an integer `i` where `n % i == 0`.
Consider a list of all factors of `n` sorted in **ascending order**, return _the_ `kth` _factor_ in this list or return `-1` if `n` has less than `k` factors.
**Example 1:**
**Input:** n = 12, k = 3
**Output:** 3
**Explanation:** Factors list is \[1, 2, 3, 4, 6, 12\], the 3rd factor is 3.
**Example 2:**
**Input:** n = 7, k = 2
**Output:** 7
**Explanation:** Factors list is \[1, 7\], the 2nd factor is 7.
**Example 3:**
**Input:** n = 4, k = 4
**Output:** -1
**Explanation:** Factors list is \[1, 2, 4\], there is only 3 factors. We should return -1.
**Constraints:**
* `1 <= k <= n <= 1000`
**Follow up:**
Could you solve this problem in less than O(n) complexity? | The company can be represented as a tree, headID is always the root. Store for each node the time needed to be informed of the news. Answer is the max time a leaf node needs to be informed. |
Beating 97.72% Python Easiest Solution | time-needed-to-inform-all-employees | 0 | 1 | \n\n\n# Code\n```\nclass Solution:\n def numOfMinutes(self, n: int, headID: int, manager: List[int], informTime: List[int]) -> int: \n def calculateTime(n: int) -> int:\n if manager[n] != -1:\n informTime[n] += calculateTime(manager[n])\n manager[n] = -1\n return informTime[n]\n for idx in range(len(manager)):\n calculateTime(idx)\n return max(informTime)\n``` | 1 | A company has `n` employees with a unique ID for each employee from `0` to `n - 1`. The head of the company is the one with `headID`.
Each employee has one direct manager given in the `manager` array where `manager[i]` is the direct manager of the `i-th` employee, `manager[headID] = -1`. Also, it is guaranteed that the subordination relationships have a tree structure.
The head of the company wants to inform all the company employees of an urgent piece of news. He will inform his direct subordinates, and they will inform their subordinates, and so on until all employees know about the urgent news.
The `i-th` employee needs `informTime[i]` minutes to inform all of his direct subordinates (i.e., After informTime\[i\] minutes, all his direct subordinates can start spreading the news).
Return _the number of minutes_ needed to inform all the employees about the urgent news.
**Example 1:**
**Input:** n = 1, headID = 0, manager = \[-1\], informTime = \[0\]
**Output:** 0
**Explanation:** The head of the company is the only employee in the company.
**Example 2:**
**Input:** n = 6, headID = 2, manager = \[2,2,-1,2,2,2\], informTime = \[0,0,1,0,0,0\]
**Output:** 1
**Explanation:** The head of the company with id = 2 is the direct manager of all the employees in the company and needs 1 minute to inform them all.
The tree structure of the employees in the company is shown.
**Constraints:**
* `1 <= n <= 105`
* `0 <= headID < n`
* `manager.length == n`
* `0 <= manager[i] < n`
* `manager[headID] == -1`
* `informTime.length == n`
* `0 <= informTime[i] <= 1000`
* `informTime[i] == 0` if employee `i` has no subordinates.
* It is **guaranteed** that all the employees can be informed. | null |
Beating 97.72% Python Easiest Solution | time-needed-to-inform-all-employees | 0 | 1 | \n\n\n# Code\n```\nclass Solution:\n def numOfMinutes(self, n: int, headID: int, manager: List[int], informTime: List[int]) -> int: \n def calculateTime(n: int) -> int:\n if manager[n] != -1:\n informTime[n] += calculateTime(manager[n])\n manager[n] = -1\n return informTime[n]\n for idx in range(len(manager)):\n calculateTime(idx)\n return max(informTime)\n``` | 1 | You are given two positive integers `n` and `k`. A factor of an integer `n` is defined as an integer `i` where `n % i == 0`.
Consider a list of all factors of `n` sorted in **ascending order**, return _the_ `kth` _factor_ in this list or return `-1` if `n` has less than `k` factors.
**Example 1:**
**Input:** n = 12, k = 3
**Output:** 3
**Explanation:** Factors list is \[1, 2, 3, 4, 6, 12\], the 3rd factor is 3.
**Example 2:**
**Input:** n = 7, k = 2
**Output:** 7
**Explanation:** Factors list is \[1, 7\], the 2nd factor is 7.
**Example 3:**
**Input:** n = 4, k = 4
**Output:** -1
**Explanation:** Factors list is \[1, 2, 4\], there is only 3 factors. We should return -1.
**Constraints:**
* `1 <= k <= n <= 1000`
**Follow up:**
Could you solve this problem in less than O(n) complexity? | The company can be represented as a tree, headID is always the root. Store for each node the time needed to be informed of the news. Answer is the max time a leaf node needs to be informed. |
✨🔥 Python: BFS Solution 🔥✨ | time-needed-to-inform-all-employees | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nBFS\n\n# Complexity\n- Time complexity: O(V)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(V)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numOfMinutes(self, n: int, headID: int, manager: List[int], informTime: List[int]) -> int:\n if n == 1: return 0\n\n adj = {i: [] for i in range(n)}\n\n for i in range(n):\n if i != headID:\n adj[manager[i]].append(i)\n \n que = deque()\n que.append((headID, 0))\n vis = [0] * n\n vis[headID] = 1\n ans = 0\n while que:\n node, time = que.popleft()\n ans = max(ans, time)\n for nod in adj[node]:\n if vis[nod] == 0:\n que.append((nod, time + informTime[node]))\n vis[nod] = 1\n \n return ans\n```\n# UPVOTE Please!! | 1 | A company has `n` employees with a unique ID for each employee from `0` to `n - 1`. The head of the company is the one with `headID`.
Each employee has one direct manager given in the `manager` array where `manager[i]` is the direct manager of the `i-th` employee, `manager[headID] = -1`. Also, it is guaranteed that the subordination relationships have a tree structure.
The head of the company wants to inform all the company employees of an urgent piece of news. He will inform his direct subordinates, and they will inform their subordinates, and so on until all employees know about the urgent news.
The `i-th` employee needs `informTime[i]` minutes to inform all of his direct subordinates (i.e., After informTime\[i\] minutes, all his direct subordinates can start spreading the news).
Return _the number of minutes_ needed to inform all the employees about the urgent news.
**Example 1:**
**Input:** n = 1, headID = 0, manager = \[-1\], informTime = \[0\]
**Output:** 0
**Explanation:** The head of the company is the only employee in the company.
**Example 2:**
**Input:** n = 6, headID = 2, manager = \[2,2,-1,2,2,2\], informTime = \[0,0,1,0,0,0\]
**Output:** 1
**Explanation:** The head of the company with id = 2 is the direct manager of all the employees in the company and needs 1 minute to inform them all.
The tree structure of the employees in the company is shown.
**Constraints:**
* `1 <= n <= 105`
* `0 <= headID < n`
* `manager.length == n`
* `0 <= manager[i] < n`
* `manager[headID] == -1`
* `informTime.length == n`
* `0 <= informTime[i] <= 1000`
* `informTime[i] == 0` if employee `i` has no subordinates.
* It is **guaranteed** that all the employees can be informed. | null |
✨🔥 Python: BFS Solution 🔥✨ | time-needed-to-inform-all-employees | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nBFS\n\n# Complexity\n- Time complexity: O(V)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(V)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numOfMinutes(self, n: int, headID: int, manager: List[int], informTime: List[int]) -> int:\n if n == 1: return 0\n\n adj = {i: [] for i in range(n)}\n\n for i in range(n):\n if i != headID:\n adj[manager[i]].append(i)\n \n que = deque()\n que.append((headID, 0))\n vis = [0] * n\n vis[headID] = 1\n ans = 0\n while que:\n node, time = que.popleft()\n ans = max(ans, time)\n for nod in adj[node]:\n if vis[nod] == 0:\n que.append((nod, time + informTime[node]))\n vis[nod] = 1\n \n return ans\n```\n# UPVOTE Please!! | 1 | You are given two positive integers `n` and `k`. A factor of an integer `n` is defined as an integer `i` where `n % i == 0`.
Consider a list of all factors of `n` sorted in **ascending order**, return _the_ `kth` _factor_ in this list or return `-1` if `n` has less than `k` factors.
**Example 1:**
**Input:** n = 12, k = 3
**Output:** 3
**Explanation:** Factors list is \[1, 2, 3, 4, 6, 12\], the 3rd factor is 3.
**Example 2:**
**Input:** n = 7, k = 2
**Output:** 7
**Explanation:** Factors list is \[1, 7\], the 2nd factor is 7.
**Example 3:**
**Input:** n = 4, k = 4
**Output:** -1
**Explanation:** Factors list is \[1, 2, 4\], there is only 3 factors. We should return -1.
**Constraints:**
* `1 <= k <= n <= 1000`
**Follow up:**
Could you solve this problem in less than O(n) complexity? | The company can be represented as a tree, headID is always the root. Store for each node the time needed to be informed of the news. Answer is the max time a leaf node needs to be informed. |
✅ 🔥 Python3 || ⚡easy solution | time-needed-to-inform-all-employees | 0 | 1 | \n```\nclass Solution:\n def numOfMinutes(self, n: int, headID: int, manager: List[int], informTime: List[int]) -> int: \n def calculateTime(n: int) -> int:\n if manager[n] != -1:\n informTime[n] += calculateTime(manager[n])\n manager[n] = -1\n return informTime[n]\n \n for idx in range(len(manager)):\n calculateTime(idx)\n \n return max(informTime)\n\n``` | 1 | A company has `n` employees with a unique ID for each employee from `0` to `n - 1`. The head of the company is the one with `headID`.
Each employee has one direct manager given in the `manager` array where `manager[i]` is the direct manager of the `i-th` employee, `manager[headID] = -1`. Also, it is guaranteed that the subordination relationships have a tree structure.
The head of the company wants to inform all the company employees of an urgent piece of news. He will inform his direct subordinates, and they will inform their subordinates, and so on until all employees know about the urgent news.
The `i-th` employee needs `informTime[i]` minutes to inform all of his direct subordinates (i.e., After informTime\[i\] minutes, all his direct subordinates can start spreading the news).
Return _the number of minutes_ needed to inform all the employees about the urgent news.
**Example 1:**
**Input:** n = 1, headID = 0, manager = \[-1\], informTime = \[0\]
**Output:** 0
**Explanation:** The head of the company is the only employee in the company.
**Example 2:**
**Input:** n = 6, headID = 2, manager = \[2,2,-1,2,2,2\], informTime = \[0,0,1,0,0,0\]
**Output:** 1
**Explanation:** The head of the company with id = 2 is the direct manager of all the employees in the company and needs 1 minute to inform them all.
The tree structure of the employees in the company is shown.
**Constraints:**
* `1 <= n <= 105`
* `0 <= headID < n`
* `manager.length == n`
* `0 <= manager[i] < n`
* `manager[headID] == -1`
* `informTime.length == n`
* `0 <= informTime[i] <= 1000`
* `informTime[i] == 0` if employee `i` has no subordinates.
* It is **guaranteed** that all the employees can be informed. | null |
✅ 🔥 Python3 || ⚡easy solution | time-needed-to-inform-all-employees | 0 | 1 | \n```\nclass Solution:\n def numOfMinutes(self, n: int, headID: int, manager: List[int], informTime: List[int]) -> int: \n def calculateTime(n: int) -> int:\n if manager[n] != -1:\n informTime[n] += calculateTime(manager[n])\n manager[n] = -1\n return informTime[n]\n \n for idx in range(len(manager)):\n calculateTime(idx)\n \n return max(informTime)\n\n``` | 1 | You are given two positive integers `n` and `k`. A factor of an integer `n` is defined as an integer `i` where `n % i == 0`.
Consider a list of all factors of `n` sorted in **ascending order**, return _the_ `kth` _factor_ in this list or return `-1` if `n` has less than `k` factors.
**Example 1:**
**Input:** n = 12, k = 3
**Output:** 3
**Explanation:** Factors list is \[1, 2, 3, 4, 6, 12\], the 3rd factor is 3.
**Example 2:**
**Input:** n = 7, k = 2
**Output:** 7
**Explanation:** Factors list is \[1, 7\], the 2nd factor is 7.
**Example 3:**
**Input:** n = 4, k = 4
**Output:** -1
**Explanation:** Factors list is \[1, 2, 4\], there is only 3 factors. We should return -1.
**Constraints:**
* `1 <= k <= n <= 1000`
**Follow up:**
Could you solve this problem in less than O(n) complexity? | The company can be represented as a tree, headID is always the root. Store for each node the time needed to be informed of the news. Answer is the max time a leaf node needs to be informed. |
Python short and clean. DFS. Functional programming. | time-needed-to-inform-all-employees | 0 | 1 | # Approach\n1. Construct an `WeightedTree` of the form,\n `WeightedTree = (Weight, List of child WeightedTrees)`,\n with managers as parent nodes and employees as child nodes, `inform_time` as `Weight`.\n\n2. Define, `max_path_sum of root = Weight of root + max(max_path_sum of all children)`.\n\n3. Return `max_path_sum` with `head_id` node as root.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def numOfMinutes(self, n: int, head_id: int, manager: list[int], inform_time: list[int]) -> int:\n Weight = int | float\n WeightedTree = tuple[Weight, Iterable[\'WeightedTree\']]\n\n def max_path_sum(tree: WeightedTree) -> Weight:\n return tree[0] + max(map(max_path_sum, tree[1]), default=0)\n\n nodes = defaultdict(lambda: (0, []), {e: (t, []) for e, t in enumerate(inform_time)})\n for e, m in enumerate(manager): nodes[m][1].append(nodes[e])\n \n return max_path_sum(nodes[head_id])\n\n\n``` | 2 | A company has `n` employees with a unique ID for each employee from `0` to `n - 1`. The head of the company is the one with `headID`.
Each employee has one direct manager given in the `manager` array where `manager[i]` is the direct manager of the `i-th` employee, `manager[headID] = -1`. Also, it is guaranteed that the subordination relationships have a tree structure.
The head of the company wants to inform all the company employees of an urgent piece of news. He will inform his direct subordinates, and they will inform their subordinates, and so on until all employees know about the urgent news.
The `i-th` employee needs `informTime[i]` minutes to inform all of his direct subordinates (i.e., After informTime\[i\] minutes, all his direct subordinates can start spreading the news).
Return _the number of minutes_ needed to inform all the employees about the urgent news.
**Example 1:**
**Input:** n = 1, headID = 0, manager = \[-1\], informTime = \[0\]
**Output:** 0
**Explanation:** The head of the company is the only employee in the company.
**Example 2:**
**Input:** n = 6, headID = 2, manager = \[2,2,-1,2,2,2\], informTime = \[0,0,1,0,0,0\]
**Output:** 1
**Explanation:** The head of the company with id = 2 is the direct manager of all the employees in the company and needs 1 minute to inform them all.
The tree structure of the employees in the company is shown.
**Constraints:**
* `1 <= n <= 105`
* `0 <= headID < n`
* `manager.length == n`
* `0 <= manager[i] < n`
* `manager[headID] == -1`
* `informTime.length == n`
* `0 <= informTime[i] <= 1000`
* `informTime[i] == 0` if employee `i` has no subordinates.
* It is **guaranteed** that all the employees can be informed. | null |
Python short and clean. DFS. Functional programming. | time-needed-to-inform-all-employees | 0 | 1 | # Approach\n1. Construct an `WeightedTree` of the form,\n `WeightedTree = (Weight, List of child WeightedTrees)`,\n with managers as parent nodes and employees as child nodes, `inform_time` as `Weight`.\n\n2. Define, `max_path_sum of root = Weight of root + max(max_path_sum of all children)`.\n\n3. Return `max_path_sum` with `head_id` node as root.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def numOfMinutes(self, n: int, head_id: int, manager: list[int], inform_time: list[int]) -> int:\n Weight = int | float\n WeightedTree = tuple[Weight, Iterable[\'WeightedTree\']]\n\n def max_path_sum(tree: WeightedTree) -> Weight:\n return tree[0] + max(map(max_path_sum, tree[1]), default=0)\n\n nodes = defaultdict(lambda: (0, []), {e: (t, []) for e, t in enumerate(inform_time)})\n for e, m in enumerate(manager): nodes[m][1].append(nodes[e])\n \n return max_path_sum(nodes[head_id])\n\n\n``` | 2 | You are given two positive integers `n` and `k`. A factor of an integer `n` is defined as an integer `i` where `n % i == 0`.
Consider a list of all factors of `n` sorted in **ascending order**, return _the_ `kth` _factor_ in this list or return `-1` if `n` has less than `k` factors.
**Example 1:**
**Input:** n = 12, k = 3
**Output:** 3
**Explanation:** Factors list is \[1, 2, 3, 4, 6, 12\], the 3rd factor is 3.
**Example 2:**
**Input:** n = 7, k = 2
**Output:** 7
**Explanation:** Factors list is \[1, 7\], the 2nd factor is 7.
**Example 3:**
**Input:** n = 4, k = 4
**Output:** -1
**Explanation:** Factors list is \[1, 2, 4\], there is only 3 factors. We should return -1.
**Constraints:**
* `1 <= k <= n <= 1000`
**Follow up:**
Could you solve this problem in less than O(n) complexity? | The company can be represented as a tree, headID is always the root. Store for each node the time needed to be informed of the news. Answer is the max time a leaf node needs to be informed. |
Simple Python Solution using BFS | frog-position-after-t-seconds | 0 | 1 | \n# Code\n```\nfrom queue import Queue\n\nclass Solution:\n def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:\n if edges == []:\n if target == 1:return 1\n return 0\n\n d = {}\n for i in edges:\n d[i[0]] = d.get(i[0] , []) + [i[1]]\n d[i[1]] = d.get(i[1] , []) + [i[0]]\n \n visit = [0]*(n+1)\n\n q = Queue() \n q.put([1 , 1])\n\n for dur in range(t):\n \n l = q.qsize()\n for i in range(l):\n temp = q.get()\n\n # Count no.of non-visited nodes\n count = 0\n for ele in d[temp[0]]:\n if visit[ele] == 0: count += 1\n \n if temp[0] == target and count == 0: \n # If the target is reached and if its the end node\n return temp[1]\n \n if visit[temp[0]] != 0: # if already visited\n continue\n \n visit[temp[0]] = 1\n\n for ele in d[temp[0]]:\n if visit[ele] == 0: q.put([ele , temp[1]*(1/count)])\n \n \n l = q.qsize()\n for i in range(l):\n temp = q.get()\n if temp[0] == target:\n return temp[1]\n\n return 0\n``` | 2 | Given an undirected tree consisting of `n` vertices numbered from `1` to `n`. A frog starts jumping from **vertex 1**. In one second, the frog jumps from its current vertex to another **unvisited** vertex if they are directly connected. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices, it jumps randomly to one of them with the same probability. Otherwise, when the frog can not jump to any unvisited vertex, it jumps forever on the same vertex.
The edges of the undirected tree are given in the array `edges`, where `edges[i] = [ai, bi]` means that exists an edge connecting the vertices `ai` and `bi`.
_Return the probability that after `t` seconds the frog is on the vertex `target`._ Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** n = 7, edges = \[\[1,2\],\[1,3\],\[1,7\],\[2,4\],\[2,6\],\[3,5\]\], t = 2, target = 4
**Output:** 0.16666666666666666
**Explanation:** The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 probability to the vertex 2 after **second 1** and then jumping with 1/2 probability to vertex 4 after **second 2**. Thus the probability for the frog is on the vertex 4 after 2 seconds is 1/3 \* 1/2 = 1/6 = 0.16666666666666666.
**Example 2:**
**Input:** n = 7, edges = \[\[1,2\],\[1,3\],\[1,7\],\[2,4\],\[2,6\],\[3,5\]\], t = 1, target = 7
**Output:** 0.3333333333333333
**Explanation:** The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 = 0.3333333333333333 probability to the vertex 7 after **second 1**.
**Constraints:**
* `1 <= n <= 100`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `1 <= ai, bi <= n`
* `1 <= t <= 50`
* `1 <= target <= n` | null |
Simple Python Solution using BFS | frog-position-after-t-seconds | 0 | 1 | \n# Code\n```\nfrom queue import Queue\n\nclass Solution:\n def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:\n if edges == []:\n if target == 1:return 1\n return 0\n\n d = {}\n for i in edges:\n d[i[0]] = d.get(i[0] , []) + [i[1]]\n d[i[1]] = d.get(i[1] , []) + [i[0]]\n \n visit = [0]*(n+1)\n\n q = Queue() \n q.put([1 , 1])\n\n for dur in range(t):\n \n l = q.qsize()\n for i in range(l):\n temp = q.get()\n\n # Count no.of non-visited nodes\n count = 0\n for ele in d[temp[0]]:\n if visit[ele] == 0: count += 1\n \n if temp[0] == target and count == 0: \n # If the target is reached and if its the end node\n return temp[1]\n \n if visit[temp[0]] != 0: # if already visited\n continue\n \n visit[temp[0]] = 1\n\n for ele in d[temp[0]]:\n if visit[ele] == 0: q.put([ele , temp[1]*(1/count)])\n \n \n l = q.qsize()\n for i in range(l):\n temp = q.get()\n if temp[0] == target:\n return temp[1]\n\n return 0\n``` | 2 | Given a binary array `nums`, you should delete one element from it.
Return _the size of the longest non-empty subarray containing only_ `1`_'s in the resulting array_. Return `0` if there is no such subarray.
**Example 1:**
**Input:** nums = \[1,1,0,1\]
**Output:** 3
**Explanation:** After deleting the number in position 2, \[1,1,1\] contains 3 numbers with value of 1's.
**Example 2:**
**Input:** nums = \[0,1,1,1,0,1,1,0,1\]
**Output:** 5
**Explanation:** After deleting the number in position 4, \[0,1,1,1,1,1,0,1\] longest subarray with value of 1's is \[1,1,1,1,1\].
**Example 3:**
**Input:** nums = \[1,1,1\]
**Output:** 2
**Explanation:** You must delete one element.
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`. | Use a variation of DFS with parameters 'curent_vertex' and 'current_time'. Update the probability considering to jump to one of the children vertices. |
[Python] Easy DFS/BFS with explanation | frog-position-after-t-seconds | 0 | 1 | **Idea**\nFirst we build an adjacency list using `edges`.\nWe then DFS through all the nodes. Do note that we can only visited a node once in an undirected graph. There are basically 2 solutions.\n1. Construct a undirected graph and transform it into a directed tree first **(method 1)**\n2. Use set to record all the visited nodes along the way **(method 2)**\n\n**Complexity**\nTime: `O(N)`\nSpace: `O(N)`\n\n**Python 3, DFS with recursion, method 2**\n```\nclass Solution:\n def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:\n nei = collections.defaultdict(set)\n for a, b in edges:\n nei[a].add(b)\n nei[b].add(a)\n \n visited, res = set(), 0.\n def dfs(leaf_id, p, time):\n nonlocal res\n if time >= t:\n if leaf_id == target: res = p\n return\n visited.add(leaf_id)\n neighbors = nei[leaf_id] - visited\n for n in neighbors or [leaf_id]:\n dfs(n, p / (len(neighbors) or 1), time + 1)\n dfs(1, 1, 0)\n return res\n```\n\n**Python 3, BFS without recursion, method 2**\n```\nclass Solution:\n def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:\n nei = collections.defaultdict(set)\n for a, b in edges:\n nei[a].add(b)\n nei[b].add(a)\n \n dp = collections.deque([(1, 1, 0)]) # state: leaf_id, possibility, timestamp\n visited = set()\n \n while dp:\n leaf, p, curr = dp.popleft()\n visited.add(leaf)\n \n if curr >= t:\n if leaf == target: return p\n continue\n \n neighbors = nei[leaf] - visited\n for n in neighbors or [leaf]:\n dp += (n, p / (len(neighbors) or 1), curr + 1),\n return 0.\n```\n\n**Python 3, DFS without recursion, method 2**\n```\nclass Solution:\n def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:\n nei = collections.defaultdict(set)\n for a, b in edges:\n nei[a].add(b)\n nei[b].add(a)\n \n dp = [(1, 1, 0)] # state: leaf_id, possibility, timestamp\n visited = set()\n \n while dp:\n leaf, p, curr = dp.pop()\n visited.add(leaf)\n \n if curr >= t:\n if leaf == target: return p\n continue\n \n neighbors = nei[leaf] - visited\n for n in neighbors or [leaf]:\n dp += (n, p / (len(neighbors) or 1), curr + 1),\n return 0.\n```\n\n**Python 3, DFS on tree without recursion, method 1**\n```\nclass Solution:\n def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:\n nei = collections.defaultdict(set)\n for a, b in edges:\n nei[a].add(b)\n nei[b].add(a)\n \n dp = collections.deque([1])\n while dp:\n leaf = dp.popleft()\n for n_ in nei[leaf]:\n nei[n_].remove(leaf)\n dp += n_,\n \n dp = [(1, 1, 0)]\n while dp:\n leaf, p, curr = dp.pop()\n if curr >= t:\n if leaf == target: return p\n continue\n for n in nei[leaf] or [leaf]:\n dp += (n, p / (len(nei[leaf]) or 1), curr+1),\n return 0.0\n```\n | 21 | Given an undirected tree consisting of `n` vertices numbered from `1` to `n`. A frog starts jumping from **vertex 1**. In one second, the frog jumps from its current vertex to another **unvisited** vertex if they are directly connected. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices, it jumps randomly to one of them with the same probability. Otherwise, when the frog can not jump to any unvisited vertex, it jumps forever on the same vertex.
The edges of the undirected tree are given in the array `edges`, where `edges[i] = [ai, bi]` means that exists an edge connecting the vertices `ai` and `bi`.
_Return the probability that after `t` seconds the frog is on the vertex `target`._ Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** n = 7, edges = \[\[1,2\],\[1,3\],\[1,7\],\[2,4\],\[2,6\],\[3,5\]\], t = 2, target = 4
**Output:** 0.16666666666666666
**Explanation:** The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 probability to the vertex 2 after **second 1** and then jumping with 1/2 probability to vertex 4 after **second 2**. Thus the probability for the frog is on the vertex 4 after 2 seconds is 1/3 \* 1/2 = 1/6 = 0.16666666666666666.
**Example 2:**
**Input:** n = 7, edges = \[\[1,2\],\[1,3\],\[1,7\],\[2,4\],\[2,6\],\[3,5\]\], t = 1, target = 7
**Output:** 0.3333333333333333
**Explanation:** The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 = 0.3333333333333333 probability to the vertex 7 after **second 1**.
**Constraints:**
* `1 <= n <= 100`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `1 <= ai, bi <= n`
* `1 <= t <= 50`
* `1 <= target <= n` | null |
[Python] Easy DFS/BFS with explanation | frog-position-after-t-seconds | 0 | 1 | **Idea**\nFirst we build an adjacency list using `edges`.\nWe then DFS through all the nodes. Do note that we can only visited a node once in an undirected graph. There are basically 2 solutions.\n1. Construct a undirected graph and transform it into a directed tree first **(method 1)**\n2. Use set to record all the visited nodes along the way **(method 2)**\n\n**Complexity**\nTime: `O(N)`\nSpace: `O(N)`\n\n**Python 3, DFS with recursion, method 2**\n```\nclass Solution:\n def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:\n nei = collections.defaultdict(set)\n for a, b in edges:\n nei[a].add(b)\n nei[b].add(a)\n \n visited, res = set(), 0.\n def dfs(leaf_id, p, time):\n nonlocal res\n if time >= t:\n if leaf_id == target: res = p\n return\n visited.add(leaf_id)\n neighbors = nei[leaf_id] - visited\n for n in neighbors or [leaf_id]:\n dfs(n, p / (len(neighbors) or 1), time + 1)\n dfs(1, 1, 0)\n return res\n```\n\n**Python 3, BFS without recursion, method 2**\n```\nclass Solution:\n def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:\n nei = collections.defaultdict(set)\n for a, b in edges:\n nei[a].add(b)\n nei[b].add(a)\n \n dp = collections.deque([(1, 1, 0)]) # state: leaf_id, possibility, timestamp\n visited = set()\n \n while dp:\n leaf, p, curr = dp.popleft()\n visited.add(leaf)\n \n if curr >= t:\n if leaf == target: return p\n continue\n \n neighbors = nei[leaf] - visited\n for n in neighbors or [leaf]:\n dp += (n, p / (len(neighbors) or 1), curr + 1),\n return 0.\n```\n\n**Python 3, DFS without recursion, method 2**\n```\nclass Solution:\n def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:\n nei = collections.defaultdict(set)\n for a, b in edges:\n nei[a].add(b)\n nei[b].add(a)\n \n dp = [(1, 1, 0)] # state: leaf_id, possibility, timestamp\n visited = set()\n \n while dp:\n leaf, p, curr = dp.pop()\n visited.add(leaf)\n \n if curr >= t:\n if leaf == target: return p\n continue\n \n neighbors = nei[leaf] - visited\n for n in neighbors or [leaf]:\n dp += (n, p / (len(neighbors) or 1), curr + 1),\n return 0.\n```\n\n**Python 3, DFS on tree without recursion, method 1**\n```\nclass Solution:\n def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:\n nei = collections.defaultdict(set)\n for a, b in edges:\n nei[a].add(b)\n nei[b].add(a)\n \n dp = collections.deque([1])\n while dp:\n leaf = dp.popleft()\n for n_ in nei[leaf]:\n nei[n_].remove(leaf)\n dp += n_,\n \n dp = [(1, 1, 0)]\n while dp:\n leaf, p, curr = dp.pop()\n if curr >= t:\n if leaf == target: return p\n continue\n for n in nei[leaf] or [leaf]:\n dp += (n, p / (len(nei[leaf]) or 1), curr+1),\n return 0.0\n```\n | 21 | Given a binary array `nums`, you should delete one element from it.
Return _the size of the longest non-empty subarray containing only_ `1`_'s in the resulting array_. Return `0` if there is no such subarray.
**Example 1:**
**Input:** nums = \[1,1,0,1\]
**Output:** 3
**Explanation:** After deleting the number in position 2, \[1,1,1\] contains 3 numbers with value of 1's.
**Example 2:**
**Input:** nums = \[0,1,1,1,0,1,1,0,1\]
**Output:** 5
**Explanation:** After deleting the number in position 4, \[0,1,1,1,1,1,0,1\] longest subarray with value of 1's is \[1,1,1,1,1\].
**Example 3:**
**Input:** nums = \[1,1,1\]
**Output:** 2
**Explanation:** You must delete one element.
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`. | Use a variation of DFS with parameters 'curent_vertex' and 'current_time'. Update the probability considering to jump to one of the children vertices. |
BFS Based Appraoch that beats 95% of all the entries || Pyhton 3 Solution | frog-position-after-t-seconds | 0 | 1 | # Intuition\nLooking at the question the first thing that strikes is a level order traversal of the graph and based on this the answer will be calculated\n# Approach\nDoing a Normal BFS wont work here\n\nOne of the most important lines is this questions is that whenever our frog reachs to target node and if there is more time buffer left then along with this node being a leaf then we can stay at the same place till the time elapses\n\nAlso is this is not the case then we go ahead with the normal BFS related works\n# Complexity\n- Time complexity:\nHere The Time Complexity is O(N) as each node is being visited only once\n\n- Space complexity:\nSpace Complexity is also O(2*N) as only a visitedArray and a queue is being used\n# Code\n```\nclass Solution:\n def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:\n \n\n graphDict = {}\n for i in range(1,n+1):\n graphDict[i] = []\n\n for ele in edges:\n graphDict[ele[0]].append(ele[1])\n graphDict[ele[1]].append(ele[0])\n\n queueArray = []\n queueArray.append([1,1,0])\n visitedArray = [False for i in range(n+1)]\n\n while queueArray:\n\n topNode = queueArray.pop(0)\n topNodeValue , topNodeProb , time = topNode\n visitedArray[topNodeValue] = True\n\n if topNodeValue==target and time==t:\n return topNodeProb\n if topNodeValue==target and time<=t:\n totalChildren = 0\n for adjNode in graphDict[topNodeValue]:\n if visitedArray[adjNode] is False:\n totalChildren+=1\n if totalChildren==0:\n return topNodeProb\n\n totalChildren = 0\n for adjNode in graphDict[topNodeValue]:\n if visitedArray[adjNode] is False:\n totalChildren+=1\n if totalChildren==0:\n newProb = 0\n else:\n newProb = topNodeProb/totalChildren\n\n for adjNode in graphDict[topNodeValue]:\n if visitedArray[adjNode] is False:\n queueArray.append([adjNode,newProb,time+1])\n\n return 0\n\n\n``` | 0 | Given an undirected tree consisting of `n` vertices numbered from `1` to `n`. A frog starts jumping from **vertex 1**. In one second, the frog jumps from its current vertex to another **unvisited** vertex if they are directly connected. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices, it jumps randomly to one of them with the same probability. Otherwise, when the frog can not jump to any unvisited vertex, it jumps forever on the same vertex.
The edges of the undirected tree are given in the array `edges`, where `edges[i] = [ai, bi]` means that exists an edge connecting the vertices `ai` and `bi`.
_Return the probability that after `t` seconds the frog is on the vertex `target`._ Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** n = 7, edges = \[\[1,2\],\[1,3\],\[1,7\],\[2,4\],\[2,6\],\[3,5\]\], t = 2, target = 4
**Output:** 0.16666666666666666
**Explanation:** The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 probability to the vertex 2 after **second 1** and then jumping with 1/2 probability to vertex 4 after **second 2**. Thus the probability for the frog is on the vertex 4 after 2 seconds is 1/3 \* 1/2 = 1/6 = 0.16666666666666666.
**Example 2:**
**Input:** n = 7, edges = \[\[1,2\],\[1,3\],\[1,7\],\[2,4\],\[2,6\],\[3,5\]\], t = 1, target = 7
**Output:** 0.3333333333333333
**Explanation:** The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 = 0.3333333333333333 probability to the vertex 7 after **second 1**.
**Constraints:**
* `1 <= n <= 100`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `1 <= ai, bi <= n`
* `1 <= t <= 50`
* `1 <= target <= n` | null |
BFS Based Appraoch that beats 95% of all the entries || Pyhton 3 Solution | frog-position-after-t-seconds | 0 | 1 | # Intuition\nLooking at the question the first thing that strikes is a level order traversal of the graph and based on this the answer will be calculated\n# Approach\nDoing a Normal BFS wont work here\n\nOne of the most important lines is this questions is that whenever our frog reachs to target node and if there is more time buffer left then along with this node being a leaf then we can stay at the same place till the time elapses\n\nAlso is this is not the case then we go ahead with the normal BFS related works\n# Complexity\n- Time complexity:\nHere The Time Complexity is O(N) as each node is being visited only once\n\n- Space complexity:\nSpace Complexity is also O(2*N) as only a visitedArray and a queue is being used\n# Code\n```\nclass Solution:\n def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:\n \n\n graphDict = {}\n for i in range(1,n+1):\n graphDict[i] = []\n\n for ele in edges:\n graphDict[ele[0]].append(ele[1])\n graphDict[ele[1]].append(ele[0])\n\n queueArray = []\n queueArray.append([1,1,0])\n visitedArray = [False for i in range(n+1)]\n\n while queueArray:\n\n topNode = queueArray.pop(0)\n topNodeValue , topNodeProb , time = topNode\n visitedArray[topNodeValue] = True\n\n if topNodeValue==target and time==t:\n return topNodeProb\n if topNodeValue==target and time<=t:\n totalChildren = 0\n for adjNode in graphDict[topNodeValue]:\n if visitedArray[adjNode] is False:\n totalChildren+=1\n if totalChildren==0:\n return topNodeProb\n\n totalChildren = 0\n for adjNode in graphDict[topNodeValue]:\n if visitedArray[adjNode] is False:\n totalChildren+=1\n if totalChildren==0:\n newProb = 0\n else:\n newProb = topNodeProb/totalChildren\n\n for adjNode in graphDict[topNodeValue]:\n if visitedArray[adjNode] is False:\n queueArray.append([adjNode,newProb,time+1])\n\n return 0\n\n\n``` | 0 | Given a binary array `nums`, you should delete one element from it.
Return _the size of the longest non-empty subarray containing only_ `1`_'s in the resulting array_. Return `0` if there is no such subarray.
**Example 1:**
**Input:** nums = \[1,1,0,1\]
**Output:** 3
**Explanation:** After deleting the number in position 2, \[1,1,1\] contains 3 numbers with value of 1's.
**Example 2:**
**Input:** nums = \[0,1,1,1,0,1,1,0,1\]
**Output:** 5
**Explanation:** After deleting the number in position 4, \[0,1,1,1,1,1,0,1\] longest subarray with value of 1's is \[1,1,1,1,1\].
**Example 3:**
**Input:** nums = \[1,1,1\]
**Output:** 2
**Explanation:** You must delete one element.
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`. | Use a variation of DFS with parameters 'curent_vertex' and 'current_time'. Update the probability considering to jump to one of the children vertices. |
🔥 Pandas Simple 1 Line Solution For Beginners 💯 | replace-employee-id-with-the-unique-identifier | 0 | 1 | **\uD83D\uDD3C IF YOU FIND THIS POST HELPFUL PLEASE UPVOTE \uD83D\uDC4D**\n```\nimport pandas as pd\n\ndef replace_employee_id(employees: pd.DataFrame, employee_uni: pd.DataFrame) -> pd.DataFrame:\n \n result = pd.merge(employees, employee_uni, on=\'id\', how=\'left\')\n \n return result[[\'unique_id\', \'name\']]\n```\n**Thank you for reading! \uD83D\uDE04 Comment if you have any questions or feedback.** | 3 | You are given an integer array `nums`.
In one move, you can choose one element of `nums` and change it to **any value**.
Return _the minimum difference between the largest and smallest value of `nums` **after performing at most three moves**_.
**Example 1:**
**Input:** nums = \[5,3,2,4\]
**Output:** 0
**Explanation:** We can make at most 3 moves.
In the first move, change 2 to 3. nums becomes \[5,3,3,4\].
In the second move, change 4 to 3. nums becomes \[5,3,3,3\].
In the third move, change 5 to 3. nums becomes \[3,3,3,3\].
After performing 3 moves, the difference between the minimum and maximum is 3 - 3 = 0.
**Example 2:**
**Input:** nums = \[1,5,0,10,14\]
**Output:** 1
**Explanation:** We can make at most 3 moves.
In the first move, change 5 to 0. nums becomes \[1,0,0,10,14\].
In the second move, change 10 to 0. nums becomes \[1,0,0,0,14\].
In the third move, change 14 to 1. nums becomes \[1,0,0,0,1\].
After performing 3 moves, the difference between the minimum and maximum is 1 - 0 = 0.
It can be shown that there is no way to make the difference 0 in 3 moves.
**Example 3:**
**Input:** nums = \[3,100,20\]
**Output:** 0
**Explanation:** We can make at most 3 moves.
In the first move, change 100 to 7. nums becomes \[4,7,20\].
In the second move, change 20 to 7. nums becomes \[4,7,7\].
In the third move, change 4 to 3. nums becomes \[7,7,7\].
After performing 3 moves, the difference between the minimum and maximum is 7 - 7 = 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
Pandas vs SQL | Elegant & Short | All 30 Days of Pandas solutions ✅ | replace-employee-id-with-the-unique-identifier | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```Python []\ndef replace_employee_id(employees: pd.DataFrame, employee_uni: pd.DataFrame) -> pd.DataFrame:\n return pd.merge(\n employees, employee_uni, how=\'left\', on=\'id\'\n )[[\'unique_id\', \'name\']]\n```\n```SQL []\nSELECT eu.unique_id,\n e.name\n FROM Employees e\n LEFT JOIN EmployeeUNI eu\n ON e.id = eu.id;\n```\n\n# Important!\n###### If you like the solution or find it useful, feel free to **upvote** for it, it will support me in creating high quality solutions)\n\n# 30 Days of Pandas solutions\n\n### Data Filtering \u2705\n- [Big Countries](https://leetcode.com/problems/big-countries/solutions/3848474/pandas-elegant-short-1-line/)\n- [Recyclable and Low Fat Products](https://leetcode.com/problems/recyclable-and-low-fat-products/solutions/3848500/pandas-elegant-short-1-line/)\n- [Customers Who Never Order](https://leetcode.com/problems/customers-who-never-order/solutions/3848527/pandas-elegant-short-1-line/)\n- [Article Views I](https://leetcode.com/problems/article-views-i/solutions/3867192/pandas-elegant-short-1-line/)\n\n\n### String Methods \u2705\n- [Invalid Tweets](https://leetcode.com/problems/invalid-tweets/solutions/3849121/pandas-elegant-short-1-line/)\n- [Calculate Special Bonus](https://leetcode.com/problems/calculate-special-bonus/solutions/3867209/pandas-elegant-short-1-line/)\n- [Fix Names in a Table](https://leetcode.com/problems/fix-names-in-a-table/solutions/3849167/pandas-elegant-short-1-line/)\n- [Find Users With Valid E-Mails](https://leetcode.com/problems/find-users-with-valid-e-mails/solutions/3849177/pandas-elegant-short-1-line/)\n- [Patients With a Condition](https://leetcode.com/problems/patients-with-a-condition/solutions/3849196/pandas-elegant-short-1-line-regex/)\n\n\n### Data Manipulation \u2705\n- [Nth Highest Salary](https://leetcode.com/problems/nth-highest-salary/solutions/3867257/pandas-elegant-short-1-line/)\n- [Second Highest Salary](https://leetcode.com/problems/second-highest-salary/solutions/3867278/pandas-elegant-short/)\n- [Department Highest Salary](https://leetcode.com/problems/department-highest-salary/solutions/3867312/pandas-elegant-short-1-line/)\n- [Rank Scores](https://leetcode.com/problems/rank-scores/solutions/3872817/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Delete Duplicate Emails](https://leetcode.com/problems/delete-duplicate-emails/solutions/3849211/pandas-elegant-short/)\n- [Rearrange Products Table](https://leetcode.com/problems/rearrange-products-table/solutions/3849226/pandas-elegant-short-1-line/)\n\n\n### Statistics \u2705\n- [The Number of Rich Customers](https://leetcode.com/problems/the-number-of-rich-customers/solutions/3849251/pandas-elegant-short-1-line/)\n- [Immediate Food Delivery I](https://leetcode.com/problems/immediate-food-delivery-i/solutions/3872719/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Count Salary Categories](https://leetcode.com/problems/count-salary-categories/solutions/3872801/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n\n### Data Aggregation \u2705\n- [Find Total Time Spent by Each Employee](https://leetcode.com/problems/find-total-time-spent-by-each-employee/solutions/3872715/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Game Play Analysis I](https://leetcode.com/problems/game-play-analysis-i/solutions/3863223/pandas-elegant-short-1-line/)\n- [Number of Unique Subjects Taught by Each Teacher](https://leetcode.com/problems/number-of-unique-subjects-taught-by-each-teacher/solutions/3863239/pandas-elegant-short-1-line/)\n- [Classes More Than 5 Students](https://leetcode.com/problems/classes-more-than-5-students/solutions/3863249/pandas-elegant-short/)\n- [Customer Placing the Largest Number of Orders](https://leetcode.com/problems/customer-placing-the-largest-number-of-orders/solutions/3863257/pandas-elegant-short-1-line/)\n- [Group Sold Products By The Date](https://leetcode.com/problems/group-sold-products-by-the-date/solutions/3863267/pandas-elegant-short-1-line/)\n- [Daily Leads and Partners](https://leetcode.com/problems/daily-leads-and-partners/solutions/3863279/pandas-elegant-short-1-line/)\n\n\n### Data Aggregation \u2705\n- [Actors and Directors Who Cooperated At Least Three Times](https://leetcode.com/problems/actors-and-directors-who-cooperated-at-least-three-times/solutions/3863309/pandas-elegant-short/)\n- [Replace Employee ID With The Unique Identifier](https://leetcode.com/problems/replace-employee-id-with-the-unique-identifier/solutions/3872822/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Students and Examinations](https://leetcode.com/problems/students-and-examinations/solutions/3872699/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Managers with at Least 5 Direct Reports](https://leetcode.com/problems/managers-with-at-least-5-direct-reports/solutions/3872861/pandas-elegant-short/)\n- [Sales Person](https://leetcode.com/problems/sales-person/solutions/3872712/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n | 14 | You are given an integer array `nums`.
In one move, you can choose one element of `nums` and change it to **any value**.
Return _the minimum difference between the largest and smallest value of `nums` **after performing at most three moves**_.
**Example 1:**
**Input:** nums = \[5,3,2,4\]
**Output:** 0
**Explanation:** We can make at most 3 moves.
In the first move, change 2 to 3. nums becomes \[5,3,3,4\].
In the second move, change 4 to 3. nums becomes \[5,3,3,3\].
In the third move, change 5 to 3. nums becomes \[3,3,3,3\].
After performing 3 moves, the difference between the minimum and maximum is 3 - 3 = 0.
**Example 2:**
**Input:** nums = \[1,5,0,10,14\]
**Output:** 1
**Explanation:** We can make at most 3 moves.
In the first move, change 5 to 0. nums becomes \[1,0,0,10,14\].
In the second move, change 10 to 0. nums becomes \[1,0,0,0,14\].
In the third move, change 14 to 1. nums becomes \[1,0,0,0,1\].
After performing 3 moves, the difference between the minimum and maximum is 1 - 0 = 0.
It can be shown that there is no way to make the difference 0 in 3 moves.
**Example 3:**
**Input:** nums = \[3,100,20\]
**Output:** 0
**Explanation:** We can make at most 3 moves.
In the first move, change 100 to 7. nums becomes \[4,7,20\].
In the second move, change 20 to 7. nums becomes \[4,7,7\].
In the third move, change 4 to 3. nums becomes \[7,7,7\].
After performing 3 moves, the difference between the minimum and maximum is 7 - 7 = 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109` | null |
Python3 Iterative and recursive DFS | find-a-corresponding-node-of-a-binary-tree-in-a-clone-of-that-tree | 0 | 1 | \n\n# Complexity\n- Time complexity: O(n), whenre n is the number of nodes in cloned tree\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(h), where h is the height of the cloned tree\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def getTargetCopy(self, original: TreeNode, cloned: TreeNode, target: TreeNode) -> TreeNode:\n #DFS\n stack = [(cloned)]\n while stack:\n n = stack.pop()\n if n.val == target.val: return n\n if n.left: stack.append(n.left)\n if n.right: stack.append(n.right)\n #Recursive DFS\n if not original: return None\n if original is target: return cloned\n return self.getTargetCopy(original.left, cloned.left, target) or self.getTargetCopy(original.right, cloned.right, target)\n\n``` | 1 | Given two binary trees `original` and `cloned` and given a reference to a node `target` in the original tree.
The `cloned` tree is a **copy of** the `original` tree.
Return _a reference to the same node_ in the `cloned` tree.
**Note** that you are **not allowed** to change any of the two trees or the `target` node and the answer **must be** a reference to a node in the `cloned` tree.
**Example 1:**
**Input:** tree = \[7,4,3,null,null,6,19\], target = 3
**Output:** 3
**Explanation:** In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
**Example 2:**
**Input:** tree = \[7\], target = 7
**Output:** 7
**Example 3:**
**Input:** tree = \[8,null,6,null,5,null,4,null,3,null,2,null,1\], target = 4
**Output:** 4
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 104]`.
* The values of the nodes of the `tree` are unique.
* `target` node is a node from the `original` tree and is not `null`.
**Follow up:** Could you solve the problem if repeated values on the tree are allowed? | You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row. Fill 0 and 2 first, then fill 1 in the upper row or lower row in turn but be careful about exhausting permitted 1s in each row. |
Python3 Iterative and recursive DFS | find-a-corresponding-node-of-a-binary-tree-in-a-clone-of-that-tree | 0 | 1 | \n\n# Complexity\n- Time complexity: O(n), whenre n is the number of nodes in cloned tree\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(h), where h is the height of the cloned tree\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def getTargetCopy(self, original: TreeNode, cloned: TreeNode, target: TreeNode) -> TreeNode:\n #DFS\n stack = [(cloned)]\n while stack:\n n = stack.pop()\n if n.val == target.val: return n\n if n.left: stack.append(n.left)\n if n.right: stack.append(n.right)\n #Recursive DFS\n if not original: return None\n if original is target: return cloned\n return self.getTargetCopy(original.left, cloned.left, target) or self.getTargetCopy(original.right, cloned.right, target)\n\n``` | 1 | You are given an array of integers `nums` and an integer `target`.
Return _the number of **non-empty** subsequences of_ `nums` _such that the sum of the minimum and maximum element on it is less or equal to_ `target`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[3,5,6,7\], target = 9
**Output:** 4
**Explanation:** There are 4 subsequences that satisfy the condition.
\[3\] -> Min value + max value <= target (3 + 3 <= 9)
\[3,5\] -> (3 + 5 <= 9)
\[3,5,6\] -> (3 + 6 <= 9)
\[3,6\] -> (3 + 6 <= 9)
**Example 2:**
**Input:** nums = \[3,3,6,8\], target = 10
**Output:** 6
**Explanation:** There are 6 subsequences that satisfy the condition. (nums can have repeated numbers).
\[3\] , \[3\] , \[3,3\], \[3,6\] , \[3,6\] , \[3,3,6\]
**Example 3:**
**Input:** nums = \[2,3,3,4,6,7\], target = 12
**Output:** 61
**Explanation:** There are 63 non-empty subsequences, two of them do not satisfy the condition (\[6,7\], \[7\]).
Number of valid subsequences (63 - 2 = 61).
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 106`
* `1 <= target <= 106` | null |
Easy to Understand || Beginner Friendly || Python 3 || Beats 100% Easy | find-a-corresponding-node-of-a-binary-tree-in-a-clone-of-that-tree | 0 | 1 | # Intuition\nThe problem asks us to find a corresponding node in a clone of a binary tree when given the original tree and a target node in the original tree. To solve this, we can perform a depth-first search (DFS) traversal of both trees to find the corresponding node in the cloned tree.\n\n# Approach\nWe use a recursive approach to traverse both the original and cloned trees simultaneously. At each step, we compare the values of the current nodes in both trees. If the value of the current node in the original tree matches the target value, we return the corresponding node from the cloned tree. If not, we recursively search in the left and right subtrees of both trees.\n\nWhen we find the target node in the original tree, we stop searching in the subtrees, improving the efficiency of the search. The code uses early returns to minimize recursive calls.\n\n# Complexity\n- Time complexity: `O(N)` \n - The time complexity of the code is `O(N)` where `N` is the number of nodes in the tree. In the worst case, we may need to visit all nodes in both trees during the depth-first search (DFS) traversal.\n \n- Space complexity: `O(H)` \n - The space complexity is `O(H)` where `H` is the height of the tree. This represents the maximum depth of the recursion stack during the DFS traversal. The space required for the recursion stack is determined by the height of the tree.\n\n\n```python\nclass Solution:\n def getTargetCopy(self, original: TreeNode, cloned: TreeNode, target: TreeNode) -> TreeNode:\n # If either the original or cloned node is None, return None\n if original is None or cloned is None:\n return None\n\n # Check if the current node\'s value in the original tree matches the target value\n if original.val == target.val:\n # If it matches, return the current node from the cloned tree\n return cloned\n\n # Recursively search in the left subtrees of both trees\n left = self.getTargetCopy(original.left, cloned.left, target)\n # If a match is found in the left subtree, return it\n if left is not None:\n return left\n\n # Recursively search in the right subtrees of both trees\n right = self.getTargetCopy(original.right, cloned.right, target)\n # Return the result of the search in the right subtree\n return right\n | 2 | Given two binary trees `original` and `cloned` and given a reference to a node `target` in the original tree.
The `cloned` tree is a **copy of** the `original` tree.
Return _a reference to the same node_ in the `cloned` tree.
**Note** that you are **not allowed** to change any of the two trees or the `target` node and the answer **must be** a reference to a node in the `cloned` tree.
**Example 1:**
**Input:** tree = \[7,4,3,null,null,6,19\], target = 3
**Output:** 3
**Explanation:** In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
**Example 2:**
**Input:** tree = \[7\], target = 7
**Output:** 7
**Example 3:**
**Input:** tree = \[8,null,6,null,5,null,4,null,3,null,2,null,1\], target = 4
**Output:** 4
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 104]`.
* The values of the nodes of the `tree` are unique.
* `target` node is a node from the `original` tree and is not `null`.
**Follow up:** Could you solve the problem if repeated values on the tree are allowed? | You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row. Fill 0 and 2 first, then fill 1 in the upper row or lower row in turn but be careful about exhausting permitted 1s in each row. |
Easy to Understand || Beginner Friendly || Python 3 || Beats 100% Easy | find-a-corresponding-node-of-a-binary-tree-in-a-clone-of-that-tree | 0 | 1 | # Intuition\nThe problem asks us to find a corresponding node in a clone of a binary tree when given the original tree and a target node in the original tree. To solve this, we can perform a depth-first search (DFS) traversal of both trees to find the corresponding node in the cloned tree.\n\n# Approach\nWe use a recursive approach to traverse both the original and cloned trees simultaneously. At each step, we compare the values of the current nodes in both trees. If the value of the current node in the original tree matches the target value, we return the corresponding node from the cloned tree. If not, we recursively search in the left and right subtrees of both trees.\n\nWhen we find the target node in the original tree, we stop searching in the subtrees, improving the efficiency of the search. The code uses early returns to minimize recursive calls.\n\n# Complexity\n- Time complexity: `O(N)` \n - The time complexity of the code is `O(N)` where `N` is the number of nodes in the tree. In the worst case, we may need to visit all nodes in both trees during the depth-first search (DFS) traversal.\n \n- Space complexity: `O(H)` \n - The space complexity is `O(H)` where `H` is the height of the tree. This represents the maximum depth of the recursion stack during the DFS traversal. The space required for the recursion stack is determined by the height of the tree.\n\n\n```python\nclass Solution:\n def getTargetCopy(self, original: TreeNode, cloned: TreeNode, target: TreeNode) -> TreeNode:\n # If either the original or cloned node is None, return None\n if original is None or cloned is None:\n return None\n\n # Check if the current node\'s value in the original tree matches the target value\n if original.val == target.val:\n # If it matches, return the current node from the cloned tree\n return cloned\n\n # Recursively search in the left subtrees of both trees\n left = self.getTargetCopy(original.left, cloned.left, target)\n # If a match is found in the left subtree, return it\n if left is not None:\n return left\n\n # Recursively search in the right subtrees of both trees\n right = self.getTargetCopy(original.right, cloned.right, target)\n # Return the result of the search in the right subtree\n return right\n | 2 | You are given an array of integers `nums` and an integer `target`.
Return _the number of **non-empty** subsequences of_ `nums` _such that the sum of the minimum and maximum element on it is less or equal to_ `target`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[3,5,6,7\], target = 9
**Output:** 4
**Explanation:** There are 4 subsequences that satisfy the condition.
\[3\] -> Min value + max value <= target (3 + 3 <= 9)
\[3,5\] -> (3 + 5 <= 9)
\[3,5,6\] -> (3 + 6 <= 9)
\[3,6\] -> (3 + 6 <= 9)
**Example 2:**
**Input:** nums = \[3,3,6,8\], target = 10
**Output:** 6
**Explanation:** There are 6 subsequences that satisfy the condition. (nums can have repeated numbers).
\[3\] , \[3\] , \[3,3\], \[3,6\] , \[3,6\] , \[3,3,6\]
**Example 3:**
**Input:** nums = \[2,3,3,4,6,7\], target = 12
**Output:** 61
**Explanation:** There are 63 non-empty subsequences, two of them do not satisfy the condition (\[6,7\], \[7\]).
Number of valid subsequences (63 - 2 = 61).
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 106`
* `1 <= target <= 106` | null |
Python Simple 2 approaches - Recursion(3 liner) and Morris | find-a-corresponding-node-of-a-binary-tree-in-a-clone-of-that-tree | 0 | 1 | I have implemented two approaches for this problem.\n1. #### Recursive Preorder \nThe recursive approach is easier to read and more concise (3 liner). The algorithm is quite straightforward as the second tree in which we need to find the `target` is cloned:\n1. Start a preoder traversal for both the trees simulataneously. \n2. If you hit the null nodes, return None\n3. If `target` matches the first tree\'s current node, return the current node from the cloned tree. Once a match is found, immediately return to the caller function.\n\n\n```\nclass Solution: \n def getTargetCopy(self, node1: TreeNode, node2: TreeNode, target: TreeNode) -> TreeNode: \n if not node1 or target == node1: # if node1 is null, node2 will also be null\n return node2\n \n return self.getTargetCopy(node1.left, node2.left, target) or self.getTargetCopy(node1.right, node2.right, target) \n```\n**Time - O(N)** - Iterate all nodes in tree atleast once\n**Space - O(N)** - space required for recursive call stack\n\n---\n\n2. #### Morris Traversal\n\nFor this approach, we need to understand the [Morris traversal](https://en.wikipedia.org/wiki/Tree_traversal#Morris_in-order_traversal_using_threading). This approach solves the problem with `O(1) ` space as it uses the concept of threading or connecting the inorder successor of the node. This modifies the tree temporarily for traversal. Due to this modification process, unlike recursive approach, we need to traverse the entire tree even if we have found the match. The whole tree traversal is required to restore the tree to its original state.\n\nBelow is my second implementation using Morris traversal. Though it looks ugly compared to Recursive approach, it does the job :)\n. \n```\nclass Solution: \n def getTargetCopy(self, original: TreeNode, cloned: TreeNode, target: TreeNode) -> TreeNode:\n \n curr1=original\n curr2=cloned\n \n found = None\n while curr1:\n if not curr1.left:\n if curr1==target:\n found=curr2\n curr1=curr1.right\n curr2=curr2.right\n else:\n temp1 = curr1.left\n temp2 = curr2.left\n \n while temp1.right and temp1.right!=curr1:\n temp1=temp1.right\n temp2=temp2.right\n \n if temp1.right==curr1:\n temp1.right=None\n temp2.right=None\n if curr1 == target:\n found=curr2\n curr1=curr1.right\n curr2=curr2.right\n else:\n temp1.right=curr1\n temp2.right=curr2\n curr1=curr1.left\n curr2=curr2.left\n return found\n```\n\n**Time - O(N)** - Iterate all nodes in tree atleast once\n**Space - O(1)** \n\n---\n\n***Please upvote if you find it useful***\n | 28 | Given two binary trees `original` and `cloned` and given a reference to a node `target` in the original tree.
The `cloned` tree is a **copy of** the `original` tree.
Return _a reference to the same node_ in the `cloned` tree.
**Note** that you are **not allowed** to change any of the two trees or the `target` node and the answer **must be** a reference to a node in the `cloned` tree.
**Example 1:**
**Input:** tree = \[7,4,3,null,null,6,19\], target = 3
**Output:** 3
**Explanation:** In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
**Example 2:**
**Input:** tree = \[7\], target = 7
**Output:** 7
**Example 3:**
**Input:** tree = \[8,null,6,null,5,null,4,null,3,null,2,null,1\], target = 4
**Output:** 4
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 104]`.
* The values of the nodes of the `tree` are unique.
* `target` node is a node from the `original` tree and is not `null`.
**Follow up:** Could you solve the problem if repeated values on the tree are allowed? | You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row. Fill 0 and 2 first, then fill 1 in the upper row or lower row in turn but be careful about exhausting permitted 1s in each row. |
Python Simple 2 approaches - Recursion(3 liner) and Morris | find-a-corresponding-node-of-a-binary-tree-in-a-clone-of-that-tree | 0 | 1 | I have implemented two approaches for this problem.\n1. #### Recursive Preorder \nThe recursive approach is easier to read and more concise (3 liner). The algorithm is quite straightforward as the second tree in which we need to find the `target` is cloned:\n1. Start a preoder traversal for both the trees simulataneously. \n2. If you hit the null nodes, return None\n3. If `target` matches the first tree\'s current node, return the current node from the cloned tree. Once a match is found, immediately return to the caller function.\n\n\n```\nclass Solution: \n def getTargetCopy(self, node1: TreeNode, node2: TreeNode, target: TreeNode) -> TreeNode: \n if not node1 or target == node1: # if node1 is null, node2 will also be null\n return node2\n \n return self.getTargetCopy(node1.left, node2.left, target) or self.getTargetCopy(node1.right, node2.right, target) \n```\n**Time - O(N)** - Iterate all nodes in tree atleast once\n**Space - O(N)** - space required for recursive call stack\n\n---\n\n2. #### Morris Traversal\n\nFor this approach, we need to understand the [Morris traversal](https://en.wikipedia.org/wiki/Tree_traversal#Morris_in-order_traversal_using_threading). This approach solves the problem with `O(1) ` space as it uses the concept of threading or connecting the inorder successor of the node. This modifies the tree temporarily for traversal. Due to this modification process, unlike recursive approach, we need to traverse the entire tree even if we have found the match. The whole tree traversal is required to restore the tree to its original state.\n\nBelow is my second implementation using Morris traversal. Though it looks ugly compared to Recursive approach, it does the job :)\n. \n```\nclass Solution: \n def getTargetCopy(self, original: TreeNode, cloned: TreeNode, target: TreeNode) -> TreeNode:\n \n curr1=original\n curr2=cloned\n \n found = None\n while curr1:\n if not curr1.left:\n if curr1==target:\n found=curr2\n curr1=curr1.right\n curr2=curr2.right\n else:\n temp1 = curr1.left\n temp2 = curr2.left\n \n while temp1.right and temp1.right!=curr1:\n temp1=temp1.right\n temp2=temp2.right\n \n if temp1.right==curr1:\n temp1.right=None\n temp2.right=None\n if curr1 == target:\n found=curr2\n curr1=curr1.right\n curr2=curr2.right\n else:\n temp1.right=curr1\n temp2.right=curr2\n curr1=curr1.left\n curr2=curr2.left\n return found\n```\n\n**Time - O(N)** - Iterate all nodes in tree atleast once\n**Space - O(1)** \n\n---\n\n***Please upvote if you find it useful***\n | 28 | You are given an array of integers `nums` and an integer `target`.
Return _the number of **non-empty** subsequences of_ `nums` _such that the sum of the minimum and maximum element on it is less or equal to_ `target`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[3,5,6,7\], target = 9
**Output:** 4
**Explanation:** There are 4 subsequences that satisfy the condition.
\[3\] -> Min value + max value <= target (3 + 3 <= 9)
\[3,5\] -> (3 + 5 <= 9)
\[3,5,6\] -> (3 + 6 <= 9)
\[3,6\] -> (3 + 6 <= 9)
**Example 2:**
**Input:** nums = \[3,3,6,8\], target = 10
**Output:** 6
**Explanation:** There are 6 subsequences that satisfy the condition. (nums can have repeated numbers).
\[3\] , \[3\] , \[3,3\], \[3,6\] , \[3,6\] , \[3,3,6\]
**Example 3:**
**Input:** nums = \[2,3,3,4,6,7\], target = 12
**Output:** 61
**Explanation:** There are 63 non-empty subsequences, two of them do not satisfy the condition (\[6,7\], \[7\]).
Number of valid subsequences (63 - 2 = 61).
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 106`
* `1 <= target <= 106` | null |
Python/JS/Java/C++ O(n) by DFS or BFS [w/ Hint] | find-a-corresponding-node-of-a-binary-tree-in-a-clone-of-that-tree | 1 | 1 | ---\n**Hint**:\n\nDescription says cloned tree is a full copy of original one.\nIn addtion, it also guarantees target node is selected from original tree.\n\nThat is, the **topology** for both cloned tree and original tree **is the same**.\n\nTherefore, we can develop a paired DFS or BFS traversal algorithm to locate the target by directly [checking identity with is operator](https://docs.python.org/3/reference/expressions.html#is-not) without comparing node.val.\n\n---\n\n**Implementation** by paired DFS\n\nPython:\n\n```\nclass Solution:\n def getTargetCopy(self, original: TreeNode, cloned: TreeNode, target: TreeNode) -> TreeNode:\n \n if not original:\n ## base case or stop condition:\n # empty node or empty tree\n return None\n \n ## general cases:\n if original is target:\n \n # current original node is target, so is cloned\n return cloned\n \n # either left subtree has target or right subtree has target\n return self.getTargetCopy(original.left, cloned.left, target) or self.getTargetCopy(original.right, cloned.right, target)\n```\n\n---\n\nJavascript:\n\n```\nvar getTargetCopy = function(original, cloned, target) {\n \n if( original == null ){\n \n // Base case aka stop condition\n // empty tree or empty node\n return null;\n }\n \n // General cases\n if( original == target ){\n \n // current original node is target, so is cloned\n return cloned;\n }\n \n // Either left subtree has target, or right subtree has target\n return getTargetCopy(original.left, cloned.left, target) || \n getTargetCopy(original.right, cloned.right, target);\n \n};\n```\n\n---\n\nJava:\n\n```\nclass Solution {\n public final TreeNode getTargetCopy(final TreeNode original, final TreeNode cloned, final TreeNode target) {\n\n if( original == null ){\n // Base case aka stop condition\n // empty tree or empty node\n return null;\n }\n \n // General case:\n if( original == target ){\n // current original node is target, so is cloned\n return cloned;\n }\n \n // Either left subtree has target, or right subtree has target\n TreeNode left = getTargetCopy(original.left, cloned.left, target);\n \n if( left != null ){ \n return left; \n \n }else{\n return getTargetCopy(original.right, cloned.right, target);\n } \n \n \n }\n}\n```\n\n---\n\nC++\n\n```\nclass Solution {\npublic:\n TreeNode* getTargetCopy(TreeNode* original, TreeNode* cloned, TreeNode* target) {\n \n if( original == NULL ){\n // Base case aka stop condition\n // empty tree or empty node\n return NULL;\n }\n \n // General case:\n if( original == target ){\n // current original node is target, so is cloned\n return cloned;\n }\n \n // Either left subtree has target, or right subtree has target\n TreeNode *left = getTargetCopy(original->left, cloned->left, target);\n \n if( left != NULL ){ \n return left; \n \n }else{\n return getTargetCopy(original->right, cloned->right, target);\n }\n \n }\n};\n```\n\n\n---\n\nShare another two implementation:\n\n**Implementation** by paired DFS:\n```\nclass Solution:\n def getTargetCopy(self, original: TreeNode, cloned: TreeNode, target: TreeNode) -> TreeNode:\n \n def helper( node: TreeNode, cloned: TreeNode):\n \n if node is target:\n yield cloned\n \n if node.left:\n yield from helper( node.left, cloned.left )\n \n if node.right:\n yield from helper( node.right, cloned.right )\n \n # -------------------------------------------------------------------\n return next( helper(original, cloned) )\n```\n\n---\n\n**Implementation** by paired BFS:\n```\nfrom collections import deque\nclass Solution:\n def getTargetCopy(self, original: TreeNode, cloned: TreeNode, target: TreeNode) -> TreeNode:\n \n def helper( node: TreeNode, mirror: TreeNode ):\n \n traversal_queue = deque([node])\n mirror_queue = deque([mirror])\n \n while traversal_queue:\n \n cur, clone = traversal_queue.pop(), mirror_queue.pop()\n \n if cur:\n \n if cur is target:\n yield clone\n \n traversal_queue.append( cur.left )\n traversal_queue.append( cur.right )\n \n mirror_queue.append( clone.left )\n mirror_queue.append( clone.right )\n \n # -------------------------------------------------------------------\n return next( helper(original, cloned ) ) \n```\n\n---\n\nReference:\n\n[1] [Python official docs about **is** and **is not** operator](https://docs.python.org/3/reference/expressions.html#is-not)\n\n[2] [Python official docs about generator and **yield** statement](https://docs.python.org/3/howto/functional.html#generators) | 41 | Given two binary trees `original` and `cloned` and given a reference to a node `target` in the original tree.
The `cloned` tree is a **copy of** the `original` tree.
Return _a reference to the same node_ in the `cloned` tree.
**Note** that you are **not allowed** to change any of the two trees or the `target` node and the answer **must be** a reference to a node in the `cloned` tree.
**Example 1:**
**Input:** tree = \[7,4,3,null,null,6,19\], target = 3
**Output:** 3
**Explanation:** In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
**Example 2:**
**Input:** tree = \[7\], target = 7
**Output:** 7
**Example 3:**
**Input:** tree = \[8,null,6,null,5,null,4,null,3,null,2,null,1\], target = 4
**Output:** 4
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 104]`.
* The values of the nodes of the `tree` are unique.
* `target` node is a node from the `original` tree and is not `null`.
**Follow up:** Could you solve the problem if repeated values on the tree are allowed? | You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row. Fill 0 and 2 first, then fill 1 in the upper row or lower row in turn but be careful about exhausting permitted 1s in each row. |
Python/JS/Java/C++ O(n) by DFS or BFS [w/ Hint] | find-a-corresponding-node-of-a-binary-tree-in-a-clone-of-that-tree | 1 | 1 | ---\n**Hint**:\n\nDescription says cloned tree is a full copy of original one.\nIn addtion, it also guarantees target node is selected from original tree.\n\nThat is, the **topology** for both cloned tree and original tree **is the same**.\n\nTherefore, we can develop a paired DFS or BFS traversal algorithm to locate the target by directly [checking identity with is operator](https://docs.python.org/3/reference/expressions.html#is-not) without comparing node.val.\n\n---\n\n**Implementation** by paired DFS\n\nPython:\n\n```\nclass Solution:\n def getTargetCopy(self, original: TreeNode, cloned: TreeNode, target: TreeNode) -> TreeNode:\n \n if not original:\n ## base case or stop condition:\n # empty node or empty tree\n return None\n \n ## general cases:\n if original is target:\n \n # current original node is target, so is cloned\n return cloned\n \n # either left subtree has target or right subtree has target\n return self.getTargetCopy(original.left, cloned.left, target) or self.getTargetCopy(original.right, cloned.right, target)\n```\n\n---\n\nJavascript:\n\n```\nvar getTargetCopy = function(original, cloned, target) {\n \n if( original == null ){\n \n // Base case aka stop condition\n // empty tree or empty node\n return null;\n }\n \n // General cases\n if( original == target ){\n \n // current original node is target, so is cloned\n return cloned;\n }\n \n // Either left subtree has target, or right subtree has target\n return getTargetCopy(original.left, cloned.left, target) || \n getTargetCopy(original.right, cloned.right, target);\n \n};\n```\n\n---\n\nJava:\n\n```\nclass Solution {\n public final TreeNode getTargetCopy(final TreeNode original, final TreeNode cloned, final TreeNode target) {\n\n if( original == null ){\n // Base case aka stop condition\n // empty tree or empty node\n return null;\n }\n \n // General case:\n if( original == target ){\n // current original node is target, so is cloned\n return cloned;\n }\n \n // Either left subtree has target, or right subtree has target\n TreeNode left = getTargetCopy(original.left, cloned.left, target);\n \n if( left != null ){ \n return left; \n \n }else{\n return getTargetCopy(original.right, cloned.right, target);\n } \n \n \n }\n}\n```\n\n---\n\nC++\n\n```\nclass Solution {\npublic:\n TreeNode* getTargetCopy(TreeNode* original, TreeNode* cloned, TreeNode* target) {\n \n if( original == NULL ){\n // Base case aka stop condition\n // empty tree or empty node\n return NULL;\n }\n \n // General case:\n if( original == target ){\n // current original node is target, so is cloned\n return cloned;\n }\n \n // Either left subtree has target, or right subtree has target\n TreeNode *left = getTargetCopy(original->left, cloned->left, target);\n \n if( left != NULL ){ \n return left; \n \n }else{\n return getTargetCopy(original->right, cloned->right, target);\n }\n \n }\n};\n```\n\n\n---\n\nShare another two implementation:\n\n**Implementation** by paired DFS:\n```\nclass Solution:\n def getTargetCopy(self, original: TreeNode, cloned: TreeNode, target: TreeNode) -> TreeNode:\n \n def helper( node: TreeNode, cloned: TreeNode):\n \n if node is target:\n yield cloned\n \n if node.left:\n yield from helper( node.left, cloned.left )\n \n if node.right:\n yield from helper( node.right, cloned.right )\n \n # -------------------------------------------------------------------\n return next( helper(original, cloned) )\n```\n\n---\n\n**Implementation** by paired BFS:\n```\nfrom collections import deque\nclass Solution:\n def getTargetCopy(self, original: TreeNode, cloned: TreeNode, target: TreeNode) -> TreeNode:\n \n def helper( node: TreeNode, mirror: TreeNode ):\n \n traversal_queue = deque([node])\n mirror_queue = deque([mirror])\n \n while traversal_queue:\n \n cur, clone = traversal_queue.pop(), mirror_queue.pop()\n \n if cur:\n \n if cur is target:\n yield clone\n \n traversal_queue.append( cur.left )\n traversal_queue.append( cur.right )\n \n mirror_queue.append( clone.left )\n mirror_queue.append( clone.right )\n \n # -------------------------------------------------------------------\n return next( helper(original, cloned ) ) \n```\n\n---\n\nReference:\n\n[1] [Python official docs about **is** and **is not** operator](https://docs.python.org/3/reference/expressions.html#is-not)\n\n[2] [Python official docs about generator and **yield** statement](https://docs.python.org/3/howto/functional.html#generators) | 41 | You are given an array of integers `nums` and an integer `target`.
Return _the number of **non-empty** subsequences of_ `nums` _such that the sum of the minimum and maximum element on it is less or equal to_ `target`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[3,5,6,7\], target = 9
**Output:** 4
**Explanation:** There are 4 subsequences that satisfy the condition.
\[3\] -> Min value + max value <= target (3 + 3 <= 9)
\[3,5\] -> (3 + 5 <= 9)
\[3,5,6\] -> (3 + 6 <= 9)
\[3,6\] -> (3 + 6 <= 9)
**Example 2:**
**Input:** nums = \[3,3,6,8\], target = 10
**Output:** 6
**Explanation:** There are 6 subsequences that satisfy the condition. (nums can have repeated numbers).
\[3\] , \[3\] , \[3,3\], \[3,6\] , \[3,6\] , \[3,3,6\]
**Example 3:**
**Input:** nums = \[2,3,3,4,6,7\], target = 12
**Output:** 61
**Explanation:** There are 63 non-empty subsequences, two of them do not satisfy the condition (\[6,7\], \[7\]).
Number of valid subsequences (63 - 2 = 61).
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 106`
* `1 <= target <= 106` | null |
Best Python Solution for Beginners | Simple Recursion | find-a-corresponding-node-of-a-binary-tree-in-a-clone-of-that-tree | 0 | 1 | \n# Code\n```\nclass Solution:\n def getTargetCopy(self, original: TreeNode, cloned: TreeNode, target: TreeNode) -> TreeNode:\n if not original:\n return original\n else:\n if original == target:\n return cloned\n else:\n left = self.getTargetCopy(original.left,cloned.left,target)\n if left :\n return left\n else:\n return self.getTargetCopy(original.right,cloned.right,target)\n``` | 1 | Given two binary trees `original` and `cloned` and given a reference to a node `target` in the original tree.
The `cloned` tree is a **copy of** the `original` tree.
Return _a reference to the same node_ in the `cloned` tree.
**Note** that you are **not allowed** to change any of the two trees or the `target` node and the answer **must be** a reference to a node in the `cloned` tree.
**Example 1:**
**Input:** tree = \[7,4,3,null,null,6,19\], target = 3
**Output:** 3
**Explanation:** In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
**Example 2:**
**Input:** tree = \[7\], target = 7
**Output:** 7
**Example 3:**
**Input:** tree = \[8,null,6,null,5,null,4,null,3,null,2,null,1\], target = 4
**Output:** 4
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 104]`.
* The values of the nodes of the `tree` are unique.
* `target` node is a node from the `original` tree and is not `null`.
**Follow up:** Could you solve the problem if repeated values on the tree are allowed? | You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row. Fill 0 and 2 first, then fill 1 in the upper row or lower row in turn but be careful about exhausting permitted 1s in each row. |
Best Python Solution for Beginners | Simple Recursion | find-a-corresponding-node-of-a-binary-tree-in-a-clone-of-that-tree | 0 | 1 | \n# Code\n```\nclass Solution:\n def getTargetCopy(self, original: TreeNode, cloned: TreeNode, target: TreeNode) -> TreeNode:\n if not original:\n return original\n else:\n if original == target:\n return cloned\n else:\n left = self.getTargetCopy(original.left,cloned.left,target)\n if left :\n return left\n else:\n return self.getTargetCopy(original.right,cloned.right,target)\n``` | 1 | You are given an array of integers `nums` and an integer `target`.
Return _the number of **non-empty** subsequences of_ `nums` _such that the sum of the minimum and maximum element on it is less or equal to_ `target`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[3,5,6,7\], target = 9
**Output:** 4
**Explanation:** There are 4 subsequences that satisfy the condition.
\[3\] -> Min value + max value <= target (3 + 3 <= 9)
\[3,5\] -> (3 + 5 <= 9)
\[3,5,6\] -> (3 + 6 <= 9)
\[3,6\] -> (3 + 6 <= 9)
**Example 2:**
**Input:** nums = \[3,3,6,8\], target = 10
**Output:** 6
**Explanation:** There are 6 subsequences that satisfy the condition. (nums can have repeated numbers).
\[3\] , \[3\] , \[3,3\], \[3,6\] , \[3,6\] , \[3,3,6\]
**Example 3:**
**Input:** nums = \[2,3,3,4,6,7\], target = 12
**Output:** 61
**Explanation:** There are 63 non-empty subsequences, two of them do not satisfy the condition (\[6,7\], \[7\]).
Number of valid subsequences (63 - 2 = 61).
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 106`
* `1 <= target <= 106` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.