title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python 1L / Rust 2-3 L / Go a lot. | sort-integers-by-the-number-of-1-bits | 0 | 1 | # Intuition\nAll you need is to count the number of ones, create tules of `(cnt, v)` and then do sorting. Many languages allow to do this in one line\n\n# Complexity\n- Time complexity: $O(n \\log n)$\n- Space complexity: $O(n)$\n\n# Code\n```Rust []\nimpl Solution {\n pub fn sort_by_bits(arr: Vec<i32>) -> Vec<i32> {\n let mut data: Vec<(u32, i32)> = arr.iter().map(|v| (v.count_ones(), *v)).collect();\n data.sort_unstable();\n return data.iter().map(|v| v.1).collect();\n }\n}\n```\n```Rust []\nimpl Solution {\n pub fn sort_by_bits(mut arr: Vec<i32>) -> Vec<i32> {\n arr.sort_unstable_by(|a, b| a.count_ones().cmp(&b.count_ones()).then(a.cmp(b)));\n return arr;\n }\n}\n```\n```python []\nclass Solution:\n def sortByBits(self, arr):\n return sorted(arr, key=lambda v: (bin(v).count(\'1\'), v)) \n```\n```Go []\nimport "math/bits"\nimport "fmt"\nimport "sort"\n\ntype num_bit struct {\n num int\n bit int\n}\n\nfunc sortByBits(arr []int) []int {\n data := make([]num_bit, len(arr), len(arr))\n \n for pos, v := range(arr) {\n data[pos] = num_bit{v, bits.OnesCount16(uint16(v))}\n }\n \n sort.Slice(data, func(i, j int) bool {\n if data[i].bit < data[j].bit {\n return true\n }\n if data[i].bit > data[j].bit {\n return false\n }\n return data[i].num < data[j].num\n })\n \n out := make([]int, len(arr), len(arr))\n for pos, v := range(data) {\n out[pos] = v.num\n }\n return out\n}\n```\n | 1 | Given two arrays `nums1` and `nums2`.
Return the maximum dot product between **non-empty** subsequences of nums1 and nums2 with the same length.
A subsequence of a array is a new array which is formed from the original array by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, `[2,3,5]` is a subsequence of `[1,2,3,4,5]` while `[1,5,3]` is not).
**Example 1:**
**Input:** nums1 = \[2,1,-2,5\], nums2 = \[3,0,-6\]
**Output:** 18
**Explanation:** Take subsequence \[2,-2\] from nums1 and subsequence \[3,-6\] from nums2.
Their dot product is (2\*3 + (-2)\*(-6)) = 18.
**Example 2:**
**Input:** nums1 = \[3,-2\], nums2 = \[2,-6,7\]
**Output:** 21
**Explanation:** Take subsequence \[3\] from nums1 and subsequence \[7\] from nums2.
Their dot product is (3\*7) = 21.
**Example 3:**
**Input:** nums1 = \[-1,-1\], nums2 = \[1,1\]
**Output:** -1
**Explanation:** Take subsequence \[-1\] from nums1 and subsequence \[1\] from nums2.
Their dot product is -1.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 500`
* `-1000 <= nums1[i], nums2[i] <= 1000` | Simulate the problem. Count the number of 1's in the binary representation of each integer. Sort by the number of 1's ascending and by the value in case of tie. |
✅ Beats 94.41 %🔥 || within 4 Lines of Code || Hash Table 🚀 || | sort-integers-by-the-number-of-1-bits | 1 | 1 | \n\n# Intuition:\n**Here we use a dictionary to store the number of 1\'s in the binary representation of each number in the array. Then we sort the keys of the dictionary and for each key we sort the values in the dictionary. Finally we return the sorted values.**\n\n# Algorithm: Hash Table\n1. Create a dictionary "D" with keys as the number of 1\'s in the binary representation of each number in the array and values as the numbers in the array.\n2. Sort the keys of the dictionary.\n3. For each key in the sorted keys of the dictionary, sort the values of the dictionary.\n4. Return the sorted values of the dictionary.\n\n# Complexity Analysis:\n- Time Complexity: **O(NlogN)** where N is the length of the array.\n- Space Complexity: **O(N)** where N is the length of the array.\n\n### Please UpVote\u2B06\uFE0F if this helps you:)\n\n# Code\n``` Python []\nfrom collections import defaultdict\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n D=defaultdict(list)\n\n for i in arr:\n D[bin(i).count(\'1\')].append(i)\n\n return [i for k in sorted(D.keys()) for i in sorted(D[k])]\n```\n``` C++ []\n#include <vector>\n#include <bitset>\n#include <unordered_map>\n#include <algorithm>\n\nclass Solution {\npublic:\n std::vector<int> sortByBits(std::vector<int>& arr) {\n std::unordered_map<int, std::vector<int>> D;\n\n for (int i : arr) {\n D[std::bitset<32>(i).count()].push_back(i);\n }\n\n std::vector<int> result;\n for (int k = 0; k <= 31; ++k) {\n if (D.find(k) != D.end()) {\n std::sort(D[k].begin(), D[k].end());\n result.insert(result.end(), D[k].begin(), D[k].end());\n }\n }\n\n return result;\n }\n};\n\n```\n``` Java []\nimport java.util.*;\n\nclass Solution {\n public int[] sortByBits(int[] arr) {\n Map<Integer, List<Integer>> D = new HashMap<>();\n\n for (int i : arr) {\n int count = Integer.bitCount(i);\n D.putIfAbsent(count, new ArrayList<>());\n D.get(count).add(i);\n }\n\n List<Integer> result = new ArrayList<>();\n List<Integer> sortedKeys = new ArrayList<>(D.keySet());\n Collections.sort(sortedKeys);\n\n for (int k : sortedKeys) {\n List<Integer> sortedValues = D.get(k);\n Collections.sort(sortedValues);\n result.addAll(sortedValues);\n }\n\n return result.stream().mapToInt(Integer::intValue).toArray();\n }\n}\n```\n``` C# []\npublic class Solution {\n public int[] SortByBits(int[] arr) {\n Dictionary<int, List<int>> D = new Dictionary<int, List<int>>();\n\n foreach (int i in arr) {\n int count = Convert.ToString(i, 2).Count(c => c == \'1\');\n if (!D.ContainsKey(count)) {\n D[count] = new List<int>();\n }\n D[count].Add(i);\n }\n\n List<int> result = new List<int>();\n foreach (var key in D.Keys.OrderBy(k => k)) {\n D[key].Sort();\n result.AddRange(D[key]);\n }\n\n return result.ToArray();\n }\n}\n\n```\n``` JavaScript []\n/**\n * @param {number[]} arr\n * @return {number[]}\n */\nvar sortByBits = function(arr) {\n const D = new Map();\n\n for (let i of arr) {\n const count = i.toString(2).split(\'1\').length - 1;\n if (!D.has(count)) {\n D.set(count, []);\n }\n D.get(count).push(i);\n }\n\n const result = [];\n for (let k of [...D.keys()].sort((a, b) => a - b)) {\n D.get(k).sort((a, b) => a - b);\n result.push(...D.get(k));\n }\n\n return result;\n};\n```\n``` TypeScript []\nfunction sortByBits(arr: number[]): number[] {\nconst D = new Map();\n\n for (let i of arr) {\n const count = i.toString(2).split(\'1\').length - 1;\n if (!D.has(count)) {\n D.set(count, []);\n }\n D.get(count).push(i);\n }\n\n const result = [];\n for (let k of [...D.keys()].sort((a, b) => a - b)) {\n D.get(k).sort((a, b) => a - b);\n result.push(...D.get(k));\n }\n\n return result;\n};\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer[] $arr\n * @return Integer[]\n */\n function sortByBits($arr) {\n $D = [];\n\n foreach ($arr as $i) {\n $count = substr_count(decbin($i), \'1\');\n if (!isset($D[$count])) {\n $D[$count] = [];\n }\n $D[$count][] = $i;\n }\n\n $result = [];\n ksort($D);\n\n foreach ($D as $values) {\n sort($values);\n $result = array_merge($result, $values);\n }\n\n return $result;\n }\n}\n```\n\n | 12 | You are given an integer array `arr`. Sort the integers in the array in ascending order by the number of `1`'s in their binary representation and in case of two or more integers have the same number of `1`'s you have to sort them in ascending order.
Return _the array after sorting it_.
**Example 1:**
**Input:** arr = \[0,1,2,3,4,5,6,7,8\]
**Output:** \[0,1,2,4,8,3,5,6,7\]
**Explantion:** \[0\] is the only integer with 0 bits.
\[1,2,4,8\] all have 1 bit.
\[3,5,6\] have 2 bits.
\[7\] has 3 bits.
The sorted array by bits is \[0,1,2,4,8,3,5,6,7\]
**Example 2:**
**Input:** arr = \[1024,512,256,128,64,32,16,8,4,2,1\]
**Output:** \[1,2,4,8,16,32,64,128,256,512,1024\]
**Explantion:** All integers have 1 bit in the binary representation, you should just sort them in ascending order.
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 104` | Consider a greedy strategy. Let’s start by making the leftmost and rightmost characters match with some number of swaps. If we figure out how to do that using the minimum number of swaps, then we can delete the leftmost and rightmost characters and solve the problem recursively. |
✅ Beats 94.41 %🔥 || within 4 Lines of Code || Hash Table 🚀 || | sort-integers-by-the-number-of-1-bits | 1 | 1 | \n\n# Intuition:\n**Here we use a dictionary to store the number of 1\'s in the binary representation of each number in the array. Then we sort the keys of the dictionary and for each key we sort the values in the dictionary. Finally we return the sorted values.**\n\n# Algorithm: Hash Table\n1. Create a dictionary "D" with keys as the number of 1\'s in the binary representation of each number in the array and values as the numbers in the array.\n2. Sort the keys of the dictionary.\n3. For each key in the sorted keys of the dictionary, sort the values of the dictionary.\n4. Return the sorted values of the dictionary.\n\n# Complexity Analysis:\n- Time Complexity: **O(NlogN)** where N is the length of the array.\n- Space Complexity: **O(N)** where N is the length of the array.\n\n### Please UpVote\u2B06\uFE0F if this helps you:)\n\n# Code\n``` Python []\nfrom collections import defaultdict\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n D=defaultdict(list)\n\n for i in arr:\n D[bin(i).count(\'1\')].append(i)\n\n return [i for k in sorted(D.keys()) for i in sorted(D[k])]\n```\n``` C++ []\n#include <vector>\n#include <bitset>\n#include <unordered_map>\n#include <algorithm>\n\nclass Solution {\npublic:\n std::vector<int> sortByBits(std::vector<int>& arr) {\n std::unordered_map<int, std::vector<int>> D;\n\n for (int i : arr) {\n D[std::bitset<32>(i).count()].push_back(i);\n }\n\n std::vector<int> result;\n for (int k = 0; k <= 31; ++k) {\n if (D.find(k) != D.end()) {\n std::sort(D[k].begin(), D[k].end());\n result.insert(result.end(), D[k].begin(), D[k].end());\n }\n }\n\n return result;\n }\n};\n\n```\n``` Java []\nimport java.util.*;\n\nclass Solution {\n public int[] sortByBits(int[] arr) {\n Map<Integer, List<Integer>> D = new HashMap<>();\n\n for (int i : arr) {\n int count = Integer.bitCount(i);\n D.putIfAbsent(count, new ArrayList<>());\n D.get(count).add(i);\n }\n\n List<Integer> result = new ArrayList<>();\n List<Integer> sortedKeys = new ArrayList<>(D.keySet());\n Collections.sort(sortedKeys);\n\n for (int k : sortedKeys) {\n List<Integer> sortedValues = D.get(k);\n Collections.sort(sortedValues);\n result.addAll(sortedValues);\n }\n\n return result.stream().mapToInt(Integer::intValue).toArray();\n }\n}\n```\n``` C# []\npublic class Solution {\n public int[] SortByBits(int[] arr) {\n Dictionary<int, List<int>> D = new Dictionary<int, List<int>>();\n\n foreach (int i in arr) {\n int count = Convert.ToString(i, 2).Count(c => c == \'1\');\n if (!D.ContainsKey(count)) {\n D[count] = new List<int>();\n }\n D[count].Add(i);\n }\n\n List<int> result = new List<int>();\n foreach (var key in D.Keys.OrderBy(k => k)) {\n D[key].Sort();\n result.AddRange(D[key]);\n }\n\n return result.ToArray();\n }\n}\n\n```\n``` JavaScript []\n/**\n * @param {number[]} arr\n * @return {number[]}\n */\nvar sortByBits = function(arr) {\n const D = new Map();\n\n for (let i of arr) {\n const count = i.toString(2).split(\'1\').length - 1;\n if (!D.has(count)) {\n D.set(count, []);\n }\n D.get(count).push(i);\n }\n\n const result = [];\n for (let k of [...D.keys()].sort((a, b) => a - b)) {\n D.get(k).sort((a, b) => a - b);\n result.push(...D.get(k));\n }\n\n return result;\n};\n```\n``` TypeScript []\nfunction sortByBits(arr: number[]): number[] {\nconst D = new Map();\n\n for (let i of arr) {\n const count = i.toString(2).split(\'1\').length - 1;\n if (!D.has(count)) {\n D.set(count, []);\n }\n D.get(count).push(i);\n }\n\n const result = [];\n for (let k of [...D.keys()].sort((a, b) => a - b)) {\n D.get(k).sort((a, b) => a - b);\n result.push(...D.get(k));\n }\n\n return result;\n};\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer[] $arr\n * @return Integer[]\n */\n function sortByBits($arr) {\n $D = [];\n\n foreach ($arr as $i) {\n $count = substr_count(decbin($i), \'1\');\n if (!isset($D[$count])) {\n $D[$count] = [];\n }\n $D[$count][] = $i;\n }\n\n $result = [];\n ksort($D);\n\n foreach ($D as $values) {\n sort($values);\n $result = array_merge($result, $values);\n }\n\n return $result;\n }\n}\n```\n\n | 12 | Given two arrays `nums1` and `nums2`.
Return the maximum dot product between **non-empty** subsequences of nums1 and nums2 with the same length.
A subsequence of a array is a new array which is formed from the original array by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, `[2,3,5]` is a subsequence of `[1,2,3,4,5]` while `[1,5,3]` is not).
**Example 1:**
**Input:** nums1 = \[2,1,-2,5\], nums2 = \[3,0,-6\]
**Output:** 18
**Explanation:** Take subsequence \[2,-2\] from nums1 and subsequence \[3,-6\] from nums2.
Their dot product is (2\*3 + (-2)\*(-6)) = 18.
**Example 2:**
**Input:** nums1 = \[3,-2\], nums2 = \[2,-6,7\]
**Output:** 21
**Explanation:** Take subsequence \[3\] from nums1 and subsequence \[7\] from nums2.
Their dot product is (3\*7) = 21.
**Example 3:**
**Input:** nums1 = \[-1,-1\], nums2 = \[1,1\]
**Output:** -1
**Explanation:** Take subsequence \[-1\] from nums1 and subsequence \[1\] from nums2.
Their dot product is -1.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 500`
* `-1000 <= nums1[i], nums2[i] <= 1000` | Simulate the problem. Count the number of 1's in the binary representation of each integer. Sort by the number of 1's ascending and by the value in case of tie. |
Beats 100% in Time Complexity | apply-discount-every-n-orders | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMaintain hashmap for product and price mapping. Then it would be pretty straight forward solution\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Cashier:\n\n def __init__(self, n: int, discount: int, products: List[int], prices: List[int]):\n self.n = n\n self.discount = discount\n self.products = products\n self.prices = prices\n self.p_p_map = self.prd_price_map()\n self.count = 0\n \n def prd_price_map(self):\n ma = {}\n for i in range(len(self.products)):\n ma[self.products[i]] = self.prices[i]\n return ma\n\n\n def getBill(self, product: List[int], amount: List[int]) -> float:\n bill = 0\n for i in range(len(product)):\n price = self.p_p_map.get(product[i])\n bill+=price*amount[i]\n self.count+=1\n if self.count%self.n==0:\n d_bill = bill * ((100 - self.discount) / 100)\n return d_bill\n return bill\n\n\n# Your Cashier object will be instantiated and called as such:\n# obj = Cashier(n, discount, products, prices)\n# param_1 = obj.getBill(product,amount)\n``` | 0 | There is a supermarket that is frequented by many customers. The products sold at the supermarket are represented as two parallel integer arrays `products` and `prices`, where the `ith` product has an ID of `products[i]` and a price of `prices[i]`.
When a customer is paying, their bill is represented as two parallel integer arrays `product` and `amount`, where the `jth` product they purchased has an ID of `product[j]`, and `amount[j]` is how much of the product they bought. Their subtotal is calculated as the sum of each `amount[j] * (price of the jth product)`.
The supermarket decided to have a sale. Every `nth` customer paying for their groceries will be given a **percentage discount**. The discount amount is given by `discount`, where they will be given `discount` percent off their subtotal. More formally, if their subtotal is `bill`, then they would actually pay `bill * ((100 - discount) / 100)`.
Implement the `Cashier` class:
* `Cashier(int n, int discount, int[] products, int[] prices)` Initializes the object with `n`, the `discount`, and the `products` and their `prices`.
* `double getBill(int[] product, int[] amount)` Returns the final total of the bill with the discount applied (if any). Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input**
\[ "Cashier ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill "\]
\[\[3,50,\[1,2,3,4,5,6,7\],\[100,200,300,400,300,200,100\]\],\[\[1,2\],\[1,2\]\],\[\[3,7\],\[10,10\]\],\[\[1,2,3,4,5,6,7\],\[1,1,1,1,1,1,1\]\],\[\[4\],\[10\]\],\[\[7,3\],\[10,10\]\],\[\[7,5,3,1,6,4,2\],\[10,10,10,9,9,9,7\]\],\[\[2,3,5\],\[5,3,2\]\]\]
**Output**
\[null,500.0,4000.0,800.0,4000.0,4000.0,7350.0,2500.0\]
**Explanation**
Cashier cashier = new Cashier(3,50,\[1,2,3,4,5,6,7\],\[100,200,300,400,300,200,100\]);
cashier.getBill(\[1,2\],\[1,2\]); // return 500.0. 1st customer, no discount.
// bill = 1 \* 100 + 2 \* 200 = 500.
cashier.getBill(\[3,7\],\[10,10\]); // return 4000.0. 2nd customer, no discount.
// bill = 10 \* 300 + 10 \* 100 = 4000.
cashier.getBill(\[1,2,3,4,5,6,7\],\[1,1,1,1,1,1,1\]); // return 800.0. 3rd customer, 50% discount.
// Original bill = 1600
// Actual bill = 1600 \* ((100 - 50) / 100) = 800.
cashier.getBill(\[4\],\[10\]); // return 4000.0. 4th customer, no discount.
cashier.getBill(\[7,3\],\[10,10\]); // return 4000.0. 5th customer, no discount.
cashier.getBill(\[7,5,3,1,6,4,2\],\[10,10,10,9,9,9,7\]); // return 7350.0. 6th customer, 50% discount.
// Original bill = 14700, but with
// Actual bill = 14700 \* ((100 - 50) / 100) = 7350.
cashier.getBill(\[2,3,5\],\[5,3,2\]); // return 2500.0. 6th customer, no discount.
**Constraints:**
* `1 <= n <= 104`
* `0 <= discount <= 100`
* `1 <= products.length <= 200`
* `prices.length == products.length`
* `1 <= products[i] <= 200`
* `1 <= prices[i] <= 1000`
* The elements in `products` are **unique**.
* `1 <= product.length <= products.length`
* `amount.length == product.length`
* `product[j]` exists in `products`.
* `1 <= amount[j] <= 1000`
* The elements of `product` are **unique**.
* At most `1000` calls will be made to `getBill`.
* Answers within `10-5` of the actual value will be accepted. | null |
Simple and clear python3 solutions | 617 ms - faster than 96.1% solutions | apply-discount-every-n-orders | 0 | 1 | # Complexity\n- Time complexity: $$O(m)$$ for `__init__` and `getBill`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nwhere `m = products.length`\n\n# Code\n``` python3 []\nclass Cashier:\n def __init__(self, n: int, discount: int, products: List[int], prices: List[int]):\n self._index = 0\n self._n = n\n self._discount = (100 - discount) / 100\n self._products = {\n pid: price\n for pid, price in zip(products, prices)\n }\n\n def getBill(self, product: List[int], amount: List[int]) -> float:\n self._index += 1\n bill = sum(\n cnt * self._products[pid]\n for pid, cnt in zip(product, amount)\n )\n if self._index % self._n == 0:\n bill *= self._discount\n return bill\n``` | 0 | There is a supermarket that is frequented by many customers. The products sold at the supermarket are represented as two parallel integer arrays `products` and `prices`, where the `ith` product has an ID of `products[i]` and a price of `prices[i]`.
When a customer is paying, their bill is represented as two parallel integer arrays `product` and `amount`, where the `jth` product they purchased has an ID of `product[j]`, and `amount[j]` is how much of the product they bought. Their subtotal is calculated as the sum of each `amount[j] * (price of the jth product)`.
The supermarket decided to have a sale. Every `nth` customer paying for their groceries will be given a **percentage discount**. The discount amount is given by `discount`, where they will be given `discount` percent off their subtotal. More formally, if their subtotal is `bill`, then they would actually pay `bill * ((100 - discount) / 100)`.
Implement the `Cashier` class:
* `Cashier(int n, int discount, int[] products, int[] prices)` Initializes the object with `n`, the `discount`, and the `products` and their `prices`.
* `double getBill(int[] product, int[] amount)` Returns the final total of the bill with the discount applied (if any). Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input**
\[ "Cashier ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill "\]
\[\[3,50,\[1,2,3,4,5,6,7\],\[100,200,300,400,300,200,100\]\],\[\[1,2\],\[1,2\]\],\[\[3,7\],\[10,10\]\],\[\[1,2,3,4,5,6,7\],\[1,1,1,1,1,1,1\]\],\[\[4\],\[10\]\],\[\[7,3\],\[10,10\]\],\[\[7,5,3,1,6,4,2\],\[10,10,10,9,9,9,7\]\],\[\[2,3,5\],\[5,3,2\]\]\]
**Output**
\[null,500.0,4000.0,800.0,4000.0,4000.0,7350.0,2500.0\]
**Explanation**
Cashier cashier = new Cashier(3,50,\[1,2,3,4,5,6,7\],\[100,200,300,400,300,200,100\]);
cashier.getBill(\[1,2\],\[1,2\]); // return 500.0. 1st customer, no discount.
// bill = 1 \* 100 + 2 \* 200 = 500.
cashier.getBill(\[3,7\],\[10,10\]); // return 4000.0. 2nd customer, no discount.
// bill = 10 \* 300 + 10 \* 100 = 4000.
cashier.getBill(\[1,2,3,4,5,6,7\],\[1,1,1,1,1,1,1\]); // return 800.0. 3rd customer, 50% discount.
// Original bill = 1600
// Actual bill = 1600 \* ((100 - 50) / 100) = 800.
cashier.getBill(\[4\],\[10\]); // return 4000.0. 4th customer, no discount.
cashier.getBill(\[7,3\],\[10,10\]); // return 4000.0. 5th customer, no discount.
cashier.getBill(\[7,5,3,1,6,4,2\],\[10,10,10,9,9,9,7\]); // return 7350.0. 6th customer, 50% discount.
// Original bill = 14700, but with
// Actual bill = 14700 \* ((100 - 50) / 100) = 7350.
cashier.getBill(\[2,3,5\],\[5,3,2\]); // return 2500.0. 6th customer, no discount.
**Constraints:**
* `1 <= n <= 104`
* `0 <= discount <= 100`
* `1 <= products.length <= 200`
* `prices.length == products.length`
* `1 <= products[i] <= 200`
* `1 <= prices[i] <= 1000`
* The elements in `products` are **unique**.
* `1 <= product.length <= products.length`
* `amount.length == product.length`
* `product[j]` exists in `products`.
* `1 <= amount[j] <= 1000`
* The elements of `product` are **unique**.
* At most `1000` calls will be made to `getBill`.
* Answers within `10-5` of the actual value will be accepted. | null |
✅ Python Simple Class Structure ✅ | apply-discount-every-n-orders | 0 | 1 | # Code\n```\nclass Cashier:\n\n def __init__(self, n: int, discount: int, products: List[int], prices: List[int]):\n self.n = n\n self.current = 0\n self.discount = discount\n self.d = {products[i]:prices[i] for i in range(len(products))}\n\n def getBill(self, product: List[int], amount: List[int]) -> float:\n self.current += 1\n suma = 0\n for i in range(len(product)):\n suma += amount[i]*self.d[product[i]]\n return suma * ((100-self.discount)/100) if self.current%self.n == 0 else suma\n\n\n\n# Your Cashier object will be instantiated and called as such:\n# obj = Cashier(n, discount, products, prices)\n# param_1 = obj.getBill(product,amount)\n``` | 0 | There is a supermarket that is frequented by many customers. The products sold at the supermarket are represented as two parallel integer arrays `products` and `prices`, where the `ith` product has an ID of `products[i]` and a price of `prices[i]`.
When a customer is paying, their bill is represented as two parallel integer arrays `product` and `amount`, where the `jth` product they purchased has an ID of `product[j]`, and `amount[j]` is how much of the product they bought. Their subtotal is calculated as the sum of each `amount[j] * (price of the jth product)`.
The supermarket decided to have a sale. Every `nth` customer paying for their groceries will be given a **percentage discount**. The discount amount is given by `discount`, where they will be given `discount` percent off their subtotal. More formally, if their subtotal is `bill`, then they would actually pay `bill * ((100 - discount) / 100)`.
Implement the `Cashier` class:
* `Cashier(int n, int discount, int[] products, int[] prices)` Initializes the object with `n`, the `discount`, and the `products` and their `prices`.
* `double getBill(int[] product, int[] amount)` Returns the final total of the bill with the discount applied (if any). Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input**
\[ "Cashier ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill "\]
\[\[3,50,\[1,2,3,4,5,6,7\],\[100,200,300,400,300,200,100\]\],\[\[1,2\],\[1,2\]\],\[\[3,7\],\[10,10\]\],\[\[1,2,3,4,5,6,7\],\[1,1,1,1,1,1,1\]\],\[\[4\],\[10\]\],\[\[7,3\],\[10,10\]\],\[\[7,5,3,1,6,4,2\],\[10,10,10,9,9,9,7\]\],\[\[2,3,5\],\[5,3,2\]\]\]
**Output**
\[null,500.0,4000.0,800.0,4000.0,4000.0,7350.0,2500.0\]
**Explanation**
Cashier cashier = new Cashier(3,50,\[1,2,3,4,5,6,7\],\[100,200,300,400,300,200,100\]);
cashier.getBill(\[1,2\],\[1,2\]); // return 500.0. 1st customer, no discount.
// bill = 1 \* 100 + 2 \* 200 = 500.
cashier.getBill(\[3,7\],\[10,10\]); // return 4000.0. 2nd customer, no discount.
// bill = 10 \* 300 + 10 \* 100 = 4000.
cashier.getBill(\[1,2,3,4,5,6,7\],\[1,1,1,1,1,1,1\]); // return 800.0. 3rd customer, 50% discount.
// Original bill = 1600
// Actual bill = 1600 \* ((100 - 50) / 100) = 800.
cashier.getBill(\[4\],\[10\]); // return 4000.0. 4th customer, no discount.
cashier.getBill(\[7,3\],\[10,10\]); // return 4000.0. 5th customer, no discount.
cashier.getBill(\[7,5,3,1,6,4,2\],\[10,10,10,9,9,9,7\]); // return 7350.0. 6th customer, 50% discount.
// Original bill = 14700, but with
// Actual bill = 14700 \* ((100 - 50) / 100) = 7350.
cashier.getBill(\[2,3,5\],\[5,3,2\]); // return 2500.0. 6th customer, no discount.
**Constraints:**
* `1 <= n <= 104`
* `0 <= discount <= 100`
* `1 <= products.length <= 200`
* `prices.length == products.length`
* `1 <= products[i] <= 200`
* `1 <= prices[i] <= 1000`
* The elements in `products` are **unique**.
* `1 <= product.length <= products.length`
* `amount.length == product.length`
* `product[j]` exists in `products`.
* `1 <= amount[j] <= 1000`
* The elements of `product` are **unique**.
* At most `1000` calls will be made to `getBill`.
* Answers within `10-5` of the actual value will be accepted. | null |
Python Easy solution using dict | apply-discount-every-n-orders | 0 | 1 | ```\nclass Cashier:\n\n def __init__(self, n: int, discount: int, products: List[int], prices: List[int]):\n self.dis = discount / 100\n self.currentCustomer = 0\n self.n = n\n self.products = {i: j for i, j in zip(products, prices)}\n\n def getBill(self, product: List[int], amount: List[int]) -> float:\n self.currentCustomer += 1\n bill = sum([(self.products[i] * j) for i, j in zip(product, amount)])\n return bill * (1 - self.dis) if self.currentCustomer % self.n == 0 else bill\n\n\n# Your Cashier object will be instantiated and called as such:\n# obj = Cashier(n, discount, products, prices)\n# param_1 = obj.getBill(product,amount)\n``` | 0 | There is a supermarket that is frequented by many customers. The products sold at the supermarket are represented as two parallel integer arrays `products` and `prices`, where the `ith` product has an ID of `products[i]` and a price of `prices[i]`.
When a customer is paying, their bill is represented as two parallel integer arrays `product` and `amount`, where the `jth` product they purchased has an ID of `product[j]`, and `amount[j]` is how much of the product they bought. Their subtotal is calculated as the sum of each `amount[j] * (price of the jth product)`.
The supermarket decided to have a sale. Every `nth` customer paying for their groceries will be given a **percentage discount**. The discount amount is given by `discount`, where they will be given `discount` percent off their subtotal. More formally, if their subtotal is `bill`, then they would actually pay `bill * ((100 - discount) / 100)`.
Implement the `Cashier` class:
* `Cashier(int n, int discount, int[] products, int[] prices)` Initializes the object with `n`, the `discount`, and the `products` and their `prices`.
* `double getBill(int[] product, int[] amount)` Returns the final total of the bill with the discount applied (if any). Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input**
\[ "Cashier ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill "\]
\[\[3,50,\[1,2,3,4,5,6,7\],\[100,200,300,400,300,200,100\]\],\[\[1,2\],\[1,2\]\],\[\[3,7\],\[10,10\]\],\[\[1,2,3,4,5,6,7\],\[1,1,1,1,1,1,1\]\],\[\[4\],\[10\]\],\[\[7,3\],\[10,10\]\],\[\[7,5,3,1,6,4,2\],\[10,10,10,9,9,9,7\]\],\[\[2,3,5\],\[5,3,2\]\]\]
**Output**
\[null,500.0,4000.0,800.0,4000.0,4000.0,7350.0,2500.0\]
**Explanation**
Cashier cashier = new Cashier(3,50,\[1,2,3,4,5,6,7\],\[100,200,300,400,300,200,100\]);
cashier.getBill(\[1,2\],\[1,2\]); // return 500.0. 1st customer, no discount.
// bill = 1 \* 100 + 2 \* 200 = 500.
cashier.getBill(\[3,7\],\[10,10\]); // return 4000.0. 2nd customer, no discount.
// bill = 10 \* 300 + 10 \* 100 = 4000.
cashier.getBill(\[1,2,3,4,5,6,7\],\[1,1,1,1,1,1,1\]); // return 800.0. 3rd customer, 50% discount.
// Original bill = 1600
// Actual bill = 1600 \* ((100 - 50) / 100) = 800.
cashier.getBill(\[4\],\[10\]); // return 4000.0. 4th customer, no discount.
cashier.getBill(\[7,3\],\[10,10\]); // return 4000.0. 5th customer, no discount.
cashier.getBill(\[7,5,3,1,6,4,2\],\[10,10,10,9,9,9,7\]); // return 7350.0. 6th customer, 50% discount.
// Original bill = 14700, but with
// Actual bill = 14700 \* ((100 - 50) / 100) = 7350.
cashier.getBill(\[2,3,5\],\[5,3,2\]); // return 2500.0. 6th customer, no discount.
**Constraints:**
* `1 <= n <= 104`
* `0 <= discount <= 100`
* `1 <= products.length <= 200`
* `prices.length == products.length`
* `1 <= products[i] <= 200`
* `1 <= prices[i] <= 1000`
* The elements in `products` are **unique**.
* `1 <= product.length <= products.length`
* `amount.length == product.length`
* `product[j]` exists in `products`.
* `1 <= amount[j] <= 1000`
* The elements of `product` are **unique**.
* At most `1000` calls will be made to `getBill`.
* Answers within `10-5` of the actual value will be accepted. | null |
[Python3] Good enough | apply-discount-every-n-orders | 0 | 1 | ``` Python3 []\nclass Cashier:\n\n def __init__(self, n: int, discount: int, products: List[int], prices: List[int]):\n self.lucky = n\n self.discount = discount\n self.costs = {}\n self.customers = 0\n\n for i in range(len(products)):\n self.costs[products[i]] = prices[i]\n \n\n def getBill(self, product: List[int], amount: List[int]) -> float:\n self.customers += 1\n\n bill = sum(self.costs[product[i]]*amount[i] for i in range(len(product)))\n\n if self.customers % self.lucky == 0:\n bill *= (100-self.discount) / 100\n \n return bill\n \n\n\n# Your Cashier object will be instantiated and called as such:\n# obj = Cashier(n, discount, products, prices)\n# param_1 = obj.getBill(product,amount)\n``` | 0 | There is a supermarket that is frequented by many customers. The products sold at the supermarket are represented as two parallel integer arrays `products` and `prices`, where the `ith` product has an ID of `products[i]` and a price of `prices[i]`.
When a customer is paying, their bill is represented as two parallel integer arrays `product` and `amount`, where the `jth` product they purchased has an ID of `product[j]`, and `amount[j]` is how much of the product they bought. Their subtotal is calculated as the sum of each `amount[j] * (price of the jth product)`.
The supermarket decided to have a sale. Every `nth` customer paying for their groceries will be given a **percentage discount**. The discount amount is given by `discount`, where they will be given `discount` percent off their subtotal. More formally, if their subtotal is `bill`, then they would actually pay `bill * ((100 - discount) / 100)`.
Implement the `Cashier` class:
* `Cashier(int n, int discount, int[] products, int[] prices)` Initializes the object with `n`, the `discount`, and the `products` and their `prices`.
* `double getBill(int[] product, int[] amount)` Returns the final total of the bill with the discount applied (if any). Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input**
\[ "Cashier ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill "\]
\[\[3,50,\[1,2,3,4,5,6,7\],\[100,200,300,400,300,200,100\]\],\[\[1,2\],\[1,2\]\],\[\[3,7\],\[10,10\]\],\[\[1,2,3,4,5,6,7\],\[1,1,1,1,1,1,1\]\],\[\[4\],\[10\]\],\[\[7,3\],\[10,10\]\],\[\[7,5,3,1,6,4,2\],\[10,10,10,9,9,9,7\]\],\[\[2,3,5\],\[5,3,2\]\]\]
**Output**
\[null,500.0,4000.0,800.0,4000.0,4000.0,7350.0,2500.0\]
**Explanation**
Cashier cashier = new Cashier(3,50,\[1,2,3,4,5,6,7\],\[100,200,300,400,300,200,100\]);
cashier.getBill(\[1,2\],\[1,2\]); // return 500.0. 1st customer, no discount.
// bill = 1 \* 100 + 2 \* 200 = 500.
cashier.getBill(\[3,7\],\[10,10\]); // return 4000.0. 2nd customer, no discount.
// bill = 10 \* 300 + 10 \* 100 = 4000.
cashier.getBill(\[1,2,3,4,5,6,7\],\[1,1,1,1,1,1,1\]); // return 800.0. 3rd customer, 50% discount.
// Original bill = 1600
// Actual bill = 1600 \* ((100 - 50) / 100) = 800.
cashier.getBill(\[4\],\[10\]); // return 4000.0. 4th customer, no discount.
cashier.getBill(\[7,3\],\[10,10\]); // return 4000.0. 5th customer, no discount.
cashier.getBill(\[7,5,3,1,6,4,2\],\[10,10,10,9,9,9,7\]); // return 7350.0. 6th customer, 50% discount.
// Original bill = 14700, but with
// Actual bill = 14700 \* ((100 - 50) / 100) = 7350.
cashier.getBill(\[2,3,5\],\[5,3,2\]); // return 2500.0. 6th customer, no discount.
**Constraints:**
* `1 <= n <= 104`
* `0 <= discount <= 100`
* `1 <= products.length <= 200`
* `prices.length == products.length`
* `1 <= products[i] <= 200`
* `1 <= prices[i] <= 1000`
* The elements in `products` are **unique**.
* `1 <= product.length <= products.length`
* `amount.length == product.length`
* `product[j]` exists in `products`.
* `1 <= amount[j] <= 1000`
* The elements of `product` are **unique**.
* At most `1000` calls will be made to `getBill`.
* Answers within `10-5` of the actual value will be accepted. | null |
Python clear solution. | apply-discount-every-n-orders | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nThat\'s pretty much self-explanatory. Store the prices in dictionary for speed.\nValue "c" counts if it\'s time to give a discount.\n\n\n# Code\n```\nclass Cashier:\n\n def __init__(self, n: int, discount: int, products: List[int], prices: List[int]):\n self.n = n\n self.c = 1\n self.d = discount\n self.cat = {x:y for (x,y) in zip(products,prices)}\n\n \n\n def getBill(self, product: List[int], amount: List[int]) -> float:\n res = 0\n for i in range(len(amount)):\n res += self.cat[product[i]]*amount[i]\n if self.c == self.n:\n res *= (100-self.d)/100\n self.c =1\n else: self.c +=1\n return res\n\n\n\n\n# Your Cashier object will be instantiated and called as such:\n# obj = Cashier(n, discount, products, prices)\n# param_1 = obj.getBill(product,amount)\n``` | 0 | There is a supermarket that is frequented by many customers. The products sold at the supermarket are represented as two parallel integer arrays `products` and `prices`, where the `ith` product has an ID of `products[i]` and a price of `prices[i]`.
When a customer is paying, their bill is represented as two parallel integer arrays `product` and `amount`, where the `jth` product they purchased has an ID of `product[j]`, and `amount[j]` is how much of the product they bought. Their subtotal is calculated as the sum of each `amount[j] * (price of the jth product)`.
The supermarket decided to have a sale. Every `nth` customer paying for their groceries will be given a **percentage discount**. The discount amount is given by `discount`, where they will be given `discount` percent off their subtotal. More formally, if their subtotal is `bill`, then they would actually pay `bill * ((100 - discount) / 100)`.
Implement the `Cashier` class:
* `Cashier(int n, int discount, int[] products, int[] prices)` Initializes the object with `n`, the `discount`, and the `products` and their `prices`.
* `double getBill(int[] product, int[] amount)` Returns the final total of the bill with the discount applied (if any). Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input**
\[ "Cashier ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill ", "getBill "\]
\[\[3,50,\[1,2,3,4,5,6,7\],\[100,200,300,400,300,200,100\]\],\[\[1,2\],\[1,2\]\],\[\[3,7\],\[10,10\]\],\[\[1,2,3,4,5,6,7\],\[1,1,1,1,1,1,1\]\],\[\[4\],\[10\]\],\[\[7,3\],\[10,10\]\],\[\[7,5,3,1,6,4,2\],\[10,10,10,9,9,9,7\]\],\[\[2,3,5\],\[5,3,2\]\]\]
**Output**
\[null,500.0,4000.0,800.0,4000.0,4000.0,7350.0,2500.0\]
**Explanation**
Cashier cashier = new Cashier(3,50,\[1,2,3,4,5,6,7\],\[100,200,300,400,300,200,100\]);
cashier.getBill(\[1,2\],\[1,2\]); // return 500.0. 1st customer, no discount.
// bill = 1 \* 100 + 2 \* 200 = 500.
cashier.getBill(\[3,7\],\[10,10\]); // return 4000.0. 2nd customer, no discount.
// bill = 10 \* 300 + 10 \* 100 = 4000.
cashier.getBill(\[1,2,3,4,5,6,7\],\[1,1,1,1,1,1,1\]); // return 800.0. 3rd customer, 50% discount.
// Original bill = 1600
// Actual bill = 1600 \* ((100 - 50) / 100) = 800.
cashier.getBill(\[4\],\[10\]); // return 4000.0. 4th customer, no discount.
cashier.getBill(\[7,3\],\[10,10\]); // return 4000.0. 5th customer, no discount.
cashier.getBill(\[7,5,3,1,6,4,2\],\[10,10,10,9,9,9,7\]); // return 7350.0. 6th customer, 50% discount.
// Original bill = 14700, but with
// Actual bill = 14700 \* ((100 - 50) / 100) = 7350.
cashier.getBill(\[2,3,5\],\[5,3,2\]); // return 2500.0. 6th customer, no discount.
**Constraints:**
* `1 <= n <= 104`
* `0 <= discount <= 100`
* `1 <= products.length <= 200`
* `prices.length == products.length`
* `1 <= products[i] <= 200`
* `1 <= prices[i] <= 1000`
* The elements in `products` are **unique**.
* `1 <= product.length <= products.length`
* `amount.length == product.length`
* `product[j]` exists in `products`.
* `1 <= amount[j] <= 1000`
* The elements of `product` are **unique**.
* At most `1000` calls will be made to `getBill`.
* Answers within `10-5` of the actual value will be accepted. | null |
Sliding Window - O(n) | number-of-substrings-containing-all-three-characters | 0 | 1 | # Approach\n1) Move the window from 0->n, with incrementing the character count in map/dict\n2) When count of each chars in dict is set [could be =1 or >1], we have a valid substring\n3) From valid substring\'s end [window end /right pointer], count how many other substrings are possible and add it to result\n\nDry Run of 1 case:\nGiven s=\'abcabc\'\n\nAt index=2, dict={a:1,b:1,c:1}\nright pointer = 2\nlength of s = 6 \n\nTotal substrings possible from index 3 to end?\nlength of s - right => 6-2 = 4\n\nWhich 4 substirngs?\n\'abc\' [the one we got when dict is set]\n\n[Remaining substring\'s]\n\'abc\'a\n\'abc\'ab\n\'abc\'abc\n\n\n\n\n# Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(3) ->\n\n# Code\n```\nclass Solution:\n def numberOfSubstrings(self, s: str) -> int:\n dict_cnt={\'a\':0,\'b\':0,\'c\':0}\n n=len(s)\n left=0\n res=0\n\n for right in range(len(s)):\n dict_cnt[s[right]]+=1\n while(dict_cnt[\'a\'] and dict_cnt[\'b\'] and dict_cnt[\'c\']):\n res+=n-right\n dict_cnt[s[left]]-=1\n left+=1\n\n return res\n \n``` | 4 | Given a string `s` consisting only of characters _a_, _b_ and _c_.
Return the number of substrings containing **at least** one occurrence of all these characters _a_, _b_ and _c_.
**Example 1:**
**Input:** s = "abcabc "
**Output:** 10
**Explanation:** The substrings containing at least one occurrence of the characters _a_, _b_ and _c are "_abc _", "_abca _", "_abcab _", "_abcabc _", "_bca _", "_bcab _", "_bcabc _", "_cab _", "_cabc _"_ and _"_abc _"_ (**again**)_._
**Example 2:**
**Input:** s = "aaacb "
**Output:** 3
**Explanation:** The substrings containing at least one occurrence of the characters _a_, _b_ and _c are "_aaacb _", "_aacb _"_ and _"_acb _"._
**Example 3:**
**Input:** s = "abc "
**Output:** 1
**Constraints:**
* `3 <= s.length <= 5 x 10^4`
* `s` only consists of _a_, _b_ or _c_ characters. | Loop over 1 ≤ x,y ≤ 1000 and check if f(x,y) == z. |
Sliding Window - O(n) | number-of-substrings-containing-all-three-characters | 0 | 1 | # Approach\n1) Move the window from 0->n, with incrementing the character count in map/dict\n2) When count of each chars in dict is set [could be =1 or >1], we have a valid substring\n3) From valid substring\'s end [window end /right pointer], count how many other substrings are possible and add it to result\n\nDry Run of 1 case:\nGiven s=\'abcabc\'\n\nAt index=2, dict={a:1,b:1,c:1}\nright pointer = 2\nlength of s = 6 \n\nTotal substrings possible from index 3 to end?\nlength of s - right => 6-2 = 4\n\nWhich 4 substirngs?\n\'abc\' [the one we got when dict is set]\n\n[Remaining substring\'s]\n\'abc\'a\n\'abc\'ab\n\'abc\'abc\n\n\n\n\n# Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(3) ->\n\n# Code\n```\nclass Solution:\n def numberOfSubstrings(self, s: str) -> int:\n dict_cnt={\'a\':0,\'b\':0,\'c\':0}\n n=len(s)\n left=0\n res=0\n\n for right in range(len(s)):\n dict_cnt[s[right]]+=1\n while(dict_cnt[\'a\'] and dict_cnt[\'b\'] and dict_cnt[\'c\']):\n res+=n-right\n dict_cnt[s[left]]-=1\n left+=1\n\n return res\n \n``` | 4 | You are given two integer arrays of equal length `target` and `arr`. In one step, you can select any **non-empty subarray** of `arr` and reverse it. You are allowed to make any number of steps.
Return `true` _if you can make_ `arr` _equal to_ `target` _or_ `false` _otherwise_.
**Example 1:**
**Input:** target = \[1,2,3,4\], arr = \[2,4,1,3\]
**Output:** true
**Explanation:** You can follow the next steps to convert arr to target:
1- Reverse subarray \[2,4,1\], arr becomes \[1,4,2,3\]
2- Reverse subarray \[4,2\], arr becomes \[1,2,4,3\]
3- Reverse subarray \[4,3\], arr becomes \[1,2,3,4\]
There are multiple ways to convert arr to target, this is not the only way to do so.
**Example 2:**
**Input:** target = \[7\], arr = \[7\]
**Output:** true
**Explanation:** arr is equal to target without any reverses.
**Example 3:**
**Input:** target = \[3,7,9\], arr = \[3,7,11\]
**Output:** false
**Explanation:** arr does not have value 9 and it can never be converted to target.
**Constraints:**
* `target.length == arr.length`
* `1 <= target.length <= 1000`
* `1 <= target[i] <= 1000`
* `1 <= arr[i] <= 1000` | For each position we simply need to find the first occurrence of a/b/c on or after this position. So we can pre-compute three link-list of indices of each a, b, and c. |
Python 3 | Two Pointers | Explanation | number-of-substrings-containing-all-three-characters | 0 | 1 | ### Explanation\n- Two pointer to same direction, fast pointer check new character, slow pointer shorten substr\n- Use a little math (`n-j`) to count possible valid substrings\n- Check comments for more detail\n### Implementation\n```\nclass Solution:\n def numberOfSubstrings(self, s: str) -> int:\n a = b = c = 0 # counter for letter a/b/c\n ans, i, n = 0, 0, len(s) # i: slow pointer\n for j, letter in enumerate(s): # j: fast pointer\n if letter == \'a\': a += 1 # increment a/b/c accordingly\n elif letter == \'b\': b += 1\n else: c += 1\n while a > 0 and b > 0 and c > 0: # if all of a/b/c are contained, move slow pointer\n ans += n-j # count possible substr, if a substr ends at j, then there are n-j substrs to the right that are containing all a/b/c\n if s[i] == \'a\': a -= 1 # decrement counter accordingly\n elif s[i] == \'b\': b -= 1\n else: c -= 1\n i += 1 # move slow pointer\n return ans \n``` | 35 | Given a string `s` consisting only of characters _a_, _b_ and _c_.
Return the number of substrings containing **at least** one occurrence of all these characters _a_, _b_ and _c_.
**Example 1:**
**Input:** s = "abcabc "
**Output:** 10
**Explanation:** The substrings containing at least one occurrence of the characters _a_, _b_ and _c are "_abc _", "_abca _", "_abcab _", "_abcabc _", "_bca _", "_bcab _", "_bcabc _", "_cab _", "_cabc _"_ and _"_abc _"_ (**again**)_._
**Example 2:**
**Input:** s = "aaacb "
**Output:** 3
**Explanation:** The substrings containing at least one occurrence of the characters _a_, _b_ and _c are "_aaacb _", "_aacb _"_ and _"_acb _"._
**Example 3:**
**Input:** s = "abc "
**Output:** 1
**Constraints:**
* `3 <= s.length <= 5 x 10^4`
* `s` only consists of _a_, _b_ or _c_ characters. | Loop over 1 ≤ x,y ≤ 1000 and check if f(x,y) == z. |
Python 3 | Two Pointers | Explanation | number-of-substrings-containing-all-three-characters | 0 | 1 | ### Explanation\n- Two pointer to same direction, fast pointer check new character, slow pointer shorten substr\n- Use a little math (`n-j`) to count possible valid substrings\n- Check comments for more detail\n### Implementation\n```\nclass Solution:\n def numberOfSubstrings(self, s: str) -> int:\n a = b = c = 0 # counter for letter a/b/c\n ans, i, n = 0, 0, len(s) # i: slow pointer\n for j, letter in enumerate(s): # j: fast pointer\n if letter == \'a\': a += 1 # increment a/b/c accordingly\n elif letter == \'b\': b += 1\n else: c += 1\n while a > 0 and b > 0 and c > 0: # if all of a/b/c are contained, move slow pointer\n ans += n-j # count possible substr, if a substr ends at j, then there are n-j substrs to the right that are containing all a/b/c\n if s[i] == \'a\': a -= 1 # decrement counter accordingly\n elif s[i] == \'b\': b -= 1\n else: c -= 1\n i += 1 # move slow pointer\n return ans \n``` | 35 | You are given two integer arrays of equal length `target` and `arr`. In one step, you can select any **non-empty subarray** of `arr` and reverse it. You are allowed to make any number of steps.
Return `true` _if you can make_ `arr` _equal to_ `target` _or_ `false` _otherwise_.
**Example 1:**
**Input:** target = \[1,2,3,4\], arr = \[2,4,1,3\]
**Output:** true
**Explanation:** You can follow the next steps to convert arr to target:
1- Reverse subarray \[2,4,1\], arr becomes \[1,4,2,3\]
2- Reverse subarray \[4,2\], arr becomes \[1,2,4,3\]
3- Reverse subarray \[4,3\], arr becomes \[1,2,3,4\]
There are multiple ways to convert arr to target, this is not the only way to do so.
**Example 2:**
**Input:** target = \[7\], arr = \[7\]
**Output:** true
**Explanation:** arr is equal to target without any reverses.
**Example 3:**
**Input:** target = \[3,7,9\], arr = \[3,7,11\]
**Output:** false
**Explanation:** arr does not have value 9 and it can never be converted to target.
**Constraints:**
* `target.length == arr.length`
* `1 <= target.length <= 1000`
* `1 <= target[i] <= 1000`
* `1 <= arr[i] <= 1000` | For each position we simply need to find the first occurrence of a/b/c on or after this position. So we can pre-compute three link-list of indices of each a, b, and c. |
Simple Solution || Beginner Friendly || Easy to Understand || O(n) 🔥 | count-all-valid-pickup-and-delivery-options | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nYou have `n` items to be delivered, and you need to find the number of different valid orders in which you can deliver these items.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDynamic Programming Approach:\n- Initialize an array `dp` of size `n + 1` to store the number of valid orders for each value of `n`. Initialize `dp[0] to 1` because there\'s only one valid order when there are no items to deliver (an empty order).\n- Loop from `i = 1` to n to fill the dp array for all values of n. For each i, do the following:\n a. Calculate the value of `k` as `i * (i + (i - 1))`. This represents the number of ways you can arrange the items for the current `i`.\n\n b. Update` dp[i]` as the product of `dp[i-1]` and `k`, modulo 1000000007. This step accounts for the additional ways to arrange items when you add the `i-th` item to the previous valid orders.\n- After the loop completes, the dp array will contain the number of valid orders for each `n`.\n- Finally, return dp[n] as the result, casting it to an integer.\n# Complexity\n- Time complexity: `O(n)`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(n)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int countOrders(int n) {\n long[] dp = new long[n + 1];\n dp[0] = 1;\n \n for (int i = 1; i < dp.length; i++) {\n long k = i * (i + (i - 1));\n dp[i] = (dp[i - 1] * k) % 1000000007;\n }\n return (int) dp[dp.length - 1];\n }\n}\n```\n```python3 []\nclass Solution:\n def countOrders(self, n: int) -> int:\n \n dp = [0] * (n+1)\n dp[1] = 1\n \n for i in range(2, n+1):\n dp[i] = (i * dp[i-1] * (2*i - 1)) % (10 ** 9 + 7)\n \n return dp[n]\n```\n```C++ []\nclass Solution {\npublic:\n int countOrders(int n) {\n vector<long long> dp(n + 1);\n dp[0] = 1;\n\n for (int i = 1; i <= n; i++) {\n long long k = i * (i + (i - 1));\n dp[i] = (dp[i - 1] * k) % 1000000007;\n }\n\n return static_cast<int>(dp[n]);\n }\n};\n```\n\n```python []\nclass Solution:\n def countOrders(self, n: int) -> int:\n ans = 1\n for n in range(2, n + 1):\n ans *= n*(2*n-1)\n ans %= 1_000_000_007\n return ans \n```\n```C []\nint countOrders(int n)\n {\n long long dp[502];\n dp[0] = 0;\n dp[1] = 1;\n \n long long res = 0;\n \n for(int i = 2; i <= n; i++)\n {\n long long prev = dp[i-1];\n long long pos = 2 + ((i-1) * 2) - 1;\n dp[i] = (pos * prev * i) % 1000000007;\n }\n \n return dp[n];\n }\n```\n | 10 | Given `n` orders, each order consist in pickup and delivery services.
Count all valid pickup/delivery possible sequences such that delivery(i) is always after of pickup(i).
Since the answer may be too large, return it modulo 10^9 + 7.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation:** Unique order (P1, D1), Delivery 1 always is after of Pickup 1.
**Example 2:**
**Input:** n = 2
**Output:** 6
**Explanation:** All possible orders:
(P1,P2,D1,D2), (P1,P2,D2,D1), (P1,D1,P2,D2), (P2,P1,D1,D2), (P2,P1,D2,D1) and (P2,D2,P1,D1).
This is an invalid order (P1,D2,P2,D1) because Pickup 2 is after of Delivery 2.
**Example 3:**
**Input:** n = 3
**Output:** 90
**Constraints:**
* `1 <= n <= 500`
Given 2 integers n and start. Your task is return any permutation p of (0,1,2.....,2^n -1) such that : p\[0\] = start, p\[i\] and p\[i+1\] differ by only one bit for all 0 <= i < 2^n - 1. | Use gray code to generate a n-bit sequence. Rotate the sequence such that its first element is start. |
Simple Solution || Beginner Friendly || Easy to Understand || O(n) 🔥 | count-all-valid-pickup-and-delivery-options | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nYou have `n` items to be delivered, and you need to find the number of different valid orders in which you can deliver these items.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDynamic Programming Approach:\n- Initialize an array `dp` of size `n + 1` to store the number of valid orders for each value of `n`. Initialize `dp[0] to 1` because there\'s only one valid order when there are no items to deliver (an empty order).\n- Loop from `i = 1` to n to fill the dp array for all values of n. For each i, do the following:\n a. Calculate the value of `k` as `i * (i + (i - 1))`. This represents the number of ways you can arrange the items for the current `i`.\n\n b. Update` dp[i]` as the product of `dp[i-1]` and `k`, modulo 1000000007. This step accounts for the additional ways to arrange items when you add the `i-th` item to the previous valid orders.\n- After the loop completes, the dp array will contain the number of valid orders for each `n`.\n- Finally, return dp[n] as the result, casting it to an integer.\n# Complexity\n- Time complexity: `O(n)`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(n)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int countOrders(int n) {\n long[] dp = new long[n + 1];\n dp[0] = 1;\n \n for (int i = 1; i < dp.length; i++) {\n long k = i * (i + (i - 1));\n dp[i] = (dp[i - 1] * k) % 1000000007;\n }\n return (int) dp[dp.length - 1];\n }\n}\n```\n```python3 []\nclass Solution:\n def countOrders(self, n: int) -> int:\n \n dp = [0] * (n+1)\n dp[1] = 1\n \n for i in range(2, n+1):\n dp[i] = (i * dp[i-1] * (2*i - 1)) % (10 ** 9 + 7)\n \n return dp[n]\n```\n```C++ []\nclass Solution {\npublic:\n int countOrders(int n) {\n vector<long long> dp(n + 1);\n dp[0] = 1;\n\n for (int i = 1; i <= n; i++) {\n long long k = i * (i + (i - 1));\n dp[i] = (dp[i - 1] * k) % 1000000007;\n }\n\n return static_cast<int>(dp[n]);\n }\n};\n```\n\n```python []\nclass Solution:\n def countOrders(self, n: int) -> int:\n ans = 1\n for n in range(2, n + 1):\n ans *= n*(2*n-1)\n ans %= 1_000_000_007\n return ans \n```\n```C []\nint countOrders(int n)\n {\n long long dp[502];\n dp[0] = 0;\n dp[1] = 1;\n \n long long res = 0;\n \n for(int i = 2; i <= n; i++)\n {\n long long prev = dp[i-1];\n long long pos = 2 + ((i-1) * 2) - 1;\n dp[i] = (pos * prev * i) % 1000000007;\n }\n \n return dp[n];\n }\n```\n | 10 | Given a binary string `s` and an integer `k`, return `true` _if every binary code of length_ `k` _is a substring of_ `s`. Otherwise, return `false`.
**Example 1:**
**Input:** s = "00110110 ", k = 2
**Output:** true
**Explanation:** The binary codes of length 2 are "00 ", "01 ", "10 " and "11 ". They can be all found as substrings at indices 0, 1, 3 and 2 respectively.
**Example 2:**
**Input:** s = "0110 ", k = 1
**Output:** true
**Explanation:** The binary codes of length 1 are "0 " and "1 ", it is clear that both exist as a substring.
**Example 3:**
**Input:** s = "0110 ", k = 2
**Output:** false
**Explanation:** The binary code "00 " is of length 2 and does not exist in the array.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= k <= 20` | Use the permutation and combination theory to add one (P, D) pair each time until n pairs. |
C++/Python Math recursion->1 loop->1 line | count-all-valid-pickup-and-delivery-options | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is a permutation problem.\n$$\nF(n)=\\frac{(2n)!}{2^n}\n$$\nUse the recurrence\n$$\nF(n+1)=F(n)\\times(n+1)\\times (2n+1)\n$$\n# Approach\n<!-- Describe your approach to solving the problem. -->\n[Please turn on English subtitles if necessary]\n[https://youtu.be/erH5HQf24J4?si=nG8Pde5LRuwpI8hF](https://youtu.be/erH5HQf24J4?si=nG8Pde5LRuwpI8hF)\nThere are (2n) objects to arrange in a list.\nSo there are (2n)! ways to permute without any constraints. Consider the following 2 sequences\n```\n****************Pi*********Di**********\n****************Di*********Pi**********\n```\nwhere both are identical except for Pi & Di.\nBut every pair $(P_i, D_i)$ must be in this order. So 1/2 of them follow this order. There are n pairs. So the number for valid sequences is\n$$\nF(n)=\\frac{(2n)!}{2^n}\n$$\n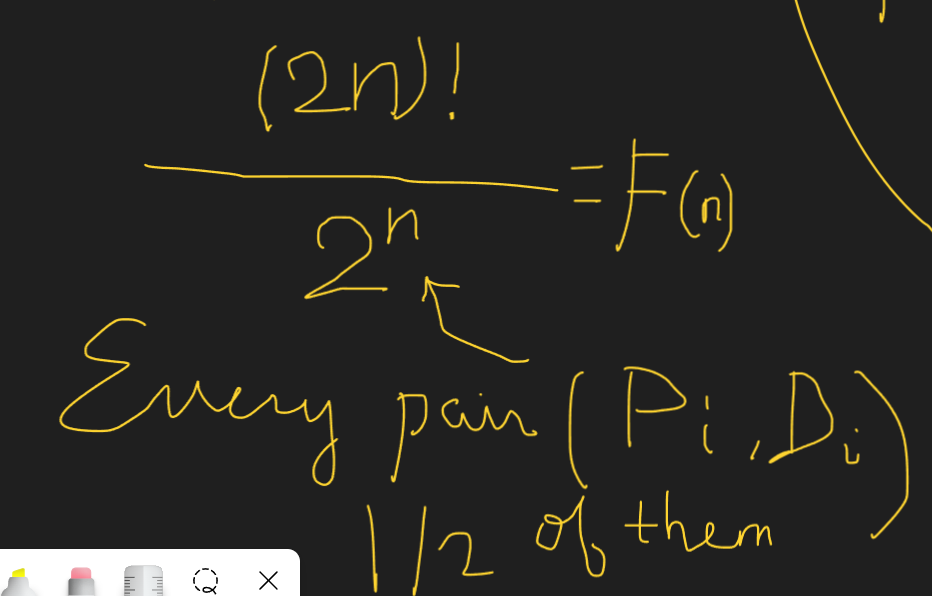\n# How Recursion?\nOne way is to compare $F(n)$ & $F(n+1)$ using $\nF(n)=\\frac{(2n)!}{2^n}\n$.\nThere is still other way using combination.\nOne wants to place the pair $(P_{n+1}, D_{n+1})$ in $(2n+2)$ positions. There are \n$$\nC^{2n+2}_2=(n+1)\\times (2n+1)\n$$\nways for placing this pair. Using multiplication principle for counting, the rest is arranging $(P_i, D_i) \\ (i=1,\\dots n) $ with number $F(n)$. So one has\n$$\nF(n+1)=F(n)\\times(n+1)\\times (2n+1)\n$$\nwith the initial case $F(1)=1$.\n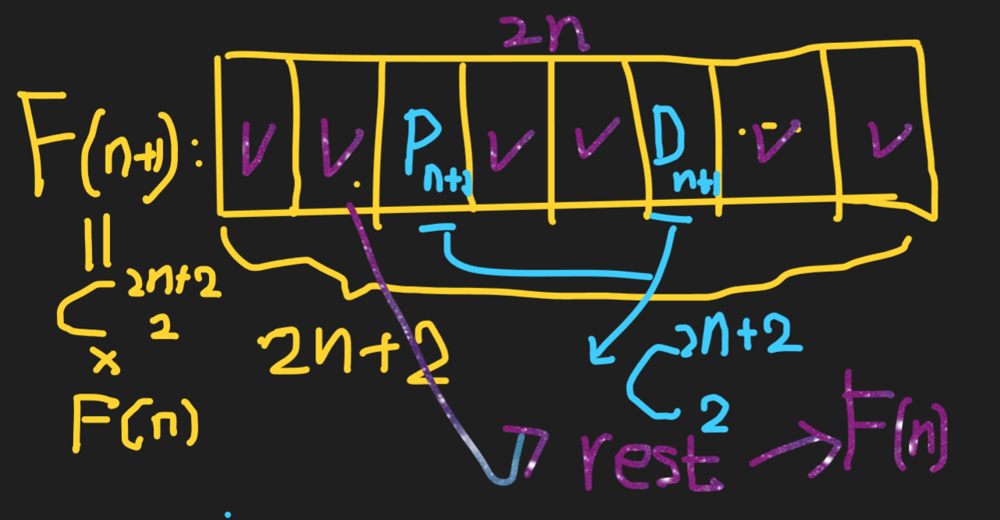\n# 1 line solution\n[https://youtu.be/enZbhnVRuLk?si=E_NanOduoKKMN7u1](https://youtu.be/enZbhnVRuLk?si=E_NanOduoKKMN7u1)\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code\n```\nclass Solution {\npublic:\n const int mod=1e9+7;\n int countOrders(int n) {\n long long num=1;\n for(long long i=1; i<n; i++){\n num=(num*(i+1)*(2*i+1)%mod);\n }\n return num;\n }\n};\n```\n# Python Code\n```\nclass Solution:\n def countOrders(self, n: int) -> int:\n mod=10**9+7\n num=1\n for i in range(1, n):\n num=num*(i+1)*(2*i+1)%mod\n return num\n```\n# Python 1 line\n```\nclass Solution:\n def countOrders(self, n: int) -> int:\n return factorial(2*n)//(2**n)%(10**9+7)\n``` | 10 | Given `n` orders, each order consist in pickup and delivery services.
Count all valid pickup/delivery possible sequences such that delivery(i) is always after of pickup(i).
Since the answer may be too large, return it modulo 10^9 + 7.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation:** Unique order (P1, D1), Delivery 1 always is after of Pickup 1.
**Example 2:**
**Input:** n = 2
**Output:** 6
**Explanation:** All possible orders:
(P1,P2,D1,D2), (P1,P2,D2,D1), (P1,D1,P2,D2), (P2,P1,D1,D2), (P2,P1,D2,D1) and (P2,D2,P1,D1).
This is an invalid order (P1,D2,P2,D1) because Pickup 2 is after of Delivery 2.
**Example 3:**
**Input:** n = 3
**Output:** 90
**Constraints:**
* `1 <= n <= 500`
Given 2 integers n and start. Your task is return any permutation p of (0,1,2.....,2^n -1) such that : p\[0\] = start, p\[i\] and p\[i+1\] differ by only one bit for all 0 <= i < 2^n - 1. | Use gray code to generate a n-bit sequence. Rotate the sequence such that its first element is start. |
C++/Python Math recursion->1 loop->1 line | count-all-valid-pickup-and-delivery-options | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is a permutation problem.\n$$\nF(n)=\\frac{(2n)!}{2^n}\n$$\nUse the recurrence\n$$\nF(n+1)=F(n)\\times(n+1)\\times (2n+1)\n$$\n# Approach\n<!-- Describe your approach to solving the problem. -->\n[Please turn on English subtitles if necessary]\n[https://youtu.be/erH5HQf24J4?si=nG8Pde5LRuwpI8hF](https://youtu.be/erH5HQf24J4?si=nG8Pde5LRuwpI8hF)\nThere are (2n) objects to arrange in a list.\nSo there are (2n)! ways to permute without any constraints. Consider the following 2 sequences\n```\n****************Pi*********Di**********\n****************Di*********Pi**********\n```\nwhere both are identical except for Pi & Di.\nBut every pair $(P_i, D_i)$ must be in this order. So 1/2 of them follow this order. There are n pairs. So the number for valid sequences is\n$$\nF(n)=\\frac{(2n)!}{2^n}\n$$\n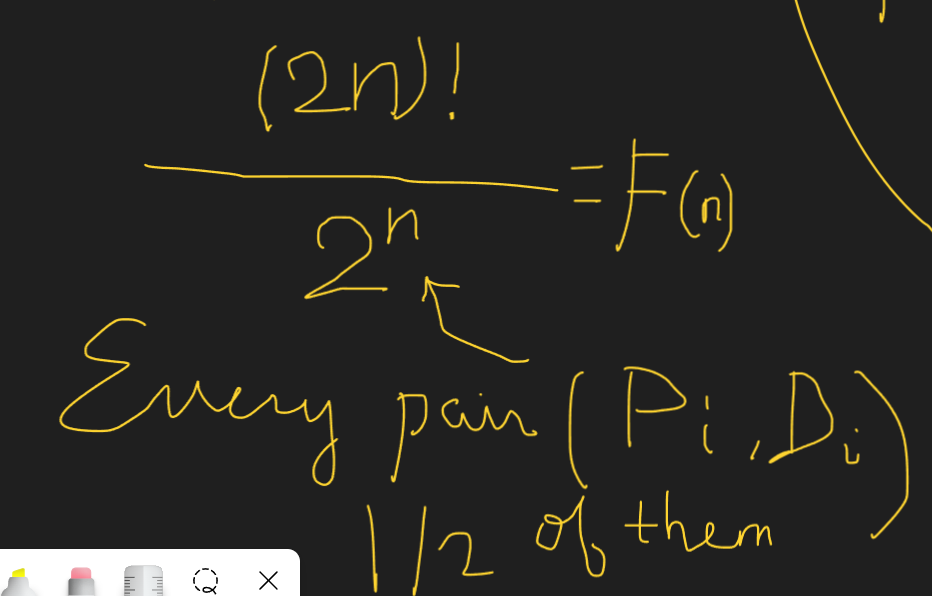\n# How Recursion?\nOne way is to compare $F(n)$ & $F(n+1)$ using $\nF(n)=\\frac{(2n)!}{2^n}\n$.\nThere is still other way using combination.\nOne wants to place the pair $(P_{n+1}, D_{n+1})$ in $(2n+2)$ positions. There are \n$$\nC^{2n+2}_2=(n+1)\\times (2n+1)\n$$\nways for placing this pair. Using multiplication principle for counting, the rest is arranging $(P_i, D_i) \\ (i=1,\\dots n) $ with number $F(n)$. So one has\n$$\nF(n+1)=F(n)\\times(n+1)\\times (2n+1)\n$$\nwith the initial case $F(1)=1$.\n\n# 1 line solution\n[https://youtu.be/enZbhnVRuLk?si=E_NanOduoKKMN7u1](https://youtu.be/enZbhnVRuLk?si=E_NanOduoKKMN7u1)\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code\n```\nclass Solution {\npublic:\n const int mod=1e9+7;\n int countOrders(int n) {\n long long num=1;\n for(long long i=1; i<n; i++){\n num=(num*(i+1)*(2*i+1)%mod);\n }\n return num;\n }\n};\n```\n# Python Code\n```\nclass Solution:\n def countOrders(self, n: int) -> int:\n mod=10**9+7\n num=1\n for i in range(1, n):\n num=num*(i+1)*(2*i+1)%mod\n return num\n```\n# Python 1 line\n```\nclass Solution:\n def countOrders(self, n: int) -> int:\n return factorial(2*n)//(2**n)%(10**9+7)\n``` | 10 | Given a binary string `s` and an integer `k`, return `true` _if every binary code of length_ `k` _is a substring of_ `s`. Otherwise, return `false`.
**Example 1:**
**Input:** s = "00110110 ", k = 2
**Output:** true
**Explanation:** The binary codes of length 2 are "00 ", "01 ", "10 " and "11 ". They can be all found as substrings at indices 0, 1, 3 and 2 respectively.
**Example 2:**
**Input:** s = "0110 ", k = 1
**Output:** true
**Explanation:** The binary codes of length 1 are "0 " and "1 ", it is clear that both exist as a substring.
**Example 3:**
**Input:** s = "0110 ", k = 2
**Output:** false
**Explanation:** The binary code "00 " is of length 2 and does not exist in the array.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= k <= 20` | Use the permutation and combination theory to add one (P, D) pair each time until n pairs. |
✔96.89% Beats C++😍||Hard-->Easy✨|| Easy to understand 📈🧠|| With commented code 😇|| #Beginner😉😎 | count-all-valid-pickup-and-delivery-options | 1 | 1 | # Problem Understanding:\n\n- The problem is asking us to count the number of valid orders in which \'n\' items can be arranged. \n- Each item takes up two places, and we want to find the total number of valid sequences for these items.\n\n# Strategies to Tackle the Problem:\n\n**Initialize Variables:**\n\n- Initialize two variables, `places` and `seq`, to keep track of the number of places available and the total sequence count, respectively.\n- Initialize a constant `MOD` for modulo arithmetic.\n\n**Loop from \'n\' down to 1:**\n\n- We start a loop from \'n\' down to 1 to calculate the sequence count for each item.\n\n **Calculate Sequence Count for the Current Item:**\n\n- Within the loop, we calculate the sequence count for the current item using a formula:\n- `seq = (seq * ((places * (places - 1)) / 2)) % MOD`\n- This formula calculates the number of valid sequences for the current item.\n- It assumes that you can choose any of the remaining 2 * n places for the current item and any of the remaining 2 * n - 1 places for the next item.\n- We divide by 2 to account for double-counting.\n\n **Decrement Places for the Next Iteration:**\n\n- After calculating the sequence count for the current item, decrement the number of available places by 2 for the next iteration.\n\n\n**Return the Final Sequence Count:**\n\n- After the loop is finished, return the final sequence count as an integer (modulo MOD).\n\n\n# Intuition\n- The problem involves finding the number of valid sequences for arranging \'n\' items, where each item occupies two spots, and you want to count the total valid orders. \n- The approach involves iteratively calculating the number of valid sequences for each item and updating the count.\n\n# Approach\n1. **Initialize Variables:**\n\n- Initialize two variables: `places` and `seq`.\n- `places` represents the total number of available places for arranging items and starts at 2 * n because each item takes two spots.\n- `seq` is the sequence count and starts at 1 since there is only one way to arrange the items initially.\n\n1. **Iterate from n down to 1:**\n\n- Start a loop from \'n\' down to 1. This loop will calculate the sequence count for each item.\n\n1. **Calculate Sequence Count for Current Item:**\n\n- Within the loop, use the following formula to calculate the sequence count for the current item:\n```\nseq = (seq * ((places * (places - 1)) / 2)) % MOD\n\n```\n- Multiply the current sequence count `seq` by `(places * (places - 1)) / 2`. This formula represents the number of valid sequences for the current item.\n- It assumes that you can choose any of the remaining 2 * n places for the current item and any of the remaining 2 * n - 1 places for the next item.\n- Divide by 2 to account for double-counting.\n\n**Update Available Places for Next Iteration:**\n\n- After calculating the sequence count for the current item, decrement the number of available places (`places`) by 2. This accounts for the fact that each item occupies two spots.\n- \n **Return the Final Sequence Count:**\n\n- After completing the loop for all \'n\' items, return the final sequence count (`seq`) as an integer (modulo `MOD`).\n\n# Overall Idea:\n\n- You are gradually building the sequence count by considering each item one by one.\n- The formula inside the loop efficiently calculates the valid sequences for each item, and you multiply it with the current sequence count.\n- By updating the available places and using modulo arithmetic, you ensure that the result remains within bounds.\n\n\n- This approach efficiently solves the problem of counting valid orders for arranging \'n\' items in a way that is easy to understand and implement.\n# Complexity\n**- Time complexity:**\n- **The main loop in the code runs from \'n\' down to 1**. Therefore, the `time complexity of this code is O(n)`.\n\n**- Space complexity:**\n- `The space complexity of the given code is O(1)`, which means that the memory used by the code is constant and does not depend on the size of the input \'n\'. \n- **This is because the code only uses a fixed number of variables** and constants regardless of the value of \'n\'.\n\n# PLEASE UPVOTE\u2763\uD83D\uDE0D\n\n# Code\n```\nclass Solution {\npublic:\n // Define a constant MOD to be used for modulo arithmetic\n int MOD = 1e9 + 7;\n\n // Function to count valid orders\n int countOrders(int n) {\n // Initialize variables to store the number of places and the total sequence count\n long places = 2 * n; // There are 2 places for each item\n long seq = 1; // Initialize the sequence count to 1\n\n // Loop from n down to 1\n for (int i = n; i >= 1; i--) {\n // Calculate the sequence count for the current item\n // The formula below calculates the number of valid sequences for the current item\n // by multiplying the current sequence count by (places * (places - 1)) / 2\n // This formula assumes that you can choose any of the remaining 2 * n places\n // for the current item, and then any of the remaining 2 * n - 1 places for the next item,\n // divided by 2 to account for double-counting.\n seq = (seq * ((places * (places - 1)) / 2)) % MOD;\n\n // Decrement the number of available places by 2 for the next iteration\n places = places - 2;\n }\n \n // Return the final sequence count as an integer (modulo MOD)\n return (int)seq;\n }\n};\n\n```\n# JAVA\n```\npublic class Solution {\n // Define a constant MOD to be used for modulo arithmetic\n private static final int MOD = 1000000007;\n\n // Function to count valid orders\n public int countOrders(int n) {\n // Initialize variables to store the number of places and the total sequence count\n long places = 2 * n; // There are 2 places for each item\n long seq = 1; // Initialize the sequence count to 1\n\n // Loop from n down to 1\n for (int i = n; i >= 1; i--) {\n // Calculate the sequence count for the current item\n // The formula below calculates the number of valid sequences for the current item\n // by multiplying the current sequence count by (places * (places - 1)) / 2\n // This formula assumes that you can choose any of the remaining 2 * n places\n // for the current item, and then any of the remaining 2 * n - 1 places for the next item,\n // divided by 2 to account for double-counting.\n seq = (seq * ((places * (places - 1)) / 2)) % MOD;\n\n // Decrement the number of available places by 2 for the next iteration\n places = places - 2;\n }\n\n // Return the final sequence count as an integer (modulo MOD)\n return (int)seq;\n }\n}\n\n```\n# JAVASRIPT\n```\nclass Solution {\n // Define a constant MOD to be used for modulo arithmetic\n static MOD = 1000000007;\n\n // Function to count valid orders\n countOrders(n) {\n // Initialize variables to store the number of places and the total sequence count\n let places = 2 * n; // There are 2 places for each item\n let seq = 1; // Initialize the sequence count to 1\n\n // Loop from n down to 1\n for (let i = n; i >= 1; i--) {\n // Calculate the sequence count for the current item\n // The formula below calculates the number of valid sequences for the current item\n // by multiplying the current sequence count by (places * (places - 1)) / 2\n // This formula assumes that you can choose any of the remaining 2 * n places\n // for the current item, and then any of the remaining 2 * n - 1 places for the next item,\n // divided by 2 to account for double-counting.\n seq = (seq * ((places * (places - 1)) / 2)) % Solution.MOD;\n\n // Decrement the number of available places by 2 for the next iteration\n places = places - 2;\n }\n\n // Return the final sequence count as an integer (modulo MOD)\n return Math.floor(seq);\n }\n}\n\n// Example usage:\nconst solution = new Solution();\nconst result = solution.countOrders(3); // You can replace 3 with any desired value of \'n\'\nconsole.log(result);\n\n```\n# PYTHON\n```\nclass Solution:\n # Define a constant MOD to be used for modulo arithmetic\n MOD = 1000000007\n\n # Function to count valid orders\n def countOrders(self, n: int) -> int:\n # Initialize variables to store the number of places and the total sequence count\n places = 2 * n # There are 2 places for each item\n seq = 1 # Initialize the sequence count to 1\n\n # Loop from n down to 1\n for i in range(n, 0, -1):\n # Calculate the sequence count for the current item\n # The formula below calculates the number of valid sequences for the current item\n # by multiplying the current sequence count by (places * (places - 1)) / 2\n # This formula assumes that you can choose any of the remaining 2 * n places\n # for the current item, and then any of the remaining 2 * n - 1 places for the next item,\n # divided by 2 to account for double-counting.\n seq = (seq * ((places * (places - 1)) // 2)) % Solution.MOD\n\n # Decrement the number of available places by 2 for the next iteration\n places = places - 2\n\n # Return the final sequence count as an integer (modulo MOD)\n return int(seq)\n\n# Example usage:\nsolution = Solution()\nresult = solution.countOrders(3) # You can replace 3 with any desired value of \'n\'\nprint(result)\n\n\n```\n# GO\n```\npackage main\n\nimport (\n\t"math"\n)\n\n// Solution represents the solution class\ntype Solution struct {\n\tMOD int\n}\n\n// NewSolution initializes a new Solution instance\nfunc NewSolution() Solution {\n\treturn Solution{MOD: 1000000007}\n}\n\n// CountOrders counts the valid orders\nfunc (s *Solution) CountOrders(n int) int {\n\t// Initialize variables to store the number of places and the total sequence count\n\tplaces := 2 * n // There are 2 places for each item\n\tseq := int64(1) // Initialize the sequence count to 1\n\n\t// Loop from n down to 1\n\tfor i := n; i >= 1; i-- {\n\t\t// Calculate the sequence count for the current item\n\t\t// The formula below calculates the number of valid sequences for the current item\n\t\t// by multiplying the current sequence count by (places * (places - 1)) / 2\n\t\t// This formula assumes that you can choose any of the remaining 2 * n places\n\t\t// for the current item, and then any of the remaining 2 * n - 1 places for the next item,\n\t\t// divided by 2 to account for double-counting.\n\t\tseq = (seq * int64((places * (places - 1)) / 2)) % int64(s.MOD)\n\n\t\t// Decrement the number of available places by 2 for the next iteration\n\t\tplaces = places - 2\n\t}\n\n\t// Return the final sequence count as an integer (modulo MOD)\n\treturn int(seq)\n}\n\nfunc main() {\n\t// Example usage:\n\tsolution := NewSolution()\n\tresult := solution.CountOrders(3) // You can replace 3 with any desired value of \'n\'\n\tprintln(result)\n}\n\n```\n# PLEASE UPVOTE\u2763\uD83D\uDE0D | 5 | Given `n` orders, each order consist in pickup and delivery services.
Count all valid pickup/delivery possible sequences such that delivery(i) is always after of pickup(i).
Since the answer may be too large, return it modulo 10^9 + 7.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation:** Unique order (P1, D1), Delivery 1 always is after of Pickup 1.
**Example 2:**
**Input:** n = 2
**Output:** 6
**Explanation:** All possible orders:
(P1,P2,D1,D2), (P1,P2,D2,D1), (P1,D1,P2,D2), (P2,P1,D1,D2), (P2,P1,D2,D1) and (P2,D2,P1,D1).
This is an invalid order (P1,D2,P2,D1) because Pickup 2 is after of Delivery 2.
**Example 3:**
**Input:** n = 3
**Output:** 90
**Constraints:**
* `1 <= n <= 500`
Given 2 integers n and start. Your task is return any permutation p of (0,1,2.....,2^n -1) such that : p\[0\] = start, p\[i\] and p\[i+1\] differ by only one bit for all 0 <= i < 2^n - 1. | Use gray code to generate a n-bit sequence. Rotate the sequence such that its first element is start. |
✔96.89% Beats C++😍||Hard-->Easy✨|| Easy to understand 📈🧠|| With commented code 😇|| #Beginner😉😎 | count-all-valid-pickup-and-delivery-options | 1 | 1 | # Problem Understanding:\n\n- The problem is asking us to count the number of valid orders in which \'n\' items can be arranged. \n- Each item takes up two places, and we want to find the total number of valid sequences for these items.\n\n# Strategies to Tackle the Problem:\n\n**Initialize Variables:**\n\n- Initialize two variables, `places` and `seq`, to keep track of the number of places available and the total sequence count, respectively.\n- Initialize a constant `MOD` for modulo arithmetic.\n\n**Loop from \'n\' down to 1:**\n\n- We start a loop from \'n\' down to 1 to calculate the sequence count for each item.\n\n **Calculate Sequence Count for the Current Item:**\n\n- Within the loop, we calculate the sequence count for the current item using a formula:\n- `seq = (seq * ((places * (places - 1)) / 2)) % MOD`\n- This formula calculates the number of valid sequences for the current item.\n- It assumes that you can choose any of the remaining 2 * n places for the current item and any of the remaining 2 * n - 1 places for the next item.\n- We divide by 2 to account for double-counting.\n\n **Decrement Places for the Next Iteration:**\n\n- After calculating the sequence count for the current item, decrement the number of available places by 2 for the next iteration.\n\n\n**Return the Final Sequence Count:**\n\n- After the loop is finished, return the final sequence count as an integer (modulo MOD).\n\n\n# Intuition\n- The problem involves finding the number of valid sequences for arranging \'n\' items, where each item occupies two spots, and you want to count the total valid orders. \n- The approach involves iteratively calculating the number of valid sequences for each item and updating the count.\n\n# Approach\n1. **Initialize Variables:**\n\n- Initialize two variables: `places` and `seq`.\n- `places` represents the total number of available places for arranging items and starts at 2 * n because each item takes two spots.\n- `seq` is the sequence count and starts at 1 since there is only one way to arrange the items initially.\n\n1. **Iterate from n down to 1:**\n\n- Start a loop from \'n\' down to 1. This loop will calculate the sequence count for each item.\n\n1. **Calculate Sequence Count for Current Item:**\n\n- Within the loop, use the following formula to calculate the sequence count for the current item:\n```\nseq = (seq * ((places * (places - 1)) / 2)) % MOD\n\n```\n- Multiply the current sequence count `seq` by `(places * (places - 1)) / 2`. This formula represents the number of valid sequences for the current item.\n- It assumes that you can choose any of the remaining 2 * n places for the current item and any of the remaining 2 * n - 1 places for the next item.\n- Divide by 2 to account for double-counting.\n\n**Update Available Places for Next Iteration:**\n\n- After calculating the sequence count for the current item, decrement the number of available places (`places`) by 2. This accounts for the fact that each item occupies two spots.\n- \n **Return the Final Sequence Count:**\n\n- After completing the loop for all \'n\' items, return the final sequence count (`seq`) as an integer (modulo `MOD`).\n\n# Overall Idea:\n\n- You are gradually building the sequence count by considering each item one by one.\n- The formula inside the loop efficiently calculates the valid sequences for each item, and you multiply it with the current sequence count.\n- By updating the available places and using modulo arithmetic, you ensure that the result remains within bounds.\n\n\n- This approach efficiently solves the problem of counting valid orders for arranging \'n\' items in a way that is easy to understand and implement.\n# Complexity\n**- Time complexity:**\n- **The main loop in the code runs from \'n\' down to 1**. Therefore, the `time complexity of this code is O(n)`.\n\n**- Space complexity:**\n- `The space complexity of the given code is O(1)`, which means that the memory used by the code is constant and does not depend on the size of the input \'n\'. \n- **This is because the code only uses a fixed number of variables** and constants regardless of the value of \'n\'.\n\n# PLEASE UPVOTE\u2763\uD83D\uDE0D\n\n# Code\n```\nclass Solution {\npublic:\n // Define a constant MOD to be used for modulo arithmetic\n int MOD = 1e9 + 7;\n\n // Function to count valid orders\n int countOrders(int n) {\n // Initialize variables to store the number of places and the total sequence count\n long places = 2 * n; // There are 2 places for each item\n long seq = 1; // Initialize the sequence count to 1\n\n // Loop from n down to 1\n for (int i = n; i >= 1; i--) {\n // Calculate the sequence count for the current item\n // The formula below calculates the number of valid sequences for the current item\n // by multiplying the current sequence count by (places * (places - 1)) / 2\n // This formula assumes that you can choose any of the remaining 2 * n places\n // for the current item, and then any of the remaining 2 * n - 1 places for the next item,\n // divided by 2 to account for double-counting.\n seq = (seq * ((places * (places - 1)) / 2)) % MOD;\n\n // Decrement the number of available places by 2 for the next iteration\n places = places - 2;\n }\n \n // Return the final sequence count as an integer (modulo MOD)\n return (int)seq;\n }\n};\n\n```\n# JAVA\n```\npublic class Solution {\n // Define a constant MOD to be used for modulo arithmetic\n private static final int MOD = 1000000007;\n\n // Function to count valid orders\n public int countOrders(int n) {\n // Initialize variables to store the number of places and the total sequence count\n long places = 2 * n; // There are 2 places for each item\n long seq = 1; // Initialize the sequence count to 1\n\n // Loop from n down to 1\n for (int i = n; i >= 1; i--) {\n // Calculate the sequence count for the current item\n // The formula below calculates the number of valid sequences for the current item\n // by multiplying the current sequence count by (places * (places - 1)) / 2\n // This formula assumes that you can choose any of the remaining 2 * n places\n // for the current item, and then any of the remaining 2 * n - 1 places for the next item,\n // divided by 2 to account for double-counting.\n seq = (seq * ((places * (places - 1)) / 2)) % MOD;\n\n // Decrement the number of available places by 2 for the next iteration\n places = places - 2;\n }\n\n // Return the final sequence count as an integer (modulo MOD)\n return (int)seq;\n }\n}\n\n```\n# JAVASRIPT\n```\nclass Solution {\n // Define a constant MOD to be used for modulo arithmetic\n static MOD = 1000000007;\n\n // Function to count valid orders\n countOrders(n) {\n // Initialize variables to store the number of places and the total sequence count\n let places = 2 * n; // There are 2 places for each item\n let seq = 1; // Initialize the sequence count to 1\n\n // Loop from n down to 1\n for (let i = n; i >= 1; i--) {\n // Calculate the sequence count for the current item\n // The formula below calculates the number of valid sequences for the current item\n // by multiplying the current sequence count by (places * (places - 1)) / 2\n // This formula assumes that you can choose any of the remaining 2 * n places\n // for the current item, and then any of the remaining 2 * n - 1 places for the next item,\n // divided by 2 to account for double-counting.\n seq = (seq * ((places * (places - 1)) / 2)) % Solution.MOD;\n\n // Decrement the number of available places by 2 for the next iteration\n places = places - 2;\n }\n\n // Return the final sequence count as an integer (modulo MOD)\n return Math.floor(seq);\n }\n}\n\n// Example usage:\nconst solution = new Solution();\nconst result = solution.countOrders(3); // You can replace 3 with any desired value of \'n\'\nconsole.log(result);\n\n```\n# PYTHON\n```\nclass Solution:\n # Define a constant MOD to be used for modulo arithmetic\n MOD = 1000000007\n\n # Function to count valid orders\n def countOrders(self, n: int) -> int:\n # Initialize variables to store the number of places and the total sequence count\n places = 2 * n # There are 2 places for each item\n seq = 1 # Initialize the sequence count to 1\n\n # Loop from n down to 1\n for i in range(n, 0, -1):\n # Calculate the sequence count for the current item\n # The formula below calculates the number of valid sequences for the current item\n # by multiplying the current sequence count by (places * (places - 1)) / 2\n # This formula assumes that you can choose any of the remaining 2 * n places\n # for the current item, and then any of the remaining 2 * n - 1 places for the next item,\n # divided by 2 to account for double-counting.\n seq = (seq * ((places * (places - 1)) // 2)) % Solution.MOD\n\n # Decrement the number of available places by 2 for the next iteration\n places = places - 2\n\n # Return the final sequence count as an integer (modulo MOD)\n return int(seq)\n\n# Example usage:\nsolution = Solution()\nresult = solution.countOrders(3) # You can replace 3 with any desired value of \'n\'\nprint(result)\n\n\n```\n# GO\n```\npackage main\n\nimport (\n\t"math"\n)\n\n// Solution represents the solution class\ntype Solution struct {\n\tMOD int\n}\n\n// NewSolution initializes a new Solution instance\nfunc NewSolution() Solution {\n\treturn Solution{MOD: 1000000007}\n}\n\n// CountOrders counts the valid orders\nfunc (s *Solution) CountOrders(n int) int {\n\t// Initialize variables to store the number of places and the total sequence count\n\tplaces := 2 * n // There are 2 places for each item\n\tseq := int64(1) // Initialize the sequence count to 1\n\n\t// Loop from n down to 1\n\tfor i := n; i >= 1; i-- {\n\t\t// Calculate the sequence count for the current item\n\t\t// The formula below calculates the number of valid sequences for the current item\n\t\t// by multiplying the current sequence count by (places * (places - 1)) / 2\n\t\t// This formula assumes that you can choose any of the remaining 2 * n places\n\t\t// for the current item, and then any of the remaining 2 * n - 1 places for the next item,\n\t\t// divided by 2 to account for double-counting.\n\t\tseq = (seq * int64((places * (places - 1)) / 2)) % int64(s.MOD)\n\n\t\t// Decrement the number of available places by 2 for the next iteration\n\t\tplaces = places - 2\n\t}\n\n\t// Return the final sequence count as an integer (modulo MOD)\n\treturn int(seq)\n}\n\nfunc main() {\n\t// Example usage:\n\tsolution := NewSolution()\n\tresult := solution.CountOrders(3) // You can replace 3 with any desired value of \'n\'\n\tprintln(result)\n}\n\n```\n# PLEASE UPVOTE\u2763\uD83D\uDE0D | 5 | Given a binary string `s` and an integer `k`, return `true` _if every binary code of length_ `k` _is a substring of_ `s`. Otherwise, return `false`.
**Example 1:**
**Input:** s = "00110110 ", k = 2
**Output:** true
**Explanation:** The binary codes of length 2 are "00 ", "01 ", "10 " and "11 ". They can be all found as substrings at indices 0, 1, 3 and 2 respectively.
**Example 2:**
**Input:** s = "0110 ", k = 1
**Output:** true
**Explanation:** The binary codes of length 1 are "0 " and "1 ", it is clear that both exist as a substring.
**Example 3:**
**Input:** s = "0110 ", k = 2
**Output:** false
**Explanation:** The binary code "00 " is of length 2 and does not exist in the array.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= k <= 20` | Use the permutation and combination theory to add one (P, D) pair each time until n pairs. |
Python | Easy to Understand | Fast | Optimal Solution | count-all-valid-pickup-and-delivery-options | 0 | 1 | # Python | Easy to Understand | Fast | Optimal Solution\n```\nfrom functools import reduce\nfrom operator import mul\nclass Solution:\n def countOrders(self, n: int) -> int:\n return reduce(mul, (*range(1,n+1), *range(1,2*n,2)), 1) % (10**9+7)\n``` | 13 | Given `n` orders, each order consist in pickup and delivery services.
Count all valid pickup/delivery possible sequences such that delivery(i) is always after of pickup(i).
Since the answer may be too large, return it modulo 10^9 + 7.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation:** Unique order (P1, D1), Delivery 1 always is after of Pickup 1.
**Example 2:**
**Input:** n = 2
**Output:** 6
**Explanation:** All possible orders:
(P1,P2,D1,D2), (P1,P2,D2,D1), (P1,D1,P2,D2), (P2,P1,D1,D2), (P2,P1,D2,D1) and (P2,D2,P1,D1).
This is an invalid order (P1,D2,P2,D1) because Pickup 2 is after of Delivery 2.
**Example 3:**
**Input:** n = 3
**Output:** 90
**Constraints:**
* `1 <= n <= 500`
Given 2 integers n and start. Your task is return any permutation p of (0,1,2.....,2^n -1) such that : p\[0\] = start, p\[i\] and p\[i+1\] differ by only one bit for all 0 <= i < 2^n - 1. | Use gray code to generate a n-bit sequence. Rotate the sequence such that its first element is start. |
Python | Easy to Understand | Fast | Optimal Solution | count-all-valid-pickup-and-delivery-options | 0 | 1 | # Python | Easy to Understand | Fast | Optimal Solution\n```\nfrom functools import reduce\nfrom operator import mul\nclass Solution:\n def countOrders(self, n: int) -> int:\n return reduce(mul, (*range(1,n+1), *range(1,2*n,2)), 1) % (10**9+7)\n``` | 13 | Given a binary string `s` and an integer `k`, return `true` _if every binary code of length_ `k` _is a substring of_ `s`. Otherwise, return `false`.
**Example 1:**
**Input:** s = "00110110 ", k = 2
**Output:** true
**Explanation:** The binary codes of length 2 are "00 ", "01 ", "10 " and "11 ". They can be all found as substrings at indices 0, 1, 3 and 2 respectively.
**Example 2:**
**Input:** s = "0110 ", k = 1
**Output:** true
**Explanation:** The binary codes of length 1 are "0 " and "1 ", it is clear that both exist as a substring.
**Example 3:**
**Input:** s = "0110 ", k = 2
**Output:** false
**Explanation:** The binary code "00 " is of length 2 and does not exist in the array.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= k <= 20` | Use the permutation and combination theory to add one (P, D) pair each time until n pairs. |
Python Simple Solution with time complexity O(n) | count-all-valid-pickup-and-delivery-options | 0 | 1 | # Intuition\n\nWe have n orders means total 2n options,out of 2n places1st place is always placeorder and further places could be place order or delivered, last place will always be delivered.\n\n- The intuition behind this code is to calculate the total number of valid orderings of n different products in 2n available spaces. \n\n- It does this by iteratively multiplying res by x and m, effectively calculating the permutations of products in available spaces.\n\n- The modulus operation is applied to the result to keep it within a manageable range. This code essentially computes the number of valid orderings using a mathematical formula based on combinatorics.\n\n# Approach\n\n##Example 1: for n=10 -->\n>we have 10 option for 1st place and then (10-1)+10 for next place same follow till n not equals to one.\n\n\n>n decreases by one and for each n next place would be 2n-1\n\n10x19x9x17x8x15x7x13x6x11x5x9x4x7x3x5x2x3x1x1\n \nreturn it with mudolo 10^9+7 \n\n\n\n##Example 2: for n=5 -->\n>we have 5 option for 1st place and then (5-1)+5 for next place same follow till n not equals to one.\n\n\n>n decreases by one and for each n next place would be 2n-1\n\n5x9x4x7x3x5x2x3x1x1\n \nreturn it with mudolo 10^9+7 \n\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def countOrders(self, n: int) -> int:\n mod=10**9+7\n x=n\n m=2*n-1\n res=1\n for i in range(2*n):\n if x!=0 and m!=0:\n res*=x\n res*=m\n x-=1\n m-=2\n return res%mod\n\n``` | 3 | Given `n` orders, each order consist in pickup and delivery services.
Count all valid pickup/delivery possible sequences such that delivery(i) is always after of pickup(i).
Since the answer may be too large, return it modulo 10^9 + 7.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation:** Unique order (P1, D1), Delivery 1 always is after of Pickup 1.
**Example 2:**
**Input:** n = 2
**Output:** 6
**Explanation:** All possible orders:
(P1,P2,D1,D2), (P1,P2,D2,D1), (P1,D1,P2,D2), (P2,P1,D1,D2), (P2,P1,D2,D1) and (P2,D2,P1,D1).
This is an invalid order (P1,D2,P2,D1) because Pickup 2 is after of Delivery 2.
**Example 3:**
**Input:** n = 3
**Output:** 90
**Constraints:**
* `1 <= n <= 500`
Given 2 integers n and start. Your task is return any permutation p of (0,1,2.....,2^n -1) such that : p\[0\] = start, p\[i\] and p\[i+1\] differ by only one bit for all 0 <= i < 2^n - 1. | Use gray code to generate a n-bit sequence. Rotate the sequence such that its first element is start. |
Python Simple Solution with time complexity O(n) | count-all-valid-pickup-and-delivery-options | 0 | 1 | # Intuition\n\nWe have n orders means total 2n options,out of 2n places1st place is always placeorder and further places could be place order or delivered, last place will always be delivered.\n\n- The intuition behind this code is to calculate the total number of valid orderings of n different products in 2n available spaces. \n\n- It does this by iteratively multiplying res by x and m, effectively calculating the permutations of products in available spaces.\n\n- The modulus operation is applied to the result to keep it within a manageable range. This code essentially computes the number of valid orderings using a mathematical formula based on combinatorics.\n\n# Approach\n\n##Example 1: for n=10 -->\n>we have 10 option for 1st place and then (10-1)+10 for next place same follow till n not equals to one.\n\n\n>n decreases by one and for each n next place would be 2n-1\n\n10x19x9x17x8x15x7x13x6x11x5x9x4x7x3x5x2x3x1x1\n \nreturn it with mudolo 10^9+7 \n\n\n\n##Example 2: for n=5 -->\n>we have 5 option for 1st place and then (5-1)+5 for next place same follow till n not equals to one.\n\n\n>n decreases by one and for each n next place would be 2n-1\n\n5x9x4x7x3x5x2x3x1x1\n \nreturn it with mudolo 10^9+7 \n\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def countOrders(self, n: int) -> int:\n mod=10**9+7\n x=n\n m=2*n-1\n res=1\n for i in range(2*n):\n if x!=0 and m!=0:\n res*=x\n res*=m\n x-=1\n m-=2\n return res%mod\n\n``` | 3 | Given a binary string `s` and an integer `k`, return `true` _if every binary code of length_ `k` _is a substring of_ `s`. Otherwise, return `false`.
**Example 1:**
**Input:** s = "00110110 ", k = 2
**Output:** true
**Explanation:** The binary codes of length 2 are "00 ", "01 ", "10 " and "11 ". They can be all found as substrings at indices 0, 1, 3 and 2 respectively.
**Example 2:**
**Input:** s = "0110 ", k = 1
**Output:** true
**Explanation:** The binary codes of length 1 are "0 " and "1 ", it is clear that both exist as a substring.
**Example 3:**
**Input:** s = "0110 ", k = 2
**Output:** false
**Explanation:** The binary code "00 " is of length 2 and does not exist in the array.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= k <= 20` | Use the permutation and combination theory to add one (P, D) pair each time until n pairs. |
✅ 99.57% DP & Math & Recursion | count-all-valid-pickup-and-delivery-options | 1 | 1 | # Comprehensive Guide to Solving "Count All Valid Pickup and Delivery Options": Dynamic Programming, Recursion, and Math Approaches\n\n## Introduction & Problem Statement\n\nGreetings, aspiring problem solvers! Today we\'ll unravel an intriguing combinatorial problem that revolves around orders, pickups, and deliveries\u2014aptly named **Count All Valid Pickup and Delivery Options**. The problem hands you `n` orders, each consisting of a pickup and delivery service. Your goal is to figure out the number of valid pickup and delivery sequences such that the delivery of each order `i` occurs after its corresponding pickup.\n\n## Key Concepts and Constraints\n\n### What Makes this Problem Unique?\n\n1. **Pairing**: \n Each order contains a pair of services: a pickup (P) and a delivery (D). For order `i`, the pickup is denoted as `P_i` and the delivery as `D_i`.\n \n2. **Order Matters**: \n The sequences are sensitive to the order. `(P1, D1, P2, D2)` is considered different from `(P2, D2, P1, D1)`.\n\n3. **Constraints**: \n - `n` ranges between 1 and 500.\n\n---\n\n# Strategies to Tackle the Problem: A Three-Pronged Approach\n\n## Live Coding 3-in-1 & Explaining\nhttps://youtu.be/wj3vBARk8-U?si=_gFWsftHvd3o_zYN\n\n## Method 1: Dynamic Programming \n\n## What is Dynamic Programming (DP)?\n\nThink of Dynamic Programming as a way to build a solution step-by-step, just like building a LEGO tower. You start with one block and then keep adding more to get the final shape. In a similar way, you start with a simple problem, solve it, and use that solution to solve more complex problems.\n\n## Detailed Steps\n\n### Step 1: Setting a Starting Point (Base Case)\n\n- **Why do we start with `count = 1`?** \n - Imagine you have just one order. This order has one pickup (P1) and one delivery (D1). The only rule is that the delivery (D1) must come after the pickup (P1). This gives you just one way to arrange this order: (P1, D1). So, you start your count at 1.\n\n### Step 2: Building Up the Solution (Iterative Computation)\n\n- **Why do we start the loop from 2?** \n - You\'ve already solved the problem for 1 order. Now you start adding more orders into the mix, one at a time, starting from the second order.\n\n- **What\'s the deal with `2i - 1` and `i`?** \n - Let\'s say you\'re at the `i-th` order. You would have `i` pickups and `i` deliveries, making it `2i` positions in total. \n - Now, when you\'re adding the pickup (Pi) for the `i-th` order, you can put it anywhere except at the end. That\'s `2i - 1` choices for Pi.\n - For Di, you only have `i` choices, because it must come after Pi.\n\n- **How do we update `count`?** \n - Multiply your current count by `(2i - 1) * i` to get the new count. This gives you the total number of sequences for `i` orders.\n\n### Step 3: The Final Answer\n\n- **How do you get the final answer?** \n - After you\'ve gone through all the orders, the value in `count` will be the total number of valid sequences. Return this value.\n\n## Time and Space Complexity\n\n- **Time Complexity**: The solution is speedy; it only takes linear time (`O(n)`).\n \n- **Space Complexity**: We don\'t use much extra space; just one variable (`count`). So the space complexity is `O(1)` or constant.\n\n## Clarification for the Formula `(2i - 1) * i`\n\n- **Why `(2i - 1) * i`?** \n - Think of it this way: for each new order, you have a "slot" for pickup and a "slot" for delivery. The pickup can go in `2i - 1` places, and the delivery in `i` places. You can think of these as dimensions: `2i - 1` for the width and `i` for the height. The total area or number of possibilities is the width multiplied by the height, which is `(2i - 1) * i`.\n\n# Code Dynamic Programming\n``` Python []\nMOD = 10**9 + 7\nclass Solution:\n def countOrders(self, n: int) -> int:\n count = 1 \n for i in range(2, n + 1):\n count = (count * (2 * i - 1) * i) % MOD\n return count\n```\n``` Go []\nconst MOD = 1000000007\n\nfunc countOrders(n int) int {\n count := 1\n for i := 2; i <= n; i++ {\n count = (count * (2 * i - 1) * i) % MOD\n }\n return count\n}\n```\n``` Rust []\nimpl Solution {\n const MOD: i64 = 1_000_000_007;\n \n pub fn count_orders(n: i32) -> i32 {\n let mut count: i64 = 1;\n for i in 2..=n {\n count = (count * ((2 * i - 1) as i64) * (i as i64)) % Self::MOD;\n }\n count as i32\n }\n}\n```\n``` C++ []\nclass Solution {\nconst int MOD = 1e9 + 7;\npublic:\n int countOrders(int n) {\n long long count = 1;\n for (int i = 2; i <= n; ++i) {\n count = (count * (2 * i - 1) * i) % MOD;\n }\n return (int)count;\n }\n};\n```\n``` Java []\npublic class Solution {\n private static final int MOD = 1000000007;\n\n public int countOrders(int n) {\n long count = 1;\n for (int i = 2; i <= n; i++) {\n count = (count * (2 * i - 1) * i) % MOD;\n }\n return (int) count;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} n\n * @return {number}\n */\nconst MOD = 1e9 + 7;\nvar countOrders = function(n) {\n let count = 1;\n for (let i = 2; i <= n; i++) {\n count = (count * (2 * i - 1) * i) % MOD;\n }\n return count;\n}\n```\n``` PHP []\nclass Solution {\n\n const MOD = 1000000007;\n\n /**\n * @param Integer $n\n * @return Integer\n */\n public function countOrders($n) {\n $count = 1;\n for ($i = 2; $i <= $n; $i++) {\n $count = ($count * (2 * $i - 1) * $i) % self::MOD;\n }\n return $count;\n }\n}\n```\n``` C# []\npublic class Solution {\n private const int MOD = 1000000007;\n\n public int CountOrders(int n) {\n long count = 1;\n for (int i = 2; i <= n; i++) {\n count = (count * (2 * i - 1) * i) % MOD;\n }\n return (int)count;\n }\n\n}\n```\n\n---\n\n## Method 2: Recursion with Memoization\n\n## The Sophistication of Memoization\n\nMemoization is an elegant technique that enhances the efficiency of recursive algorithms by storing the results of costly function calls. Imagine having a smart notebook that instantly provides answers to questions you\'ve already solved; that\'s what memoization does for your code.\n\n## A Comprehensive Step-by-Step Guide\n\n### Step 1: Create a Memoization Dictionary\n- **Why Use a Dictionary Called `memo`?** \n - The `memo` dictionary serves as a caching mechanism. It stores the number of valid sequences for a given `n` to avoid recalculating them repeatedly.\n\n### Step 2: Base Case\n- **Why Is the Base Case `n = 1`?** \n - When `n = 1`, there is only a single pair of pickup and delivery. There\'s just one way to sequence this pair\u2014by picking up first and then delivering. Hence, for `n = 1`, there is only one valid sequence.\n\n### Step 3: Recursive Calls Augmented with Memoization\n- **What Happens During the Recursive Calls?** \n - The function calls itself with `n - 1` as the argument.\n - Before diving deeper into recursion, it checks if the result for this `n` is already in `memo`. If so, it returns the stored result.\n - If not, it calculates the number of valid sequences for this `n` using the formula `count = countOrders(n - 1) * (2 * n - 1) * n` and then stores this result in `memo`.\n\n### Step 4: Return the Final Answer\n- **How Do We Get to the Final Answer?** \n - The `memo` dictionary will contain the number of valid sequences for the initial `n`. You simply return this value as the final result.\n\n## Time and Space Complexity Analysis\n\n- **Time Complexity**: `O(n)` \n Each unique value of `n` is calculated only once, and each calculation is done in constant time.\n \n- **Space Complexity**: `O(n)` \n The memoization dictionary stores up to `n` unique entries, making the space complexity linear.\n\n## Code Recursion with Memoization\n``` Python []\nMOD = 10**9 + 7 \nclass Solution:\n memo = {}\n def countOrders(self, n: int) -> int:\n if n == 1:\n return 1\n if n in self.memo:\n return self.memo[n]\n \n count = (self.countOrders(n - 1) * (2 * n - 1) * n) % MOD\n self.memo[n] = count\n return count\n```\n``` Go []\nconst MOD = 1000000007\n\nvar memo = map[int]int{}\n\nfunc countOrders(n int) int {\n\tif n == 1 {\n\t\treturn 1\n\t}\n\tif val, exists := memo[n]; exists {\n\t\treturn val\n\t}\n\n\tcount := (countOrders(n-1) * (2*n - 1) * n) % MOD\n\tmemo[n] = count\n\treturn count\n}\n```\n\n---\n\n## Method 3: The Mathematical Approach \n\n## The Majesty of Mathematics\n\nMathematics is like a teleportation device in the world of algorithms. It can directly take you to the solution, bypassing the need for iterative calculations or recursion.\n\n## A Thorough Step-by-Step Guide\n\n### Step 1: Calculating Factorial and Power\n- **Why Calculate `(2n)!` and `2^n`?** \n - The number of valid sequences can be directly derived using combinatorial mathematics. The formula involves `(2n)!` as well as `2^n`.\n\n### Step 2: Final Calculation and Return\n- **How Is the Final Result Calculated?** \n - The number of valid sequences is given by the formula `(2n)! / 2^n`. This can be calculated using modulo arithmetic to keep the numbers manageable.\n\n## Time and Space Complexity Analysis\n\n- **Time Complexity**: `O(n)` \n Calculating `(2n)!` involves `O(n)` operations.\n \n- **Space Complexity**: `O(1)` \n The space complexity is constant as we only use a few variables to store intermediate and final results.\n\n## Code Mathematical\n``` Python []\nMOD = 10**9 + 7 \nclass Solution:\n def countOrders(self, n: int) -> int:\n two_n_fact = factorial(2 * n) % MOD\n two_pow_n = pow(2, n, MOD)\n return (two_n_fact * pow(two_pow_n, -1, MOD)) % MOD\n```\n``` Go []\nconst MOD = 1000000007\n\nfunc factorial(n int) int {\n\tresult := 1\n\tfor i := 1; i <= n; i++ {\n\t\tresult = (result * i) % MOD\n\t}\n\treturn result\n}\n\nfunc pow(base, exp, mod int) int {\n\tresult := 1\n\tfor exp > 0 {\n\t\tif exp%2 == 1 {\n\t\t\tresult = (result * base) % mod\n\t\t}\n\t\tbase = (base * base) % mod\n\t\texp /= 2\n\t}\n\treturn result\n}\n\nfunc countOrders(n int) int {\n\ttwoNFact := factorial(2 * n) % MOD\n\ttwoPowN := pow(2, n, MOD)\n\treturn (twoNFact * pow(twoPowN, MOD-2, MOD)) % MOD\n}\n```\n\n## Performance\n\n| Language | Time (ms) | Space (MB) | Method |\n|-----------|-----------|-------------|-------------|\n| Rust | 0 ms | 2.2 MB | DP |\n| Java | 0 ms | 39.5 MB | DP |\n| C++ | 0 ms | 6.1 MB | DP |\n| Go | 1 ms | 1.9 MB | DP |\n| PHP | 6 ms | 18.8 MB | DP |\n| Python | 26 ms | 16.1 MB | DP |\n| C# | 26 ms | 26.8 MB | DP |\n| Python | 33 ms | 16.4 MB | Recursion |\n| Python | 34 ms | 16.3 MB | Math |\n| JavaScript| 50 ms | 42.2 MB | DP |\n\n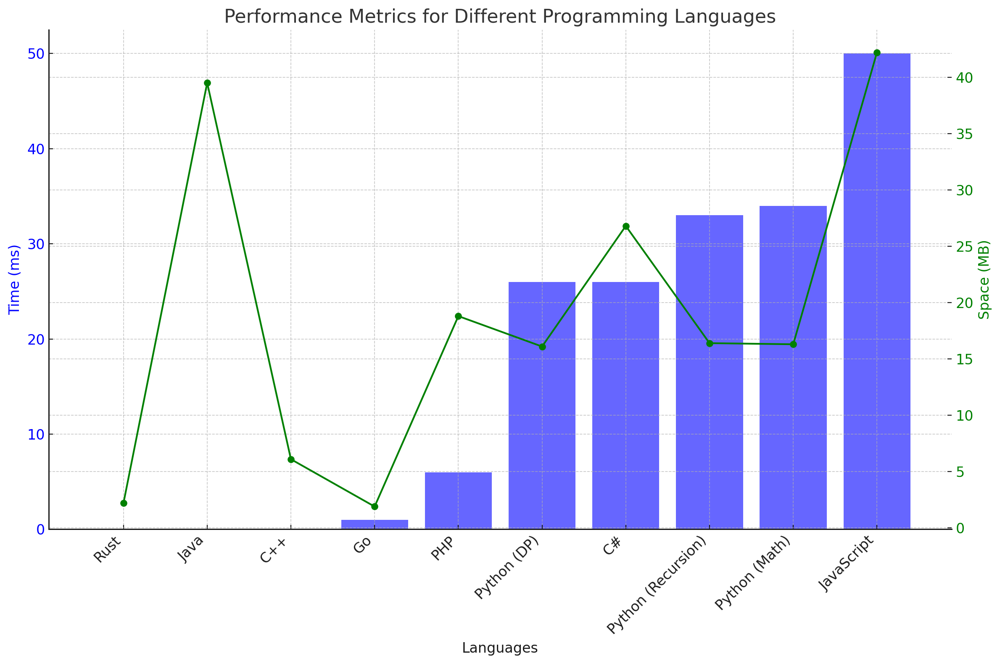\n\n## Live Coding DP & Memo in Go\nhttps://youtu.be/13FJ1NIyE8w?si=1y-HxMjfcD0k99ZQ\n\n## Code Highlights and Best Practices\n\n- All three methods\u2014Dynamic Programming, Recursion with Memoization, and the Mathematical Approach\u2014provide different lenses through which to examine the problem, enhancing your understanding and skills.\n- Dynamic Programming is straightforward, building upon an initial base case.\n- Recursion with Memoization avoids redundant calculations by storing past results.\n- The Mathematical Approach directly computes the answer using combinatorics, reducing the algorithmic complexity.\n\nBy mastering these techniques, you\'ll be well-equipped to tackle similar combinatorial problems that require counting the number of possible sequences or combinations. | 124 | Given `n` orders, each order consist in pickup and delivery services.
Count all valid pickup/delivery possible sequences such that delivery(i) is always after of pickup(i).
Since the answer may be too large, return it modulo 10^9 + 7.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation:** Unique order (P1, D1), Delivery 1 always is after of Pickup 1.
**Example 2:**
**Input:** n = 2
**Output:** 6
**Explanation:** All possible orders:
(P1,P2,D1,D2), (P1,P2,D2,D1), (P1,D1,P2,D2), (P2,P1,D1,D2), (P2,P1,D2,D1) and (P2,D2,P1,D1).
This is an invalid order (P1,D2,P2,D1) because Pickup 2 is after of Delivery 2.
**Example 3:**
**Input:** n = 3
**Output:** 90
**Constraints:**
* `1 <= n <= 500`
Given 2 integers n and start. Your task is return any permutation p of (0,1,2.....,2^n -1) such that : p\[0\] = start, p\[i\] and p\[i+1\] differ by only one bit for all 0 <= i < 2^n - 1. | Use gray code to generate a n-bit sequence. Rotate the sequence such that its first element is start. |
✅ 99.57% DP & Math & Recursion | count-all-valid-pickup-and-delivery-options | 1 | 1 | # Comprehensive Guide to Solving "Count All Valid Pickup and Delivery Options": Dynamic Programming, Recursion, and Math Approaches\n\n## Introduction & Problem Statement\n\nGreetings, aspiring problem solvers! Today we\'ll unravel an intriguing combinatorial problem that revolves around orders, pickups, and deliveries\u2014aptly named **Count All Valid Pickup and Delivery Options**. The problem hands you `n` orders, each consisting of a pickup and delivery service. Your goal is to figure out the number of valid pickup and delivery sequences such that the delivery of each order `i` occurs after its corresponding pickup.\n\n## Key Concepts and Constraints\n\n### What Makes this Problem Unique?\n\n1. **Pairing**: \n Each order contains a pair of services: a pickup (P) and a delivery (D). For order `i`, the pickup is denoted as `P_i` and the delivery as `D_i`.\n \n2. **Order Matters**: \n The sequences are sensitive to the order. `(P1, D1, P2, D2)` is considered different from `(P2, D2, P1, D1)`.\n\n3. **Constraints**: \n - `n` ranges between 1 and 500.\n\n---\n\n# Strategies to Tackle the Problem: A Three-Pronged Approach\n\n## Live Coding 3-in-1 & Explaining\nhttps://youtu.be/wj3vBARk8-U?si=_gFWsftHvd3o_zYN\n\n## Method 1: Dynamic Programming \n\n## What is Dynamic Programming (DP)?\n\nThink of Dynamic Programming as a way to build a solution step-by-step, just like building a LEGO tower. You start with one block and then keep adding more to get the final shape. In a similar way, you start with a simple problem, solve it, and use that solution to solve more complex problems.\n\n## Detailed Steps\n\n### Step 1: Setting a Starting Point (Base Case)\n\n- **Why do we start with `count = 1`?** \n - Imagine you have just one order. This order has one pickup (P1) and one delivery (D1). The only rule is that the delivery (D1) must come after the pickup (P1). This gives you just one way to arrange this order: (P1, D1). So, you start your count at 1.\n\n### Step 2: Building Up the Solution (Iterative Computation)\n\n- **Why do we start the loop from 2?** \n - You\'ve already solved the problem for 1 order. Now you start adding more orders into the mix, one at a time, starting from the second order.\n\n- **What\'s the deal with `2i - 1` and `i`?** \n - Let\'s say you\'re at the `i-th` order. You would have `i` pickups and `i` deliveries, making it `2i` positions in total. \n - Now, when you\'re adding the pickup (Pi) for the `i-th` order, you can put it anywhere except at the end. That\'s `2i - 1` choices for Pi.\n - For Di, you only have `i` choices, because it must come after Pi.\n\n- **How do we update `count`?** \n - Multiply your current count by `(2i - 1) * i` to get the new count. This gives you the total number of sequences for `i` orders.\n\n### Step 3: The Final Answer\n\n- **How do you get the final answer?** \n - After you\'ve gone through all the orders, the value in `count` will be the total number of valid sequences. Return this value.\n\n## Time and Space Complexity\n\n- **Time Complexity**: The solution is speedy; it only takes linear time (`O(n)`).\n \n- **Space Complexity**: We don\'t use much extra space; just one variable (`count`). So the space complexity is `O(1)` or constant.\n\n## Clarification for the Formula `(2i - 1) * i`\n\n- **Why `(2i - 1) * i`?** \n - Think of it this way: for each new order, you have a "slot" for pickup and a "slot" for delivery. The pickup can go in `2i - 1` places, and the delivery in `i` places. You can think of these as dimensions: `2i - 1` for the width and `i` for the height. The total area or number of possibilities is the width multiplied by the height, which is `(2i - 1) * i`.\n\n# Code Dynamic Programming\n``` Python []\nMOD = 10**9 + 7\nclass Solution:\n def countOrders(self, n: int) -> int:\n count = 1 \n for i in range(2, n + 1):\n count = (count * (2 * i - 1) * i) % MOD\n return count\n```\n``` Go []\nconst MOD = 1000000007\n\nfunc countOrders(n int) int {\n count := 1\n for i := 2; i <= n; i++ {\n count = (count * (2 * i - 1) * i) % MOD\n }\n return count\n}\n```\n``` Rust []\nimpl Solution {\n const MOD: i64 = 1_000_000_007;\n \n pub fn count_orders(n: i32) -> i32 {\n let mut count: i64 = 1;\n for i in 2..=n {\n count = (count * ((2 * i - 1) as i64) * (i as i64)) % Self::MOD;\n }\n count as i32\n }\n}\n```\n``` C++ []\nclass Solution {\nconst int MOD = 1e9 + 7;\npublic:\n int countOrders(int n) {\n long long count = 1;\n for (int i = 2; i <= n; ++i) {\n count = (count * (2 * i - 1) * i) % MOD;\n }\n return (int)count;\n }\n};\n```\n``` Java []\npublic class Solution {\n private static final int MOD = 1000000007;\n\n public int countOrders(int n) {\n long count = 1;\n for (int i = 2; i <= n; i++) {\n count = (count * (2 * i - 1) * i) % MOD;\n }\n return (int) count;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} n\n * @return {number}\n */\nconst MOD = 1e9 + 7;\nvar countOrders = function(n) {\n let count = 1;\n for (let i = 2; i <= n; i++) {\n count = (count * (2 * i - 1) * i) % MOD;\n }\n return count;\n}\n```\n``` PHP []\nclass Solution {\n\n const MOD = 1000000007;\n\n /**\n * @param Integer $n\n * @return Integer\n */\n public function countOrders($n) {\n $count = 1;\n for ($i = 2; $i <= $n; $i++) {\n $count = ($count * (2 * $i - 1) * $i) % self::MOD;\n }\n return $count;\n }\n}\n```\n``` C# []\npublic class Solution {\n private const int MOD = 1000000007;\n\n public int CountOrders(int n) {\n long count = 1;\n for (int i = 2; i <= n; i++) {\n count = (count * (2 * i - 1) * i) % MOD;\n }\n return (int)count;\n }\n\n}\n```\n\n---\n\n## Method 2: Recursion with Memoization\n\n## The Sophistication of Memoization\n\nMemoization is an elegant technique that enhances the efficiency of recursive algorithms by storing the results of costly function calls. Imagine having a smart notebook that instantly provides answers to questions you\'ve already solved; that\'s what memoization does for your code.\n\n## A Comprehensive Step-by-Step Guide\n\n### Step 1: Create a Memoization Dictionary\n- **Why Use a Dictionary Called `memo`?** \n - The `memo` dictionary serves as a caching mechanism. It stores the number of valid sequences for a given `n` to avoid recalculating them repeatedly.\n\n### Step 2: Base Case\n- **Why Is the Base Case `n = 1`?** \n - When `n = 1`, there is only a single pair of pickup and delivery. There\'s just one way to sequence this pair\u2014by picking up first and then delivering. Hence, for `n = 1`, there is only one valid sequence.\n\n### Step 3: Recursive Calls Augmented with Memoization\n- **What Happens During the Recursive Calls?** \n - The function calls itself with `n - 1` as the argument.\n - Before diving deeper into recursion, it checks if the result for this `n` is already in `memo`. If so, it returns the stored result.\n - If not, it calculates the number of valid sequences for this `n` using the formula `count = countOrders(n - 1) * (2 * n - 1) * n` and then stores this result in `memo`.\n\n### Step 4: Return the Final Answer\n- **How Do We Get to the Final Answer?** \n - The `memo` dictionary will contain the number of valid sequences for the initial `n`. You simply return this value as the final result.\n\n## Time and Space Complexity Analysis\n\n- **Time Complexity**: `O(n)` \n Each unique value of `n` is calculated only once, and each calculation is done in constant time.\n \n- **Space Complexity**: `O(n)` \n The memoization dictionary stores up to `n` unique entries, making the space complexity linear.\n\n## Code Recursion with Memoization\n``` Python []\nMOD = 10**9 + 7 \nclass Solution:\n memo = {}\n def countOrders(self, n: int) -> int:\n if n == 1:\n return 1\n if n in self.memo:\n return self.memo[n]\n \n count = (self.countOrders(n - 1) * (2 * n - 1) * n) % MOD\n self.memo[n] = count\n return count\n```\n``` Go []\nconst MOD = 1000000007\n\nvar memo = map[int]int{}\n\nfunc countOrders(n int) int {\n\tif n == 1 {\n\t\treturn 1\n\t}\n\tif val, exists := memo[n]; exists {\n\t\treturn val\n\t}\n\n\tcount := (countOrders(n-1) * (2*n - 1) * n) % MOD\n\tmemo[n] = count\n\treturn count\n}\n```\n\n---\n\n## Method 3: The Mathematical Approach \n\n## The Majesty of Mathematics\n\nMathematics is like a teleportation device in the world of algorithms. It can directly take you to the solution, bypassing the need for iterative calculations or recursion.\n\n## A Thorough Step-by-Step Guide\n\n### Step 1: Calculating Factorial and Power\n- **Why Calculate `(2n)!` and `2^n`?** \n - The number of valid sequences can be directly derived using combinatorial mathematics. The formula involves `(2n)!` as well as `2^n`.\n\n### Step 2: Final Calculation and Return\n- **How Is the Final Result Calculated?** \n - The number of valid sequences is given by the formula `(2n)! / 2^n`. This can be calculated using modulo arithmetic to keep the numbers manageable.\n\n## Time and Space Complexity Analysis\n\n- **Time Complexity**: `O(n)` \n Calculating `(2n)!` involves `O(n)` operations.\n \n- **Space Complexity**: `O(1)` \n The space complexity is constant as we only use a few variables to store intermediate and final results.\n\n## Code Mathematical\n``` Python []\nMOD = 10**9 + 7 \nclass Solution:\n def countOrders(self, n: int) -> int:\n two_n_fact = factorial(2 * n) % MOD\n two_pow_n = pow(2, n, MOD)\n return (two_n_fact * pow(two_pow_n, -1, MOD)) % MOD\n```\n``` Go []\nconst MOD = 1000000007\n\nfunc factorial(n int) int {\n\tresult := 1\n\tfor i := 1; i <= n; i++ {\n\t\tresult = (result * i) % MOD\n\t}\n\treturn result\n}\n\nfunc pow(base, exp, mod int) int {\n\tresult := 1\n\tfor exp > 0 {\n\t\tif exp%2 == 1 {\n\t\t\tresult = (result * base) % mod\n\t\t}\n\t\tbase = (base * base) % mod\n\t\texp /= 2\n\t}\n\treturn result\n}\n\nfunc countOrders(n int) int {\n\ttwoNFact := factorial(2 * n) % MOD\n\ttwoPowN := pow(2, n, MOD)\n\treturn (twoNFact * pow(twoPowN, MOD-2, MOD)) % MOD\n}\n```\n\n## Performance\n\n| Language | Time (ms) | Space (MB) | Method |\n|-----------|-----------|-------------|-------------|\n| Rust | 0 ms | 2.2 MB | DP |\n| Java | 0 ms | 39.5 MB | DP |\n| C++ | 0 ms | 6.1 MB | DP |\n| Go | 1 ms | 1.9 MB | DP |\n| PHP | 6 ms | 18.8 MB | DP |\n| Python | 26 ms | 16.1 MB | DP |\n| C# | 26 ms | 26.8 MB | DP |\n| Python | 33 ms | 16.4 MB | Recursion |\n| Python | 34 ms | 16.3 MB | Math |\n| JavaScript| 50 ms | 42.2 MB | DP |\n\n\n\n## Live Coding DP & Memo in Go\nhttps://youtu.be/13FJ1NIyE8w?si=1y-HxMjfcD0k99ZQ\n\n## Code Highlights and Best Practices\n\n- All three methods\u2014Dynamic Programming, Recursion with Memoization, and the Mathematical Approach\u2014provide different lenses through which to examine the problem, enhancing your understanding and skills.\n- Dynamic Programming is straightforward, building upon an initial base case.\n- Recursion with Memoization avoids redundant calculations by storing past results.\n- The Mathematical Approach directly computes the answer using combinatorics, reducing the algorithmic complexity.\n\nBy mastering these techniques, you\'ll be well-equipped to tackle similar combinatorial problems that require counting the number of possible sequences or combinations. | 124 | Given a binary string `s` and an integer `k`, return `true` _if every binary code of length_ `k` _is a substring of_ `s`. Otherwise, return `false`.
**Example 1:**
**Input:** s = "00110110 ", k = 2
**Output:** true
**Explanation:** The binary codes of length 2 are "00 ", "01 ", "10 " and "11 ". They can be all found as substrings at indices 0, 1, 3 and 2 respectively.
**Example 2:**
**Input:** s = "0110 ", k = 1
**Output:** true
**Explanation:** The binary codes of length 1 are "0 " and "1 ", it is clear that both exist as a substring.
**Example 3:**
**Input:** s = "0110 ", k = 2
**Output:** false
**Explanation:** The binary code "00 " is of length 2 and does not exist in the array.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= k <= 20` | Use the permutation and combination theory to add one (P, D) pair each time until n pairs. |
Python shortest 1-liner. Functional programming. | count-all-valid-pickup-and-delivery-options | 0 | 1 | # Approach\n$$ways(n) = \\left(\\sum_{x=1}^{2(n-1)+1} x\\right) \\cdot ways(n-1) = 2n! \\div 2^n$$\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```python\nclass Solution:\n def countOrders(self, n: int) -> int:\n return (factorial(2 * n) // pow(2, n)) % 1_000_000_007\n\n\n``` | 2 | Given `n` orders, each order consist in pickup and delivery services.
Count all valid pickup/delivery possible sequences such that delivery(i) is always after of pickup(i).
Since the answer may be too large, return it modulo 10^9 + 7.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation:** Unique order (P1, D1), Delivery 1 always is after of Pickup 1.
**Example 2:**
**Input:** n = 2
**Output:** 6
**Explanation:** All possible orders:
(P1,P2,D1,D2), (P1,P2,D2,D1), (P1,D1,P2,D2), (P2,P1,D1,D2), (P2,P1,D2,D1) and (P2,D2,P1,D1).
This is an invalid order (P1,D2,P2,D1) because Pickup 2 is after of Delivery 2.
**Example 3:**
**Input:** n = 3
**Output:** 90
**Constraints:**
* `1 <= n <= 500`
Given 2 integers n and start. Your task is return any permutation p of (0,1,2.....,2^n -1) such that : p\[0\] = start, p\[i\] and p\[i+1\] differ by only one bit for all 0 <= i < 2^n - 1. | Use gray code to generate a n-bit sequence. Rotate the sequence such that its first element is start. |
Python shortest 1-liner. Functional programming. | count-all-valid-pickup-and-delivery-options | 0 | 1 | # Approach\n$$ways(n) = \\left(\\sum_{x=1}^{2(n-1)+1} x\\right) \\cdot ways(n-1) = 2n! \\div 2^n$$\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```python\nclass Solution:\n def countOrders(self, n: int) -> int:\n return (factorial(2 * n) // pow(2, n)) % 1_000_000_007\n\n\n``` | 2 | Given a binary string `s` and an integer `k`, return `true` _if every binary code of length_ `k` _is a substring of_ `s`. Otherwise, return `false`.
**Example 1:**
**Input:** s = "00110110 ", k = 2
**Output:** true
**Explanation:** The binary codes of length 2 are "00 ", "01 ", "10 " and "11 ". They can be all found as substrings at indices 0, 1, 3 and 2 respectively.
**Example 2:**
**Input:** s = "0110 ", k = 1
**Output:** true
**Explanation:** The binary codes of length 1 are "0 " and "1 ", it is clear that both exist as a substring.
**Example 3:**
**Input:** s = "0110 ", k = 2
**Output:** false
**Explanation:** The binary code "00 " is of length 2 and does not exist in the array.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= k <= 20` | Use the permutation and combination theory to add one (P, D) pair each time until n pairs. |
Python3 Solution | count-all-valid-pickup-and-delivery-options | 0 | 1 | \n```\nclass Solution:\n def countOrders(self, n: int) -> int:\n mod=10**9+7\n ans=math.factorial(n*2)>>n\n return ans%mod\n``` | 2 | Given `n` orders, each order consist in pickup and delivery services.
Count all valid pickup/delivery possible sequences such that delivery(i) is always after of pickup(i).
Since the answer may be too large, return it modulo 10^9 + 7.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation:** Unique order (P1, D1), Delivery 1 always is after of Pickup 1.
**Example 2:**
**Input:** n = 2
**Output:** 6
**Explanation:** All possible orders:
(P1,P2,D1,D2), (P1,P2,D2,D1), (P1,D1,P2,D2), (P2,P1,D1,D2), (P2,P1,D2,D1) and (P2,D2,P1,D1).
This is an invalid order (P1,D2,P2,D1) because Pickup 2 is after of Delivery 2.
**Example 3:**
**Input:** n = 3
**Output:** 90
**Constraints:**
* `1 <= n <= 500`
Given 2 integers n and start. Your task is return any permutation p of (0,1,2.....,2^n -1) such that : p\[0\] = start, p\[i\] and p\[i+1\] differ by only one bit for all 0 <= i < 2^n - 1. | Use gray code to generate a n-bit sequence. Rotate the sequence such that its first element is start. |
Python3 Solution | count-all-valid-pickup-and-delivery-options | 0 | 1 | \n```\nclass Solution:\n def countOrders(self, n: int) -> int:\n mod=10**9+7\n ans=math.factorial(n*2)>>n\n return ans%mod\n``` | 2 | Given a binary string `s` and an integer `k`, return `true` _if every binary code of length_ `k` _is a substring of_ `s`. Otherwise, return `false`.
**Example 1:**
**Input:** s = "00110110 ", k = 2
**Output:** true
**Explanation:** The binary codes of length 2 are "00 ", "01 ", "10 " and "11 ". They can be all found as substrings at indices 0, 1, 3 and 2 respectively.
**Example 2:**
**Input:** s = "0110 ", k = 1
**Output:** true
**Explanation:** The binary codes of length 1 are "0 " and "1 ", it is clear that both exist as a substring.
**Example 3:**
**Input:** s = "0110 ", k = 2
**Output:** false
**Explanation:** The binary code "00 " is of length 2 and does not exist in the array.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= k <= 20` | Use the permutation and combination theory to add one (P, D) pair each time until n pairs. |
【Video】Easy way to think about this question! - Python, JavaScript, Java and C++ | count-all-valid-pickup-and-delivery-options | 1 | 1 | # Intuition\nBreak down the question into a small case, so that you can understand it easily.\n\n---\n\n# Solution Video\n\n### \u2B50\uFE0F Please subscribe to my channel from here. I have 258 videos as of September 10th, 2023.\n\nIn the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\nhttps://youtu.be/YcTGeVXwWhs\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2274\nThank you for your support!\n\n---\n\n# Approach\nLet\'s think about n = 2\n\nif n is 1, we have one combination like this.\n```\nP1 D1\n```\n\nwhen n = 2, let\'s insert P2 and D2 into P1 D1.\n\n```\nP2 D2 P1 D1\nP2 P1 D2 D1\nP2 P1 D1 D2\n```\n\nThe same situation happens to P1 D1 inserted into P2 D2\n\n```\nP1 D1 P2 D2\nP1 P2 D1 D2\nP1 P2 D2 D1\n```\n\nMain point of logic is here.\n```\ntotal_ways = (total_ways * (2 * order_number - 1) * order_number) % MOD\n```\nRegarding `(2 * order_number - 1)`, this indicates this part.\n\n```\nP2 D2 P1 D1\nP2 P1 D2 D1\nP2 P1 D1 D2\n```\n\nWe have 2 choice(pickup and delivery) for one order. That\'s why we have `2 * order_number` combination which is 4, but we can put D2 in 3 places(_) like this.\n\n```\nP2 _ P1 D1\nP2 P1 _ D1\nP2 P1 D1 _\n```\n\nBecause P2 is in the first place and D2 must be after P2, so number of combiantions should be 3. We need to subtract -1 from 4 which is 3.\n\nSince the same situation happens to P1 D1 inserted into P2 D2, we need to multiply `order_number` with `(2 * order_number - 1)`. In the end we get this formula.\n\n```\n(2 * order_number - 1) * order_number)\n```\n\nAlso this is combination number, so we need to `multiply total_ways so far with (2 * order_number - 1) * order_number`. The final formula of the main point should be\n\n```\ntotal_ways = (total_ways * (2 * order_number - 1) * order_number) % MOD\n```\n\n# Complexity\n- Time complexity: O(n)\nThe code uses a for loop that iterates from 2 to n. In each iteration, it performs a constant number of arithmetic operations. Therefore, the time complexity of this code is O(n).\n\n- Space complexity: O(1)\nThe code uses a constant amount of extra space for variables like MOD, total_ways, and the loop control variable order_number. It does not use any data structures that would grow with the input size n. Thus, the space complexity of this code is O(1), which means it has constant space complexity.\n\n```python []\nclass Solution:\n def countOrders(self, n: int) -> int:\n MOD = 10**9 + 7\n total_ways = 1 \n for order_number in range(2, n + 1):\n total_ways = (total_ways * (2 * order_number - 1) * order_number) % MOD\n return total_ways\n```\n```javascript []\n/**\n * @param {number} n\n * @return {number}\n */\nvar countOrders = function(n) {\n const MOD = 1000000007;\n let totalWays = 1;\n for (let orderNumber = 2; orderNumber <= n; orderNumber++) {\n totalWays = (totalWays * (2 * orderNumber - 1) * orderNumber) % MOD;\n }\n return totalWays; \n};\n```\n```java []\nclass Solution {\n public int countOrders(int n) {\n final int MOD = 1000000007;\n int totalWays = 1;\n for (int orderNumber = 2; orderNumber <= n; orderNumber++) {\n totalWays = (int)((totalWays * (2L * orderNumber - 1) * orderNumber) % MOD);\n }\n return totalWays; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int countOrders(int n) {\n const int MOD = 1000000007;\n long long totalWays = 1;\n for (int orderNumber = 2; orderNumber <= n; orderNumber++) {\n totalWays = (totalWays * (2LL * orderNumber - 1) * orderNumber) % MOD;\n }\n return static_cast<int>(totalWays); \n }\n};\n```\n\n\n---\n\n\nI started creating basic programming course with Python. This is the second video I created yesterday. Please check if you like.\n\nhttps://youtu.be/_083XcC9lVc\n | 30 | Given `n` orders, each order consist in pickup and delivery services.
Count all valid pickup/delivery possible sequences such that delivery(i) is always after of pickup(i).
Since the answer may be too large, return it modulo 10^9 + 7.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation:** Unique order (P1, D1), Delivery 1 always is after of Pickup 1.
**Example 2:**
**Input:** n = 2
**Output:** 6
**Explanation:** All possible orders:
(P1,P2,D1,D2), (P1,P2,D2,D1), (P1,D1,P2,D2), (P2,P1,D1,D2), (P2,P1,D2,D1) and (P2,D2,P1,D1).
This is an invalid order (P1,D2,P2,D1) because Pickup 2 is after of Delivery 2.
**Example 3:**
**Input:** n = 3
**Output:** 90
**Constraints:**
* `1 <= n <= 500`
Given 2 integers n and start. Your task is return any permutation p of (0,1,2.....,2^n -1) such that : p\[0\] = start, p\[i\] and p\[i+1\] differ by only one bit for all 0 <= i < 2^n - 1. | Use gray code to generate a n-bit sequence. Rotate the sequence such that its first element is start. |
【Video】Easy way to think about this question! - Python, JavaScript, Java and C++ | count-all-valid-pickup-and-delivery-options | 1 | 1 | # Intuition\nBreak down the question into a small case, so that you can understand it easily.\n\n---\n\n# Solution Video\n\n### \u2B50\uFE0F Please subscribe to my channel from here. I have 258 videos as of September 10th, 2023.\n\nIn the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\nhttps://youtu.be/YcTGeVXwWhs\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2274\nThank you for your support!\n\n---\n\n# Approach\nLet\'s think about n = 2\n\nif n is 1, we have one combination like this.\n```\nP1 D1\n```\n\nwhen n = 2, let\'s insert P2 and D2 into P1 D1.\n\n```\nP2 D2 P1 D1\nP2 P1 D2 D1\nP2 P1 D1 D2\n```\n\nThe same situation happens to P1 D1 inserted into P2 D2\n\n```\nP1 D1 P2 D2\nP1 P2 D1 D2\nP1 P2 D2 D1\n```\n\nMain point of logic is here.\n```\ntotal_ways = (total_ways * (2 * order_number - 1) * order_number) % MOD\n```\nRegarding `(2 * order_number - 1)`, this indicates this part.\n\n```\nP2 D2 P1 D1\nP2 P1 D2 D1\nP2 P1 D1 D2\n```\n\nWe have 2 choice(pickup and delivery) for one order. That\'s why we have `2 * order_number` combination which is 4, but we can put D2 in 3 places(_) like this.\n\n```\nP2 _ P1 D1\nP2 P1 _ D1\nP2 P1 D1 _\n```\n\nBecause P2 is in the first place and D2 must be after P2, so number of combiantions should be 3. We need to subtract -1 from 4 which is 3.\n\nSince the same situation happens to P1 D1 inserted into P2 D2, we need to multiply `order_number` with `(2 * order_number - 1)`. In the end we get this formula.\n\n```\n(2 * order_number - 1) * order_number)\n```\n\nAlso this is combination number, so we need to `multiply total_ways so far with (2 * order_number - 1) * order_number`. The final formula of the main point should be\n\n```\ntotal_ways = (total_ways * (2 * order_number - 1) * order_number) % MOD\n```\n\n# Complexity\n- Time complexity: O(n)\nThe code uses a for loop that iterates from 2 to n. In each iteration, it performs a constant number of arithmetic operations. Therefore, the time complexity of this code is O(n).\n\n- Space complexity: O(1)\nThe code uses a constant amount of extra space for variables like MOD, total_ways, and the loop control variable order_number. It does not use any data structures that would grow with the input size n. Thus, the space complexity of this code is O(1), which means it has constant space complexity.\n\n```python []\nclass Solution:\n def countOrders(self, n: int) -> int:\n MOD = 10**9 + 7\n total_ways = 1 \n for order_number in range(2, n + 1):\n total_ways = (total_ways * (2 * order_number - 1) * order_number) % MOD\n return total_ways\n```\n```javascript []\n/**\n * @param {number} n\n * @return {number}\n */\nvar countOrders = function(n) {\n const MOD = 1000000007;\n let totalWays = 1;\n for (let orderNumber = 2; orderNumber <= n; orderNumber++) {\n totalWays = (totalWays * (2 * orderNumber - 1) * orderNumber) % MOD;\n }\n return totalWays; \n};\n```\n```java []\nclass Solution {\n public int countOrders(int n) {\n final int MOD = 1000000007;\n int totalWays = 1;\n for (int orderNumber = 2; orderNumber <= n; orderNumber++) {\n totalWays = (int)((totalWays * (2L * orderNumber - 1) * orderNumber) % MOD);\n }\n return totalWays; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int countOrders(int n) {\n const int MOD = 1000000007;\n long long totalWays = 1;\n for (int orderNumber = 2; orderNumber <= n; orderNumber++) {\n totalWays = (totalWays * (2LL * orderNumber - 1) * orderNumber) % MOD;\n }\n return static_cast<int>(totalWays); \n }\n};\n```\n\n\n---\n\n\nI started creating basic programming course with Python. This is the second video I created yesterday. Please check if you like.\n\nhttps://youtu.be/_083XcC9lVc\n | 30 | Given a binary string `s` and an integer `k`, return `true` _if every binary code of length_ `k` _is a substring of_ `s`. Otherwise, return `false`.
**Example 1:**
**Input:** s = "00110110 ", k = 2
**Output:** true
**Explanation:** The binary codes of length 2 are "00 ", "01 ", "10 " and "11 ". They can be all found as substrings at indices 0, 1, 3 and 2 respectively.
**Example 2:**
**Input:** s = "0110 ", k = 1
**Output:** true
**Explanation:** The binary codes of length 1 are "0 " and "1 ", it is clear that both exist as a substring.
**Example 3:**
**Input:** s = "0110 ", k = 2
**Output:** false
**Explanation:** The binary code "00 " is of length 2 and does not exist in the array.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= k <= 20` | Use the permutation and combination theory to add one (P, D) pair each time until n pairs. |
🚀 Beats 100% || C++ || Java || Python || DP Recursive & Iterative || Commented Code🚀 | count-all-valid-pickup-and-delivery-options | 1 | 1 | # Problem Description\n\nYou are given `n` orders, each comprising both **pickup** and **delivery** services. The task is to **count** all the valid sequences of these orders, ensuring that the delivery for each order always occurs after its corresponding pickup. To manage large results, return the count modulo `10^9 + 7`.\n\n- **Constraints:**\n - 1 <= n <= 500\n - Return result modulo `10^9 + 7`.\n - Pickup must occur **before** its corresponding delivery.\n\n---\n\n# Dynamic Programming\n\n\n\n**Dynamic Programming** is a powerful technique that involves **caching** pre-computed results, thereby **eliminating** the need for redundant computations and significantly **optimizing** time complexity.\nThere are **two primary approaches** to Dynamic Programming:\n\n## Recursive Approach (Top-Down)\nWe can think of Recursive Approach as **breaking** hard bricks into **small** rocks. but, how this apply to our problem ?\nWe can **break** our **complex problem** into **easier** ones. so we can calculate the result for the `n` pairs by calculate the answer for `n - 1` pairs which is easier and use its result as part of our solution.\n\n## Iterative Approach (Bottom-Up)\nWe can think of Iterative Approach as **building** high building from small bricks. but, how this also apply to our problem ?\nWe can **solve** our **complex problem** by solving **easier** ones first and build until we reach our complex problem. so we can calculate first the result for one pair then 2, 3, 4..... and build our table of solutions until we reach `n` pairs.\n\n---\n# Intuition\nFor now let\'s **assume** that we don\'t need the delivery to occur after its corresponding pickup.\nLet\'s start by **general** solution that we have `(n-1)` pairs and we want to find the number of combinations to **insert** the `n-th` pair\nif we looked at our image (where we assume n = 4 ) we can find that we have `(n-1) * 2` item and we can insert our two new items anywhere between them.\n\n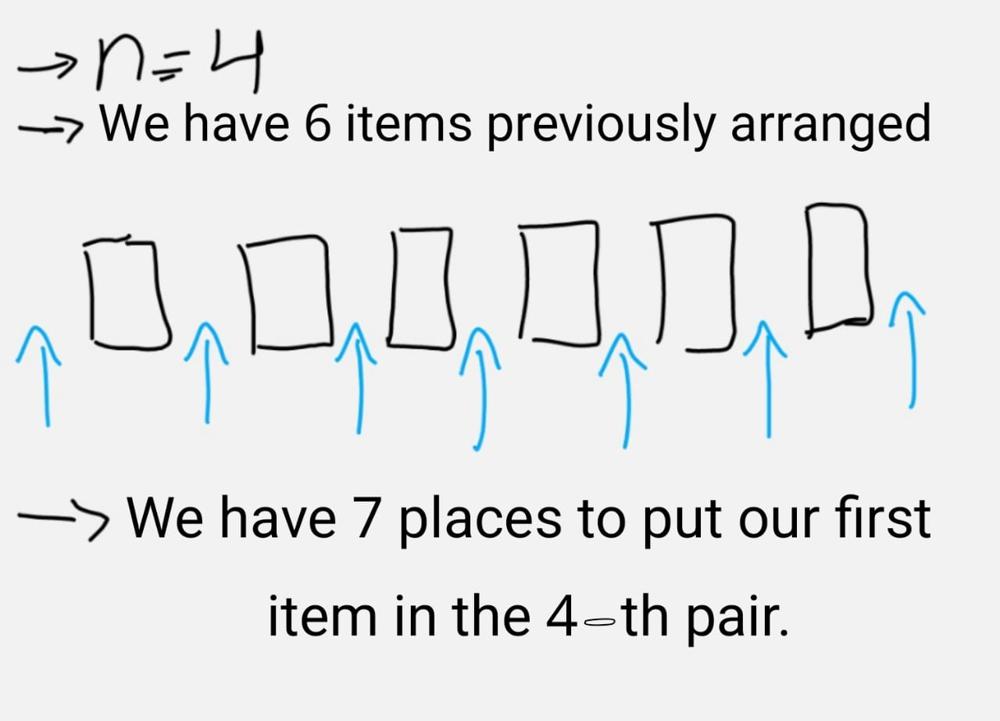\n\nFor our **first item** in `n-th` pair, we have `(n * 2 - 1)` new places to replace our new item.\nFor our **second item** in `n-th` pair, we have `(n * 2)` places to replace it. **Remember** that we already replaced the first item in the pair in it. \nSo from this places, we can conclude that we have `(n * 2 - 1) * n * 2` places to replace our two new items. \n\nLet\'s now **forget our assumption** that we talked about before, since we only need the pickup to occur **before** its corresponding delivery. Since the order matters here such that the **pickup** must occur **before** its **delivery** so half of our combinations are unacceptable -the combinations that the pickup will occur after its delivery- and the other half is our desired solution -the combinations that the pickup will occur before its delivery-.\n\nAccording to that, we will **divide our formula by two** and we will have `(n * 2 - 1) * n` number of ways to insert our `n-th` pair and we will calculate our **final solution** by **multiplying** the number of combinations to insert every `n-th` pair into the `n-1 th` pair starting from `1` going up to `n`. \n\n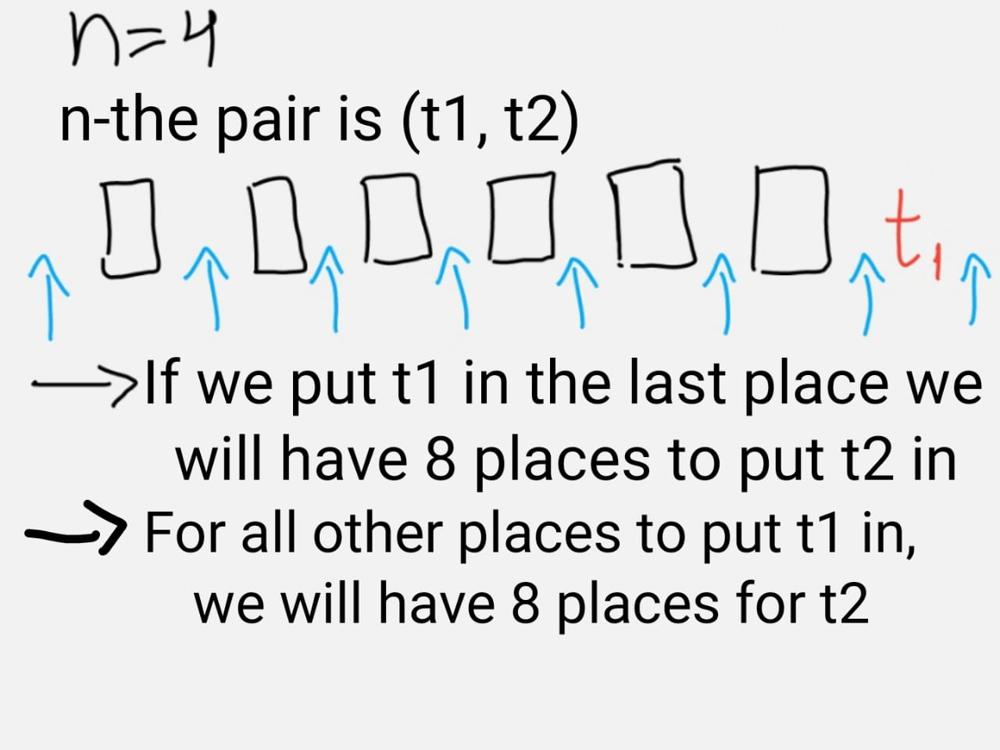\n\n\n---\n\n\n# Proposed Solutions\n## 1. Recursive Approach (Top-Down)\n### Approach\n- Create a memoization vector to store computed values.\n- Recursive Function **calculateOrdersCount:**\n - Calculate the number of valid orders for remainingPairs using recursion and memoization.\n - **Base case**: If remainingPairs is 0, return 1.\n - Otherwise, calculate it using the formula `(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % MOD` and memoize the result.\n \n- Main Function **countOrders**:\n - **Initialize** memoization with -1 values.\n - Call **calculateOrdersCount** with numPairs to find the count of valid orders.\n - **Return** Result.\n\n### Complexity\n- **Time complexity:** $$O(N)$$\nWe are calculating the number of combinations for all pairs from n until we reach 1, so time complexity is `O(N)`.\n\n- **Space complexity:** $$O(N)$$\nWe are storing the array we are using for dynamic programming with size `n` and we are making recursive call with depth maximum `n` which is `2*N` space, so space complexity is `O(N)`.\n\n## 2. Iterative Approach (Bottom-Up)\n### Approach\n- Create a memoization array dp of size `numberOfPairs + 1`.\n- **Base Case:** Set dp[0] to 1, representing the one way to arrange 0 pairs.\n- Calculate Valid Orders **Iteratively**\n - Loop from 1 to numberOfPairs inclusive.\n - For each value of currentPairs, calculate dp[currentPairs] using the formula: `dp[currentPairs] = dp[currentPairs - 1] * (2 * currentPairs - 1) * currentPairs % MOD`.\n- **Return** Result.\n\n### Complexity\n- **Time complexity:** $$O(N)$$\nWe are calculating the number of combinations for all pairs from 1 until we reach n, so time complexity is `O(N)`\n\n- **Space complexity:** $$O(N)$$\nWe are storing the array we are using for dynamic programming with size `n`, so space complexity is `O(N)`.\n\n---\n\n\n# Code\n## 1. Recursive Approach (Top-Down)\n```C++ []\nclass Solution {\npublic:\n const int MOD = 1e9 + 7; // Modulus for calculations\n vector<long long> memoization; // Memoization array to store computed values\n\n long long calculateOrdersCount(long long remainingPairs) {\n // Base case: No remaining pairs, return 1\n if (remainingPairs == 0)\n return 1;\n\n // Check if the value is already computed and return it\n if (memoization[remainingPairs] != -1)\n return memoization[remainingPairs];\n\n // Calculate the number of valid orders for the remaining pairs\n long long currentResult = calculateOrdersCount(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % MOD;\n\n // Store the result in the memoization array and return it\n return memoization[remainingPairs] = currentResult;\n }\n\n int countOrders(int numPairs) {\n // Initialize the memoization array with -1 values\n memoization.resize(numPairs + 1, -1);\n\n // Calculate and return the count of valid orders\n return calculateOrdersCount(numPairs);\n }\n};\n```\n```Java []\nclass Solution {\n\n private int MOD = (int)1e9 + 7; // Modulus for calculations\n private static final int MAX_PAIRS = 510; // Maximum possible pairs value\n private long[] memoization = new long[MAX_PAIRS]; // Memoization array to store computed values\n\n private long calculateOrdersCount(long remainingPairs) {\n // Base case: No remaining pairs, return 1\n if (remainingPairs == 0)\n return 1;\n\n // Check if the value is already computed and return it\n if (memoization[(int)remainingPairs] != -1)\n return memoization[(int)remainingPairs];\n\n // Calculate the number of valid orders for the remaining pairs\n long currentResult = calculateOrdersCount(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % MOD;\n\n // Store the result in the memoization array and return it\n return memoization[(int)remainingPairs] = currentResult;\n }\n\n public int countOrders(int numPairs) {\n // Initialize the memoization array with -1 values\n for(int i = 0 ; i < numPairs + 5 ; i ++){\n memoization[i] = -1 ;\n }\n\n // Calculate and return the count of valid orders\n return (int)calculateOrdersCount(numPairs);\n }\n}\n```\n```Python []\nclass Solution:\n def __init__(self):\n self.MOD = int(1e9 + 7) # Modulus for calculations\n self.memoization = [] # Memoization array to store computed values\n\n def calculateOrdersCount(self, remainingPairs):\n # Base case: No remaining pairs, return 1\n if remainingPairs == 0:\n return 1\n\n # Check if the value is already computed and return it\n if self.memoization[remainingPairs] != -1:\n return self.memoization[remainingPairs]\n\n # Calculate the number of valid orders for the remaining pairs\n currentResult = self.calculateOrdersCount(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % self.MOD\n\n # Store the result in the memoization array and return it\n self.memoization[remainingPairs] = currentResult\n return currentResult\n\n def countOrders(self, numPairs):\n # Initialize the memoization array with -1 values\n self.memoization = [-1] * (numPairs + 1)\n\n # Calculate and return the count of valid orders\n return self.calculateOrdersCount(numPairs)\n```\n\n## 2. Iterative Approach (Bottom-Up) \n```C++ []\nclass Solution {\npublic:\n const int MOD = 1e9 + 7; // Modulus for calculations\n vector<long long> dp; // Array for memoization\n\n int countOrders(int numberOfPairs) {\n dp.resize(numberOfPairs + 1); // Initialize memoization array\n\n // Base case: there is one way to arrange 0 pairs\n dp[0] = 1;\n\n // Iterate over all values of pairs from 1 to n\n for (int currentPairs = 1; currentPairs <= numberOfPairs; currentPairs++) {\n // Calculate the number of valid orders for the current number of pairs\n dp[currentPairs] = dp[currentPairs - 1] * (2 * currentPairs - 1) * currentPairs % MOD;\n }\n\n return dp[numberOfPairs]; // Return the result for n pairs\n }\n};\n```\n```Java []\nclass Solution {\n\n private int MOD = (int)1e9 + 7; // Modulus for calculations\n\n public int countOrders(int numPairs) {\n // Memoization array to store computed values\n long[] dp = new long[numPairs + 1];\n\n // Base case: there is one way to arrange 0 pairs\n dp[0] = 1;\n\n // Iterate over all values of pairs from 1 to n\n for (int currentPairs = 1; currentPairs <= numPairs; currentPairs++) {\n // Calculate the number of valid orders for the current number of pairs\n dp[currentPairs] = dp[currentPairs - 1] * (2 * currentPairs - 1) * currentPairs % MOD;\n }\n\n return (int)dp[numPairs]; // Return the result for n pairs\n }\n}\n```\n```Python []\nclass Solution:\n def countOrders(self, numPairs: int) -> int:\n MOD = int(1e9 + 7) # Modulus for calculations\n MAX_PAIRS = numPairs + 1 # Maximum possible pairs value\n\n # Initialize the memoization array with -1 values\n dp = [0] * MAX_PAIRS\n\n # Base case: there is one way to arrange 0 pairs\n dp[0] = 1\n\n # Iterate over all values of pairs from 1 to n\n for currentPairs in range(1, numPairs + 1) :\n # Calculate the number of valid orders for the current number of pairs\n dp[currentPairs] = dp[currentPairs - 1] * (2 * currentPairs - 1) * currentPairs % MOD;\n\n # Return the result for n pairs\n return dp[numPairs]; \n```\n\n\n---\n\n\n# No need of DP array?\nYes, in the proposed approaches -Recursive and Iterative-, we can only **use one variable** instead of using dp array to store all of the cases.\n\nIs using one variable instead of an array is **considered as DP** ?\n**Yes**, we can say that using one variable in considered as DP since it has the **core of DP** which is caching the results that we will use it later instead of re-calculate it again even if it was one variable.\n\nUsing one variable will only affect the **space complexity**:\n- In the **Recursive approach** instead of `2*N` it will only be `N` which is the depth of the recursive call stack so `O(N)`\n- In the **Iterative approach** it will be `O(1)` since we only storing one variable without recursive calls.\n\n\n## Code\n## 1. Recursive Approach (Top-Down)\n```C++ []\nclass Solution {\n public:\n int MOD = (int)1e9 + 7; // Modulus for calculations\n\n long long calculateOrdersCount(long long remainingPairs) {\n // Base case: No remaining pairs, return 1\n if (remainingPairs == 0)\n return 1;\n\n // Calculate the number of valid orders for the remaining pairs\n long long currentResult = calculateOrdersCount(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % MOD;\n\n return currentResult;\n }\n\n int countOrders(int numPairs) {\n // Calculate and return the count of valid orders\n return calculateOrdersCount(numPairs);\n }\n};\n```\n```Java []\nclass Solution {\n\n private int MOD = (int)1e9 + 7; // Modulus for calculations\n\n private long calculateOrdersCount(long remainingPairs) {\n // Base case: No remaining pairs, return 1\n if (remainingPairs == 0)\n return 1;\n\n // Calculate the number of valid orders for the remaining pairs\n long currentResult = calculateOrdersCount(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % MOD;\n\n return currentResult;\n }\n\n public int countOrders(int numPairs) {\n // Calculate and return the count of valid orders\n return (int)calculateOrdersCount(numPairs);\n }\n}\n```\n```Python []\nclass Solution:\n def __init__(self):\n self.MOD = int(1e9 + 7) # Modulus for calculations\n\n def calculateOrdersCount(self, remainingPairs):\n # Base case: No remaining pairs, return 1\n if remainingPairs == 0:\n return 1\n\n # Calculate the number of valid orders for the remaining pairs\n currentResult = self.calculateOrdersCount(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % self.MOD\n\n return currentResult\n\n def countOrders(self, numPairs):\n # Calculate and return the count of valid orders\n return self.calculateOrdersCount(numPairs)\n```\n\n## 2. Iterative Approach (Bottom-Up) \n```C++ []\nclass Solution {\npublic:\n const int MOD = 1e9 + 7; // Modulus for calculations\n\n int countOrders(int numberOfPairs) {\n long long count = 1 ;\n\n // Iterate over all values of pairs from 1 to n\n for (int currentPairs = 1; currentPairs <= numberOfPairs; currentPairs++) {\n // Calculate the number of valid orders for the current number of pairs\n count = count * (2 * currentPairs - 1) * currentPairs % MOD;\n }\n\n return count; // Return the result for n pairs\n }\n};\n```\n```Java []\nclass Solution {\n private int MOD = (int)1e9 + 7; // Modulus for calculations\n\n public int countOrders(int numberOfPairs) {\n long count = 1 ;\n\n // Iterate over all values of pairs from 1 to n\n for (int currentPairs = 1; currentPairs <= numberOfPairs; currentPairs++) {\n // Calculate the number of valid orders for the current number of pairs\n count = count * (2 * currentPairs - 1) * currentPairs % MOD;\n }\n\n return (int)count; // Return the result for n pairs\n }\n};\n```\n```Python []\nclass Solution:\n def countOrders(self, numPairs: int) -> int:\n MOD = int(1e9 + 7) # Modulus for calculations\n\n count = 1\n\n # Iterate over all values of pairs from 1 to n\n for currentPairs in range(1, numPairs + 1) :\n # Calculate the number of valid orders for the current number of pairs\n count = count * (2 * currentPairs - 1) * currentPairs % MOD;\n\n # Return the result for n pairs\n return count; \n```\n\n\n\n\n\n\n | 62 | Given `n` orders, each order consist in pickup and delivery services.
Count all valid pickup/delivery possible sequences such that delivery(i) is always after of pickup(i).
Since the answer may be too large, return it modulo 10^9 + 7.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation:** Unique order (P1, D1), Delivery 1 always is after of Pickup 1.
**Example 2:**
**Input:** n = 2
**Output:** 6
**Explanation:** All possible orders:
(P1,P2,D1,D2), (P1,P2,D2,D1), (P1,D1,P2,D2), (P2,P1,D1,D2), (P2,P1,D2,D1) and (P2,D2,P1,D1).
This is an invalid order (P1,D2,P2,D1) because Pickup 2 is after of Delivery 2.
**Example 3:**
**Input:** n = 3
**Output:** 90
**Constraints:**
* `1 <= n <= 500`
Given 2 integers n and start. Your task is return any permutation p of (0,1,2.....,2^n -1) such that : p\[0\] = start, p\[i\] and p\[i+1\] differ by only one bit for all 0 <= i < 2^n - 1. | Use gray code to generate a n-bit sequence. Rotate the sequence such that its first element is start. |
🚀 Beats 100% || C++ || Java || Python || DP Recursive & Iterative || Commented Code🚀 | count-all-valid-pickup-and-delivery-options | 1 | 1 | # Problem Description\n\nYou are given `n` orders, each comprising both **pickup** and **delivery** services. The task is to **count** all the valid sequences of these orders, ensuring that the delivery for each order always occurs after its corresponding pickup. To manage large results, return the count modulo `10^9 + 7`.\n\n- **Constraints:**\n - 1 <= n <= 500\n - Return result modulo `10^9 + 7`.\n - Pickup must occur **before** its corresponding delivery.\n\n---\n\n# Dynamic Programming\n\n\n\n**Dynamic Programming** is a powerful technique that involves **caching** pre-computed results, thereby **eliminating** the need for redundant computations and significantly **optimizing** time complexity.\nThere are **two primary approaches** to Dynamic Programming:\n\n## Recursive Approach (Top-Down)\nWe can think of Recursive Approach as **breaking** hard bricks into **small** rocks. but, how this apply to our problem ?\nWe can **break** our **complex problem** into **easier** ones. so we can calculate the result for the `n` pairs by calculate the answer for `n - 1` pairs which is easier and use its result as part of our solution.\n\n## Iterative Approach (Bottom-Up)\nWe can think of Iterative Approach as **building** high building from small bricks. but, how this also apply to our problem ?\nWe can **solve** our **complex problem** by solving **easier** ones first and build until we reach our complex problem. so we can calculate first the result for one pair then 2, 3, 4..... and build our table of solutions until we reach `n` pairs.\n\n---\n# Intuition\nFor now let\'s **assume** that we don\'t need the delivery to occur after its corresponding pickup.\nLet\'s start by **general** solution that we have `(n-1)` pairs and we want to find the number of combinations to **insert** the `n-th` pair\nif we looked at our image (where we assume n = 4 ) we can find that we have `(n-1) * 2` item and we can insert our two new items anywhere between them.\n\n\n\nFor our **first item** in `n-th` pair, we have `(n * 2 - 1)` new places to replace our new item.\nFor our **second item** in `n-th` pair, we have `(n * 2)` places to replace it. **Remember** that we already replaced the first item in the pair in it. \nSo from this places, we can conclude that we have `(n * 2 - 1) * n * 2` places to replace our two new items. \n\nLet\'s now **forget our assumption** that we talked about before, since we only need the pickup to occur **before** its corresponding delivery. Since the order matters here such that the **pickup** must occur **before** its **delivery** so half of our combinations are unacceptable -the combinations that the pickup will occur after its delivery- and the other half is our desired solution -the combinations that the pickup will occur before its delivery-.\n\nAccording to that, we will **divide our formula by two** and we will have `(n * 2 - 1) * n` number of ways to insert our `n-th` pair and we will calculate our **final solution** by **multiplying** the number of combinations to insert every `n-th` pair into the `n-1 th` pair starting from `1` going up to `n`. \n\n\n\n\n---\n\n\n# Proposed Solutions\n## 1. Recursive Approach (Top-Down)\n### Approach\n- Create a memoization vector to store computed values.\n- Recursive Function **calculateOrdersCount:**\n - Calculate the number of valid orders for remainingPairs using recursion and memoization.\n - **Base case**: If remainingPairs is 0, return 1.\n - Otherwise, calculate it using the formula `(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % MOD` and memoize the result.\n \n- Main Function **countOrders**:\n - **Initialize** memoization with -1 values.\n - Call **calculateOrdersCount** with numPairs to find the count of valid orders.\n - **Return** Result.\n\n### Complexity\n- **Time complexity:** $$O(N)$$\nWe are calculating the number of combinations for all pairs from n until we reach 1, so time complexity is `O(N)`.\n\n- **Space complexity:** $$O(N)$$\nWe are storing the array we are using for dynamic programming with size `n` and we are making recursive call with depth maximum `n` which is `2*N` space, so space complexity is `O(N)`.\n\n## 2. Iterative Approach (Bottom-Up)\n### Approach\n- Create a memoization array dp of size `numberOfPairs + 1`.\n- **Base Case:** Set dp[0] to 1, representing the one way to arrange 0 pairs.\n- Calculate Valid Orders **Iteratively**\n - Loop from 1 to numberOfPairs inclusive.\n - For each value of currentPairs, calculate dp[currentPairs] using the formula: `dp[currentPairs] = dp[currentPairs - 1] * (2 * currentPairs - 1) * currentPairs % MOD`.\n- **Return** Result.\n\n### Complexity\n- **Time complexity:** $$O(N)$$\nWe are calculating the number of combinations for all pairs from 1 until we reach n, so time complexity is `O(N)`\n\n- **Space complexity:** $$O(N)$$\nWe are storing the array we are using for dynamic programming with size `n`, so space complexity is `O(N)`.\n\n---\n\n\n# Code\n## 1. Recursive Approach (Top-Down)\n```C++ []\nclass Solution {\npublic:\n const int MOD = 1e9 + 7; // Modulus for calculations\n vector<long long> memoization; // Memoization array to store computed values\n\n long long calculateOrdersCount(long long remainingPairs) {\n // Base case: No remaining pairs, return 1\n if (remainingPairs == 0)\n return 1;\n\n // Check if the value is already computed and return it\n if (memoization[remainingPairs] != -1)\n return memoization[remainingPairs];\n\n // Calculate the number of valid orders for the remaining pairs\n long long currentResult = calculateOrdersCount(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % MOD;\n\n // Store the result in the memoization array and return it\n return memoization[remainingPairs] = currentResult;\n }\n\n int countOrders(int numPairs) {\n // Initialize the memoization array with -1 values\n memoization.resize(numPairs + 1, -1);\n\n // Calculate and return the count of valid orders\n return calculateOrdersCount(numPairs);\n }\n};\n```\n```Java []\nclass Solution {\n\n private int MOD = (int)1e9 + 7; // Modulus for calculations\n private static final int MAX_PAIRS = 510; // Maximum possible pairs value\n private long[] memoization = new long[MAX_PAIRS]; // Memoization array to store computed values\n\n private long calculateOrdersCount(long remainingPairs) {\n // Base case: No remaining pairs, return 1\n if (remainingPairs == 0)\n return 1;\n\n // Check if the value is already computed and return it\n if (memoization[(int)remainingPairs] != -1)\n return memoization[(int)remainingPairs];\n\n // Calculate the number of valid orders for the remaining pairs\n long currentResult = calculateOrdersCount(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % MOD;\n\n // Store the result in the memoization array and return it\n return memoization[(int)remainingPairs] = currentResult;\n }\n\n public int countOrders(int numPairs) {\n // Initialize the memoization array with -1 values\n for(int i = 0 ; i < numPairs + 5 ; i ++){\n memoization[i] = -1 ;\n }\n\n // Calculate and return the count of valid orders\n return (int)calculateOrdersCount(numPairs);\n }\n}\n```\n```Python []\nclass Solution:\n def __init__(self):\n self.MOD = int(1e9 + 7) # Modulus for calculations\n self.memoization = [] # Memoization array to store computed values\n\n def calculateOrdersCount(self, remainingPairs):\n # Base case: No remaining pairs, return 1\n if remainingPairs == 0:\n return 1\n\n # Check if the value is already computed and return it\n if self.memoization[remainingPairs] != -1:\n return self.memoization[remainingPairs]\n\n # Calculate the number of valid orders for the remaining pairs\n currentResult = self.calculateOrdersCount(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % self.MOD\n\n # Store the result in the memoization array and return it\n self.memoization[remainingPairs] = currentResult\n return currentResult\n\n def countOrders(self, numPairs):\n # Initialize the memoization array with -1 values\n self.memoization = [-1] * (numPairs + 1)\n\n # Calculate and return the count of valid orders\n return self.calculateOrdersCount(numPairs)\n```\n\n## 2. Iterative Approach (Bottom-Up) \n```C++ []\nclass Solution {\npublic:\n const int MOD = 1e9 + 7; // Modulus for calculations\n vector<long long> dp; // Array for memoization\n\n int countOrders(int numberOfPairs) {\n dp.resize(numberOfPairs + 1); // Initialize memoization array\n\n // Base case: there is one way to arrange 0 pairs\n dp[0] = 1;\n\n // Iterate over all values of pairs from 1 to n\n for (int currentPairs = 1; currentPairs <= numberOfPairs; currentPairs++) {\n // Calculate the number of valid orders for the current number of pairs\n dp[currentPairs] = dp[currentPairs - 1] * (2 * currentPairs - 1) * currentPairs % MOD;\n }\n\n return dp[numberOfPairs]; // Return the result for n pairs\n }\n};\n```\n```Java []\nclass Solution {\n\n private int MOD = (int)1e9 + 7; // Modulus for calculations\n\n public int countOrders(int numPairs) {\n // Memoization array to store computed values\n long[] dp = new long[numPairs + 1];\n\n // Base case: there is one way to arrange 0 pairs\n dp[0] = 1;\n\n // Iterate over all values of pairs from 1 to n\n for (int currentPairs = 1; currentPairs <= numPairs; currentPairs++) {\n // Calculate the number of valid orders for the current number of pairs\n dp[currentPairs] = dp[currentPairs - 1] * (2 * currentPairs - 1) * currentPairs % MOD;\n }\n\n return (int)dp[numPairs]; // Return the result for n pairs\n }\n}\n```\n```Python []\nclass Solution:\n def countOrders(self, numPairs: int) -> int:\n MOD = int(1e9 + 7) # Modulus for calculations\n MAX_PAIRS = numPairs + 1 # Maximum possible pairs value\n\n # Initialize the memoization array with -1 values\n dp = [0] * MAX_PAIRS\n\n # Base case: there is one way to arrange 0 pairs\n dp[0] = 1\n\n # Iterate over all values of pairs from 1 to n\n for currentPairs in range(1, numPairs + 1) :\n # Calculate the number of valid orders for the current number of pairs\n dp[currentPairs] = dp[currentPairs - 1] * (2 * currentPairs - 1) * currentPairs % MOD;\n\n # Return the result for n pairs\n return dp[numPairs]; \n```\n\n\n---\n\n\n# No need of DP array?\nYes, in the proposed approaches -Recursive and Iterative-, we can only **use one variable** instead of using dp array to store all of the cases.\n\nIs using one variable instead of an array is **considered as DP** ?\n**Yes**, we can say that using one variable in considered as DP since it has the **core of DP** which is caching the results that we will use it later instead of re-calculate it again even if it was one variable.\n\nUsing one variable will only affect the **space complexity**:\n- In the **Recursive approach** instead of `2*N` it will only be `N` which is the depth of the recursive call stack so `O(N)`\n- In the **Iterative approach** it will be `O(1)` since we only storing one variable without recursive calls.\n\n\n## Code\n## 1. Recursive Approach (Top-Down)\n```C++ []\nclass Solution {\n public:\n int MOD = (int)1e9 + 7; // Modulus for calculations\n\n long long calculateOrdersCount(long long remainingPairs) {\n // Base case: No remaining pairs, return 1\n if (remainingPairs == 0)\n return 1;\n\n // Calculate the number of valid orders for the remaining pairs\n long long currentResult = calculateOrdersCount(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % MOD;\n\n return currentResult;\n }\n\n int countOrders(int numPairs) {\n // Calculate and return the count of valid orders\n return calculateOrdersCount(numPairs);\n }\n};\n```\n```Java []\nclass Solution {\n\n private int MOD = (int)1e9 + 7; // Modulus for calculations\n\n private long calculateOrdersCount(long remainingPairs) {\n // Base case: No remaining pairs, return 1\n if (remainingPairs == 0)\n return 1;\n\n // Calculate the number of valid orders for the remaining pairs\n long currentResult = calculateOrdersCount(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % MOD;\n\n return currentResult;\n }\n\n public int countOrders(int numPairs) {\n // Calculate and return the count of valid orders\n return (int)calculateOrdersCount(numPairs);\n }\n}\n```\n```Python []\nclass Solution:\n def __init__(self):\n self.MOD = int(1e9 + 7) # Modulus for calculations\n\n def calculateOrdersCount(self, remainingPairs):\n # Base case: No remaining pairs, return 1\n if remainingPairs == 0:\n return 1\n\n # Calculate the number of valid orders for the remaining pairs\n currentResult = self.calculateOrdersCount(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % self.MOD\n\n return currentResult\n\n def countOrders(self, numPairs):\n # Calculate and return the count of valid orders\n return self.calculateOrdersCount(numPairs)\n```\n\n## 2. Iterative Approach (Bottom-Up) \n```C++ []\nclass Solution {\npublic:\n const int MOD = 1e9 + 7; // Modulus for calculations\n\n int countOrders(int numberOfPairs) {\n long long count = 1 ;\n\n // Iterate over all values of pairs from 1 to n\n for (int currentPairs = 1; currentPairs <= numberOfPairs; currentPairs++) {\n // Calculate the number of valid orders for the current number of pairs\n count = count * (2 * currentPairs - 1) * currentPairs % MOD;\n }\n\n return count; // Return the result for n pairs\n }\n};\n```\n```Java []\nclass Solution {\n private int MOD = (int)1e9 + 7; // Modulus for calculations\n\n public int countOrders(int numberOfPairs) {\n long count = 1 ;\n\n // Iterate over all values of pairs from 1 to n\n for (int currentPairs = 1; currentPairs <= numberOfPairs; currentPairs++) {\n // Calculate the number of valid orders for the current number of pairs\n count = count * (2 * currentPairs - 1) * currentPairs % MOD;\n }\n\n return (int)count; // Return the result for n pairs\n }\n};\n```\n```Python []\nclass Solution:\n def countOrders(self, numPairs: int) -> int:\n MOD = int(1e9 + 7) # Modulus for calculations\n\n count = 1\n\n # Iterate over all values of pairs from 1 to n\n for currentPairs in range(1, numPairs + 1) :\n # Calculate the number of valid orders for the current number of pairs\n count = count * (2 * currentPairs - 1) * currentPairs % MOD;\n\n # Return the result for n pairs\n return count; \n```\n\n\n\n\n\n\n | 62 | Given a binary string `s` and an integer `k`, return `true` _if every binary code of length_ `k` _is a substring of_ `s`. Otherwise, return `false`.
**Example 1:**
**Input:** s = "00110110 ", k = 2
**Output:** true
**Explanation:** The binary codes of length 2 are "00 ", "01 ", "10 " and "11 ". They can be all found as substrings at indices 0, 1, 3 and 2 respectively.
**Example 2:**
**Input:** s = "0110 ", k = 1
**Output:** true
**Explanation:** The binary codes of length 1 are "0 " and "1 ", it is clear that both exist as a substring.
**Example 3:**
**Input:** s = "0110 ", k = 2
**Output:** false
**Explanation:** The binary code "00 " is of length 2 and does not exist in the array.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= k <= 20` | Use the permutation and combination theory to add one (P, D) pair each time until n pairs. |
A solution you shouldn't read. | count-all-valid-pickup-and-delivery-options | 0 | 1 | # Intuition\nNO intuition at all ppl\n# Approach\nGuessing.\n# Complexity\n- Time complexity:\nO(1) this is as fast as it can get. Assuming python can do the factorial and the power in O(1) which is not the case.\n- Space complexity:\nO(1)\n# Code\n```\nclass Solution:\n def countOrders(self, n: int) -> int:\n\n return (factorial(2*n)//2**n) % (10**9 + 7)\n \n\n\n``` | 1 | Given `n` orders, each order consist in pickup and delivery services.
Count all valid pickup/delivery possible sequences such that delivery(i) is always after of pickup(i).
Since the answer may be too large, return it modulo 10^9 + 7.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation:** Unique order (P1, D1), Delivery 1 always is after of Pickup 1.
**Example 2:**
**Input:** n = 2
**Output:** 6
**Explanation:** All possible orders:
(P1,P2,D1,D2), (P1,P2,D2,D1), (P1,D1,P2,D2), (P2,P1,D1,D2), (P2,P1,D2,D1) and (P2,D2,P1,D1).
This is an invalid order (P1,D2,P2,D1) because Pickup 2 is after of Delivery 2.
**Example 3:**
**Input:** n = 3
**Output:** 90
**Constraints:**
* `1 <= n <= 500`
Given 2 integers n and start. Your task is return any permutation p of (0,1,2.....,2^n -1) such that : p\[0\] = start, p\[i\] and p\[i+1\] differ by only one bit for all 0 <= i < 2^n - 1. | Use gray code to generate a n-bit sequence. Rotate the sequence such that its first element is start. |
A solution you shouldn't read. | count-all-valid-pickup-and-delivery-options | 0 | 1 | # Intuition\nNO intuition at all ppl\n# Approach\nGuessing.\n# Complexity\n- Time complexity:\nO(1) this is as fast as it can get. Assuming python can do the factorial and the power in O(1) which is not the case.\n- Space complexity:\nO(1)\n# Code\n```\nclass Solution:\n def countOrders(self, n: int) -> int:\n\n return (factorial(2*n)//2**n) % (10**9 + 7)\n \n\n\n``` | 1 | Given a binary string `s` and an integer `k`, return `true` _if every binary code of length_ `k` _is a substring of_ `s`. Otherwise, return `false`.
**Example 1:**
**Input:** s = "00110110 ", k = 2
**Output:** true
**Explanation:** The binary codes of length 2 are "00 ", "01 ", "10 " and "11 ". They can be all found as substrings at indices 0, 1, 3 and 2 respectively.
**Example 2:**
**Input:** s = "0110 ", k = 1
**Output:** true
**Explanation:** The binary codes of length 1 are "0 " and "1 ", it is clear that both exist as a substring.
**Example 3:**
**Input:** s = "0110 ", k = 2
**Output:** false
**Explanation:** The binary code "00 " is of length 2 and does not exist in the array.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= k <= 20` | Use the permutation and combination theory to add one (P, D) pair each time until n pairs. |
simple One liner python easy to understand | count-all-valid-pickup-and-delivery-options | 0 | 1 | # Code\n```python\nclass Solution:\n def countOrders(self, n: int) -> int:\n return (factorial(2*n) // (2**n)) % (10**9 + 7)\n \n \n``` | 1 | Given `n` orders, each order consist in pickup and delivery services.
Count all valid pickup/delivery possible sequences such that delivery(i) is always after of pickup(i).
Since the answer may be too large, return it modulo 10^9 + 7.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation:** Unique order (P1, D1), Delivery 1 always is after of Pickup 1.
**Example 2:**
**Input:** n = 2
**Output:** 6
**Explanation:** All possible orders:
(P1,P2,D1,D2), (P1,P2,D2,D1), (P1,D1,P2,D2), (P2,P1,D1,D2), (P2,P1,D2,D1) and (P2,D2,P1,D1).
This is an invalid order (P1,D2,P2,D1) because Pickup 2 is after of Delivery 2.
**Example 3:**
**Input:** n = 3
**Output:** 90
**Constraints:**
* `1 <= n <= 500`
Given 2 integers n and start. Your task is return any permutation p of (0,1,2.....,2^n -1) such that : p\[0\] = start, p\[i\] and p\[i+1\] differ by only one bit for all 0 <= i < 2^n - 1. | Use gray code to generate a n-bit sequence. Rotate the sequence such that its first element is start. |
simple One liner python easy to understand | count-all-valid-pickup-and-delivery-options | 0 | 1 | # Code\n```python\nclass Solution:\n def countOrders(self, n: int) -> int:\n return (factorial(2*n) // (2**n)) % (10**9 + 7)\n \n \n``` | 1 | Given a binary string `s` and an integer `k`, return `true` _if every binary code of length_ `k` _is a substring of_ `s`. Otherwise, return `false`.
**Example 1:**
**Input:** s = "00110110 ", k = 2
**Output:** true
**Explanation:** The binary codes of length 2 are "00 ", "01 ", "10 " and "11 ". They can be all found as substrings at indices 0, 1, 3 and 2 respectively.
**Example 2:**
**Input:** s = "0110 ", k = 1
**Output:** true
**Explanation:** The binary codes of length 1 are "0 " and "1 ", it is clear that both exist as a substring.
**Example 3:**
**Input:** s = "0110 ", k = 2
**Output:** false
**Explanation:** The binary code "00 " is of length 2 and does not exist in the array.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= k <= 20` | Use the permutation and combination theory to add one (P, D) pair each time until n pairs. |
Easy solution || Python | count-all-valid-pickup-and-delivery-options | 0 | 1 | # Approach\nThe formula seems to be based on the observation that for each additional order, you have two choices for the pickup and delivery locations: you can either insert the pickup and its corresponding delivery at the beginning or insert them at the end of the existing sequence. The `(2*i-1)*i` term represents the number of ways to arrange the pickup and delivery within the current sequence of `i` orders.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def countOrders(self, n: int) -> int:\n dp = [0] * (n+1)\n MOD=10**9+7\n dp[0]=1\n dp[1]=1\n if n>=2:\n for i in range(2,n+1):\n dp[i]= (dp[i-1]* (2*i-1)*i) % MOD\n return dp[n]\n \n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79** | 1 | Given `n` orders, each order consist in pickup and delivery services.
Count all valid pickup/delivery possible sequences such that delivery(i) is always after of pickup(i).
Since the answer may be too large, return it modulo 10^9 + 7.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation:** Unique order (P1, D1), Delivery 1 always is after of Pickup 1.
**Example 2:**
**Input:** n = 2
**Output:** 6
**Explanation:** All possible orders:
(P1,P2,D1,D2), (P1,P2,D2,D1), (P1,D1,P2,D2), (P2,P1,D1,D2), (P2,P1,D2,D1) and (P2,D2,P1,D1).
This is an invalid order (P1,D2,P2,D1) because Pickup 2 is after of Delivery 2.
**Example 3:**
**Input:** n = 3
**Output:** 90
**Constraints:**
* `1 <= n <= 500`
Given 2 integers n and start. Your task is return any permutation p of (0,1,2.....,2^n -1) such that : p\[0\] = start, p\[i\] and p\[i+1\] differ by only one bit for all 0 <= i < 2^n - 1. | Use gray code to generate a n-bit sequence. Rotate the sequence such that its first element is start. |
Easy solution || Python | count-all-valid-pickup-and-delivery-options | 0 | 1 | # Approach\nThe formula seems to be based on the observation that for each additional order, you have two choices for the pickup and delivery locations: you can either insert the pickup and its corresponding delivery at the beginning or insert them at the end of the existing sequence. The `(2*i-1)*i` term represents the number of ways to arrange the pickup and delivery within the current sequence of `i` orders.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def countOrders(self, n: int) -> int:\n dp = [0] * (n+1)\n MOD=10**9+7\n dp[0]=1\n dp[1]=1\n if n>=2:\n for i in range(2,n+1):\n dp[i]= (dp[i-1]* (2*i-1)*i) % MOD\n return dp[n]\n \n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79** | 1 | Given a binary string `s` and an integer `k`, return `true` _if every binary code of length_ `k` _is a substring of_ `s`. Otherwise, return `false`.
**Example 1:**
**Input:** s = "00110110 ", k = 2
**Output:** true
**Explanation:** The binary codes of length 2 are "00 ", "01 ", "10 " and "11 ". They can be all found as substrings at indices 0, 1, 3 and 2 respectively.
**Example 2:**
**Input:** s = "0110 ", k = 1
**Output:** true
**Explanation:** The binary codes of length 1 are "0 " and "1 ", it is clear that both exist as a substring.
**Example 3:**
**Input:** s = "0110 ", k = 2
**Output:** false
**Explanation:** The binary code "00 " is of length 2 and does not exist in the array.
**Constraints:**
* `1 <= s.length <= 5 * 105`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= k <= 20` | Use the permutation and combination theory to add one (P, D) pair each time until n pairs. |
Python solution ( using datetime ) | number-of-days-between-two-dates | 0 | 1 | ```\nfrom datetime import datetime\n\nclass Solution:\n def daysBetweenDates(self, date1: str, date2: str) -> int:\n a: list(int) = [int(number) for number in date1.split("-")]\n b: list(int) = [int(number) for number in date2.split("-")]\n\n a: float = datetime(*a).timestamp()\n b: float = datetime(*b).timestamp()\n\n return int(abs(a - b) / 86400)\n```\n\n\n## No modules\n```\nclass Solution:\n def daysBetweenDates(self, date1: str, date2: str) -> int:\n def is_leap_year(year) -> bool:\n return (year % 4 == 0 and year % 100 != 0) or (year % 400 == 0)\n \n def get_days(date: str) -> int:\n days_in_month: dict[int, int] = {\n 1: 31,\n 2: 28, # This value might be 29 for leap years\n 3: 31,\n 4: 30,\n 5: 31,\n 6: 30,\n 7: 31,\n 8: 31,\n 9: 30,\n 10: 31,\n 11: 30,\n 12: 31,\n }\n year, month, days = [int(number) for number in date.split("-")]\n\n if is_leap_year(year): days_in_month[2] = 29\n \n total: int = 0\n \n for year in range(1971, year):\n if is_leap_year(year): total += 366\n else: total += 365\n \n for month in range(1, month):\n total += days_in_month[month]\n\n total += days\n\n return total\n return abs(get_days(date1) - get_days(date2))\n``` | 1 | Write a program to count the number of days between two dates.
The two dates are given as strings, their format is `YYYY-MM-DD` as shown in the examples.
**Example 1:**
**Input:** date1 = "2019-06-29", date2 = "2019-06-30"
**Output:** 1
**Example 2:**
**Input:** date1 = "2020-01-15", date2 = "2019-12-31"
**Output:** 15
**Constraints:**
* The given dates are valid dates between the years `1971` and `2100`. | You can try all combinations and keep mask of characters you have. You can use DP. |
Python easy.. but I got 茴字有3种写法 | number-of-days-between-two-dates | 0 | 1 | # Intuition\n\u8334\u5B57\u67093\u79CD\u5199\u6CD5\n\n# Code\n```\n def daysBetweenDates(self, date1: str, date2: str) -> int:\n \n y,m,d = date1.split("-")\n date_format = "%Y-%m-%d"\n\n a = datetime.datetime.strptime(date1, date_format)\n b = datetime.datetime.strptime(date2, date_format)\n\n return abs((b - a).days)\n```\n```\n def daysBetweenDates(self, date1: str, date2: str) -> int:\n\n d1 = [int(x) for x in date1.split("-")]\n d2 = [int(x) for x in date2.split("-")]\n\n d1 = date(d1[0], d1[1], d1[2])\n d2 = date(d2[0], d2[1], d2[2])\n\n return abs((d1-d2).days)\n```\n```\n def daysBetweenDates(self, date1: str, date2: str) -> int:\n\n days = list(accumulate([0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30]))\n is_leap = lambda year: year % 4 == 0 and (year % 100 != 0 or year % 400 == 0)\n\n def from71(da):\n y, m, d = da.split("-")\n y, m, d = int(y), int(m), int(d)\n\n ans = d + int(m>2 and is_leap(y))\n ans += days[m-1]\n ans += sum(365 + int(is_leap(y)) for y in range(1971, y))\n return ans\n \n return abs(from71(date1)- from71(date2))\n\n\n\n\n\n``` | 1 | Write a program to count the number of days between two dates.
The two dates are given as strings, their format is `YYYY-MM-DD` as shown in the examples.
**Example 1:**
**Input:** date1 = "2019-06-29", date2 = "2019-06-30"
**Output:** 1
**Example 2:**
**Input:** date1 = "2020-01-15", date2 = "2019-12-31"
**Output:** 15
**Constraints:**
* The given dates are valid dates between the years `1971` and `2100`. | You can try all combinations and keep mask of characters you have. You can use DP. |
Simple & Easy Solution by Python 3 | number-of-days-between-two-dates | 0 | 1 | ```\nclass Solution:\n def daysBetweenDates(self, date1: str, date2: str) -> int:\n def is_leap_year(year: int) -> bool:\n return year % 4 == 0 and (year % 100 != 0 or year % 400 == 0)\n\n def get_days(date: str) -> int:\n y, m, d = map(int, date.split(\'-\'))\n\n days = d + int(is_leap_year(y) and m > 2)\n days += sum(365 + int(is_leap_year(y)) for y in range(1971, y))\n days += sum([0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31][:m])\n\n return days\n\n return abs(get_days(date1) - get_days(date2))\n``` | 13 | Write a program to count the number of days between two dates.
The two dates are given as strings, their format is `YYYY-MM-DD` as shown in the examples.
**Example 1:**
**Input:** date1 = "2019-06-29", date2 = "2019-06-30"
**Output:** 1
**Example 2:**
**Input:** date1 = "2020-01-15", date2 = "2019-12-31"
**Output:** 15
**Constraints:**
* The given dates are valid dates between the years `1971` and `2100`. | You can try all combinations and keep mask of characters you have. You can use DP. |
Python 3 - One Liner Using DATETIME | number-of-days-between-two-dates | 0 | 1 | Approach:\n1. The input is of type <```string```>. To use the datetime module, these strings will first be converted into type <```date```> using ```datetime.strptime(date_string, format)```.\n2. After conversion, the dates are subtracted, i.e. ```(date2 - date1).days()```\n\nNote:\n```abs()``` must be used when calculating the difference as any of the dates could be bigger than the other.\n\n```\nfrom datetime import datetime\nclass Solution:\n def daysBetweenDates(self, date1: str, date2: str) -> int:\n return abs((datetime.strptime(date2, \'%Y-%m-%d\').date() - datetime.strptime(date1, \'%Y-%m-%d\').date()).days)\n```\n<br>**Cleaner Version:**\n```\nfrom datetime import datetime\nclass Solution:\n def daysBetweenDates(self, date1: str, date2: str) -> int:\n M = datetime.strptime(date1, \'%Y-%m-%d\').date()\n N = datetime.strptime(date2, \'%Y-%m-%d\').date()\n return abs((N - M).days)\n``` | 16 | Write a program to count the number of days between two dates.
The two dates are given as strings, their format is `YYYY-MM-DD` as shown in the examples.
**Example 1:**
**Input:** date1 = "2019-06-29", date2 = "2019-06-30"
**Output:** 1
**Example 2:**
**Input:** date1 = "2020-01-15", date2 = "2019-12-31"
**Output:** 15
**Constraints:**
* The given dates are valid dates between the years `1971` and `2100`. | You can try all combinations and keep mask of characters you have. You can use DP. |
Python3 Datetime approach | number-of-days-between-two-dates | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDatetime\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom datetime import datetime\nclass Solution:\n def daysBetweenDates(self, date1: str, date2: str) -> int:\n x = datetime.strptime(date1, \'%Y-%m-%d\')\n y = datetime.strptime(date2, \'%Y-%m-%d\')\n return abs((y - x).days)\n``` | 2 | Write a program to count the number of days between two dates.
The two dates are given as strings, their format is `YYYY-MM-DD` as shown in the examples.
**Example 1:**
**Input:** date1 = "2019-06-29", date2 = "2019-06-30"
**Output:** 1
**Example 2:**
**Input:** date1 = "2020-01-15", date2 = "2019-12-31"
**Output:** 15
**Constraints:**
* The given dates are valid dates between the years `1971` and `2100`. | You can try all combinations and keep mask of characters you have. You can use DP. |
Python3 Solution from Scratch - NOT USING DATETIME | number-of-days-between-two-dates | 0 | 1 | ```\nclass Solution:\n def daysBetweenDates(self, date1: str, date2: str) -> int:\n \n def f_date(date): # calculates days passed since \'1900-01-01\'\n year0 = \'1900\'\n year1, month1, day1 = date.split(\'-\')\n \n days = 0\n for y in range(int(year0), int(year1)):\n days += 365\n if y%100 == 0:\n if y%400 == 0:\n days += 1\n else:\n if y%4 == 0:\n days += 1\n \n for m in range(int(month1)):\n if m in [1, 3, 5, 7, 8, 10, 12]:\n days += 31\n if m in [4, 6, 9, 11]:\n days += 30\n if m == 2:\n days += 28\n if int(year1)%100 == 0:\n if int(year1)%400 == 0:\n days += 1\n else:\n if int(year1)%4 ==0:\n days += 1\n days += int(day1)\n return days\n\t\t\t\n return abs(f_date(date1) - f_date(date2))\n``` | 4 | Write a program to count the number of days between two dates.
The two dates are given as strings, their format is `YYYY-MM-DD` as shown in the examples.
**Example 1:**
**Input:** date1 = "2019-06-29", date2 = "2019-06-30"
**Output:** 1
**Example 2:**
**Input:** date1 = "2020-01-15", date2 = "2019-12-31"
**Output:** 15
**Constraints:**
* The given dates are valid dates between the years `1971` and `2100`. | You can try all combinations and keep mask of characters you have. You can use DP. |
mySolution | number-of-days-between-two-dates | 0 | 1 | # Code\n```\nfrom datetime import datetime\nclass Solution:\n def daysBetweenDates(self, date1: str, date2: str) -> int:\n date_format = "%Y-%m-%d"\n return abs((datetime.strptime(date1, date_format)-datetime.strptime(date2,date_format)).days)\n``` | 0 | Write a program to count the number of days between two dates.
The two dates are given as strings, their format is `YYYY-MM-DD` as shown in the examples.
**Example 1:**
**Input:** date1 = "2019-06-29", date2 = "2019-06-30"
**Output:** 1
**Example 2:**
**Input:** date1 = "2020-01-15", date2 = "2019-12-31"
**Output:** 15
**Constraints:**
* The given dates are valid dates between the years `1971` and `2100`. | You can try all combinations and keep mask of characters you have. You can use DP. |
Number of days between two dates | number-of-days-between-two-dates | 0 | 1 | \n# Code\n```\nclass Solution:\n def daysBetweenDates(self, date1: str, date2: str) -> int:\n def isl(year):\n return (year% 4==0) and (year%100!=0) or (year%400==0)\n\n k = [0, 31, 59, 90, 120, 151, 181, 212, 243, 273, 304, 334, 365]\n\n y1, m1, d1 = map(int, date1.split("-"))\n y2, m2, d2 = map(int, date2.split("-"))\n\n if y1 > y2:\n y2, m2, d2, y1, m1, d1 = y1, m1, d1, y2, m2, d2 \n\n ans = d2 + (k[m2-1] - k[m1-1])\n for y in range(y1, y2, 1):\n ans += 366 if isl(y) else 365\n \n if (isl(y1) and m1>2):\n ans -= 1\n if (isl(y2) and m2>2):\n ans += 1\n\n return abs(ans-d1)\n``` | 0 | Write a program to count the number of days between two dates.
The two dates are given as strings, their format is `YYYY-MM-DD` as shown in the examples.
**Example 1:**
**Input:** date1 = "2019-06-29", date2 = "2019-06-30"
**Output:** 1
**Example 2:**
**Input:** date1 = "2020-01-15", date2 = "2019-12-31"
**Output:** 15
**Constraints:**
* The given dates are valid dates between the years `1971` and `2100`. | You can try all combinations and keep mask of characters you have. You can use DP. |
✅ 82.42% Easy BFS | validate-binary-tree-nodes | 1 | 1 | # Intuition\nInitially, we can observe that in a valid binary tree, there should be exactly one node with an in-degree of 0 (the root), and all other nodes should have an in-degree of 1. Furthermore, all nodes should be reachable from the root node. These observations form the basis of our approach to solving this problem.\n\n# Live Coding & Explaining\nhttps://youtu.be/PQDxL1v9BtM?si=3mwQUSma01CcKfSj\n\n# Approach\n1. **In-degree Calculation**: \n - We initialize an array `indegree` to keep track of the in-degree of each node. \n - We iterate through `leftChild` and `rightChild` arrays, incrementing the in-degree of the corresponding nodes.\n \n2. **Root Identification**:\n - We then iterate through the `indegree` array to identify the root node (a node with an in-degree of 0).\n - If we find more than one node with an in-degree of 0, or if we do not find any such node, we return `False` since the nodes do not form a valid binary tree.\n \n3. **Breadth-First Search (BFS)**:\n - Having identified the root, we perform a BFS traversal starting from the root to visit all nodes in the tree.\n - We use a queue to manage the BFS traversal, and a `visited` array to keep track of which nodes have been visited.\n - If we encounter a node that has already been visited, we return `False` as this indicates a cycle in the graph, which violates the tree property.\n \n4. **Validation**:\n - Finally, we validate that all nodes have been visited by comparing the sum of the `visited` array to `n`. If they are equal, it means all nodes were reachable from the root, and we return `True`. Otherwise, we return `False`.\n\n# Complexity\n- **Time complexity:**\n - In-degree calculation: $$O(n)$$\n - Root identification: $$O(n)$$\n - BFS traversal: $$O(n)$$\n - Validation: $$O(n)$$\n - Overall time complexity: $$O(n)$$\n\n- **Space complexity:**\n - The space complexity is dominated by the `indegree` and `visited` arrays, each of size $$O(n)$$, and the queue, which in the worst case can also be of size $$O(n)$$.\n - Overall space complexity: $$O(n)$$\n\n# Code\n``` Python []\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n indegree = [0] * n # Initialize in-degree of all nodes to 0\n \n # Build the in-degree array in a single pass\n for i in range(n):\n if leftChild[i] != -1:\n indegree[leftChild[i]] += 1\n if rightChild[i] != -1:\n indegree[rightChild[i]] += 1\n \n # Find the root (node with in-degree 0)\n root = None\n for i in range(n):\n if indegree[i] == 0:\n if root is None:\n root = i\n else:\n return False # More than one root\n \n # If there\'s no root\n if root is None:\n return False\n \n visited = [False] * n\n queue = deque([root])\n \n while queue:\n node = queue.popleft()\n if visited[node]:\n return False # Already visited this node, not a valid tree\n visited[node] = True\n if leftChild[node] != -1:\n queue.append(leftChild[node])\n if rightChild[node] != -1:\n queue.append(rightChild[node])\n \n return sum(visited) == n # If all nodes are visited, it\'s a valid tree\n```\n``` C++ []\nclass Solution {\npublic:\n bool validateBinaryTreeNodes(int n, std::vector<int>& leftChild, std::vector<int>& rightChild) {\n std::vector<int> indegree(n, 0);\n for (int i = 0; i < n; ++i) {\n if (leftChild[i] != -1) indegree[leftChild[i]]++;\n if (rightChild[i] != -1) indegree[rightChild[i]]++;\n }\n int root = -1;\n for (int i = 0; i < n; ++i) {\n if (indegree[i] == 0) {\n if (root == -1) root = i;\n else return false;\n }\n }\n if (root == -1) return false;\n std::vector<bool> visited(n, false);\n std::queue<int> queue;\n queue.push(root);\n while (!queue.empty()) {\n int node = queue.front(); queue.pop();\n if (visited[node]) return false;\n visited[node] = true;\n if (leftChild[node] != -1) queue.push(leftChild[node]);\n if (rightChild[node] != -1) queue.push(rightChild[node]);\n }\n return std::accumulate(visited.begin(), visited.end(), 0) == n;\n }\n};\n```\n``` Java []\nclass Solution {\n public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {\n int[] indegree = new int[n];\n for (int i = 0; i < n; i++) {\n if (leftChild[i] != -1) indegree[leftChild[i]]++;\n if (rightChild[i] != -1) indegree[rightChild[i]]++;\n }\n int root = -1;\n for (int i = 0; i < n; i++) {\n if (indegree[i] == 0) {\n if (root == -1) root = i;\n else return false;\n }\n }\n if (root == -1) return false;\n boolean[] visited = new boolean[n];\n Queue<Integer> queue = new LinkedList<>();\n queue.offer(root);\n while (!queue.isEmpty()) {\n int node = queue.poll();\n if (visited[node]) return false;\n visited[node] = true;\n if (leftChild[node] != -1) queue.offer(leftChild[node]);\n if (rightChild[node] != -1) queue.offer(rightChild[node]);\n }\n int trueCount = 0;\n for (boolean b : visited) {\n if (b) trueCount++;\n }\n return trueCount == n;\n\n }\n}\n```\n | 50 | You have `n` binary tree nodes numbered from `0` to `n - 1` where node `i` has two children `leftChild[i]` and `rightChild[i]`, return `true` if and only if **all** the given nodes form **exactly one** valid binary tree.
If node `i` has no left child then `leftChild[i]` will equal `-1`, similarly for the right child.
Note that the nodes have no values and that we only use the node numbers in this problem.
**Example 1:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,-1,-1,-1\]
**Output:** true
**Example 2:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,3,-1,-1\]
**Output:** false
**Example 3:**
**Input:** n = 2, leftChild = \[1,0\], rightChild = \[-1,-1\]
**Output:** false
**Constraints:**
* `n == leftChild.length == rightChild.length`
* `1 <= n <= 104`
* `-1 <= leftChild[i], rightChild[i] <= n - 1` | Can you use backtracking to solve this problem ?. Suppose you've placed a bunch of squares. Where is the natural spot to place the next square ?. The maximum number of squares to be placed will be ≤ max(n,m). |
✅ 82.42% Easy BFS | validate-binary-tree-nodes | 1 | 1 | # Intuition\nInitially, we can observe that in a valid binary tree, there should be exactly one node with an in-degree of 0 (the root), and all other nodes should have an in-degree of 1. Furthermore, all nodes should be reachable from the root node. These observations form the basis of our approach to solving this problem.\n\n# Live Coding & Explaining\nhttps://youtu.be/PQDxL1v9BtM?si=3mwQUSma01CcKfSj\n\n# Approach\n1. **In-degree Calculation**: \n - We initialize an array `indegree` to keep track of the in-degree of each node. \n - We iterate through `leftChild` and `rightChild` arrays, incrementing the in-degree of the corresponding nodes.\n \n2. **Root Identification**:\n - We then iterate through the `indegree` array to identify the root node (a node with an in-degree of 0).\n - If we find more than one node with an in-degree of 0, or if we do not find any such node, we return `False` since the nodes do not form a valid binary tree.\n \n3. **Breadth-First Search (BFS)**:\n - Having identified the root, we perform a BFS traversal starting from the root to visit all nodes in the tree.\n - We use a queue to manage the BFS traversal, and a `visited` array to keep track of which nodes have been visited.\n - If we encounter a node that has already been visited, we return `False` as this indicates a cycle in the graph, which violates the tree property.\n \n4. **Validation**:\n - Finally, we validate that all nodes have been visited by comparing the sum of the `visited` array to `n`. If they are equal, it means all nodes were reachable from the root, and we return `True`. Otherwise, we return `False`.\n\n# Complexity\n- **Time complexity:**\n - In-degree calculation: $$O(n)$$\n - Root identification: $$O(n)$$\n - BFS traversal: $$O(n)$$\n - Validation: $$O(n)$$\n - Overall time complexity: $$O(n)$$\n\n- **Space complexity:**\n - The space complexity is dominated by the `indegree` and `visited` arrays, each of size $$O(n)$$, and the queue, which in the worst case can also be of size $$O(n)$$.\n - Overall space complexity: $$O(n)$$\n\n# Code\n``` Python []\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n indegree = [0] * n # Initialize in-degree of all nodes to 0\n \n # Build the in-degree array in a single pass\n for i in range(n):\n if leftChild[i] != -1:\n indegree[leftChild[i]] += 1\n if rightChild[i] != -1:\n indegree[rightChild[i]] += 1\n \n # Find the root (node with in-degree 0)\n root = None\n for i in range(n):\n if indegree[i] == 0:\n if root is None:\n root = i\n else:\n return False # More than one root\n \n # If there\'s no root\n if root is None:\n return False\n \n visited = [False] * n\n queue = deque([root])\n \n while queue:\n node = queue.popleft()\n if visited[node]:\n return False # Already visited this node, not a valid tree\n visited[node] = True\n if leftChild[node] != -1:\n queue.append(leftChild[node])\n if rightChild[node] != -1:\n queue.append(rightChild[node])\n \n return sum(visited) == n # If all nodes are visited, it\'s a valid tree\n```\n``` C++ []\nclass Solution {\npublic:\n bool validateBinaryTreeNodes(int n, std::vector<int>& leftChild, std::vector<int>& rightChild) {\n std::vector<int> indegree(n, 0);\n for (int i = 0; i < n; ++i) {\n if (leftChild[i] != -1) indegree[leftChild[i]]++;\n if (rightChild[i] != -1) indegree[rightChild[i]]++;\n }\n int root = -1;\n for (int i = 0; i < n; ++i) {\n if (indegree[i] == 0) {\n if (root == -1) root = i;\n else return false;\n }\n }\n if (root == -1) return false;\n std::vector<bool> visited(n, false);\n std::queue<int> queue;\n queue.push(root);\n while (!queue.empty()) {\n int node = queue.front(); queue.pop();\n if (visited[node]) return false;\n visited[node] = true;\n if (leftChild[node] != -1) queue.push(leftChild[node]);\n if (rightChild[node] != -1) queue.push(rightChild[node]);\n }\n return std::accumulate(visited.begin(), visited.end(), 0) == n;\n }\n};\n```\n``` Java []\nclass Solution {\n public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {\n int[] indegree = new int[n];\n for (int i = 0; i < n; i++) {\n if (leftChild[i] != -1) indegree[leftChild[i]]++;\n if (rightChild[i] != -1) indegree[rightChild[i]]++;\n }\n int root = -1;\n for (int i = 0; i < n; i++) {\n if (indegree[i] == 0) {\n if (root == -1) root = i;\n else return false;\n }\n }\n if (root == -1) return false;\n boolean[] visited = new boolean[n];\n Queue<Integer> queue = new LinkedList<>();\n queue.offer(root);\n while (!queue.isEmpty()) {\n int node = queue.poll();\n if (visited[node]) return false;\n visited[node] = true;\n if (leftChild[node] != -1) queue.offer(leftChild[node]);\n if (rightChild[node] != -1) queue.offer(rightChild[node]);\n }\n int trueCount = 0;\n for (boolean b : visited) {\n if (b) trueCount++;\n }\n return trueCount == n;\n\n }\n}\n```\n | 50 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
🚀 93.31% || BFS & DFS || Explained Intuition🚀 | validate-binary-tree-nodes | 1 | 1 | # Porblem Description\n\nGiven `n` binary tree nodes numbered from `0` to `n - 1`, represented by arrays `leftChild` and `rightChild` where each element corresponds to the `left` and `right` child of a node respectively, **determine** if the provided nodes **form** exactly one **valid** binary tree. \nA node with **no left** child is represented by `-1` in the `leftChild` array, and **similarly** for a node with **no right** child in the `rightChild` array. \nThe **goal** is to verify if the given nodes, identified solely by their numbers, constitute a **valid** binary tree structure.\n\n- **Constraints:**\n - `n == leftChild.length == rightChild.length`\n - `1 <= n <= 10e4`\n - `-1 <= leftChild[i], rightChild[i] <= n - 1`\n\n\n---\n\n# Intuition\n\nHi there, \uD83D\uDE03\n\nLet\'s deep dive\uD83E\uDD3F in our today\'s Interesting problem.\nThe goal in our ptoblem is to **validate** if a given nodes can form a **valid Binary Tree Structure**\uD83C\uDF32.\n\nBut what is the structure of a binary tree\u2753\n- Simply:\n - Each node has only **one parent** (Except for the root).\n - There is only **one root**.\n - Each node has at most **2 children** (leaf nodes have no children).\n - There is **no Cycle**.\uD83D\uDEB4\u200D\u2640\uFE0F\n\nSeems Valid \u2714\nLet\'s take a look at these trees\uD83C\uDF32\uD83C\uDF33.\n\nThis is **invalid** Binary Tree, Why?\uD83E\uDD14\nnode `4` have `2` parents which is invalid.\n\n\nThis is also **invalid** Binary Tree, Why?\uD83E\uDD14\nThere are `2` roots which are `0` and `5`.\n\n\nFor sure, this is not a Binary Tree\uD83D\uDE20, Why?\nIt has a **cycle**\uD83D\uDEB4\u200D\u2640\uFE0F, 1 -> 4 -> 5 -> 1 -> 4 .....\n\n\nThis is a strange tree, or two trees ?\uD83E\uDD28\nThis graph has **multiple components** and **multiple roots**.\n\n**Multiple components** is when the graph has more than one piece like the last example.\n\n\nThis also strang \u2049\uD83E\uDD2F\nThis graph has **multiple components** but has only **one root**.\nwhich means that we must check for multiple **components** and multiple **root** **seperately**.\n\nI think we have a full picture \uD83D\uDDBC now about what will we do now.\n- Since we have **two arrays** indicating `left` and `right` children for each node then:\n - We will iterate over them to see if a node has **two parents**.\n - Search for the **root** that has no parents and if there are **multiple roots** then return `false`.\n - Check for **cycles**.\n - Check for **multiple components**.\n\nBut how to check for cycles and multiple components?\uD83E\uDD14\nWe want to traverse the graph to check that But any known traverse algorithms?\uD83E\uDD14\nYES, our today\'s heros\uD83E\uDDB8\u200D\u2642\uFE0F **BFS** and **DFS**.\n\nWe can use any algorithm of them and while using them we maintain `visited` array to mark nodes that were visited before and if we visited them again then we are sure there is a **cycle**.\uD83D\uDEB4\u200D\u2640\uFE0F\nBut how to check for multiple componenets.\uD83E\uDD28\nSimply, if we started **BFS** or **DFS** from the root and the given graph is a tree with only one connected component then for sure all nodes in visited array are **true** otherwise there will be some `true elements and false elements`.\nThese are the **full** steps to solve todays problem.\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n\n\n---\n\n\n\n# Proposed Approach\n## BFS or DFS\n1. Create an array called `childCount` of size `n` to **track** child which nodes **have** parents.\n2. **Update Child Count**:\n - Iterate through the `leftChild` array and For each left child:\n - If the left child exists (not -1), **mark** it as having a parent by setting `childCount[child]` to **true**.\n - Iterate through the `rightChild` array and For each right child:\n - If the right child exists (not -1), **mark** it as having a parent by setting `childCount[child]` to **true**.\n - If `childCount[child]` is **true**. Then there\'s `multiple parents for this child`.\n3. **Determine Root Node**:\n - Initialize a variable `root` to -1 (indicating no root found yet).\n - Iterate through the `childCount` array and For each node:\n - If the node has no parent (childCount[node] is **false**):\n - If `root` is -1 (no root assigned yet), set `root` to the current node.\n - If `root` is not -1 (`root already assigned`):\n - Return **false**, indicating multiple roots found.\n4. After that, If `root` is still -1 (`no root found`):\n - Return **false**, indicating no root found (`not a valid binary tree`).\n5. **Breadth-First Search for Valid Binary Tree (isBinaryTreeValid)**:\n - Initialize a `visited` array to **track** visited nodes and `queue` for BFS traversal.\n - Mark the **root** node as **visited** and **enqueue** it.\n - While the `queue` is not empty:\n - **Dequeue** a node and mark it as the current node.\n - Check the **left** child of the current node:\n - If it exists and is already **visited**, return **false** (`cycle detected`).\n - **Enqueue** the **left** child and mark it as **visited**.\n - Check the **right** child of the current node:\n - If it exists and is already **visited**, return **false** (`cycle detected`).\n - Enqueue the right child and mark it as visited.\n - **After** BFS, check if all nodes were visited:\n - If any node is **unvisited**, return **false**, indicating there\'s `multiple components`.\n - Return **true**, indicating a `valid binary tree`.\n5. **Depth-First Search for Valid Binary Tree (isBinaryTreeValid)**\n - It has the same steps like BFS but we will traverse through the tree recursively.\n\n\n## Complexity\n- **Time complexity:** $O(N)$\nSince we are Check for parents in `leftChild` array with cost `N` then Check for parents in `rightChild` array with cost `N` then search for `root` with cost `N` then doing `BFS` or `DFS` and we will traverse at most all nodes with cost `N` then we check for `multiple compenets` with cost `N`.\nThe total cost is `5 * N` which is `O(N)`.\n- **Space complexity:** $O(N)$\nSince we are storing if child has parent with cost `N` and `visited` array with cost `N` and the `queue` at most can have `N` nodes with cost `N`.\nThe total cost is `3 * N` which is `O(N)`.\n\n\n---\n\n\n\n# Code\n## 1. BFS\n``` C++ []\nclass Solution {\npublic:\n // Breadth-First Search to check if the given nodes form a valid binary tree\n bool isBinaryTreeValid(int root, vector<int>& leftChild, vector<int>& rightChild) {\n vector<bool> visited(leftChild.size(), false); // Tracks visited nodes\n queue<int> nodeQueue; // Queue for BFS traversal\n nodeQueue.push(root);\n visited[root] = true;\n\n while (!nodeQueue.empty()) {\n int current = nodeQueue.front();\n nodeQueue.pop();\n\n // Check left child\n if (leftChild[current] != -1) {\n if (visited[leftChild[current]]) // Check for cycle\n return false;\n\n nodeQueue.push(leftChild[current]);\n visited[leftChild[current]] = true; // Mark left child as visited\n }\n\n // Check right child\n if (rightChild[current] != -1) {\n if (visited[rightChild[current]]) // Check for cycle\n return false;\n\n nodeQueue.push(rightChild[current]);\n visited[rightChild[current]] = true; // Mark right child as visited\n }\n }\n\n // Check if there is multiple components\n for(int i = 0 ; i < visited.size() ; i ++)\n if(!visited[i])\n return false ;\n\n return true; // All nodes form a valid binary tree\n }\n\n bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {\n vector<bool> childCount(n, false); // Tracks child count for each node\n\n // Update child count based on leftChild\n for (auto child : leftChild) {\n // Check if node has child\n if (child != -1)\n childCount[child] = true; // Mark left child as having a parent\n }\n\n // Update child count based on rightChild\n for (auto child : rightChild) {\n // Check if node has child\n if (child != -1) {\n if (childCount[child]) // Check if the right child already has a parent\n return false;\n\n childCount[child] = true; // Mark right child as having a parent\n }\n }\n\n int root = -1; // Root node\n for (int i = 0; i < n; ++i) {\n if (!childCount[i]) {\n if (root == -1)\n root = i; // Set root node if not assigned\n else\n return false; // Multiple roots found, not a valid binary tree\n }\n }\n\n if (root == -1)\n return false; // No root found, not a valid binary tree\n\n return isBinaryTreeValid(root, leftChild, rightChild); // Check if the tree is valid\n }\n};\n```\n```Java []\nclass Solution {\n \n // Breadth-First Search to check if the given nodes form a valid binary tree\n private boolean isBinaryTreeValid(int root, int[] leftChild, int[] rightChild) {\n boolean[] visited = new boolean[leftChild.length]; // Tracks visited nodes\n Queue<Integer> nodeQueue = new LinkedList<>(); // Queue for BFS traversal\n nodeQueue.offer(root);\n visited[root] = true;\n\n while (!nodeQueue.isEmpty()) {\n int current = nodeQueue.poll();\n\n // Check left child\n if (leftChild[current] != -1) {\n if (visited[leftChild[current]]) // Check for cycle\n return false;\n\n nodeQueue.offer(leftChild[current]);\n visited[leftChild[current]] = true; // Mark left child as visited\n }\n\n // Check right child\n if (rightChild[current] != -1) {\n if (visited[rightChild[current]]) // Check for cycle\n return false;\n\n nodeQueue.offer(rightChild[current]);\n visited[rightChild[current]] = true; // Mark right child as visited\n }\n }\n\n // Check if there are multiple components\n for (boolean visit : visited) {\n if (!visit)\n return false;\n }\n\n return true; // All nodes form a valid binary tree\n }\n\n public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {\n boolean[] childCount = new boolean[n]; // Tracks child count for each node\n\n // Update child count based on leftChild\n for (int child : leftChild) {\n // Check if node has child\n if (child != -1)\n childCount[child] = true; // Mark left child as having a parent\n }\n\n // Update child count based on rightChild\n for (int child : rightChild) {\n // Check if node has child\n if (child != -1) {\n if (childCount[child]) // Check if the right child already has a parent\n return false;\n\n childCount[child] = true; // Mark right child as having a parent\n }\n }\n\n int root = -1; // Root node\n for (int i = 0; i < n; ++i) {\n if (!childCount[i]) {\n if (root == -1)\n root = i; // Set root node if not assigned\n else\n return false; // Multiple roots found, not a valid binary tree\n }\n }\n\n if (root == -1)\n return false; // No root found, not a valid binary tree\n\n return isBinaryTreeValid(root, leftChild, rightChild); // Check if the tree is valid\n }\n\n}\n```\n```Python []\nfrom queue import Queue\nclass Solution:\n def isBinaryTreeValid(self, root: int, leftChild: List[int], rightChild: List[int]) -> bool:\n visited = [False] * len(leftChild) # Tracks visited nodes\n nodeQueue = Queue() # Queue for BFS traversal\n nodeQueue.put(root)\n visited[root] = True\n\n while not nodeQueue.empty():\n current = nodeQueue.get()\n\n # Check left child\n if leftChild[current] != -1:\n if visited[leftChild[current]]: # Check for cycle\n return False\n\n nodeQueue.put(leftChild[current])\n visited[leftChild[current]] = True # Mark left child as visited\n\n # Check right child\n if rightChild[current] != -1:\n if visited[rightChild[current]]: # Check for cycle\n return False\n\n nodeQueue.put(rightChild[current])\n visited[rightChild[current]] = True # Mark right child as visited\n\n # Check if there are multiple components\n for visit in visited:\n if not visit:\n return False\n\n return True # All nodes form a valid binary tree\n\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n childCount = [False] * n # Tracks child count for each node\n\n # Update child count based on leftChild\n for child in leftChild:\n # Check if node has child\n if child != -1:\n childCount[child] = True # Mark left child as having a parent\n\n # Update child count based on rightChild\n for child in rightChild:\n # Check if node has child\n if child != -1:\n if childCount[child]: # Check if the right child already has a parent\n return False\n\n childCount[child] = True # Mark right child as having a parent\n\n root = -1 # Root node\n for i in range(n):\n if not childCount[i]:\n if root == -1:\n root = i # Set root node if not assigned\n else:\n return False # Multiple roots found, not a valid binary tree\n\n if root == -1:\n return False # No root found, not a valid binary tree\n\n return self.isBinaryTreeValid(root, leftChild, rightChild) # Check if the tree is valid\n\n```\n\n\n---\n\n\n## 2. DFS\n\n```C++ []\nclass Solution {\npublic:\n // Depth-First Search to check if the given nodes form a valid binary tree\n bool isBinaryTreeValid(int current, vector<int>& leftChild, vector<int>& rightChild, vector<bool>& visited) {\n // Check left child\n if (leftChild[current] != -1) {\n if (visited[leftChild[current]]) // Check for cycle\n return false;\n \n visited[leftChild[current]] = true; // Mark left child as visited\n if(!isBinaryTreeValid(leftChild[current], leftChild, rightChild, visited))\n return false;\n }\n \n // Check right child\n if (rightChild[current] != -1) {\n if (visited[rightChild[current]]) // Check for cycle\n return false;\n \n visited[rightChild[current]] = true; // Mark right child as visited\n if(!isBinaryTreeValid(rightChild[current], leftChild, rightChild, visited))\n return false ;\n }\n return true;\n }\n\n bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {\n vector<bool> childCount(n, false); // Tracks child count for each node\n\n // Update child count based on leftChild\n for (auto child : leftChild) {\n // Check if node has child\n if (child != -1)\n childCount[child] = true; // Mark left child as having a parent\n }\n\n // Update child count based on rightChild\n for (auto child : rightChild) {\n // Check if node has child\n if (child != -1) {\n if (childCount[child]) // Check if the right child already has a parent\n return false;\n\n childCount[child] = true; // Mark right child as having a parent\n }\n }\n\n int root = -1; // Root node\n for (int i = 0; i < n; ++i) {\n if (!childCount[i]) {\n if (root == -1)\n root = i; // Set root node if not assigned\n else\n return false; // Multiple roots found, not a valid binary tree\n }\n }\n\n if (root == -1)\n return false; // No root found, not a valid binary tree\n\n \n vector<bool> visited(n) ; // Tracks visited nodes\n visited[root] = true ;\n if(!isBinaryTreeValid(root, leftChild, rightChild, visited)) // Check if the tree is valid\n return false ;\n\n // Check if there is multiple components\n for(int i = 0 ; i < visited.size() ; i ++)\n if(!visited[i])\n return false ;\n\n return true; // All nodes form a valid binary tree\n }\n};\n```\n```Java []\nclass Solution {\n // Depth-First Search to check if the given nodes form a valid binary tree\n private boolean isBinaryTreeValid(int current, int[] leftChild, int[] rightChild, boolean[] visited) {\n // Check left child\n if (leftChild[current] != -1) {\n if (visited[leftChild[current]]) // Check for cycle\n return false;\n\n visited[leftChild[current]] = true; // Mark left child as visited\n if (!isBinaryTreeValid(leftChild[current], leftChild, rightChild, visited))\n return false;\n }\n\n // Check right child\n if (rightChild[current] != -1) {\n if (visited[rightChild[current]]) // Check for cycle\n return false;\n\n visited[rightChild[current]] = true; // Mark right child as visited\n if (!isBinaryTreeValid(rightChild[current], leftChild, rightChild, visited))\n return false;\n }\n return true;\n }\n\n public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {\n boolean[] childCount = new boolean[n]; // Tracks child count for each node\n\n // Update child count based on leftChild\n for (int child : leftChild) {\n // Check if node has child\n if (child != -1)\n childCount[child] = true; // Mark left child as having a parent\n }\n\n // Update child count based on rightChild\n for (int child : rightChild) {\n // Check if node has child\n if (child != -1) {\n if (childCount[child]) // Check if the right child already has a parent\n return false;\n\n childCount[child] = true; // Mark right child as having a parent\n }\n }\n\n int root = -1; // Root node\n for (int i = 0; i < n; ++i) {\n if (!childCount[i]) {\n if (root == -1)\n root = i; // Set root node if not assigned\n else\n return false; // Multiple roots found, not a valid binary tree\n }\n }\n\n if (root == -1)\n return false; // No root found, not a valid binary tree\n\n boolean[] visited = new boolean[n]; // Tracks visited nodes\n visited[root] = true;\n if (!isBinaryTreeValid(root, leftChild, rightChild, visited)) // Check if the tree is valid\n return false;\n\n // Check if there is multiple components\n for (boolean visit : visited)\n if (!visit)\n return false;\n\n return true; // All nodes form a valid binary tree\n }\n}\n```\n```Python []\nclass Solution:\n def isBinaryTreeValid(self, current, leftChild, rightChild, visited):\n # Check left child\n if leftChild[current] != -1:\n if visited[leftChild[current]]: # Check for cycle\n return False\n\n visited[leftChild[current]] = True # Mark left child as visited\n if not self.isBinaryTreeValid(leftChild[current], leftChild, rightChild, visited):\n return False\n\n # Check right child\n if rightChild[current] != -1:\n if visited[rightChild[current]]: # Check for cycle\n return False\n\n visited[rightChild[current]] = True # Mark right child as visited\n if not self.isBinaryTreeValid(rightChild[current], leftChild, rightChild, visited):\n return False\n\n return True\n\n def validateBinaryTreeNodes(self, n, leftChild, rightChild):\n childCount = [False] * n # Tracks child count for each node\n\n # Update child count based on leftChild\n for child in leftChild:\n # Check if node has child\n if child != -1:\n childCount[child] = True # Mark left child as having a parent\n\n # Update child count based on rightChild\n for child in rightChild:\n # Check if node has child\n if child != -1:\n if childCount[child]: # Check if the right child already has a parent\n return False\n\n childCount[child] = True # Mark right child as having a parent\n\n root = -1 # Root node\n for i in range(n):\n if not childCount[i]:\n if root == -1:\n root = i # Set root node if not assigned\n else:\n return False # Multiple roots found, not a valid binary tree\n\n if root == -1:\n return False # No root found, not a valid binary tree\n\n visited = [False] * n # Tracks visited nodes\n visited[root] = True\n if not self.isBinaryTreeValid(root, leftChild, rightChild, visited): # Check if the tree is valid\n return False\n\n # Check if there is multiple components\n for visit in visited:\n if not visit:\n return False\n\n return True # All nodes form a valid binary tree\n```\n\n\n\n\n\n\n | 93 | You have `n` binary tree nodes numbered from `0` to `n - 1` where node `i` has two children `leftChild[i]` and `rightChild[i]`, return `true` if and only if **all** the given nodes form **exactly one** valid binary tree.
If node `i` has no left child then `leftChild[i]` will equal `-1`, similarly for the right child.
Note that the nodes have no values and that we only use the node numbers in this problem.
**Example 1:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,-1,-1,-1\]
**Output:** true
**Example 2:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,3,-1,-1\]
**Output:** false
**Example 3:**
**Input:** n = 2, leftChild = \[1,0\], rightChild = \[-1,-1\]
**Output:** false
**Constraints:**
* `n == leftChild.length == rightChild.length`
* `1 <= n <= 104`
* `-1 <= leftChild[i], rightChild[i] <= n - 1` | Can you use backtracking to solve this problem ?. Suppose you've placed a bunch of squares. Where is the natural spot to place the next square ?. The maximum number of squares to be placed will be ≤ max(n,m). |
🚀 93.31% || BFS & DFS || Explained Intuition🚀 | validate-binary-tree-nodes | 1 | 1 | # Porblem Description\n\nGiven `n` binary tree nodes numbered from `0` to `n - 1`, represented by arrays `leftChild` and `rightChild` where each element corresponds to the `left` and `right` child of a node respectively, **determine** if the provided nodes **form** exactly one **valid** binary tree. \nA node with **no left** child is represented by `-1` in the `leftChild` array, and **similarly** for a node with **no right** child in the `rightChild` array. \nThe **goal** is to verify if the given nodes, identified solely by their numbers, constitute a **valid** binary tree structure.\n\n- **Constraints:**\n - `n == leftChild.length == rightChild.length`\n - `1 <= n <= 10e4`\n - `-1 <= leftChild[i], rightChild[i] <= n - 1`\n\n\n---\n\n# Intuition\n\nHi there, \uD83D\uDE03\n\nLet\'s deep dive\uD83E\uDD3F in our today\'s Interesting problem.\nThe goal in our ptoblem is to **validate** if a given nodes can form a **valid Binary Tree Structure**\uD83C\uDF32.\n\nBut what is the structure of a binary tree\u2753\n- Simply:\n - Each node has only **one parent** (Except for the root).\n - There is only **one root**.\n - Each node has at most **2 children** (leaf nodes have no children).\n - There is **no Cycle**.\uD83D\uDEB4\u200D\u2640\uFE0F\n\nSeems Valid \u2714\nLet\'s take a look at these trees\uD83C\uDF32\uD83C\uDF33.\n\nThis is **invalid** Binary Tree, Why?\uD83E\uDD14\nnode `4` have `2` parents which is invalid.\n\n\nThis is also **invalid** Binary Tree, Why?\uD83E\uDD14\nThere are `2` roots which are `0` and `5`.\n\n\nFor sure, this is not a Binary Tree\uD83D\uDE20, Why?\nIt has a **cycle**\uD83D\uDEB4\u200D\u2640\uFE0F, 1 -> 4 -> 5 -> 1 -> 4 .....\n\n\nThis is a strange tree, or two trees ?\uD83E\uDD28\nThis graph has **multiple components** and **multiple roots**.\n\n**Multiple components** is when the graph has more than one piece like the last example.\n\n\nThis also strang \u2049\uD83E\uDD2F\nThis graph has **multiple components** but has only **one root**.\nwhich means that we must check for multiple **components** and multiple **root** **seperately**.\n\nI think we have a full picture \uD83D\uDDBC now about what will we do now.\n- Since we have **two arrays** indicating `left` and `right` children for each node then:\n - We will iterate over them to see if a node has **two parents**.\n - Search for the **root** that has no parents and if there are **multiple roots** then return `false`.\n - Check for **cycles**.\n - Check for **multiple components**.\n\nBut how to check for cycles and multiple components?\uD83E\uDD14\nWe want to traverse the graph to check that But any known traverse algorithms?\uD83E\uDD14\nYES, our today\'s heros\uD83E\uDDB8\u200D\u2642\uFE0F **BFS** and **DFS**.\n\nWe can use any algorithm of them and while using them we maintain `visited` array to mark nodes that were visited before and if we visited them again then we are sure there is a **cycle**.\uD83D\uDEB4\u200D\u2640\uFE0F\nBut how to check for multiple componenets.\uD83E\uDD28\nSimply, if we started **BFS** or **DFS** from the root and the given graph is a tree with only one connected component then for sure all nodes in visited array are **true** otherwise there will be some `true elements and false elements`.\nThese are the **full** steps to solve todays problem.\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n\n\n---\n\n\n\n# Proposed Approach\n## BFS or DFS\n1. Create an array called `childCount` of size `n` to **track** child which nodes **have** parents.\n2. **Update Child Count**:\n - Iterate through the `leftChild` array and For each left child:\n - If the left child exists (not -1), **mark** it as having a parent by setting `childCount[child]` to **true**.\n - Iterate through the `rightChild` array and For each right child:\n - If the right child exists (not -1), **mark** it as having a parent by setting `childCount[child]` to **true**.\n - If `childCount[child]` is **true**. Then there\'s `multiple parents for this child`.\n3. **Determine Root Node**:\n - Initialize a variable `root` to -1 (indicating no root found yet).\n - Iterate through the `childCount` array and For each node:\n - If the node has no parent (childCount[node] is **false**):\n - If `root` is -1 (no root assigned yet), set `root` to the current node.\n - If `root` is not -1 (`root already assigned`):\n - Return **false**, indicating multiple roots found.\n4. After that, If `root` is still -1 (`no root found`):\n - Return **false**, indicating no root found (`not a valid binary tree`).\n5. **Breadth-First Search for Valid Binary Tree (isBinaryTreeValid)**:\n - Initialize a `visited` array to **track** visited nodes and `queue` for BFS traversal.\n - Mark the **root** node as **visited** and **enqueue** it.\n - While the `queue` is not empty:\n - **Dequeue** a node and mark it as the current node.\n - Check the **left** child of the current node:\n - If it exists and is already **visited**, return **false** (`cycle detected`).\n - **Enqueue** the **left** child and mark it as **visited**.\n - Check the **right** child of the current node:\n - If it exists and is already **visited**, return **false** (`cycle detected`).\n - Enqueue the right child and mark it as visited.\n - **After** BFS, check if all nodes were visited:\n - If any node is **unvisited**, return **false**, indicating there\'s `multiple components`.\n - Return **true**, indicating a `valid binary tree`.\n5. **Depth-First Search for Valid Binary Tree (isBinaryTreeValid)**\n - It has the same steps like BFS but we will traverse through the tree recursively.\n\n\n## Complexity\n- **Time complexity:** $O(N)$\nSince we are Check for parents in `leftChild` array with cost `N` then Check for parents in `rightChild` array with cost `N` then search for `root` with cost `N` then doing `BFS` or `DFS` and we will traverse at most all nodes with cost `N` then we check for `multiple compenets` with cost `N`.\nThe total cost is `5 * N` which is `O(N)`.\n- **Space complexity:** $O(N)$\nSince we are storing if child has parent with cost `N` and `visited` array with cost `N` and the `queue` at most can have `N` nodes with cost `N`.\nThe total cost is `3 * N` which is `O(N)`.\n\n\n---\n\n\n\n# Code\n## 1. BFS\n``` C++ []\nclass Solution {\npublic:\n // Breadth-First Search to check if the given nodes form a valid binary tree\n bool isBinaryTreeValid(int root, vector<int>& leftChild, vector<int>& rightChild) {\n vector<bool> visited(leftChild.size(), false); // Tracks visited nodes\n queue<int> nodeQueue; // Queue for BFS traversal\n nodeQueue.push(root);\n visited[root] = true;\n\n while (!nodeQueue.empty()) {\n int current = nodeQueue.front();\n nodeQueue.pop();\n\n // Check left child\n if (leftChild[current] != -1) {\n if (visited[leftChild[current]]) // Check for cycle\n return false;\n\n nodeQueue.push(leftChild[current]);\n visited[leftChild[current]] = true; // Mark left child as visited\n }\n\n // Check right child\n if (rightChild[current] != -1) {\n if (visited[rightChild[current]]) // Check for cycle\n return false;\n\n nodeQueue.push(rightChild[current]);\n visited[rightChild[current]] = true; // Mark right child as visited\n }\n }\n\n // Check if there is multiple components\n for(int i = 0 ; i < visited.size() ; i ++)\n if(!visited[i])\n return false ;\n\n return true; // All nodes form a valid binary tree\n }\n\n bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {\n vector<bool> childCount(n, false); // Tracks child count for each node\n\n // Update child count based on leftChild\n for (auto child : leftChild) {\n // Check if node has child\n if (child != -1)\n childCount[child] = true; // Mark left child as having a parent\n }\n\n // Update child count based on rightChild\n for (auto child : rightChild) {\n // Check if node has child\n if (child != -1) {\n if (childCount[child]) // Check if the right child already has a parent\n return false;\n\n childCount[child] = true; // Mark right child as having a parent\n }\n }\n\n int root = -1; // Root node\n for (int i = 0; i < n; ++i) {\n if (!childCount[i]) {\n if (root == -1)\n root = i; // Set root node if not assigned\n else\n return false; // Multiple roots found, not a valid binary tree\n }\n }\n\n if (root == -1)\n return false; // No root found, not a valid binary tree\n\n return isBinaryTreeValid(root, leftChild, rightChild); // Check if the tree is valid\n }\n};\n```\n```Java []\nclass Solution {\n \n // Breadth-First Search to check if the given nodes form a valid binary tree\n private boolean isBinaryTreeValid(int root, int[] leftChild, int[] rightChild) {\n boolean[] visited = new boolean[leftChild.length]; // Tracks visited nodes\n Queue<Integer> nodeQueue = new LinkedList<>(); // Queue for BFS traversal\n nodeQueue.offer(root);\n visited[root] = true;\n\n while (!nodeQueue.isEmpty()) {\n int current = nodeQueue.poll();\n\n // Check left child\n if (leftChild[current] != -1) {\n if (visited[leftChild[current]]) // Check for cycle\n return false;\n\n nodeQueue.offer(leftChild[current]);\n visited[leftChild[current]] = true; // Mark left child as visited\n }\n\n // Check right child\n if (rightChild[current] != -1) {\n if (visited[rightChild[current]]) // Check for cycle\n return false;\n\n nodeQueue.offer(rightChild[current]);\n visited[rightChild[current]] = true; // Mark right child as visited\n }\n }\n\n // Check if there are multiple components\n for (boolean visit : visited) {\n if (!visit)\n return false;\n }\n\n return true; // All nodes form a valid binary tree\n }\n\n public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {\n boolean[] childCount = new boolean[n]; // Tracks child count for each node\n\n // Update child count based on leftChild\n for (int child : leftChild) {\n // Check if node has child\n if (child != -1)\n childCount[child] = true; // Mark left child as having a parent\n }\n\n // Update child count based on rightChild\n for (int child : rightChild) {\n // Check if node has child\n if (child != -1) {\n if (childCount[child]) // Check if the right child already has a parent\n return false;\n\n childCount[child] = true; // Mark right child as having a parent\n }\n }\n\n int root = -1; // Root node\n for (int i = 0; i < n; ++i) {\n if (!childCount[i]) {\n if (root == -1)\n root = i; // Set root node if not assigned\n else\n return false; // Multiple roots found, not a valid binary tree\n }\n }\n\n if (root == -1)\n return false; // No root found, not a valid binary tree\n\n return isBinaryTreeValid(root, leftChild, rightChild); // Check if the tree is valid\n }\n\n}\n```\n```Python []\nfrom queue import Queue\nclass Solution:\n def isBinaryTreeValid(self, root: int, leftChild: List[int], rightChild: List[int]) -> bool:\n visited = [False] * len(leftChild) # Tracks visited nodes\n nodeQueue = Queue() # Queue for BFS traversal\n nodeQueue.put(root)\n visited[root] = True\n\n while not nodeQueue.empty():\n current = nodeQueue.get()\n\n # Check left child\n if leftChild[current] != -1:\n if visited[leftChild[current]]: # Check for cycle\n return False\n\n nodeQueue.put(leftChild[current])\n visited[leftChild[current]] = True # Mark left child as visited\n\n # Check right child\n if rightChild[current] != -1:\n if visited[rightChild[current]]: # Check for cycle\n return False\n\n nodeQueue.put(rightChild[current])\n visited[rightChild[current]] = True # Mark right child as visited\n\n # Check if there are multiple components\n for visit in visited:\n if not visit:\n return False\n\n return True # All nodes form a valid binary tree\n\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n childCount = [False] * n # Tracks child count for each node\n\n # Update child count based on leftChild\n for child in leftChild:\n # Check if node has child\n if child != -1:\n childCount[child] = True # Mark left child as having a parent\n\n # Update child count based on rightChild\n for child in rightChild:\n # Check if node has child\n if child != -1:\n if childCount[child]: # Check if the right child already has a parent\n return False\n\n childCount[child] = True # Mark right child as having a parent\n\n root = -1 # Root node\n for i in range(n):\n if not childCount[i]:\n if root == -1:\n root = i # Set root node if not assigned\n else:\n return False # Multiple roots found, not a valid binary tree\n\n if root == -1:\n return False # No root found, not a valid binary tree\n\n return self.isBinaryTreeValid(root, leftChild, rightChild) # Check if the tree is valid\n\n```\n\n\n---\n\n\n## 2. DFS\n\n```C++ []\nclass Solution {\npublic:\n // Depth-First Search to check if the given nodes form a valid binary tree\n bool isBinaryTreeValid(int current, vector<int>& leftChild, vector<int>& rightChild, vector<bool>& visited) {\n // Check left child\n if (leftChild[current] != -1) {\n if (visited[leftChild[current]]) // Check for cycle\n return false;\n \n visited[leftChild[current]] = true; // Mark left child as visited\n if(!isBinaryTreeValid(leftChild[current], leftChild, rightChild, visited))\n return false;\n }\n \n // Check right child\n if (rightChild[current] != -1) {\n if (visited[rightChild[current]]) // Check for cycle\n return false;\n \n visited[rightChild[current]] = true; // Mark right child as visited\n if(!isBinaryTreeValid(rightChild[current], leftChild, rightChild, visited))\n return false ;\n }\n return true;\n }\n\n bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {\n vector<bool> childCount(n, false); // Tracks child count for each node\n\n // Update child count based on leftChild\n for (auto child : leftChild) {\n // Check if node has child\n if (child != -1)\n childCount[child] = true; // Mark left child as having a parent\n }\n\n // Update child count based on rightChild\n for (auto child : rightChild) {\n // Check if node has child\n if (child != -1) {\n if (childCount[child]) // Check if the right child already has a parent\n return false;\n\n childCount[child] = true; // Mark right child as having a parent\n }\n }\n\n int root = -1; // Root node\n for (int i = 0; i < n; ++i) {\n if (!childCount[i]) {\n if (root == -1)\n root = i; // Set root node if not assigned\n else\n return false; // Multiple roots found, not a valid binary tree\n }\n }\n\n if (root == -1)\n return false; // No root found, not a valid binary tree\n\n \n vector<bool> visited(n) ; // Tracks visited nodes\n visited[root] = true ;\n if(!isBinaryTreeValid(root, leftChild, rightChild, visited)) // Check if the tree is valid\n return false ;\n\n // Check if there is multiple components\n for(int i = 0 ; i < visited.size() ; i ++)\n if(!visited[i])\n return false ;\n\n return true; // All nodes form a valid binary tree\n }\n};\n```\n```Java []\nclass Solution {\n // Depth-First Search to check if the given nodes form a valid binary tree\n private boolean isBinaryTreeValid(int current, int[] leftChild, int[] rightChild, boolean[] visited) {\n // Check left child\n if (leftChild[current] != -1) {\n if (visited[leftChild[current]]) // Check for cycle\n return false;\n\n visited[leftChild[current]] = true; // Mark left child as visited\n if (!isBinaryTreeValid(leftChild[current], leftChild, rightChild, visited))\n return false;\n }\n\n // Check right child\n if (rightChild[current] != -1) {\n if (visited[rightChild[current]]) // Check for cycle\n return false;\n\n visited[rightChild[current]] = true; // Mark right child as visited\n if (!isBinaryTreeValid(rightChild[current], leftChild, rightChild, visited))\n return false;\n }\n return true;\n }\n\n public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {\n boolean[] childCount = new boolean[n]; // Tracks child count for each node\n\n // Update child count based on leftChild\n for (int child : leftChild) {\n // Check if node has child\n if (child != -1)\n childCount[child] = true; // Mark left child as having a parent\n }\n\n // Update child count based on rightChild\n for (int child : rightChild) {\n // Check if node has child\n if (child != -1) {\n if (childCount[child]) // Check if the right child already has a parent\n return false;\n\n childCount[child] = true; // Mark right child as having a parent\n }\n }\n\n int root = -1; // Root node\n for (int i = 0; i < n; ++i) {\n if (!childCount[i]) {\n if (root == -1)\n root = i; // Set root node if not assigned\n else\n return false; // Multiple roots found, not a valid binary tree\n }\n }\n\n if (root == -1)\n return false; // No root found, not a valid binary tree\n\n boolean[] visited = new boolean[n]; // Tracks visited nodes\n visited[root] = true;\n if (!isBinaryTreeValid(root, leftChild, rightChild, visited)) // Check if the tree is valid\n return false;\n\n // Check if there is multiple components\n for (boolean visit : visited)\n if (!visit)\n return false;\n\n return true; // All nodes form a valid binary tree\n }\n}\n```\n```Python []\nclass Solution:\n def isBinaryTreeValid(self, current, leftChild, rightChild, visited):\n # Check left child\n if leftChild[current] != -1:\n if visited[leftChild[current]]: # Check for cycle\n return False\n\n visited[leftChild[current]] = True # Mark left child as visited\n if not self.isBinaryTreeValid(leftChild[current], leftChild, rightChild, visited):\n return False\n\n # Check right child\n if rightChild[current] != -1:\n if visited[rightChild[current]]: # Check for cycle\n return False\n\n visited[rightChild[current]] = True # Mark right child as visited\n if not self.isBinaryTreeValid(rightChild[current], leftChild, rightChild, visited):\n return False\n\n return True\n\n def validateBinaryTreeNodes(self, n, leftChild, rightChild):\n childCount = [False] * n # Tracks child count for each node\n\n # Update child count based on leftChild\n for child in leftChild:\n # Check if node has child\n if child != -1:\n childCount[child] = True # Mark left child as having a parent\n\n # Update child count based on rightChild\n for child in rightChild:\n # Check if node has child\n if child != -1:\n if childCount[child]: # Check if the right child already has a parent\n return False\n\n childCount[child] = True # Mark right child as having a parent\n\n root = -1 # Root node\n for i in range(n):\n if not childCount[i]:\n if root == -1:\n root = i # Set root node if not assigned\n else:\n return False # Multiple roots found, not a valid binary tree\n\n if root == -1:\n return False # No root found, not a valid binary tree\n\n visited = [False] * n # Tracks visited nodes\n visited[root] = True\n if not self.isBinaryTreeValid(root, leftChild, rightChild, visited): # Check if the tree is valid\n return False\n\n # Check if there is multiple components\n for visit in visited:\n if not visit:\n return False\n\n return True # All nodes form a valid binary tree\n```\n\n\n\n\n\n\n | 93 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
✅☑[C++/C/Java/Python/JavaScript] || 3 Approaches || Optimized || EXPLAINED🔥 | validate-binary-tree-nodes | 0 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### *Approach 1 (DFS)*\n1. `validateBinaryTreeNodes` is the main function that takes three parameters:\n\n - `n`: The total number of nodes in the tree.\n - `leftChild`: A vector representing the left child of each node. A value of -1 means there is no left child.\n - `rightChild`: A vector representing the right child of each node. A value of -1 means there is no right child.\n1. It first calls the `findRoot` function to determine the root node of the tree. The `findRoot` function:\n\n - Initializes a set called `children` to store the children of all nodes.\n - Adds the indices of left and right children to the `children` set.\n - Iterates through indices from 0 to `n-1` to find the node that is not present in the `children` set. This node is considered the root.\n - If there\'s no unique root, the function returns -1.\n1. If there is no unique root (i.e., `root` is -1), the function returns `false` because a valid tree must have exactly one root.\n\n1. It then uses depth-first search (DFS) to traverse the tree starting from the root node:\n\n - Initializes a set `seen` to keep track of visited nodes.\n - Initializes a `stack` stack for DFS.\n - Inserts the root into the `seen` set and pushes it onto the stack.\n1. In the DFS loop:\n\n - Pops the top node from the stack.\n - Checks its left and right children (if they exist) and whether they have already been seen. If a child has been seen, this means there\'s a cycle in the tree, so the function returns `false`.\n - If a child has not been seen, it is pushed onto the stack and added to the `seen` set.\n1. After the DFS traversal, the function checks if the number of nodes in the `seen` set is equal to `n`. If it is, this means all nodes in the tree were visited without any cycles, so the tree is valid, and the function returns `true`.\n\n1. If there were any cycles or some nodes were not reachable from the root, the function returns `false`.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {\n int root = findRoot(n, leftChild, rightChild);\n if (root == -1) {\n return false;\n }\n \n unordered_set<int> seen;\n stack<int> stack;\n seen.insert(root);\n stack.push(root);\n \n while (!stack.empty()) {\n int node = stack.top();\n stack.pop();\n \n int children[] = {leftChild[node], rightChild[node]};\n for (int child : children) {\n if (child != -1) {\n if (seen.find(child) != seen.end()) {\n return false;\n }\n \n stack.push(child);\n seen.insert(child);\n }\n }\n }\n \n return seen.size() == n;\n }\n \n int findRoot(int n, vector<int>& left, vector<int>& right) {\n unordered_set<int> children;\n children.insert(left.begin(), left.end());\n children.insert(right.begin(), right.end());\n \n for (int i = 0; i < n; i++) {\n if (children.find(i) == children.end()) {\n return i;\n }\n }\n \n return -1;\n }\n};\n```\n\n\n```C []\n\nint findRoot(int n, int* left, int* right) {\n int* children = (int*)malloc(n * sizeof(int));\n if (!children) {\n return -1;\n }\n \n for (int i = 0; i < n; i++) {\n children[i] = 0;\n }\n\n for (int i = 0; i < n; i++) {\n if (left[i] != -1) {\n children[left[i]] = 1;\n }\n if (right[i] != -1) {\n children[right[i]] = 1;\n }\n }\n\n for (int i = 0; i < n; i++) {\n if (children[i] == 0) {\n free(children);\n return i;\n }\n }\n\n free(children);\n return -1;\n}\n\n// Function to validate the binary tree nodes\nbool validateBinaryTreeNodes(int n, int* leftChild, int* rightChild) {\n int root = findRoot(n, leftChild, rightChild);\n if (root == -1) {\n return false;\n }\n\n int* seen = (int*)malloc(n * sizeof(int));\n if (!seen) {\n return false;\n }\n \n for (int i = 0; i < n; i++) {\n seen[i] = 0;\n }\n\n int* stack = (int*)malloc(n * sizeof(int));\n if (!stack) {\n free(seen);\n return false;\n }\n\n int stackTop = -1;\n seen[root] = 1;\n stack[++stackTop] = root;\n\n while (stackTop >= 0) {\n int node = stack[stackTop--];\n int children[] = {leftChild[node], rightChild[node]};\n\n for (int i = 0; i < 2; i++) {\n int child = children[i];\n if (child != -1) {\n if (seen[child] == 1) {\n free(stack);\n free(seen);\n return false;\n }\n\n stack[++stackTop] = child;\n seen[child] = 1;\n }\n }\n }\n\n free(stack);\n free(seen);\n\n return true;\n}\n\n```\n\n```Java []\nclass Solution {\n public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {\n int root = findRoot(n, leftChild, rightChild);\n if (root == -1) {\n return false;\n }\n \n Set<Integer> seen = new HashSet<>();\n Stack<Integer> stack = new Stack<>();\n seen.add(root);\n stack.push(root);\n \n while (!stack.isEmpty()) {\n int node = stack.pop();\n int[] children = {leftChild[node], rightChild[node]};\n \n for (int child : children) {\n if (child != -1) {\n if (seen.contains(child)) {\n return false;\n }\n \n stack.push(child);\n seen.add(child);\n }\n }\n \n }\n \n return seen.size() == n;\n }\n \n public int findRoot(int n, int[] left, int[] right) {\n Set<Integer> children = new HashSet<>();\n for (int node : left) {\n children.add(node);\n }\n \n for (int node : right) {\n children.add(node);\n }\n \n for (int i = 0; i < n; i++) {\n if (!children.contains(i)) {\n return i;\n }\n }\n \n return -1;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n def find_root():\n children = set(leftChild) | set(rightChild)\n \n for i in range(n):\n if i not in children:\n return i\n \n return -1\n \n root = find_root()\n if root == -1:\n return False\n \n seen = {root}\n stack = [root]\n while stack:\n node = stack.pop()\n for child in [leftChild[node], rightChild[node]]:\n if child != -1:\n if child in seen:\n return False\n \n stack.append(child)\n seen.add(child)\n \n return len(seen) == n\n\n```\n\n```javascript []\nfunction findRoot(n, left, right) {\n const children = new Set();\n\n for (let i = 0; i < n; i++) {\n if (left[i] !== -1) {\n children.add(left[i]);\n }\n if (right[i] !== -1) {\n children.add(right[i]);\n }\n }\n\n for (let i = 0; i < n; i++) {\n if (!children.has(i)) {\n return i;\n }\n }\n\n return -1;\n}\n\n/**\n * Function to validate the binary tree nodes\n * @param {number} n\n * @param {number[]} leftChild\n * @param {number[]} rightChild\n * @returns {boolean}\n */\nfunction validateBinaryTreeNodes(n, leftChild, rightChild) {\n const root = findRoot(n, leftChild, rightChild);\n if (root === -1) {\n return false;\n }\n\n const seen = new Array(n).fill(0);\n const stack = [];\n seen[root] = 1;\n stack.push(root);\n\n while (stack.length > 0) {\n const node = stack.pop();\n const children = [leftChild[node], rightChild[node]];\n\n for (const child of children) {\n if (child !== -1) {\n if (seen[child] === 1) {\n return false;\n }\n stack.push(child);\n seen[child] = 1;\n }\n }\n }\n\n return true;\n}\n```\n\n\n---\n\n#### *Approach 2 (BFS)*\n1. `validateBinaryTreeNodes` function:\n\n - This function takes three arguments: `n` (the number of nodes), `leftChild` (a vector representing the left child of each node), and `rightChild` (a vector representing the right child of each node).\n - It first calls the `findRoot` function to find the root node of the binary tree.\n - If the root is not found (i.e., `findRoot` returns -1), it returns `false` because a valid binary tree must have a single root node.\n - It uses an unordered set `seen` to keep track of nodes that have been visited and a queue `queue` for breadth-first traversal.\n - The root node is marked as seen and added to the queue.\n - It enters a loop to process nodes while the queue is not empty.\n - Inside the loop, it dequeues a node from the front of the queue and checks its children.\n - It uses an array `children` to represent the left and right children of the current node.\n - For each child, if it exists (i.e., not -1) and is already seen, it returns `false` because a valid binary tree should not have any duplicate nodes.\n - If the child is valid and not seen, it enqueues the child, marks it as seen, and continues.\n - The loop continues until all nodes are processed.\n - After the loop, it checks if the number of seen nodes is equal to `n`, which indicates that all nodes were visited. If true, it returns `true`, indicating a valid binary tree.\n2. `findRoot` function:\n\n - This function is responsible for finding the root of the binary tree. It takes the same arguments as `validateBinaryTreeNodes`.\n - It uses an unordered set `children` to keep track of nodes that are children of some other node.\n - It iterates through the nodes from 0 to `n-1` and adds their values to the `children` set if they are present as children in `leftChild` or `rightChild`.\n - The first node that is not in the `children` set is considered the root, and its index is returned.\n - If no such node is found (all nodes are children), it returns -1, indicating the absence of a root.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {\n int root = findRoot(n, leftChild, rightChild);\n if (root == -1) {\n return false;\n }\n \n unordered_set<int> seen;\n queue<int> queue;\n seen.insert(root);\n queue.push(root);\n \n while (!queue.empty()) {\n int node = queue.front();\n queue.pop();\n \n int children[] = {leftChild[node], rightChild[node]};\n for (int child : children) {\n if (child != -1) {\n if (seen.find(child) != seen.end()) {\n return false;\n }\n \n queue.push(child);\n seen.insert(child);\n }\n }\n }\n \n return seen.size() == n;\n }\n \n int findRoot(int n, vector<int>& left, vector<int>& right) {\n unordered_set<int> children;\n children.insert(left.begin(), left.end());\n children.insert(right.begin(), right.end());\n \n for (int i = 0; i < n; i++) {\n if (children.find(i) == children.end()) {\n return i;\n }\n }\n \n return -1;\n }\n};\n```\n\n\n```C []\nbool validateBinaryTreeNodes(int n, int* leftChild, int* rightChild) {\n int root = findRoot(n, leftChild, rightChild);\n if (root == -1) {\n return false;\n }\n\n int* seen = (int*)calloc(n, sizeof(int));\n int* queue = (int*)calloc(n, sizeof(int));\n int front = 0, rear = 0;\n\n seen[root] = 1;\n queue[rear++] = root;\n\n while (front < rear) {\n int node = queue[front++];\n \n int children[2] = {leftChild[node], rightChild[node]};\n for (int i = 0; i < 2; i++) {\n int child = children[i];\n if (child != -1) {\n if (seen[child]) {\n free(seen);\n free(queue);\n return false;\n }\n\n queue[rear++] = child;\n seen[child] = 1;\n }\n }\n }\n\n free(seen);\n free(queue);\n\n return front == n;\n}\n\nint findRoot(int n, int* left, int* right) {\n int* children = (int*)calloc(n, sizeof(int));\n\n for (int i = 0; i < n; i++) {\n children[left[i]] = 1;\n children[right[i]] = 1;\n }\n\n for (int i = 0; i < n; i++) {\n if (!children[i]) {\n free(children);\n return i;\n }\n }\n\n free(children);\n return -1;\n}\n\n\n```\n\n```Java []\nclass Solution {\n public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {\n int root = findRoot(n, leftChild, rightChild);\n if (root == -1) {\n return false;\n }\n \n Set<Integer> seen = new HashSet<>();\n Queue<Integer> queue = new LinkedList<>();\n seen.add(root);\n queue.add(root);\n \n while (!queue.isEmpty()) {\n int node = queue.remove();\n int[] children = {leftChild[node], rightChild[node]};\n \n for (int child : children) {\n if (child != -1) {\n if (seen.contains(child)) {\n return false;\n }\n \n queue.add(child);\n seen.add(child);\n }\n }\n \n }\n \n return seen.size() == n;\n }\n \n public int findRoot(int n, int[] left, int[] right) {\n Set<Integer> children = new HashSet<>();\n for (int node : left) {\n children.add(node);\n }\n \n for (int node : right) {\n children.add(node);\n }\n \n for (int i = 0; i < n; i++) {\n if (!children.contains(i)) {\n return i;\n }\n }\n \n return -1;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n def find_root():\n children = set(leftChild) | set(rightChild)\n \n for i in range(n):\n if i not in children:\n return i\n \n return -1\n \n root = find_root()\n if root == -1:\n return False\n \n seen = {root}\n queue = deque([root])\n while queue:\n node = queue.popleft()\n for child in [leftChild[node], rightChild[node]]:\n if child != -1:\n if child in seen:\n return False\n \n queue.append(child)\n seen.add(child)\n \n return len(seen) == n\n\n```\n\n```javascript []\nfunction validateBinaryTreeNodes(n, leftChild, rightChild) {\n const root = findRoot(n, leftChild, rightChild);\n if (root === -1) {\n return false;\n }\n\n const seen = new Set();\n const queue = [];\n seen.add(root);\n queue.push(root);\n\n while (queue.length > 0) {\n const node = queue.shift();\n\n const children = [leftChild[node], rightChild[node]];\n for (const child of children) {\n if (child !== -1) {\n if (seen.has(child)) {\n return false;\n }\n\n queue.push(child);\n seen.add(child);\n }\n }\n }\n\n return seen.size === n;\n}\n\nfunction findRoot(n, left, right) {\n const children = new Set();\n for (let i = 0; i < n; i++) {\n children.add(left[i]);\n children.add(right[i]);\n }\n\n for (let i = 0; i < n; i++) {\n if (!children.has(i)) {\n return i;\n }\n }\n\n return -1;\n}\n\n```\n\n\n---\n#### *Approach 3 (Union Find)*\n1. **Union-Find (Disjoint Set) Data Structure:**\n\n - A Union-Find data structure is used for efficiently handling sets of elements and checking for connectivity among them.\n1. **UnionFind Class:**\n\n - The `UnionFind` class is defined to represent a disjoint-set data structure.\n - It keeps track of the number of components (connected sets) and the parents (representatives) of individual elements.\n - The `UnionFind` constructor initializes the data structure with \'n\' elements, where each element is its own parent, and there are initially \'n\' components.\n1. **join Method:**\n\n - The `join` method is used to combine two elements (nodes) if they are not already part of the same component. It checks whether the parent of the child is the same as the child (indicating it\'s the representative) and whether the parent of the parent is the same as the child (indicating they are already part of the same component).\n - If they meet these criteria, it means they are part of the same component and should not be joined, so it returns `false`. Otherwise, it performs the union operation by making the parent of the child\'s parent the same as the parent, effectively joining the two components. It also decrements the component count.\n1. **find Method:**\n\n - The `find` method returns the representative (parent) of a given element. It utilizes path compression, which means that while finding the parent, it also updates the parent of the current element to the representative. This helps in optimizing future find operations.\n1. **Solution Class:**\n\n - The `Solution` class contains the algorithm for validating binary tree nodes using the Union-Find data structure.\n1. **validateBinaryTreeNodes Method:**\n\n - The `validateBinaryTreeNodes` method is used to check whether the given data represents a valid binary tree.\n - It iterates through the nodes and their children, and for each child, it checks if it can be joined with the current node using the `UnionFind` data structure.\n - If at any point during the iteration, it finds a situation where joining is not possible (indicating a cycle or multiple components), it returns `false`.\n - After iterating through all nodes, it checks if the number of components in the `UnionFind` is 1, which means all nodes are part of a single connected component, and returns `true`. Otherwise, it returns `false`.\n1. **Usage:**\n\n- The code can be used to validate whether the given data, represented by `leftChild` and `rightChild` vectors, forms a valid binary tree or not.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass UnionFind { \npublic:\n int components;\n int n;\n vector<int> parents;\n\n UnionFind(int n) {\n this->n = n;\n parents = vector(n, 0);\n components = n;\n \n for (int i = 0; i < n; i++) {\n parents[i] = i;\n }\n }\n \n bool join(int parent, int child) {\n int parentParent = find(parent);\n int childParent = find(child);\n \n if (childParent != child || parentParent == childParent) {\n return false;\n }\n \n components--;\n parents[childParent] = parentParent;\n return true;\n }\n \n int find(int node) {\n if (parents[node] != node) {\n parents[node] = find(parents[node]);\n }\n \n return parents[node];\n }\n};\n\nclass Solution {\npublic:\n bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {\n UnionFind uf(n);\n for (int node = 0; node < n; node++) {\n int children[] = {leftChild[node], rightChild[node]};\n for (int child : children) {\n if (child == -1) {\n continue;\n }\n \n if (!uf.join(node, child)) {\n return false;\n }\n }\n }\n \n return uf.components == 1;\n }\n};\n```\n\n\n```C []\n\ntypedef struct UnionFind {\n int components;\n int n;\n int* parents;\n} UnionFind;\n\nUnionFind* createUnionFind(int n) {\n UnionFind* uf = (UnionFind*)malloc(sizeof(UnionFind));\n uf->n = n;\n uf->parents = (int*)malloc(n * sizeof(int));\n uf->components = n;\n\n for (int i = 0; i < n; i++) {\n uf->parents[i] = i;\n }\n\n return uf;\n}\n\nint find(UnionFind* uf, int node) {\n if (uf->parents[node] != node) {\n uf->parents[node] = find(uf, uf->parents[node]);\n }\n\n return uf->parents[node];\n}\n\nbool join(UnionFind* uf, int parent, int child) {\n int parentParent = find(uf, parent);\n int childParent = find(uf, child);\n\n if (childParent != child || parentParent == childParent) {\n return false;\n }\n\n uf->components--;\n uf->parents[childParent] = parentParent;\n return true;\n}\n\nvoid destroyUnionFind(UnionFind* uf) {\n free(uf->parents);\n free(uf);\n}\n\nbool validateBinaryTreeNodes(int n, int* leftChild, int* rightChild) {\n UnionFind* uf = createUnionFind(n);\n\n for (int node = 0; node < n; node++) {\n int children[] = {leftChild[node], rightChild[node]};\n\n for (int i = 0; i < 2; i++) {\n int child = children[i];\n if (child == -1) {\n continue;\n }\n\n if (!join(uf, node, child)) {\n destroyUnionFind(uf);\n return false;\n }\n }\n }\n\n bool result = (uf->components == 1);\n destroyUnionFind(uf);\n\n return result;\n}\n\n```\n\n```Java []\nclass UnionFind {\n private final int n;\n private final int[] parents;\n public int components;\n \n UnionFind(int n) {\n this.n = n;\n parents = new int[n];\n components = n;\n \n for (int i = 0; i < n; i++) {\n parents[i] = i;\n }\n }\n \n public boolean union(int parent, int child) {\n int parentParent = find(parent);\n int childParent = find(child);\n \n if (childParent != child || parentParent == childParent) {\n return false;\n }\n \n components--;\n parents[childParent] = parentParent;\n return true;\n }\n \n private int find(int node) {\n if (parents[node] != node) {\n parents[node] = find(parents[node]);\n }\n \n return parents[node];\n }\n}\n\nclass Solution {\n public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {\n UnionFind uf = new UnionFind(n);\n for (int node = 0; node < n; node++) {\n int[] children = {leftChild[node], rightChild[node]};\n for (int child : children) {\n if (child == -1) {\n continue;\n }\n \n if (!uf.union(node, child)) {\n return false;\n }\n }\n }\n \n return uf.components == 1;\n }\n}\n\n```\n\n```python3 []\nclass UnionFind:\n def __init__(self, n):\n self.components = n\n self.parents = list(range(n))\n \n def union(self, parent, child):\n parent_parent = self.find(parent)\n child_parent = self.find(child)\n \n if child_parent != child or parent_parent == child_parent:\n return False\n \n self.components -= 1\n self.parents[child_parent] = parent_parent\n return True\n\n def find(self, node):\n if self.parents[node] != node:\n self.parents[node] = self.find(self.parents[node])\n \n return self.parents[node]\n \n\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n uf = UnionFind(n)\n for node in range(n):\n for child in [leftChild[node], rightChild[node]]:\n if child == -1:\n continue\n\n if not uf.union(node, child):\n return False\n \n return uf.components == 1\n\n```\n\n```javascript []\nclass UnionFind {\n constructor(n) {\n this.components = n;\n this.n = n;\n this.parents = new Array(n);\n\n for (let i = 0; i < n; i++) {\n this.parents[i] = i;\n }\n }\n\n join(parent, child) {\n const parentParent = this.find(parent);\n const childParent = this.find(child);\n\n if (childParent !== child || parentParent === childParent) {\n return false;\n }\n\n this.components--;\n this.parents[childParent] = parentParent;\n return true;\n }\n\n find(node) {\n if (this.parents[node] !== node) {\n this.parents[node] = this.find(this.parents[node]);\n }\n\n return this.parents[node];\n }\n}\n\nclass Solution {\n validateBinaryTreeNodes(n, leftChild, rightChild) {\n const uf = new UnionFind(n);\n\n for (let node = 0; node < n; node++) {\n const children = [leftChild[node], rightChild[node]];\n \n for (const child of children) {\n if (child === -1) {\n continue;\n }\n\n if (!uf.join(node, child)) {\n return false;\n }\n }\n }\n\n return uf.components === 1;\n }\n}\n```\n\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | You have `n` binary tree nodes numbered from `0` to `n - 1` where node `i` has two children `leftChild[i]` and `rightChild[i]`, return `true` if and only if **all** the given nodes form **exactly one** valid binary tree.
If node `i` has no left child then `leftChild[i]` will equal `-1`, similarly for the right child.
Note that the nodes have no values and that we only use the node numbers in this problem.
**Example 1:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,-1,-1,-1\]
**Output:** true
**Example 2:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,3,-1,-1\]
**Output:** false
**Example 3:**
**Input:** n = 2, leftChild = \[1,0\], rightChild = \[-1,-1\]
**Output:** false
**Constraints:**
* `n == leftChild.length == rightChild.length`
* `1 <= n <= 104`
* `-1 <= leftChild[i], rightChild[i] <= n - 1` | Can you use backtracking to solve this problem ?. Suppose you've placed a bunch of squares. Where is the natural spot to place the next square ?. The maximum number of squares to be placed will be ≤ max(n,m). |
✅☑[C++/C/Java/Python/JavaScript] || 3 Approaches || Optimized || EXPLAINED🔥 | validate-binary-tree-nodes | 0 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### *Approach 1 (DFS)*\n1. `validateBinaryTreeNodes` is the main function that takes three parameters:\n\n - `n`: The total number of nodes in the tree.\n - `leftChild`: A vector representing the left child of each node. A value of -1 means there is no left child.\n - `rightChild`: A vector representing the right child of each node. A value of -1 means there is no right child.\n1. It first calls the `findRoot` function to determine the root node of the tree. The `findRoot` function:\n\n - Initializes a set called `children` to store the children of all nodes.\n - Adds the indices of left and right children to the `children` set.\n - Iterates through indices from 0 to `n-1` to find the node that is not present in the `children` set. This node is considered the root.\n - If there\'s no unique root, the function returns -1.\n1. If there is no unique root (i.e., `root` is -1), the function returns `false` because a valid tree must have exactly one root.\n\n1. It then uses depth-first search (DFS) to traverse the tree starting from the root node:\n\n - Initializes a set `seen` to keep track of visited nodes.\n - Initializes a `stack` stack for DFS.\n - Inserts the root into the `seen` set and pushes it onto the stack.\n1. In the DFS loop:\n\n - Pops the top node from the stack.\n - Checks its left and right children (if they exist) and whether they have already been seen. If a child has been seen, this means there\'s a cycle in the tree, so the function returns `false`.\n - If a child has not been seen, it is pushed onto the stack and added to the `seen` set.\n1. After the DFS traversal, the function checks if the number of nodes in the `seen` set is equal to `n`. If it is, this means all nodes in the tree were visited without any cycles, so the tree is valid, and the function returns `true`.\n\n1. If there were any cycles or some nodes were not reachable from the root, the function returns `false`.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {\n int root = findRoot(n, leftChild, rightChild);\n if (root == -1) {\n return false;\n }\n \n unordered_set<int> seen;\n stack<int> stack;\n seen.insert(root);\n stack.push(root);\n \n while (!stack.empty()) {\n int node = stack.top();\n stack.pop();\n \n int children[] = {leftChild[node], rightChild[node]};\n for (int child : children) {\n if (child != -1) {\n if (seen.find(child) != seen.end()) {\n return false;\n }\n \n stack.push(child);\n seen.insert(child);\n }\n }\n }\n \n return seen.size() == n;\n }\n \n int findRoot(int n, vector<int>& left, vector<int>& right) {\n unordered_set<int> children;\n children.insert(left.begin(), left.end());\n children.insert(right.begin(), right.end());\n \n for (int i = 0; i < n; i++) {\n if (children.find(i) == children.end()) {\n return i;\n }\n }\n \n return -1;\n }\n};\n```\n\n\n```C []\n\nint findRoot(int n, int* left, int* right) {\n int* children = (int*)malloc(n * sizeof(int));\n if (!children) {\n return -1;\n }\n \n for (int i = 0; i < n; i++) {\n children[i] = 0;\n }\n\n for (int i = 0; i < n; i++) {\n if (left[i] != -1) {\n children[left[i]] = 1;\n }\n if (right[i] != -1) {\n children[right[i]] = 1;\n }\n }\n\n for (int i = 0; i < n; i++) {\n if (children[i] == 0) {\n free(children);\n return i;\n }\n }\n\n free(children);\n return -1;\n}\n\n// Function to validate the binary tree nodes\nbool validateBinaryTreeNodes(int n, int* leftChild, int* rightChild) {\n int root = findRoot(n, leftChild, rightChild);\n if (root == -1) {\n return false;\n }\n\n int* seen = (int*)malloc(n * sizeof(int));\n if (!seen) {\n return false;\n }\n \n for (int i = 0; i < n; i++) {\n seen[i] = 0;\n }\n\n int* stack = (int*)malloc(n * sizeof(int));\n if (!stack) {\n free(seen);\n return false;\n }\n\n int stackTop = -1;\n seen[root] = 1;\n stack[++stackTop] = root;\n\n while (stackTop >= 0) {\n int node = stack[stackTop--];\n int children[] = {leftChild[node], rightChild[node]};\n\n for (int i = 0; i < 2; i++) {\n int child = children[i];\n if (child != -1) {\n if (seen[child] == 1) {\n free(stack);\n free(seen);\n return false;\n }\n\n stack[++stackTop] = child;\n seen[child] = 1;\n }\n }\n }\n\n free(stack);\n free(seen);\n\n return true;\n}\n\n```\n\n```Java []\nclass Solution {\n public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {\n int root = findRoot(n, leftChild, rightChild);\n if (root == -1) {\n return false;\n }\n \n Set<Integer> seen = new HashSet<>();\n Stack<Integer> stack = new Stack<>();\n seen.add(root);\n stack.push(root);\n \n while (!stack.isEmpty()) {\n int node = stack.pop();\n int[] children = {leftChild[node], rightChild[node]};\n \n for (int child : children) {\n if (child != -1) {\n if (seen.contains(child)) {\n return false;\n }\n \n stack.push(child);\n seen.add(child);\n }\n }\n \n }\n \n return seen.size() == n;\n }\n \n public int findRoot(int n, int[] left, int[] right) {\n Set<Integer> children = new HashSet<>();\n for (int node : left) {\n children.add(node);\n }\n \n for (int node : right) {\n children.add(node);\n }\n \n for (int i = 0; i < n; i++) {\n if (!children.contains(i)) {\n return i;\n }\n }\n \n return -1;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n def find_root():\n children = set(leftChild) | set(rightChild)\n \n for i in range(n):\n if i not in children:\n return i\n \n return -1\n \n root = find_root()\n if root == -1:\n return False\n \n seen = {root}\n stack = [root]\n while stack:\n node = stack.pop()\n for child in [leftChild[node], rightChild[node]]:\n if child != -1:\n if child in seen:\n return False\n \n stack.append(child)\n seen.add(child)\n \n return len(seen) == n\n\n```\n\n```javascript []\nfunction findRoot(n, left, right) {\n const children = new Set();\n\n for (let i = 0; i < n; i++) {\n if (left[i] !== -1) {\n children.add(left[i]);\n }\n if (right[i] !== -1) {\n children.add(right[i]);\n }\n }\n\n for (let i = 0; i < n; i++) {\n if (!children.has(i)) {\n return i;\n }\n }\n\n return -1;\n}\n\n/**\n * Function to validate the binary tree nodes\n * @param {number} n\n * @param {number[]} leftChild\n * @param {number[]} rightChild\n * @returns {boolean}\n */\nfunction validateBinaryTreeNodes(n, leftChild, rightChild) {\n const root = findRoot(n, leftChild, rightChild);\n if (root === -1) {\n return false;\n }\n\n const seen = new Array(n).fill(0);\n const stack = [];\n seen[root] = 1;\n stack.push(root);\n\n while (stack.length > 0) {\n const node = stack.pop();\n const children = [leftChild[node], rightChild[node]];\n\n for (const child of children) {\n if (child !== -1) {\n if (seen[child] === 1) {\n return false;\n }\n stack.push(child);\n seen[child] = 1;\n }\n }\n }\n\n return true;\n}\n```\n\n\n---\n\n#### *Approach 2 (BFS)*\n1. `validateBinaryTreeNodes` function:\n\n - This function takes three arguments: `n` (the number of nodes), `leftChild` (a vector representing the left child of each node), and `rightChild` (a vector representing the right child of each node).\n - It first calls the `findRoot` function to find the root node of the binary tree.\n - If the root is not found (i.e., `findRoot` returns -1), it returns `false` because a valid binary tree must have a single root node.\n - It uses an unordered set `seen` to keep track of nodes that have been visited and a queue `queue` for breadth-first traversal.\n - The root node is marked as seen and added to the queue.\n - It enters a loop to process nodes while the queue is not empty.\n - Inside the loop, it dequeues a node from the front of the queue and checks its children.\n - It uses an array `children` to represent the left and right children of the current node.\n - For each child, if it exists (i.e., not -1) and is already seen, it returns `false` because a valid binary tree should not have any duplicate nodes.\n - If the child is valid and not seen, it enqueues the child, marks it as seen, and continues.\n - The loop continues until all nodes are processed.\n - After the loop, it checks if the number of seen nodes is equal to `n`, which indicates that all nodes were visited. If true, it returns `true`, indicating a valid binary tree.\n2. `findRoot` function:\n\n - This function is responsible for finding the root of the binary tree. It takes the same arguments as `validateBinaryTreeNodes`.\n - It uses an unordered set `children` to keep track of nodes that are children of some other node.\n - It iterates through the nodes from 0 to `n-1` and adds their values to the `children` set if they are present as children in `leftChild` or `rightChild`.\n - The first node that is not in the `children` set is considered the root, and its index is returned.\n - If no such node is found (all nodes are children), it returns -1, indicating the absence of a root.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {\n int root = findRoot(n, leftChild, rightChild);\n if (root == -1) {\n return false;\n }\n \n unordered_set<int> seen;\n queue<int> queue;\n seen.insert(root);\n queue.push(root);\n \n while (!queue.empty()) {\n int node = queue.front();\n queue.pop();\n \n int children[] = {leftChild[node], rightChild[node]};\n for (int child : children) {\n if (child != -1) {\n if (seen.find(child) != seen.end()) {\n return false;\n }\n \n queue.push(child);\n seen.insert(child);\n }\n }\n }\n \n return seen.size() == n;\n }\n \n int findRoot(int n, vector<int>& left, vector<int>& right) {\n unordered_set<int> children;\n children.insert(left.begin(), left.end());\n children.insert(right.begin(), right.end());\n \n for (int i = 0; i < n; i++) {\n if (children.find(i) == children.end()) {\n return i;\n }\n }\n \n return -1;\n }\n};\n```\n\n\n```C []\nbool validateBinaryTreeNodes(int n, int* leftChild, int* rightChild) {\n int root = findRoot(n, leftChild, rightChild);\n if (root == -1) {\n return false;\n }\n\n int* seen = (int*)calloc(n, sizeof(int));\n int* queue = (int*)calloc(n, sizeof(int));\n int front = 0, rear = 0;\n\n seen[root] = 1;\n queue[rear++] = root;\n\n while (front < rear) {\n int node = queue[front++];\n \n int children[2] = {leftChild[node], rightChild[node]};\n for (int i = 0; i < 2; i++) {\n int child = children[i];\n if (child != -1) {\n if (seen[child]) {\n free(seen);\n free(queue);\n return false;\n }\n\n queue[rear++] = child;\n seen[child] = 1;\n }\n }\n }\n\n free(seen);\n free(queue);\n\n return front == n;\n}\n\nint findRoot(int n, int* left, int* right) {\n int* children = (int*)calloc(n, sizeof(int));\n\n for (int i = 0; i < n; i++) {\n children[left[i]] = 1;\n children[right[i]] = 1;\n }\n\n for (int i = 0; i < n; i++) {\n if (!children[i]) {\n free(children);\n return i;\n }\n }\n\n free(children);\n return -1;\n}\n\n\n```\n\n```Java []\nclass Solution {\n public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {\n int root = findRoot(n, leftChild, rightChild);\n if (root == -1) {\n return false;\n }\n \n Set<Integer> seen = new HashSet<>();\n Queue<Integer> queue = new LinkedList<>();\n seen.add(root);\n queue.add(root);\n \n while (!queue.isEmpty()) {\n int node = queue.remove();\n int[] children = {leftChild[node], rightChild[node]};\n \n for (int child : children) {\n if (child != -1) {\n if (seen.contains(child)) {\n return false;\n }\n \n queue.add(child);\n seen.add(child);\n }\n }\n \n }\n \n return seen.size() == n;\n }\n \n public int findRoot(int n, int[] left, int[] right) {\n Set<Integer> children = new HashSet<>();\n for (int node : left) {\n children.add(node);\n }\n \n for (int node : right) {\n children.add(node);\n }\n \n for (int i = 0; i < n; i++) {\n if (!children.contains(i)) {\n return i;\n }\n }\n \n return -1;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n def find_root():\n children = set(leftChild) | set(rightChild)\n \n for i in range(n):\n if i not in children:\n return i\n \n return -1\n \n root = find_root()\n if root == -1:\n return False\n \n seen = {root}\n queue = deque([root])\n while queue:\n node = queue.popleft()\n for child in [leftChild[node], rightChild[node]]:\n if child != -1:\n if child in seen:\n return False\n \n queue.append(child)\n seen.add(child)\n \n return len(seen) == n\n\n```\n\n```javascript []\nfunction validateBinaryTreeNodes(n, leftChild, rightChild) {\n const root = findRoot(n, leftChild, rightChild);\n if (root === -1) {\n return false;\n }\n\n const seen = new Set();\n const queue = [];\n seen.add(root);\n queue.push(root);\n\n while (queue.length > 0) {\n const node = queue.shift();\n\n const children = [leftChild[node], rightChild[node]];\n for (const child of children) {\n if (child !== -1) {\n if (seen.has(child)) {\n return false;\n }\n\n queue.push(child);\n seen.add(child);\n }\n }\n }\n\n return seen.size === n;\n}\n\nfunction findRoot(n, left, right) {\n const children = new Set();\n for (let i = 0; i < n; i++) {\n children.add(left[i]);\n children.add(right[i]);\n }\n\n for (let i = 0; i < n; i++) {\n if (!children.has(i)) {\n return i;\n }\n }\n\n return -1;\n}\n\n```\n\n\n---\n#### *Approach 3 (Union Find)*\n1. **Union-Find (Disjoint Set) Data Structure:**\n\n - A Union-Find data structure is used for efficiently handling sets of elements and checking for connectivity among them.\n1. **UnionFind Class:**\n\n - The `UnionFind` class is defined to represent a disjoint-set data structure.\n - It keeps track of the number of components (connected sets) and the parents (representatives) of individual elements.\n - The `UnionFind` constructor initializes the data structure with \'n\' elements, where each element is its own parent, and there are initially \'n\' components.\n1. **join Method:**\n\n - The `join` method is used to combine two elements (nodes) if they are not already part of the same component. It checks whether the parent of the child is the same as the child (indicating it\'s the representative) and whether the parent of the parent is the same as the child (indicating they are already part of the same component).\n - If they meet these criteria, it means they are part of the same component and should not be joined, so it returns `false`. Otherwise, it performs the union operation by making the parent of the child\'s parent the same as the parent, effectively joining the two components. It also decrements the component count.\n1. **find Method:**\n\n - The `find` method returns the representative (parent) of a given element. It utilizes path compression, which means that while finding the parent, it also updates the parent of the current element to the representative. This helps in optimizing future find operations.\n1. **Solution Class:**\n\n - The `Solution` class contains the algorithm for validating binary tree nodes using the Union-Find data structure.\n1. **validateBinaryTreeNodes Method:**\n\n - The `validateBinaryTreeNodes` method is used to check whether the given data represents a valid binary tree.\n - It iterates through the nodes and their children, and for each child, it checks if it can be joined with the current node using the `UnionFind` data structure.\n - If at any point during the iteration, it finds a situation where joining is not possible (indicating a cycle or multiple components), it returns `false`.\n - After iterating through all nodes, it checks if the number of components in the `UnionFind` is 1, which means all nodes are part of a single connected component, and returns `true`. Otherwise, it returns `false`.\n1. **Usage:**\n\n- The code can be used to validate whether the given data, represented by `leftChild` and `rightChild` vectors, forms a valid binary tree or not.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass UnionFind { \npublic:\n int components;\n int n;\n vector<int> parents;\n\n UnionFind(int n) {\n this->n = n;\n parents = vector(n, 0);\n components = n;\n \n for (int i = 0; i < n; i++) {\n parents[i] = i;\n }\n }\n \n bool join(int parent, int child) {\n int parentParent = find(parent);\n int childParent = find(child);\n \n if (childParent != child || parentParent == childParent) {\n return false;\n }\n \n components--;\n parents[childParent] = parentParent;\n return true;\n }\n \n int find(int node) {\n if (parents[node] != node) {\n parents[node] = find(parents[node]);\n }\n \n return parents[node];\n }\n};\n\nclass Solution {\npublic:\n bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {\n UnionFind uf(n);\n for (int node = 0; node < n; node++) {\n int children[] = {leftChild[node], rightChild[node]};\n for (int child : children) {\n if (child == -1) {\n continue;\n }\n \n if (!uf.join(node, child)) {\n return false;\n }\n }\n }\n \n return uf.components == 1;\n }\n};\n```\n\n\n```C []\n\ntypedef struct UnionFind {\n int components;\n int n;\n int* parents;\n} UnionFind;\n\nUnionFind* createUnionFind(int n) {\n UnionFind* uf = (UnionFind*)malloc(sizeof(UnionFind));\n uf->n = n;\n uf->parents = (int*)malloc(n * sizeof(int));\n uf->components = n;\n\n for (int i = 0; i < n; i++) {\n uf->parents[i] = i;\n }\n\n return uf;\n}\n\nint find(UnionFind* uf, int node) {\n if (uf->parents[node] != node) {\n uf->parents[node] = find(uf, uf->parents[node]);\n }\n\n return uf->parents[node];\n}\n\nbool join(UnionFind* uf, int parent, int child) {\n int parentParent = find(uf, parent);\n int childParent = find(uf, child);\n\n if (childParent != child || parentParent == childParent) {\n return false;\n }\n\n uf->components--;\n uf->parents[childParent] = parentParent;\n return true;\n}\n\nvoid destroyUnionFind(UnionFind* uf) {\n free(uf->parents);\n free(uf);\n}\n\nbool validateBinaryTreeNodes(int n, int* leftChild, int* rightChild) {\n UnionFind* uf = createUnionFind(n);\n\n for (int node = 0; node < n; node++) {\n int children[] = {leftChild[node], rightChild[node]};\n\n for (int i = 0; i < 2; i++) {\n int child = children[i];\n if (child == -1) {\n continue;\n }\n\n if (!join(uf, node, child)) {\n destroyUnionFind(uf);\n return false;\n }\n }\n }\n\n bool result = (uf->components == 1);\n destroyUnionFind(uf);\n\n return result;\n}\n\n```\n\n```Java []\nclass UnionFind {\n private final int n;\n private final int[] parents;\n public int components;\n \n UnionFind(int n) {\n this.n = n;\n parents = new int[n];\n components = n;\n \n for (int i = 0; i < n; i++) {\n parents[i] = i;\n }\n }\n \n public boolean union(int parent, int child) {\n int parentParent = find(parent);\n int childParent = find(child);\n \n if (childParent != child || parentParent == childParent) {\n return false;\n }\n \n components--;\n parents[childParent] = parentParent;\n return true;\n }\n \n private int find(int node) {\n if (parents[node] != node) {\n parents[node] = find(parents[node]);\n }\n \n return parents[node];\n }\n}\n\nclass Solution {\n public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {\n UnionFind uf = new UnionFind(n);\n for (int node = 0; node < n; node++) {\n int[] children = {leftChild[node], rightChild[node]};\n for (int child : children) {\n if (child == -1) {\n continue;\n }\n \n if (!uf.union(node, child)) {\n return false;\n }\n }\n }\n \n return uf.components == 1;\n }\n}\n\n```\n\n```python3 []\nclass UnionFind:\n def __init__(self, n):\n self.components = n\n self.parents = list(range(n))\n \n def union(self, parent, child):\n parent_parent = self.find(parent)\n child_parent = self.find(child)\n \n if child_parent != child or parent_parent == child_parent:\n return False\n \n self.components -= 1\n self.parents[child_parent] = parent_parent\n return True\n\n def find(self, node):\n if self.parents[node] != node:\n self.parents[node] = self.find(self.parents[node])\n \n return self.parents[node]\n \n\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n uf = UnionFind(n)\n for node in range(n):\n for child in [leftChild[node], rightChild[node]]:\n if child == -1:\n continue\n\n if not uf.union(node, child):\n return False\n \n return uf.components == 1\n\n```\n\n```javascript []\nclass UnionFind {\n constructor(n) {\n this.components = n;\n this.n = n;\n this.parents = new Array(n);\n\n for (let i = 0; i < n; i++) {\n this.parents[i] = i;\n }\n }\n\n join(parent, child) {\n const parentParent = this.find(parent);\n const childParent = this.find(child);\n\n if (childParent !== child || parentParent === childParent) {\n return false;\n }\n\n this.components--;\n this.parents[childParent] = parentParent;\n return true;\n }\n\n find(node) {\n if (this.parents[node] !== node) {\n this.parents[node] = this.find(this.parents[node]);\n }\n\n return this.parents[node];\n }\n}\n\nclass Solution {\n validateBinaryTreeNodes(n, leftChild, rightChild) {\n const uf = new UnionFind(n);\n\n for (let node = 0; node < n; node++) {\n const children = [leftChild[node], rightChild[node]];\n \n for (const child of children) {\n if (child === -1) {\n continue;\n }\n\n if (!uf.join(node, child)) {\n return false;\n }\n }\n }\n\n return uf.components === 1;\n }\n}\n```\n\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
Easy & Explained Graph (Dfs) Solution Python3 || Python Solution | validate-binary-tree-nodes | 0 | 1 | # Intuition- and Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nBasic intution to approach this problem would be like when only one binary tree is possible:\n- There should be a root node which means a node which only have max two outgoing edges not any incoming edge.\n- Should not have cycle inside the tree.\n- Two nodes cannot point to a single node.\n\nTo create such solution \n- first we will create an graph data structure. i have created here using hashmap/dictionary. \n- after creating graph during creation we will try to find root node by checking which element does not have an incoming node and in case there are multiple or no nodes that means we can\'t create binary tree form them.\n- Now once we find the root we will run the dfs and check if node is visited twice then no we can\'t create the binary tree else add those node to visited set.\n- if we were able to traverse all the node without revisting and all nodes are visited that means we can create the binary tree.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n graph = defaultdict(list)\n temp = {}\n for i in range(n):\n temp[i] = 1\n\n for i in range(n):\n if(leftChild[i]!=-1):\n graph[i].append(leftChild[i])\n if(leftChild[i] in temp):\n del temp[leftChild[i]]\n if(rightChild[i]!=-1):\n graph[i].append(rightChild[i])\n if(rightChild[i] in temp):\n del temp[rightChild[i]]\n\n if(len(temp)!=1):\n return False\n\n for key in temp.keys():\n root = key\n\n def dfs(node):\n if(node in visited):\n return False\n ans = True\n visited[node] = 1\n for child in graph[node]:\n ans = ans and dfs(child)\n return ans\n\n visited = {}\n ans = dfs(root)\n if(ans and len(visited)==n):\n return True\n return False\n``` | 1 | You have `n` binary tree nodes numbered from `0` to `n - 1` where node `i` has two children `leftChild[i]` and `rightChild[i]`, return `true` if and only if **all** the given nodes form **exactly one** valid binary tree.
If node `i` has no left child then `leftChild[i]` will equal `-1`, similarly for the right child.
Note that the nodes have no values and that we only use the node numbers in this problem.
**Example 1:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,-1,-1,-1\]
**Output:** true
**Example 2:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,3,-1,-1\]
**Output:** false
**Example 3:**
**Input:** n = 2, leftChild = \[1,0\], rightChild = \[-1,-1\]
**Output:** false
**Constraints:**
* `n == leftChild.length == rightChild.length`
* `1 <= n <= 104`
* `-1 <= leftChild[i], rightChild[i] <= n - 1` | Can you use backtracking to solve this problem ?. Suppose you've placed a bunch of squares. Where is the natural spot to place the next square ?. The maximum number of squares to be placed will be ≤ max(n,m). |
Easy & Explained Graph (Dfs) Solution Python3 || Python Solution | validate-binary-tree-nodes | 0 | 1 | # Intuition- and Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nBasic intution to approach this problem would be like when only one binary tree is possible:\n- There should be a root node which means a node which only have max two outgoing edges not any incoming edge.\n- Should not have cycle inside the tree.\n- Two nodes cannot point to a single node.\n\nTo create such solution \n- first we will create an graph data structure. i have created here using hashmap/dictionary. \n- after creating graph during creation we will try to find root node by checking which element does not have an incoming node and in case there are multiple or no nodes that means we can\'t create binary tree form them.\n- Now once we find the root we will run the dfs and check if node is visited twice then no we can\'t create the binary tree else add those node to visited set.\n- if we were able to traverse all the node without revisting and all nodes are visited that means we can create the binary tree.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n graph = defaultdict(list)\n temp = {}\n for i in range(n):\n temp[i] = 1\n\n for i in range(n):\n if(leftChild[i]!=-1):\n graph[i].append(leftChild[i])\n if(leftChild[i] in temp):\n del temp[leftChild[i]]\n if(rightChild[i]!=-1):\n graph[i].append(rightChild[i])\n if(rightChild[i] in temp):\n del temp[rightChild[i]]\n\n if(len(temp)!=1):\n return False\n\n for key in temp.keys():\n root = key\n\n def dfs(node):\n if(node in visited):\n return False\n ans = True\n visited[node] = 1\n for child in graph[node]:\n ans = ans and dfs(child)\n return ans\n\n visited = {}\n ans = dfs(root)\n if(ans and len(visited)==n):\n return True\n return False\n``` | 1 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
Python3 Solution | validate-binary-tree-nodes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n parent={}\n for p,child in enumerate(zip(leftChild,rightChild)):\n for c in child:\n if c==-1:\n continue \n if c in parent:\n return False \n if p in parent and parent[p]==c:\n return False \n parent[c]=p\n root=set(range(n))-set(parent.keys())\n if len(root)!=1:\n return False \n def count(root):\n if root ==-1:\n return 0\n return 1+count(leftChild[root])+count(rightChild[root])\n return count(root.pop())==n\n\n \n``` | 2 | You have `n` binary tree nodes numbered from `0` to `n - 1` where node `i` has two children `leftChild[i]` and `rightChild[i]`, return `true` if and only if **all** the given nodes form **exactly one** valid binary tree.
If node `i` has no left child then `leftChild[i]` will equal `-1`, similarly for the right child.
Note that the nodes have no values and that we only use the node numbers in this problem.
**Example 1:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,-1,-1,-1\]
**Output:** true
**Example 2:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,3,-1,-1\]
**Output:** false
**Example 3:**
**Input:** n = 2, leftChild = \[1,0\], rightChild = \[-1,-1\]
**Output:** false
**Constraints:**
* `n == leftChild.length == rightChild.length`
* `1 <= n <= 104`
* `-1 <= leftChild[i], rightChild[i] <= n - 1` | Can you use backtracking to solve this problem ?. Suppose you've placed a bunch of squares. Where is the natural spot to place the next square ?. The maximum number of squares to be placed will be ≤ max(n,m). |
Python3 Solution | validate-binary-tree-nodes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n parent={}\n for p,child in enumerate(zip(leftChild,rightChild)):\n for c in child:\n if c==-1:\n continue \n if c in parent:\n return False \n if p in parent and parent[p]==c:\n return False \n parent[c]=p\n root=set(range(n))-set(parent.keys())\n if len(root)!=1:\n return False \n def count(root):\n if root ==-1:\n return 0\n return 1+count(leftChild[root])+count(rightChild[root])\n return count(root.pop())==n\n\n \n``` | 2 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
O(n), Shortest, nice and clear run through nodes with marking parents and roots. | validate-binary-tree-nodes | 0 | 1 | # Approach\nNice and clear single run through nodes with marking parents and roots. \n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n parent = [-1] * n\n root = list(range(n))\n\n for i, children in enumerate(zip(leftChild, rightChild)):\n for child in children:\n if child == -1:\n continue\n if root[child] == root[i] or parent[child] != -1:\n return False\n \n parent[child] = i\n root[child] = root[i]\n \n return parent.count(-1) == 1\n``` | 1 | You have `n` binary tree nodes numbered from `0` to `n - 1` where node `i` has two children `leftChild[i]` and `rightChild[i]`, return `true` if and only if **all** the given nodes form **exactly one** valid binary tree.
If node `i` has no left child then `leftChild[i]` will equal `-1`, similarly for the right child.
Note that the nodes have no values and that we only use the node numbers in this problem.
**Example 1:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,-1,-1,-1\]
**Output:** true
**Example 2:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,3,-1,-1\]
**Output:** false
**Example 3:**
**Input:** n = 2, leftChild = \[1,0\], rightChild = \[-1,-1\]
**Output:** false
**Constraints:**
* `n == leftChild.length == rightChild.length`
* `1 <= n <= 104`
* `-1 <= leftChild[i], rightChild[i] <= n - 1` | Can you use backtracking to solve this problem ?. Suppose you've placed a bunch of squares. Where is the natural spot to place the next square ?. The maximum number of squares to be placed will be ≤ max(n,m). |
O(n), Shortest, nice and clear run through nodes with marking parents and roots. | validate-binary-tree-nodes | 0 | 1 | # Approach\nNice and clear single run through nodes with marking parents and roots. \n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n parent = [-1] * n\n root = list(range(n))\n\n for i, children in enumerate(zip(leftChild, rightChild)):\n for child in children:\n if child == -1:\n continue\n if root[child] == root[i] or parent[child] != -1:\n return False\n \n parent[child] = i\n root[child] = root[i]\n \n return parent.count(-1) == 1\n``` | 1 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
✅ 80% 🔥Easy Solution 🔥With Explanation | validate-binary-tree-nodes | 0 | 1 | \n# Approach\n\nA binary tree is valid if it satisfies the following conditions:\n1. It has a single root node.\n2. Each non-root node has exactly one parent node.\n3. The tree is connected, meaning all nodes are reachable from the root.\n4. There are no cycles in the tree.\n\n# Complexity\n- Time complexity:\n O(n)\n\n- Space complexity:\n O(n)\n# Code\n```\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n indegree = [0] * n\n\n for u in range(n):\n for child in (leftChild[u], rightChild[u]):\n if child != -1: indegree[child] += 1 \n\n \n q = [u for u in range(n) if not indegree[u]]\n\n print(q)\n\n if len(q) != 1: return False\n\n vis = [False] * n\n vis[q[0]] = True\n\n for u in q:\n for v in (leftChild[u], rightChild[u]):\n if v == -1: continue\n if vis[v]: return False\n vis[v] = True\n q.append(v)\n \n\n return all(vis)\n```\n\n-----\n\n\n | 1 | You have `n` binary tree nodes numbered from `0` to `n - 1` where node `i` has two children `leftChild[i]` and `rightChild[i]`, return `true` if and only if **all** the given nodes form **exactly one** valid binary tree.
If node `i` has no left child then `leftChild[i]` will equal `-1`, similarly for the right child.
Note that the nodes have no values and that we only use the node numbers in this problem.
**Example 1:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,-1,-1,-1\]
**Output:** true
**Example 2:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,3,-1,-1\]
**Output:** false
**Example 3:**
**Input:** n = 2, leftChild = \[1,0\], rightChild = \[-1,-1\]
**Output:** false
**Constraints:**
* `n == leftChild.length == rightChild.length`
* `1 <= n <= 104`
* `-1 <= leftChild[i], rightChild[i] <= n - 1` | Can you use backtracking to solve this problem ?. Suppose you've placed a bunch of squares. Where is the natural spot to place the next square ?. The maximum number of squares to be placed will be ≤ max(n,m). |
✅ 80% 🔥Easy Solution 🔥With Explanation | validate-binary-tree-nodes | 0 | 1 | \n# Approach\n\nA binary tree is valid if it satisfies the following conditions:\n1. It has a single root node.\n2. Each non-root node has exactly one parent node.\n3. The tree is connected, meaning all nodes are reachable from the root.\n4. There are no cycles in the tree.\n\n# Complexity\n- Time complexity:\n O(n)\n\n- Space complexity:\n O(n)\n# Code\n```\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n indegree = [0] * n\n\n for u in range(n):\n for child in (leftChild[u], rightChild[u]):\n if child != -1: indegree[child] += 1 \n\n \n q = [u for u in range(n) if not indegree[u]]\n\n print(q)\n\n if len(q) != 1: return False\n\n vis = [False] * n\n vis[q[0]] = True\n\n for u in q:\n for v in (leftChild[u], rightChild[u]):\n if v == -1: continue\n if vis[v]: return False\n vis[v] = True\n q.append(v)\n \n\n return all(vis)\n```\n\n-----\n\n\n | 1 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
Python 3, topological sort | validate-binary-tree-nodes | 0 | 1 | # Intuition\nConsider the requirements needed for a valid binary tree\n\n1. At most two children for each node. (already satisfied)\n2. There is only one node which is the root node whose indgree is 0\n3. No cycle\n4. Indegree of each node is equal to 1.\n5. All nodes are reachable, which means the tree is fully connected.\n\nSo your task is to build a graph and check whether all requirements are satisfied.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTopological sort\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n graph = defaultdict(list)\n indeg = [0] * n\n\n for i in range(n):\n left, right = leftChild[i], rightChild[i]\n if left != -1:\n graph[i].append(left)\n indeg[left] += 1\n if right != -1:\n graph[i].append(right)\n indeg[right] += 1\n\n root = []\n for i in range(n):\n indegree = indeg[i]\n if indegree == 0:\n if root:\n return False\n root.append(i)\n elif indegree != 1:\n return False\n\n visited = set()\n while root:\n node = root.pop(0)\n if node in visited:\n return False\n visited.add(node)\n if node in graph:\n for child in graph[node]:\n indeg[child] -= 1\n if indeg[child] == 0:\n root.append(child)\n return len(visited) == n\n\n\n``` | 1 | You have `n` binary tree nodes numbered from `0` to `n - 1` where node `i` has two children `leftChild[i]` and `rightChild[i]`, return `true` if and only if **all** the given nodes form **exactly one** valid binary tree.
If node `i` has no left child then `leftChild[i]` will equal `-1`, similarly for the right child.
Note that the nodes have no values and that we only use the node numbers in this problem.
**Example 1:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,-1,-1,-1\]
**Output:** true
**Example 2:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,3,-1,-1\]
**Output:** false
**Example 3:**
**Input:** n = 2, leftChild = \[1,0\], rightChild = \[-1,-1\]
**Output:** false
**Constraints:**
* `n == leftChild.length == rightChild.length`
* `1 <= n <= 104`
* `-1 <= leftChild[i], rightChild[i] <= n - 1` | Can you use backtracking to solve this problem ?. Suppose you've placed a bunch of squares. Where is the natural spot to place the next square ?. The maximum number of squares to be placed will be ≤ max(n,m). |
Python 3, topological sort | validate-binary-tree-nodes | 0 | 1 | # Intuition\nConsider the requirements needed for a valid binary tree\n\n1. At most two children for each node. (already satisfied)\n2. There is only one node which is the root node whose indgree is 0\n3. No cycle\n4. Indegree of each node is equal to 1.\n5. All nodes are reachable, which means the tree is fully connected.\n\nSo your task is to build a graph and check whether all requirements are satisfied.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTopological sort\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n graph = defaultdict(list)\n indeg = [0] * n\n\n for i in range(n):\n left, right = leftChild[i], rightChild[i]\n if left != -1:\n graph[i].append(left)\n indeg[left] += 1\n if right != -1:\n graph[i].append(right)\n indeg[right] += 1\n\n root = []\n for i in range(n):\n indegree = indeg[i]\n if indegree == 0:\n if root:\n return False\n root.append(i)\n elif indegree != 1:\n return False\n\n visited = set()\n while root:\n node = root.pop(0)\n if node in visited:\n return False\n visited.add(node)\n if node in graph:\n for child in graph[node]:\n indeg[child] -= 1\n if indeg[child] == 0:\n root.append(child)\n return len(visited) == n\n\n\n``` | 1 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
[python3] find root and bfs | validate-binary-tree-nodes | 0 | 1 | Find the root of the tree first and then traverse. \nIf the visited node count == n and does not visit same node twice return True\n\n```\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n # construct a binary tree\n s = [0]\n visited = defaultdict(bool)\n \n for i in range(n):\n if leftChild[i] == s[0] or rightChild[i] == s[0]:\n s[0] = i\n \n while s:\n node = s.pop(0)\n \n if visited[node]: \n return False\n \n n -= 1\n visited[node] = True\n \n if leftChild[node] != -1:\n s.append(leftChild[node])\n if rightChild[node] != -1:\n s.append(rightChild[node])\n \n return n == 0\n \n | 1 | You have `n` binary tree nodes numbered from `0` to `n - 1` where node `i` has two children `leftChild[i]` and `rightChild[i]`, return `true` if and only if **all** the given nodes form **exactly one** valid binary tree.
If node `i` has no left child then `leftChild[i]` will equal `-1`, similarly for the right child.
Note that the nodes have no values and that we only use the node numbers in this problem.
**Example 1:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,-1,-1,-1\]
**Output:** true
**Example 2:**
**Input:** n = 4, leftChild = \[1,-1,3,-1\], rightChild = \[2,3,-1,-1\]
**Output:** false
**Example 3:**
**Input:** n = 2, leftChild = \[1,0\], rightChild = \[-1,-1\]
**Output:** false
**Constraints:**
* `n == leftChild.length == rightChild.length`
* `1 <= n <= 104`
* `-1 <= leftChild[i], rightChild[i] <= n - 1` | Can you use backtracking to solve this problem ?. Suppose you've placed a bunch of squares. Where is the natural spot to place the next square ?. The maximum number of squares to be placed will be ≤ max(n,m). |
[python3] find root and bfs | validate-binary-tree-nodes | 0 | 1 | Find the root of the tree first and then traverse. \nIf the visited node count == n and does not visit same node twice return True\n\n```\nclass Solution:\n def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:\n # construct a binary tree\n s = [0]\n visited = defaultdict(bool)\n \n for i in range(n):\n if leftChild[i] == s[0] or rightChild[i] == s[0]:\n s[0] = i\n \n while s:\n node = s.pop(0)\n \n if visited[node]: \n return False\n \n n -= 1\n visited[node] = True\n \n if leftChild[node] != -1:\n s.append(leftChild[node])\n if rightChild[node] != -1:\n s.append(rightChild[node])\n \n return n == 0\n \n | 1 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
Greedy - beat 100% time / memory | closest-divisors | 0 | 1 | The greedy principle is used in the following two aspects, so that we can immediately return once we find a candidate `i` that meets the requirment:\n\n* Iterate candidates from `int(sqrt(num+2))` to `1`.\n* Check `num + 1` before `num + 2`. Because when a candidate `i` is valid for both `num + 1` and `num + 2`, The diff value of the former is smaller. e.g. `num = 1`.\n\n```python\n def closestDivisors(self, num: int) -> List[int]:\n for i in reversed(range(1, int((num + 2) ** 0.5) + 1)):\n if not (num + 1) % i:\n return [i, (num + 1) // i]\n if not (num + 2) % i:\n return [i, (num + 2) // i]\n``` | 10 | Given an integer `num`, find the closest two integers in absolute difference whose product equals `num + 1` or `num + 2`.
Return the two integers in any order.
**Example 1:**
**Input:** num = 8
**Output:** \[3,3\]
**Explanation:** For num + 1 = 9, the closest divisors are 3 & 3, for num + 2 = 10, the closest divisors are 2 & 5, hence 3 & 3 is chosen.
**Example 2:**
**Input:** num = 123
**Output:** \[5,25\]
**Example 3:**
**Input:** num = 999
**Output:** \[40,25\]
**Constraints:**
* `1 <= num <= 10^9` | Let f(n) denote the probability of the n-th person getting correct seat in n-person case, then:
f(1) = 1 (base case, trivial)
f(2) = 1/2 (also trivial) Try to calculate f(3), f(4), and f(5) using the base cases. What if the value of them?
f(i) for i >= 2 will also be 1/2. Try to proof why f(i) = 1/2 for i >= 2. |
Greedy - beat 100% time / memory | closest-divisors | 0 | 1 | The greedy principle is used in the following two aspects, so that we can immediately return once we find a candidate `i` that meets the requirment:\n\n* Iterate candidates from `int(sqrt(num+2))` to `1`.\n* Check `num + 1` before `num + 2`. Because when a candidate `i` is valid for both `num + 1` and `num + 2`, The diff value of the former is smaller. e.g. `num = 1`.\n\n```python\n def closestDivisors(self, num: int) -> List[int]:\n for i in reversed(range(1, int((num + 2) ** 0.5) + 1)):\n if not (num + 1) % i:\n return [i, (num + 1) // i]\n if not (num + 2) % i:\n return [i, (num + 2) // i]\n``` | 10 | Given two integers `tomatoSlices` and `cheeseSlices`. The ingredients of different burgers are as follows:
* **Jumbo Burger:** `4` tomato slices and `1` cheese slice.
* **Small Burger:** `2` Tomato slices and `1` cheese slice.
Return `[total_jumbo, total_small]` so that the number of remaining `tomatoSlices` equal to `0` and the number of remaining `cheeseSlices` equal to `0`. If it is not possible to make the remaining `tomatoSlices` and `cheeseSlices` equal to `0` return `[]`.
**Example 1:**
**Input:** tomatoSlices = 16, cheeseSlices = 7
**Output:** \[1,6\]
**Explantion:** To make one jumbo burger and 6 small burgers we need 4\*1 + 2\*6 = 16 tomato and 1 + 6 = 7 cheese.
There will be no remaining ingredients.
**Example 2:**
**Input:** tomatoSlices = 17, cheeseSlices = 4
**Output:** \[\]
**Explantion:** There will be no way to use all ingredients to make small and jumbo burgers.
**Example 3:**
**Input:** tomatoSlices = 4, cheeseSlices = 17
**Output:** \[\]
**Explantion:** Making 1 jumbo burger there will be 16 cheese remaining and making 2 small burgers there will be 15 cheese remaining.
**Constraints:**
* `0 <= tomatoSlices, cheeseSlices <= 107` | Find the divisors of n+1 and n+2. To find the divisors of a number, you only need to iterate to the square root of that number. |
[Java/Python 3] Mod and Sqrt, O(sqrt(n)) code. | closest-divisors | 1 | 1 | ```java\n public int[] closestDivisors(int num) {\n int[] res = {1, num + 1};\n int min = num;\n for (int n : new int[]{num + 1, num + 2}) {\n int d = (int)Math.floor(Math.sqrt(n)); \n while (d > 0 && n % d != 0) {--d; }\n if (min > n / d - d) {\n min = n / d - d;\n res = new int[]{n / d, d};\n } \n }\n return res; \n }\n```\n\nThe following code inspired by /copied from **@WilmerKrisp**\n\n```java\n public int[] closestDivisors(int num) {\n for (int i = 1 + (int)Math.floor(Math.sqrt(num)); i > 1; --i) {\n if ((num + 1) % i == 0) {\n return new int[]{i, (num + 1) / i};\n }else if ((num + 2) % i == 0) {\n return new int[]{i, (num + 2) / i};\n }\n }\n return new int[]{1, num + 1};\n }\n```\n```python\n def closestDivisors(self, num: int, o=0) -> List[int]:\n for i in range(int(math.sqrt(num)) + 1, 1, -1):\n if (num + 1) % i == 0 or (o := (num + 2) % i == 0):\n return [i, (num + 1 + o) // i]\n``` | 8 | Given an integer `num`, find the closest two integers in absolute difference whose product equals `num + 1` or `num + 2`.
Return the two integers in any order.
**Example 1:**
**Input:** num = 8
**Output:** \[3,3\]
**Explanation:** For num + 1 = 9, the closest divisors are 3 & 3, for num + 2 = 10, the closest divisors are 2 & 5, hence 3 & 3 is chosen.
**Example 2:**
**Input:** num = 123
**Output:** \[5,25\]
**Example 3:**
**Input:** num = 999
**Output:** \[40,25\]
**Constraints:**
* `1 <= num <= 10^9` | Let f(n) denote the probability of the n-th person getting correct seat in n-person case, then:
f(1) = 1 (base case, trivial)
f(2) = 1/2 (also trivial) Try to calculate f(3), f(4), and f(5) using the base cases. What if the value of them?
f(i) for i >= 2 will also be 1/2. Try to proof why f(i) = 1/2 for i >= 2. |
[Java/Python 3] Mod and Sqrt, O(sqrt(n)) code. | closest-divisors | 1 | 1 | ```java\n public int[] closestDivisors(int num) {\n int[] res = {1, num + 1};\n int min = num;\n for (int n : new int[]{num + 1, num + 2}) {\n int d = (int)Math.floor(Math.sqrt(n)); \n while (d > 0 && n % d != 0) {--d; }\n if (min > n / d - d) {\n min = n / d - d;\n res = new int[]{n / d, d};\n } \n }\n return res; \n }\n```\n\nThe following code inspired by /copied from **@WilmerKrisp**\n\n```java\n public int[] closestDivisors(int num) {\n for (int i = 1 + (int)Math.floor(Math.sqrt(num)); i > 1; --i) {\n if ((num + 1) % i == 0) {\n return new int[]{i, (num + 1) / i};\n }else if ((num + 2) % i == 0) {\n return new int[]{i, (num + 2) / i};\n }\n }\n return new int[]{1, num + 1};\n }\n```\n```python\n def closestDivisors(self, num: int, o=0) -> List[int]:\n for i in range(int(math.sqrt(num)) + 1, 1, -1):\n if (num + 1) % i == 0 or (o := (num + 2) % i == 0):\n return [i, (num + 1 + o) // i]\n``` | 8 | Given two integers `tomatoSlices` and `cheeseSlices`. The ingredients of different burgers are as follows:
* **Jumbo Burger:** `4` tomato slices and `1` cheese slice.
* **Small Burger:** `2` Tomato slices and `1` cheese slice.
Return `[total_jumbo, total_small]` so that the number of remaining `tomatoSlices` equal to `0` and the number of remaining `cheeseSlices` equal to `0`. If it is not possible to make the remaining `tomatoSlices` and `cheeseSlices` equal to `0` return `[]`.
**Example 1:**
**Input:** tomatoSlices = 16, cheeseSlices = 7
**Output:** \[1,6\]
**Explantion:** To make one jumbo burger and 6 small burgers we need 4\*1 + 2\*6 = 16 tomato and 1 + 6 = 7 cheese.
There will be no remaining ingredients.
**Example 2:**
**Input:** tomatoSlices = 17, cheeseSlices = 4
**Output:** \[\]
**Explantion:** There will be no way to use all ingredients to make small and jumbo burgers.
**Example 3:**
**Input:** tomatoSlices = 4, cheeseSlices = 17
**Output:** \[\]
**Explantion:** Making 1 jumbo burger there will be 16 cheese remaining and making 2 small burgers there will be 15 cheese remaining.
**Constraints:**
* `0 <= tomatoSlices, cheeseSlices <= 107` | Find the divisors of n+1 and n+2. To find the divisors of a number, you only need to iterate to the square root of that number. |
Beats 98% runtime and 71% memory | closest-divisors | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def closestDivisors(self, num: int) -> List[int]:\n n1,n2 = num + 1,num + 2\n for e in range(int((num + 2) ** 0.5),0,-1):\n if not n1 % e:\n return [e,n1 // e]\n if not n2 % e:\n return [e,n2 // e]\n \n``` | 0 | Given an integer `num`, find the closest two integers in absolute difference whose product equals `num + 1` or `num + 2`.
Return the two integers in any order.
**Example 1:**
**Input:** num = 8
**Output:** \[3,3\]
**Explanation:** For num + 1 = 9, the closest divisors are 3 & 3, for num + 2 = 10, the closest divisors are 2 & 5, hence 3 & 3 is chosen.
**Example 2:**
**Input:** num = 123
**Output:** \[5,25\]
**Example 3:**
**Input:** num = 999
**Output:** \[40,25\]
**Constraints:**
* `1 <= num <= 10^9` | Let f(n) denote the probability of the n-th person getting correct seat in n-person case, then:
f(1) = 1 (base case, trivial)
f(2) = 1/2 (also trivial) Try to calculate f(3), f(4), and f(5) using the base cases. What if the value of them?
f(i) for i >= 2 will also be 1/2. Try to proof why f(i) = 1/2 for i >= 2. |
Beats 98% runtime and 71% memory | closest-divisors | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def closestDivisors(self, num: int) -> List[int]:\n n1,n2 = num + 1,num + 2\n for e in range(int((num + 2) ** 0.5),0,-1):\n if not n1 % e:\n return [e,n1 // e]\n if not n2 % e:\n return [e,n2 // e]\n \n``` | 0 | Given two integers `tomatoSlices` and `cheeseSlices`. The ingredients of different burgers are as follows:
* **Jumbo Burger:** `4` tomato slices and `1` cheese slice.
* **Small Burger:** `2` Tomato slices and `1` cheese slice.
Return `[total_jumbo, total_small]` so that the number of remaining `tomatoSlices` equal to `0` and the number of remaining `cheeseSlices` equal to `0`. If it is not possible to make the remaining `tomatoSlices` and `cheeseSlices` equal to `0` return `[]`.
**Example 1:**
**Input:** tomatoSlices = 16, cheeseSlices = 7
**Output:** \[1,6\]
**Explantion:** To make one jumbo burger and 6 small burgers we need 4\*1 + 2\*6 = 16 tomato and 1 + 6 = 7 cheese.
There will be no remaining ingredients.
**Example 2:**
**Input:** tomatoSlices = 17, cheeseSlices = 4
**Output:** \[\]
**Explantion:** There will be no way to use all ingredients to make small and jumbo burgers.
**Example 3:**
**Input:** tomatoSlices = 4, cheeseSlices = 17
**Output:** \[\]
**Explantion:** Making 1 jumbo burger there will be 16 cheese remaining and making 2 small burgers there will be 15 cheese remaining.
**Constraints:**
* `0 <= tomatoSlices, cheeseSlices <= 107` | Find the divisors of n+1 and n+2. To find the divisors of a number, you only need to iterate to the square root of that number. |
Python3 Clean and Concise Solution | closest-divisors | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def closestDivisors(self, num: int) -> List[int]:\n \n \n \n def f(x):\n local=[-1,-1]\n mn=inf\n \n for i in range(1,isqrt(x)+1):\n if x%i==0 and (x//i)-i < mn:\n local = [i, x//i]\n mn=min(mn,(x//i)-i)\n return local\n \n \n \n pos1=f(num+1)\n pos2=f(num+2)\n \n \n return pos1 if (pos1[1]-pos1[0]) <= (pos2[1]-pos2[0]) else pos2\n \n \n``` | 0 | Given an integer `num`, find the closest two integers in absolute difference whose product equals `num + 1` or `num + 2`.
Return the two integers in any order.
**Example 1:**
**Input:** num = 8
**Output:** \[3,3\]
**Explanation:** For num + 1 = 9, the closest divisors are 3 & 3, for num + 2 = 10, the closest divisors are 2 & 5, hence 3 & 3 is chosen.
**Example 2:**
**Input:** num = 123
**Output:** \[5,25\]
**Example 3:**
**Input:** num = 999
**Output:** \[40,25\]
**Constraints:**
* `1 <= num <= 10^9` | Let f(n) denote the probability of the n-th person getting correct seat in n-person case, then:
f(1) = 1 (base case, trivial)
f(2) = 1/2 (also trivial) Try to calculate f(3), f(4), and f(5) using the base cases. What if the value of them?
f(i) for i >= 2 will also be 1/2. Try to proof why f(i) = 1/2 for i >= 2. |
Python3 Clean and Concise Solution | closest-divisors | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def closestDivisors(self, num: int) -> List[int]:\n \n \n \n def f(x):\n local=[-1,-1]\n mn=inf\n \n for i in range(1,isqrt(x)+1):\n if x%i==0 and (x//i)-i < mn:\n local = [i, x//i]\n mn=min(mn,(x//i)-i)\n return local\n \n \n \n pos1=f(num+1)\n pos2=f(num+2)\n \n \n return pos1 if (pos1[1]-pos1[0]) <= (pos2[1]-pos2[0]) else pos2\n \n \n``` | 0 | Given two integers `tomatoSlices` and `cheeseSlices`. The ingredients of different burgers are as follows:
* **Jumbo Burger:** `4` tomato slices and `1` cheese slice.
* **Small Burger:** `2` Tomato slices and `1` cheese slice.
Return `[total_jumbo, total_small]` so that the number of remaining `tomatoSlices` equal to `0` and the number of remaining `cheeseSlices` equal to `0`. If it is not possible to make the remaining `tomatoSlices` and `cheeseSlices` equal to `0` return `[]`.
**Example 1:**
**Input:** tomatoSlices = 16, cheeseSlices = 7
**Output:** \[1,6\]
**Explantion:** To make one jumbo burger and 6 small burgers we need 4\*1 + 2\*6 = 16 tomato and 1 + 6 = 7 cheese.
There will be no remaining ingredients.
**Example 2:**
**Input:** tomatoSlices = 17, cheeseSlices = 4
**Output:** \[\]
**Explantion:** There will be no way to use all ingredients to make small and jumbo burgers.
**Example 3:**
**Input:** tomatoSlices = 4, cheeseSlices = 17
**Output:** \[\]
**Explantion:** Making 1 jumbo burger there will be 16 cheese remaining and making 2 small burgers there will be 15 cheese remaining.
**Constraints:**
* `0 <= tomatoSlices, cheeseSlices <= 107` | Find the divisors of n+1 and n+2. To find the divisors of a number, you only need to iterate to the square root of that number. |
100% beats time, easy solution python | closest-divisors | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe basic approach is to check for all divisors of the num+1 and num+2 of them the one with less absolute difference is the pair which we found first when traversing from sqrt of num+2,bcz as we go from 1 to sqrt of n, the difference between the corresponding divisors will become less.\n\nex:\nfor n=24\n(1,24) abs diff = 23\n(2,12) abs diff = 10\n(3,8) abs diff = 5\n(4,6) abs diff = 2\nSo we can observe when we traverse from sqrt(n), we will get the pair with less abs diff first.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTraverse the loop starting with sqrt(num+2) note the pair of divisor which come first for num+1, num+2. Now the pair with less abs diff among these two will be our final result.\n\n\n# Code\n```\nclass Solution:\n def closestDivisors(self, num: int) -> List[int]:\n nump1, nump2 = num + 1, num + 2\n for div in range(isqrt(num + 2), 0, -1):\n if nump1 % div == 0:\n return div, nump1 // div\n if nump2 % div == 0:\n return div, nump2 // div\n\n \n``` | 0 | Given an integer `num`, find the closest two integers in absolute difference whose product equals `num + 1` or `num + 2`.
Return the two integers in any order.
**Example 1:**
**Input:** num = 8
**Output:** \[3,3\]
**Explanation:** For num + 1 = 9, the closest divisors are 3 & 3, for num + 2 = 10, the closest divisors are 2 & 5, hence 3 & 3 is chosen.
**Example 2:**
**Input:** num = 123
**Output:** \[5,25\]
**Example 3:**
**Input:** num = 999
**Output:** \[40,25\]
**Constraints:**
* `1 <= num <= 10^9` | Let f(n) denote the probability of the n-th person getting correct seat in n-person case, then:
f(1) = 1 (base case, trivial)
f(2) = 1/2 (also trivial) Try to calculate f(3), f(4), and f(5) using the base cases. What if the value of them?
f(i) for i >= 2 will also be 1/2. Try to proof why f(i) = 1/2 for i >= 2. |
100% beats time, easy solution python | closest-divisors | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe basic approach is to check for all divisors of the num+1 and num+2 of them the one with less absolute difference is the pair which we found first when traversing from sqrt of num+2,bcz as we go from 1 to sqrt of n, the difference between the corresponding divisors will become less.\n\nex:\nfor n=24\n(1,24) abs diff = 23\n(2,12) abs diff = 10\n(3,8) abs diff = 5\n(4,6) abs diff = 2\nSo we can observe when we traverse from sqrt(n), we will get the pair with less abs diff first.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTraverse the loop starting with sqrt(num+2) note the pair of divisor which come first for num+1, num+2. Now the pair with less abs diff among these two will be our final result.\n\n\n# Code\n```\nclass Solution:\n def closestDivisors(self, num: int) -> List[int]:\n nump1, nump2 = num + 1, num + 2\n for div in range(isqrt(num + 2), 0, -1):\n if nump1 % div == 0:\n return div, nump1 // div\n if nump2 % div == 0:\n return div, nump2 // div\n\n \n``` | 0 | Given two integers `tomatoSlices` and `cheeseSlices`. The ingredients of different burgers are as follows:
* **Jumbo Burger:** `4` tomato slices and `1` cheese slice.
* **Small Burger:** `2` Tomato slices and `1` cheese slice.
Return `[total_jumbo, total_small]` so that the number of remaining `tomatoSlices` equal to `0` and the number of remaining `cheeseSlices` equal to `0`. If it is not possible to make the remaining `tomatoSlices` and `cheeseSlices` equal to `0` return `[]`.
**Example 1:**
**Input:** tomatoSlices = 16, cheeseSlices = 7
**Output:** \[1,6\]
**Explantion:** To make one jumbo burger and 6 small burgers we need 4\*1 + 2\*6 = 16 tomato and 1 + 6 = 7 cheese.
There will be no remaining ingredients.
**Example 2:**
**Input:** tomatoSlices = 17, cheeseSlices = 4
**Output:** \[\]
**Explantion:** There will be no way to use all ingredients to make small and jumbo burgers.
**Example 3:**
**Input:** tomatoSlices = 4, cheeseSlices = 17
**Output:** \[\]
**Explantion:** Making 1 jumbo burger there will be 16 cheese remaining and making 2 small burgers there will be 15 cheese remaining.
**Constraints:**
* `0 <= tomatoSlices, cheeseSlices <= 107` | Find the divisors of n+1 and n+2. To find the divisors of a number, you only need to iterate to the square root of that number. |
python solution | closest-divisors | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def closestDivisors(self, num: int) -> List[int]:\n for i in range(int(math.sqrt(num))+1,0,-1):\n if (num+1)%i==0:\n return [i,(num+1)//i]\n if (num+2)%i==0:\n return [i,(num+2)//i]\n\n``` | 0 | Given an integer `num`, find the closest two integers in absolute difference whose product equals `num + 1` or `num + 2`.
Return the two integers in any order.
**Example 1:**
**Input:** num = 8
**Output:** \[3,3\]
**Explanation:** For num + 1 = 9, the closest divisors are 3 & 3, for num + 2 = 10, the closest divisors are 2 & 5, hence 3 & 3 is chosen.
**Example 2:**
**Input:** num = 123
**Output:** \[5,25\]
**Example 3:**
**Input:** num = 999
**Output:** \[40,25\]
**Constraints:**
* `1 <= num <= 10^9` | Let f(n) denote the probability of the n-th person getting correct seat in n-person case, then:
f(1) = 1 (base case, trivial)
f(2) = 1/2 (also trivial) Try to calculate f(3), f(4), and f(5) using the base cases. What if the value of them?
f(i) for i >= 2 will also be 1/2. Try to proof why f(i) = 1/2 for i >= 2. |
python solution | closest-divisors | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def closestDivisors(self, num: int) -> List[int]:\n for i in range(int(math.sqrt(num))+1,0,-1):\n if (num+1)%i==0:\n return [i,(num+1)//i]\n if (num+2)%i==0:\n return [i,(num+2)//i]\n\n``` | 0 | Given two integers `tomatoSlices` and `cheeseSlices`. The ingredients of different burgers are as follows:
* **Jumbo Burger:** `4` tomato slices and `1` cheese slice.
* **Small Burger:** `2` Tomato slices and `1` cheese slice.
Return `[total_jumbo, total_small]` so that the number of remaining `tomatoSlices` equal to `0` and the number of remaining `cheeseSlices` equal to `0`. If it is not possible to make the remaining `tomatoSlices` and `cheeseSlices` equal to `0` return `[]`.
**Example 1:**
**Input:** tomatoSlices = 16, cheeseSlices = 7
**Output:** \[1,6\]
**Explantion:** To make one jumbo burger and 6 small burgers we need 4\*1 + 2\*6 = 16 tomato and 1 + 6 = 7 cheese.
There will be no remaining ingredients.
**Example 2:**
**Input:** tomatoSlices = 17, cheeseSlices = 4
**Output:** \[\]
**Explantion:** There will be no way to use all ingredients to make small and jumbo burgers.
**Example 3:**
**Input:** tomatoSlices = 4, cheeseSlices = 17
**Output:** \[\]
**Explantion:** Making 1 jumbo burger there will be 16 cheese remaining and making 2 small burgers there will be 15 cheese remaining.
**Constraints:**
* `0 <= tomatoSlices, cheeseSlices <= 107` | Find the divisors of n+1 and n+2. To find the divisors of a number, you only need to iterate to the square root of that number. |
Python 3 Solution | closest-divisors | 0 | 1 | # Code\n```\nclass Solution:\n def closestDivisors(self, num: int) -> List[int]:\n\n for x in range(isqrt(num)+1,1,-1):\n if (num+1)%x == 0:\n return [(num + 1)//x,x]\n\n if (num+2)%x == 0:\n return [(num + 2)//x,x]\n\n \n``` | 0 | Given an integer `num`, find the closest two integers in absolute difference whose product equals `num + 1` or `num + 2`.
Return the two integers in any order.
**Example 1:**
**Input:** num = 8
**Output:** \[3,3\]
**Explanation:** For num + 1 = 9, the closest divisors are 3 & 3, for num + 2 = 10, the closest divisors are 2 & 5, hence 3 & 3 is chosen.
**Example 2:**
**Input:** num = 123
**Output:** \[5,25\]
**Example 3:**
**Input:** num = 999
**Output:** \[40,25\]
**Constraints:**
* `1 <= num <= 10^9` | Let f(n) denote the probability of the n-th person getting correct seat in n-person case, then:
f(1) = 1 (base case, trivial)
f(2) = 1/2 (also trivial) Try to calculate f(3), f(4), and f(5) using the base cases. What if the value of them?
f(i) for i >= 2 will also be 1/2. Try to proof why f(i) = 1/2 for i >= 2. |
Python 3 Solution | closest-divisors | 0 | 1 | # Code\n```\nclass Solution:\n def closestDivisors(self, num: int) -> List[int]:\n\n for x in range(isqrt(num)+1,1,-1):\n if (num+1)%x == 0:\n return [(num + 1)//x,x]\n\n if (num+2)%x == 0:\n return [(num + 2)//x,x]\n\n \n``` | 0 | Given two integers `tomatoSlices` and `cheeseSlices`. The ingredients of different burgers are as follows:
* **Jumbo Burger:** `4` tomato slices and `1` cheese slice.
* **Small Burger:** `2` Tomato slices and `1` cheese slice.
Return `[total_jumbo, total_small]` so that the number of remaining `tomatoSlices` equal to `0` and the number of remaining `cheeseSlices` equal to `0`. If it is not possible to make the remaining `tomatoSlices` and `cheeseSlices` equal to `0` return `[]`.
**Example 1:**
**Input:** tomatoSlices = 16, cheeseSlices = 7
**Output:** \[1,6\]
**Explantion:** To make one jumbo burger and 6 small burgers we need 4\*1 + 2\*6 = 16 tomato and 1 + 6 = 7 cheese.
There will be no remaining ingredients.
**Example 2:**
**Input:** tomatoSlices = 17, cheeseSlices = 4
**Output:** \[\]
**Explantion:** There will be no way to use all ingredients to make small and jumbo burgers.
**Example 3:**
**Input:** tomatoSlices = 4, cheeseSlices = 17
**Output:** \[\]
**Explantion:** Making 1 jumbo burger there will be 16 cheese remaining and making 2 small burgers there will be 15 cheese remaining.
**Constraints:**
* `0 <= tomatoSlices, cheeseSlices <= 107` | Find the divisors of n+1 and n+2. To find the divisors of a number, you only need to iterate to the square root of that number. |
Python; 100% faster || T: O(n) S: O(1) || Dictionary + Math || | largest-multiple-of-three | 0 | 1 | # Intuition\nMaximize the answer my choosing current available max number.\n\nAfter all numbers exhausted delete some numbers for correcting remainder.\n# Approach\nFirst find max number using counter dictionary. \n\nthen adjust it to multiple of 3 by\n\nNOTE :(For those who did not understood del2 call from del1): \nMathematically if in case remainder is 1 it could be of two reasons \n- due to a ones(1,4,7) element.\n- due to twos(2,5,8) element occuring twice.\n\n# Complexity\n- Time complexity:\nO(n) \n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def del1(self,ans):\n i=len(ans)-1\n ones={"1","4","7"}\n while i>-1 and ans[i] not in ones:i-=1\n if i==-1:return self.del2(self.del2(ans))\n return ans[:i]+ans[i+1:]\n\n def del2(self,ans):\n i=len(ans)-1\n twos={"2","5","8"}\n while i>-1 and ans[i] not in twos:i-=1\n if i==-1:return self.del1(self.del1(ans))\n return ans[:i]+ans[i+1:]\n \n\n def largestMultipleOfThree(self, digits: List[int]) -> str:\n c=Counter(digits)\n ans,rem="",0\n for i in range(9,0,-1):\n ans+=str(i)*c[i]\n rem=(rem+i*c[i]%3)%3\n \n if rem==1:ans=self.del1(ans)\n if rem==2:ans=self.del2(ans)\n return ans+"0"*c[0] if ans else "0" if 0 in c else ""\n\n \n \n``` | 2 | Given an array of digits `digits`, return _the largest multiple of **three** that can be formed by concatenating some of the given digits in **any order**_. If there is no answer return an empty string.
Since the answer may not fit in an integer data type, return the answer as a string. Note that the returning answer must not contain unnecessary leading zeros.
**Example 1:**
**Input:** digits = \[8,1,9\]
**Output:** "981 "
**Example 2:**
**Input:** digits = \[8,6,7,1,0\]
**Output:** "8760 "
**Example 3:**
**Input:** digits = \[1\]
**Output:** " "
**Constraints:**
* `1 <= digits.length <= 104`
* `0 <= digits[i] <= 9` | null |
Python; 100% faster || T: O(n) S: O(1) || Dictionary + Math || | largest-multiple-of-three | 0 | 1 | # Intuition\nMaximize the answer my choosing current available max number.\n\nAfter all numbers exhausted delete some numbers for correcting remainder.\n# Approach\nFirst find max number using counter dictionary. \n\nthen adjust it to multiple of 3 by\n\nNOTE :(For those who did not understood del2 call from del1): \nMathematically if in case remainder is 1 it could be of two reasons \n- due to a ones(1,4,7) element.\n- due to twos(2,5,8) element occuring twice.\n\n# Complexity\n- Time complexity:\nO(n) \n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def del1(self,ans):\n i=len(ans)-1\n ones={"1","4","7"}\n while i>-1 and ans[i] not in ones:i-=1\n if i==-1:return self.del2(self.del2(ans))\n return ans[:i]+ans[i+1:]\n\n def del2(self,ans):\n i=len(ans)-1\n twos={"2","5","8"}\n while i>-1 and ans[i] not in twos:i-=1\n if i==-1:return self.del1(self.del1(ans))\n return ans[:i]+ans[i+1:]\n \n\n def largestMultipleOfThree(self, digits: List[int]) -> str:\n c=Counter(digits)\n ans,rem="",0\n for i in range(9,0,-1):\n ans+=str(i)*c[i]\n rem=(rem+i*c[i]%3)%3\n \n if rem==1:ans=self.del1(ans)\n if rem==2:ans=self.del2(ans)\n return ans+"0"*c[0] if ans else "0" if 0 in c else ""\n\n \n \n``` | 2 | Given a `m * n` matrix of ones and zeros, return how many **square** submatrices have all ones.
**Example 1:**
**Input:** matrix =
\[
\[0,1,1,1\],
\[1,1,1,1\],
\[0,1,1,1\]
\]
**Output:** 15
**Explanation:**
There are **10** squares of side 1.
There are **4** squares of side 2.
There is **1** square of side 3.
Total number of squares = 10 + 4 + 1 = **15**.
**Example 2:**
**Input:** matrix =
\[
\[1,0,1\],
\[1,1,0\],
\[1,1,0\]
\]
**Output:** 7
**Explanation:**
There are **6** squares of side 1.
There is **1** square of side 2.
Total number of squares = 6 + 1 = **7**.
**Constraints:**
* `1 <= arr.length <= 300`
* `1 <= arr[0].length <= 300`
* `0 <= arr[i][j] <= 1` | A number is a multiple of three if and only if its sum of digits is a multiple of three. Use dynamic programming. To find the maximum number, try to maximize the number of digits of the number. Sort the digits in descending order to find the maximum number. |
[Python] O(n) Simple Bucket Sort with Explanation | largest-multiple-of-three | 0 | 1 | **Idea**\nAccording to the **3 divisibility rule** (proof: https://math.stackexchange.com/questions/341202/how-to-prove-the-divisibility-rule-for-3-casting-out-threes).\nOur goal is to find **the maximum number of digits whose sum is a multiple of 3**.\n\nWe categorize all the input digits into 3 category. \n- `{0, 3, 9}`: these digits should be accepted into our candidates no matter what\n- `{1, 4, 7}`: **category 1**, these digits can only be accepted into out candidates **3 in a group**, or together with 1 element from **category 2**\n- `{2, 5, 8}`: **category 2**, these digits can only be accepted into out candidates **3 in a group**, or together with 1 element from **category 1**\n\nEdge case: `[1,1,1,2,2]` and `[1,1,1,2]`. We need to distinguish these 2 edge cases.\n- in cases like `[1,1,1,2]`\n - we need to take from **category 1** and **category 2** 3 elements in a group first\n- in cases like `[1,1,1,2,2]`\n - we need to take 1 element from both **category 1** and **category 2** first\n\n**Complexity**\nTIme: `O(n)` using bucket sort\nSpace: `O(n)`\n\n**Python 3, Bucket Sort, O(n) in time and space, more readable but longer**\n```\nclass Solution:\n def largestMultipleOfThree(self, digits: List[int]) -> str:\n def bucket_sorted(arr):\n c = collections.Counter(arr)\n return [x for i in range(10) if i in c for x in [i]*c[i]]\n \n d = collections.defaultdict(list)\n for n in digits:\n d[n%3] += n,\n res, short, long = d[0], *sorted((d[1], d[2]), key=len)\n short, long = bucket_sorted(short), bucket_sorted(long)\n \n if (len(long) - len(short)) % 3 > abs((len(long) % 3) - (len(short) % 3)):\n short, long = (short, long) if len(short)%3 < len(long)%3 else (long, short)\n res += short + long[abs(len(short)%3 - len(long)%3):]\n else:\n res += short + long[(len(long)-len(short))%3:]\n \n res = bucket_sorted(res)[::-1]\n return \'0\' if res and not res[0] else \'\'.join(map(str, res))\n```\n\n**Python 3, using reduce and default sort, O(nlogn)**\n```\nfrom functools import reduce\nclass Solution:\n def largestMultipleOfThree(self, digits: List[int]) -> str: \n d, _ = reduce(lambda pair,y:(pair[0],pair[0][y%3].append(y)), digits, (collections.defaultdict(list), None))\n res, short, long = d[0], *sorted([sorted(arr) for arr in (d[1], d[2])], key=len)\n \n if (len(long) - len(short)) % 3 > abs((len(long) % 3) - (len(short) % 3)):\n short, long = (short, long) if len(short)%3 < len(long)%3 else (long, short)\n res += short + long[abs(len(short)%3 - len(long)%3):]\n else:\n res += short + long[(len(long)-len(short))%3:]\n \n res = res.sort(reverse=True)\n return \'0\' if res and not res[0] else \'\'.join(map(str, res))\n``` | 12 | Given an array of digits `digits`, return _the largest multiple of **three** that can be formed by concatenating some of the given digits in **any order**_. If there is no answer return an empty string.
Since the answer may not fit in an integer data type, return the answer as a string. Note that the returning answer must not contain unnecessary leading zeros.
**Example 1:**
**Input:** digits = \[8,1,9\]
**Output:** "981 "
**Example 2:**
**Input:** digits = \[8,6,7,1,0\]
**Output:** "8760 "
**Example 3:**
**Input:** digits = \[1\]
**Output:** " "
**Constraints:**
* `1 <= digits.length <= 104`
* `0 <= digits[i] <= 9` | null |
[Python] O(n) Simple Bucket Sort with Explanation | largest-multiple-of-three | 0 | 1 | **Idea**\nAccording to the **3 divisibility rule** (proof: https://math.stackexchange.com/questions/341202/how-to-prove-the-divisibility-rule-for-3-casting-out-threes).\nOur goal is to find **the maximum number of digits whose sum is a multiple of 3**.\n\nWe categorize all the input digits into 3 category. \n- `{0, 3, 9}`: these digits should be accepted into our candidates no matter what\n- `{1, 4, 7}`: **category 1**, these digits can only be accepted into out candidates **3 in a group**, or together with 1 element from **category 2**\n- `{2, 5, 8}`: **category 2**, these digits can only be accepted into out candidates **3 in a group**, or together with 1 element from **category 1**\n\nEdge case: `[1,1,1,2,2]` and `[1,1,1,2]`. We need to distinguish these 2 edge cases.\n- in cases like `[1,1,1,2]`\n - we need to take from **category 1** and **category 2** 3 elements in a group first\n- in cases like `[1,1,1,2,2]`\n - we need to take 1 element from both **category 1** and **category 2** first\n\n**Complexity**\nTIme: `O(n)` using bucket sort\nSpace: `O(n)`\n\n**Python 3, Bucket Sort, O(n) in time and space, more readable but longer**\n```\nclass Solution:\n def largestMultipleOfThree(self, digits: List[int]) -> str:\n def bucket_sorted(arr):\n c = collections.Counter(arr)\n return [x for i in range(10) if i in c for x in [i]*c[i]]\n \n d = collections.defaultdict(list)\n for n in digits:\n d[n%3] += n,\n res, short, long = d[0], *sorted((d[1], d[2]), key=len)\n short, long = bucket_sorted(short), bucket_sorted(long)\n \n if (len(long) - len(short)) % 3 > abs((len(long) % 3) - (len(short) % 3)):\n short, long = (short, long) if len(short)%3 < len(long)%3 else (long, short)\n res += short + long[abs(len(short)%3 - len(long)%3):]\n else:\n res += short + long[(len(long)-len(short))%3:]\n \n res = bucket_sorted(res)[::-1]\n return \'0\' if res and not res[0] else \'\'.join(map(str, res))\n```\n\n**Python 3, using reduce and default sort, O(nlogn)**\n```\nfrom functools import reduce\nclass Solution:\n def largestMultipleOfThree(self, digits: List[int]) -> str: \n d, _ = reduce(lambda pair,y:(pair[0],pair[0][y%3].append(y)), digits, (collections.defaultdict(list), None))\n res, short, long = d[0], *sorted([sorted(arr) for arr in (d[1], d[2])], key=len)\n \n if (len(long) - len(short)) % 3 > abs((len(long) % 3) - (len(short) % 3)):\n short, long = (short, long) if len(short)%3 < len(long)%3 else (long, short)\n res += short + long[abs(len(short)%3 - len(long)%3):]\n else:\n res += short + long[(len(long)-len(short))%3:]\n \n res = res.sort(reverse=True)\n return \'0\' if res and not res[0] else \'\'.join(map(str, res))\n``` | 12 | Given a `m * n` matrix of ones and zeros, return how many **square** submatrices have all ones.
**Example 1:**
**Input:** matrix =
\[
\[0,1,1,1\],
\[1,1,1,1\],
\[0,1,1,1\]
\]
**Output:** 15
**Explanation:**
There are **10** squares of side 1.
There are **4** squares of side 2.
There is **1** square of side 3.
Total number of squares = 10 + 4 + 1 = **15**.
**Example 2:**
**Input:** matrix =
\[
\[1,0,1\],
\[1,1,0\],
\[1,1,0\]
\]
**Output:** 7
**Explanation:**
There are **6** squares of side 1.
There is **1** square of side 2.
Total number of squares = 6 + 1 = **7**.
**Constraints:**
* `1 <= arr.length <= 300`
* `1 <= arr[0].length <= 300`
* `0 <= arr[i][j] <= 1` | A number is a multiple of three if and only if its sum of digits is a multiple of three. Use dynamic programming. To find the maximum number, try to maximize the number of digits of the number. Sort the digits in descending order to find the maximum number. |
Whatever Jutsu Solution | largest-multiple-of-three | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n```\nclass Solution:\n def largestMultipleOfThree(self, digits: List[int]) -> str:\n s = sum(digits)\n digits.sort(reverse=True)\n d = defaultdict(int)\n x = -1\n y = -1\n if s%3!=0:\n for i in range(len(digits)-1,-1,-1):\n s -= digits[i]\n if digits[i]%3!=0:\n d[digits[i]]+=1\n if s%3==0:\n x = i\n break\n s += digits[i]\n if s%3!=0 and x==-1:\n f = False\n temp = float(\'inf\')\n for i in d:\n for j in d:\n print(i,j,s-i-j)\n if i == j:\n if (s-2*j)%3==0 and d[i]>1 and i+j<temp:\n x = i\n y = j\n temp = i+j\n else:\n if (s-j-i)%3==0 and i+j<temp:\n x = i\n y = j\n temp = i+j\n res = ""\n for i in range(len(digits)):\n if digits[i] == x:\n x = -1\n continue\n elif digits[i] == y:\n y = -1\n continue\n res += str(digits[i])\n if res and res[0] == "0":\n return "0"\n return res\n res = ""\n for i in range(len(digits)):\n if i == x:\n continue\n res += str(digits[i])\n if res and res[0] == "0":\n return \'0\'\n return res\n``` | 0 | Given an array of digits `digits`, return _the largest multiple of **three** that can be formed by concatenating some of the given digits in **any order**_. If there is no answer return an empty string.
Since the answer may not fit in an integer data type, return the answer as a string. Note that the returning answer must not contain unnecessary leading zeros.
**Example 1:**
**Input:** digits = \[8,1,9\]
**Output:** "981 "
**Example 2:**
**Input:** digits = \[8,6,7,1,0\]
**Output:** "8760 "
**Example 3:**
**Input:** digits = \[1\]
**Output:** " "
**Constraints:**
* `1 <= digits.length <= 104`
* `0 <= digits[i] <= 9` | null |
Whatever Jutsu Solution | largest-multiple-of-three | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n```\nclass Solution:\n def largestMultipleOfThree(self, digits: List[int]) -> str:\n s = sum(digits)\n digits.sort(reverse=True)\n d = defaultdict(int)\n x = -1\n y = -1\n if s%3!=0:\n for i in range(len(digits)-1,-1,-1):\n s -= digits[i]\n if digits[i]%3!=0:\n d[digits[i]]+=1\n if s%3==0:\n x = i\n break\n s += digits[i]\n if s%3!=0 and x==-1:\n f = False\n temp = float(\'inf\')\n for i in d:\n for j in d:\n print(i,j,s-i-j)\n if i == j:\n if (s-2*j)%3==0 and d[i]>1 and i+j<temp:\n x = i\n y = j\n temp = i+j\n else:\n if (s-j-i)%3==0 and i+j<temp:\n x = i\n y = j\n temp = i+j\n res = ""\n for i in range(len(digits)):\n if digits[i] == x:\n x = -1\n continue\n elif digits[i] == y:\n y = -1\n continue\n res += str(digits[i])\n if res and res[0] == "0":\n return "0"\n return res\n res = ""\n for i in range(len(digits)):\n if i == x:\n continue\n res += str(digits[i])\n if res and res[0] == "0":\n return \'0\'\n return res\n``` | 0 | Given a `m * n` matrix of ones and zeros, return how many **square** submatrices have all ones.
**Example 1:**
**Input:** matrix =
\[
\[0,1,1,1\],
\[1,1,1,1\],
\[0,1,1,1\]
\]
**Output:** 15
**Explanation:**
There are **10** squares of side 1.
There are **4** squares of side 2.
There is **1** square of side 3.
Total number of squares = 10 + 4 + 1 = **15**.
**Example 2:**
**Input:** matrix =
\[
\[1,0,1\],
\[1,1,0\],
\[1,1,0\]
\]
**Output:** 7
**Explanation:**
There are **6** squares of side 1.
There is **1** square of side 2.
Total number of squares = 6 + 1 = **7**.
**Constraints:**
* `1 <= arr.length <= 300`
* `1 <= arr[0].length <= 300`
* `0 <= arr[i][j] <= 1` | A number is a multiple of three if and only if its sum of digits is a multiple of three. Use dynamic programming. To find the maximum number, try to maximize the number of digits of the number. Sort the digits in descending order to find the maximum number. |
Over*simplification eFINALITYpi: | largest-multiple-of-three | 0 | 1 | ```\nclass Solution:\n def largestMultipleOfThree(self, d: List[int]) -> str:\n for i in [c:=Counter(d),o:=sum(d)%3,1,2][2:]*(0<o):\n if o and len(z:=list(islice(chain(*([e]*min(c[e],i) for e in range(i*o%3,9,3))),i)))==i:\n for e in z:c[e]-=1;o=0\n return \'\' if o else \'0\' if (m:=\'\'.join(str(9-e)*c[9-e]for e in range(10)))[:1]==\'0\' else m\n```\n\n\n | 0 | Given an array of digits `digits`, return _the largest multiple of **three** that can be formed by concatenating some of the given digits in **any order**_. If there is no answer return an empty string.
Since the answer may not fit in an integer data type, return the answer as a string. Note that the returning answer must not contain unnecessary leading zeros.
**Example 1:**
**Input:** digits = \[8,1,9\]
**Output:** "981 "
**Example 2:**
**Input:** digits = \[8,6,7,1,0\]
**Output:** "8760 "
**Example 3:**
**Input:** digits = \[1\]
**Output:** " "
**Constraints:**
* `1 <= digits.length <= 104`
* `0 <= digits[i] <= 9` | null |
Over*simplification eFINALITYpi: | largest-multiple-of-three | 0 | 1 | ```\nclass Solution:\n def largestMultipleOfThree(self, d: List[int]) -> str:\n for i in [c:=Counter(d),o:=sum(d)%3,1,2][2:]*(0<o):\n if o and len(z:=list(islice(chain(*([e]*min(c[e],i) for e in range(i*o%3,9,3))),i)))==i:\n for e in z:c[e]-=1;o=0\n return \'\' if o else \'0\' if (m:=\'\'.join(str(9-e)*c[9-e]for e in range(10)))[:1]==\'0\' else m\n```\n\n\n | 0 | Given a `m * n` matrix of ones and zeros, return how many **square** submatrices have all ones.
**Example 1:**
**Input:** matrix =
\[
\[0,1,1,1\],
\[1,1,1,1\],
\[0,1,1,1\]
\]
**Output:** 15
**Explanation:**
There are **10** squares of side 1.
There are **4** squares of side 2.
There is **1** square of side 3.
Total number of squares = 10 + 4 + 1 = **15**.
**Example 2:**
**Input:** matrix =
\[
\[1,0,1\],
\[1,1,0\],
\[1,1,0\]
\]
**Output:** 7
**Explanation:**
There are **6** squares of side 1.
There is **1** square of side 2.
Total number of squares = 6 + 1 = **7**.
**Constraints:**
* `1 <= arr.length <= 300`
* `1 <= arr[0].length <= 300`
* `0 <= arr[i][j] <= 1` | A number is a multiple of three if and only if its sum of digits is a multiple of three. Use dynamic programming. To find the maximum number, try to maximize the number of digits of the number. Sort the digits in descending order to find the maximum number. |
Python3||DP | largest-multiple-of-three | 0 | 1 | # Intuition\n- Intituion is that find the largest sum in the array divisble by three and try to trace it\n\n# Approach\n- DP\n\n# Complexity\n- Time complexity:\n- O(N^2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestMultipleOfThree(self, digits: List[int]) -> str:\n # checking if s is greater than s1\n def checkGreater(s,s1):\n if len(s) > len(s1):\n return True\n elif len(s1) > len(s):\n return False\n elif s1 == s:\n return True\n else:\n for i in range(len(s)):\n d = int(s[i])\n d1 = int(s1[i])\n if d > d1:\n return True\n elif d1>d:\n return False\n return True\n\n def solve(digits):\n # sorting digits\n digits.sort()\n digits = digits[-1::-1]\n # dp array\n dp = [[("",0) for _ in range(3)] for _ in range(len(digits)+1)]\n\n for i in range(1,len(digits)+1):\n num = digits[i-1]\n\n #copying values downward\n for j in range(3):\n dp[i][j] = dp[i-1][j]\n\n for j in range(3):\n summ = dp[i-1][j][1]+num\n res = dp[i-1][j][0]+str(num)\n if dp[i][summ%3][0] != \'\':\n if checkGreater(res,dp[i][summ%3][0]):\n dp[i][summ%3] = (res,summ)\n else:\n dp[i][summ%3] = (res,summ)\n\n res = ""\n val = dp[len(digits)][0][0]\n for i in range(len(val)):\n if val[i] == \'0\' and len(res) == 0:\n continue\n else:\n res+=val[i]\n if res!="":\n return res\n elif 0 in digits:\n return "0"\n else:\n return \'\'\n return solve(digits)\n\n\n\n``` | 0 | Given an array of digits `digits`, return _the largest multiple of **three** that can be formed by concatenating some of the given digits in **any order**_. If there is no answer return an empty string.
Since the answer may not fit in an integer data type, return the answer as a string. Note that the returning answer must not contain unnecessary leading zeros.
**Example 1:**
**Input:** digits = \[8,1,9\]
**Output:** "981 "
**Example 2:**
**Input:** digits = \[8,6,7,1,0\]
**Output:** "8760 "
**Example 3:**
**Input:** digits = \[1\]
**Output:** " "
**Constraints:**
* `1 <= digits.length <= 104`
* `0 <= digits[i] <= 9` | null |
Python3||DP | largest-multiple-of-three | 0 | 1 | # Intuition\n- Intituion is that find the largest sum in the array divisble by three and try to trace it\n\n# Approach\n- DP\n\n# Complexity\n- Time complexity:\n- O(N^2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestMultipleOfThree(self, digits: List[int]) -> str:\n # checking if s is greater than s1\n def checkGreater(s,s1):\n if len(s) > len(s1):\n return True\n elif len(s1) > len(s):\n return False\n elif s1 == s:\n return True\n else:\n for i in range(len(s)):\n d = int(s[i])\n d1 = int(s1[i])\n if d > d1:\n return True\n elif d1>d:\n return False\n return True\n\n def solve(digits):\n # sorting digits\n digits.sort()\n digits = digits[-1::-1]\n # dp array\n dp = [[("",0) for _ in range(3)] for _ in range(len(digits)+1)]\n\n for i in range(1,len(digits)+1):\n num = digits[i-1]\n\n #copying values downward\n for j in range(3):\n dp[i][j] = dp[i-1][j]\n\n for j in range(3):\n summ = dp[i-1][j][1]+num\n res = dp[i-1][j][0]+str(num)\n if dp[i][summ%3][0] != \'\':\n if checkGreater(res,dp[i][summ%3][0]):\n dp[i][summ%3] = (res,summ)\n else:\n dp[i][summ%3] = (res,summ)\n\n res = ""\n val = dp[len(digits)][0][0]\n for i in range(len(val)):\n if val[i] == \'0\' and len(res) == 0:\n continue\n else:\n res+=val[i]\n if res!="":\n return res\n elif 0 in digits:\n return "0"\n else:\n return \'\'\n return solve(digits)\n\n\n\n``` | 0 | Given a `m * n` matrix of ones and zeros, return how many **square** submatrices have all ones.
**Example 1:**
**Input:** matrix =
\[
\[0,1,1,1\],
\[1,1,1,1\],
\[0,1,1,1\]
\]
**Output:** 15
**Explanation:**
There are **10** squares of side 1.
There are **4** squares of side 2.
There is **1** square of side 3.
Total number of squares = 10 + 4 + 1 = **15**.
**Example 2:**
**Input:** matrix =
\[
\[1,0,1\],
\[1,1,0\],
\[1,1,0\]
\]
**Output:** 7
**Explanation:**
There are **6** squares of side 1.
There is **1** square of side 2.
Total number of squares = 6 + 1 = **7**.
**Constraints:**
* `1 <= arr.length <= 300`
* `1 <= arr[0].length <= 300`
* `0 <= arr[i][j] <= 1` | A number is a multiple of three if and only if its sum of digits is a multiple of three. Use dynamic programming. To find the maximum number, try to maximize the number of digits of the number. Sort the digits in descending order to find the maximum number. |
Python: Got past TLE with hack | largest-multiple-of-three | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAt first, I tried the approach suggested by the Hint: Use dynamic\nprogramming to find the solution. However, even using ```lru_cache(None)``` to accelerate the DP, I was still getting Time Limit Exceeded. I then came up with a hack that can significantly speed up some cases; I left the DP in place to handle other cases.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI will focus on the two hacks and skip discussing the DP part, since that follows a typical DP pattern (base case, recursion cases).\n\nThe hack is based on the observation that, for a given set of digits, there are only three possible sums modulo 3: 0, 1, and 2. If we look at the original list of digits and its modular residue, if it\'s 0, we don\'t need to look for the longest sum-mod-3 subsequence: just take all the digits (sorting them descending). What if the residue is 1? Well, if we can find a 1 *somewhere* in the digits, we can simply remove it adjusting the residue down to 0 (we can also do this with 4\'s or 7\'s, but I didn\'t bother), and use all the rest of the digits. Similarly, if the residue is 2 and we can find one "2" (or 5 or 8) and remove it, we reduce the residue to 0 and can use all the rest of the digits.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe overall time complexity for the DP would be $$O(2^n)$$ or less if we use memo-ization. We know the time complexity is at least $$O(n)$$, since we have to look at every digit; when the hack above applies (which is often the case for large examples) that becomes the overall time complexity.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe only significant data structure (not counting the execution stack) is the ```lru_cache```. I found that setting the cache size to None (unlimited) I ran out of storage on the larger examples, and reducing it to 100,000 fixed the storage problem but still gave a TLE.\n# Code\n```\nclass Solution:\n def largestMultipleOfThree(self, digits: list[int]) -> str:\n # Sort the digits in descending order; this will make any resulting subsequence\n # also be in sorted order, which gives the largest number from the set of digits\n self.digits = sorted( digits, key = lambda digit: - digit )\n digits_sum = sum( self.digits )\n print( "digits_sum % 3", digits_sum % 3 )\n residue = digits_sum % 3\n if residue == 0:\n return self.postProcess( self.digits )\n elif residue == 1:\n if self.digits.count( 1 ):\n index_1 = self.digits.index( 1 )\n self.digits.pop( index_1 )\n return self.postProcess( self.digits )\n elif residue == 2:\n if self.digits.count( 2 ):\n index_2 = self.digits.index( 2 )\n print( "self.digits before pop", self.digits, "index_2", index_2 )\n self.digits.pop( index_2 )\n print( "self.digits after pop for 2", self.digits )\n return self.postProcess( self.digits ) \n # As the hint suggests, the first step is to find a multiple of three\n # that has the greatest number of digits:\n print( "digits has", digits.count( 1 ), "1\'s and", digits.count( 2 ), "2\'s")\n index = 0\n sum_so_far = 0\n mostDigits = self.findMostDigits(index, sum_so_far);\n return self.postProcess( mostDigits ) \n\n @lru_cache( 100_000 )\n def findMostDigits(self, index, sum_so_far):\n # Base case:\n if index == len(self.digits):\n result = [] if sum_so_far % 3 == 0 else None\n # Recursion case:\n else:\n # Try adding "digits[index]" to result\n rec_res_with = self.findMostDigits(index + 1, sum_so_far + self.digits[index])\n if rec_res_with is not None:\n result = [self.digits[index]] + rec_res_with\n else:\n result = None\n # Try NOT adding "digits[index]" to result\n rec_res_without = self.findMostDigits(index + 1, sum_so_far)\n if rec_res_without is not None:\n if result is not None:\n result = rec_res_without if len( rec_res_without ) > len( result ) else result\n else:\n result = rec_res_without\n return result\n\n # This converts "digits" to a string and handles the case where there are leading zeros and\n # the case where there are no digits\n def postProcess( self, digits ):\n print( "digits", digits )\n if digits is None or len( digits ) == 0:\n return ""\n elif sum( digits ) == 0:\n return "0"\n else:\n return \'\'.join( map( str, digits ) )\n``` | 0 | Given an array of digits `digits`, return _the largest multiple of **three** that can be formed by concatenating some of the given digits in **any order**_. If there is no answer return an empty string.
Since the answer may not fit in an integer data type, return the answer as a string. Note that the returning answer must not contain unnecessary leading zeros.
**Example 1:**
**Input:** digits = \[8,1,9\]
**Output:** "981 "
**Example 2:**
**Input:** digits = \[8,6,7,1,0\]
**Output:** "8760 "
**Example 3:**
**Input:** digits = \[1\]
**Output:** " "
**Constraints:**
* `1 <= digits.length <= 104`
* `0 <= digits[i] <= 9` | null |
Python: Got past TLE with hack | largest-multiple-of-three | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAt first, I tried the approach suggested by the Hint: Use dynamic\nprogramming to find the solution. However, even using ```lru_cache(None)``` to accelerate the DP, I was still getting Time Limit Exceeded. I then came up with a hack that can significantly speed up some cases; I left the DP in place to handle other cases.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI will focus on the two hacks and skip discussing the DP part, since that follows a typical DP pattern (base case, recursion cases).\n\nThe hack is based on the observation that, for a given set of digits, there are only three possible sums modulo 3: 0, 1, and 2. If we look at the original list of digits and its modular residue, if it\'s 0, we don\'t need to look for the longest sum-mod-3 subsequence: just take all the digits (sorting them descending). What if the residue is 1? Well, if we can find a 1 *somewhere* in the digits, we can simply remove it adjusting the residue down to 0 (we can also do this with 4\'s or 7\'s, but I didn\'t bother), and use all the rest of the digits. Similarly, if the residue is 2 and we can find one "2" (or 5 or 8) and remove it, we reduce the residue to 0 and can use all the rest of the digits.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe overall time complexity for the DP would be $$O(2^n)$$ or less if we use memo-ization. We know the time complexity is at least $$O(n)$$, since we have to look at every digit; when the hack above applies (which is often the case for large examples) that becomes the overall time complexity.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe only significant data structure (not counting the execution stack) is the ```lru_cache```. I found that setting the cache size to None (unlimited) I ran out of storage on the larger examples, and reducing it to 100,000 fixed the storage problem but still gave a TLE.\n# Code\n```\nclass Solution:\n def largestMultipleOfThree(self, digits: list[int]) -> str:\n # Sort the digits in descending order; this will make any resulting subsequence\n # also be in sorted order, which gives the largest number from the set of digits\n self.digits = sorted( digits, key = lambda digit: - digit )\n digits_sum = sum( self.digits )\n print( "digits_sum % 3", digits_sum % 3 )\n residue = digits_sum % 3\n if residue == 0:\n return self.postProcess( self.digits )\n elif residue == 1:\n if self.digits.count( 1 ):\n index_1 = self.digits.index( 1 )\n self.digits.pop( index_1 )\n return self.postProcess( self.digits )\n elif residue == 2:\n if self.digits.count( 2 ):\n index_2 = self.digits.index( 2 )\n print( "self.digits before pop", self.digits, "index_2", index_2 )\n self.digits.pop( index_2 )\n print( "self.digits after pop for 2", self.digits )\n return self.postProcess( self.digits ) \n # As the hint suggests, the first step is to find a multiple of three\n # that has the greatest number of digits:\n print( "digits has", digits.count( 1 ), "1\'s and", digits.count( 2 ), "2\'s")\n index = 0\n sum_so_far = 0\n mostDigits = self.findMostDigits(index, sum_so_far);\n return self.postProcess( mostDigits ) \n\n @lru_cache( 100_000 )\n def findMostDigits(self, index, sum_so_far):\n # Base case:\n if index == len(self.digits):\n result = [] if sum_so_far % 3 == 0 else None\n # Recursion case:\n else:\n # Try adding "digits[index]" to result\n rec_res_with = self.findMostDigits(index + 1, sum_so_far + self.digits[index])\n if rec_res_with is not None:\n result = [self.digits[index]] + rec_res_with\n else:\n result = None\n # Try NOT adding "digits[index]" to result\n rec_res_without = self.findMostDigits(index + 1, sum_so_far)\n if rec_res_without is not None:\n if result is not None:\n result = rec_res_without if len( rec_res_without ) > len( result ) else result\n else:\n result = rec_res_without\n return result\n\n # This converts "digits" to a string and handles the case where there are leading zeros and\n # the case where there are no digits\n def postProcess( self, digits ):\n print( "digits", digits )\n if digits is None or len( digits ) == 0:\n return ""\n elif sum( digits ) == 0:\n return "0"\n else:\n return \'\'.join( map( str, digits ) )\n``` | 0 | Given a `m * n` matrix of ones and zeros, return how many **square** submatrices have all ones.
**Example 1:**
**Input:** matrix =
\[
\[0,1,1,1\],
\[1,1,1,1\],
\[0,1,1,1\]
\]
**Output:** 15
**Explanation:**
There are **10** squares of side 1.
There are **4** squares of side 2.
There is **1** square of side 3.
Total number of squares = 10 + 4 + 1 = **15**.
**Example 2:**
**Input:** matrix =
\[
\[1,0,1\],
\[1,1,0\],
\[1,1,0\]
\]
**Output:** 7
**Explanation:**
There are **6** squares of side 1.
There is **1** square of side 2.
Total number of squares = 6 + 1 = **7**.
**Constraints:**
* `1 <= arr.length <= 300`
* `1 <= arr[0].length <= 300`
* `0 <= arr[i][j] <= 1` | A number is a multiple of three if and only if its sum of digits is a multiple of three. Use dynamic programming. To find the maximum number, try to maximize the number of digits of the number. Sort the digits in descending order to find the maximum number. |
Solution | largest-multiple-of-three | 0 | 1 | To find the largest multiple of three, we need to consider the following cases:\n\n1. If the sum of all digits is divisible by 3, we can use all the digits to form the largest multiple of three. In this case, we should sort the digits in non-ascending order and return the result as a string.\n\n2. If the sum of all digits modulo 3 is 1, we need to remove one digit with a remainder of 1 (if available) or two digits with a remainder of 2 (if available) to make the sum divisible by 3. To maximize the resulting number, we should prioritize removing digits with larger values. Therefore, we can sort the digits in non-ascending order and try to remove the smallest digit(s) with the corresponding remainder(s). After removing the necessary digits, we should return the remaining digits as the result if any exist.\n3. If the sum of all digits modulo 3 is 2, we need to remove one digit with a remainder of 2 (if available) or two digits with a remainder of 1 (if available) to make the sum divisible by 3. Similar to the previous case, we should sort the digits in non-ascending order and remove the smallest digit(s) with the corresponding remainder(s). Finally, we return the remaining digits as the result if any exist.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n```\nfrom typing import List\n\nclass Solution:\n def largestMultipleOfThree(self, digits: List[int]) -> str:\n digits.sort(reverse=True)\n total_sum = sum(digits)\n\n if total_sum % 3 == 0:\n if digits and digits[0] == 0:\n return "0"\n return \'\'.join(map(str, digits))\n\n remainder_1 = [digit for digit in digits if digit % 3 == 1]\n remainder_2 = [digit for digit in digits if digit % 3 == 2]\n\n if total_sum % 3 == 1:\n if remainder_1:\n digits.remove(remainder_1[-1])\n elif len(remainder_2) >= 2:\n digits.remove(remainder_2[-1])\n digits.remove(remainder_2[-2])\n else:\n return ""\n elif total_sum % 3 == 2:\n if remainder_2:\n digits.remove(remainder_2[-1])\n elif len(remainder_1) >= 2:\n digits.remove(remainder_1[-1])\n digits.remove(remainder_1[-2])\n else:\n return ""\n\n if digits and digits[0] == 0:\n return "0"\n return \'\'.join(map(str, digits))\n\n``` | 0 | Given an array of digits `digits`, return _the largest multiple of **three** that can be formed by concatenating some of the given digits in **any order**_. If there is no answer return an empty string.
Since the answer may not fit in an integer data type, return the answer as a string. Note that the returning answer must not contain unnecessary leading zeros.
**Example 1:**
**Input:** digits = \[8,1,9\]
**Output:** "981 "
**Example 2:**
**Input:** digits = \[8,6,7,1,0\]
**Output:** "8760 "
**Example 3:**
**Input:** digits = \[1\]
**Output:** " "
**Constraints:**
* `1 <= digits.length <= 104`
* `0 <= digits[i] <= 9` | null |
Solution | largest-multiple-of-three | 0 | 1 | To find the largest multiple of three, we need to consider the following cases:\n\n1. If the sum of all digits is divisible by 3, we can use all the digits to form the largest multiple of three. In this case, we should sort the digits in non-ascending order and return the result as a string.\n\n2. If the sum of all digits modulo 3 is 1, we need to remove one digit with a remainder of 1 (if available) or two digits with a remainder of 2 (if available) to make the sum divisible by 3. To maximize the resulting number, we should prioritize removing digits with larger values. Therefore, we can sort the digits in non-ascending order and try to remove the smallest digit(s) with the corresponding remainder(s). After removing the necessary digits, we should return the remaining digits as the result if any exist.\n3. If the sum of all digits modulo 3 is 2, we need to remove one digit with a remainder of 2 (if available) or two digits with a remainder of 1 (if available) to make the sum divisible by 3. Similar to the previous case, we should sort the digits in non-ascending order and remove the smallest digit(s) with the corresponding remainder(s). Finally, we return the remaining digits as the result if any exist.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n```\nfrom typing import List\n\nclass Solution:\n def largestMultipleOfThree(self, digits: List[int]) -> str:\n digits.sort(reverse=True)\n total_sum = sum(digits)\n\n if total_sum % 3 == 0:\n if digits and digits[0] == 0:\n return "0"\n return \'\'.join(map(str, digits))\n\n remainder_1 = [digit for digit in digits if digit % 3 == 1]\n remainder_2 = [digit for digit in digits if digit % 3 == 2]\n\n if total_sum % 3 == 1:\n if remainder_1:\n digits.remove(remainder_1[-1])\n elif len(remainder_2) >= 2:\n digits.remove(remainder_2[-1])\n digits.remove(remainder_2[-2])\n else:\n return ""\n elif total_sum % 3 == 2:\n if remainder_2:\n digits.remove(remainder_2[-1])\n elif len(remainder_1) >= 2:\n digits.remove(remainder_1[-1])\n digits.remove(remainder_1[-2])\n else:\n return ""\n\n if digits and digits[0] == 0:\n return "0"\n return \'\'.join(map(str, digits))\n\n``` | 0 | Given a `m * n` matrix of ones and zeros, return how many **square** submatrices have all ones.
**Example 1:**
**Input:** matrix =
\[
\[0,1,1,1\],
\[1,1,1,1\],
\[0,1,1,1\]
\]
**Output:** 15
**Explanation:**
There are **10** squares of side 1.
There are **4** squares of side 2.
There is **1** square of side 3.
Total number of squares = 10 + 4 + 1 = **15**.
**Example 2:**
**Input:** matrix =
\[
\[1,0,1\],
\[1,1,0\],
\[1,1,0\]
\]
**Output:** 7
**Explanation:**
There are **6** squares of side 1.
There is **1** square of side 2.
Total number of squares = 6 + 1 = **7**.
**Constraints:**
* `1 <= arr.length <= 300`
* `1 <= arr[0].length <= 300`
* `0 <= arr[i][j] <= 1` | A number is a multiple of three if and only if its sum of digits is a multiple of three. Use dynamic programming. To find the maximum number, try to maximize the number of digits of the number. Sort the digits in descending order to find the maximum number. |
Python solution faster than 99% with detailed explanation | largest-multiple-of-three | 0 | 1 | A number that is a multiple of three meets the property that the sum of all digits is a multiple of three. \nThus, we can try to find the answer from the three options from the n input digits in the following order: \n1. The answer is composed by all the n digits if the sum of all the n digits is a multiple of three.\n2. The answer is composed by n-1 digits by making the sum of n-1 digits a multiple of three. \n3. The answer is composed by n-2 digits by making the sum of n-2 digits a multiple of three. \n\nFor case 2 and case 3, the digit(s) to remove is the smaller the better. Finally, we can generate the answer by descending order of the available digits. \n\n```\nclass Solution:\n def find_one(self, digits, r):\n for i in range(r, 10, 3):\n if digits[i] > 0:\n digits[i] -= 1\n return True\n return False\n \n def find_two(self, digits, r):\n for i in range(3 - r, 10, 3):\n if digits[i] >= 2:\n digits[i] -= 2\n return True\n elif digits[i] == 1:\n for j in range(i + 3, 10, 3):\n if digits[j] >= 1:\n digits[i] -= 1\n digits[j] -= 1\n return True\n return False\n \n def largestMultipleOfThree(self, digits: List[int]) -> str:\n digits = Counter(digits)\n s = functools.reduce(lambda a, b: (a + b) % 3, [v * c % 3 for v, c in digits.items()])\n \n if s % 3 != 0 and not self.find_one(digits, s % 3) and not self.find_two(digits, s % 3):\n return ""\n ans = "".join(str(i)*digits[i] for i in range(9, 0, -1))\n if ans == "":\n return "0" if digits[0] > 0 else ""\n return ans + "0" * digits[0] | 0 | Given an array of digits `digits`, return _the largest multiple of **three** that can be formed by concatenating some of the given digits in **any order**_. If there is no answer return an empty string.
Since the answer may not fit in an integer data type, return the answer as a string. Note that the returning answer must not contain unnecessary leading zeros.
**Example 1:**
**Input:** digits = \[8,1,9\]
**Output:** "981 "
**Example 2:**
**Input:** digits = \[8,6,7,1,0\]
**Output:** "8760 "
**Example 3:**
**Input:** digits = \[1\]
**Output:** " "
**Constraints:**
* `1 <= digits.length <= 104`
* `0 <= digits[i] <= 9` | null |
Python solution faster than 99% with detailed explanation | largest-multiple-of-three | 0 | 1 | A number that is a multiple of three meets the property that the sum of all digits is a multiple of three. \nThus, we can try to find the answer from the three options from the n input digits in the following order: \n1. The answer is composed by all the n digits if the sum of all the n digits is a multiple of three.\n2. The answer is composed by n-1 digits by making the sum of n-1 digits a multiple of three. \n3. The answer is composed by n-2 digits by making the sum of n-2 digits a multiple of three. \n\nFor case 2 and case 3, the digit(s) to remove is the smaller the better. Finally, we can generate the answer by descending order of the available digits. \n\n```\nclass Solution:\n def find_one(self, digits, r):\n for i in range(r, 10, 3):\n if digits[i] > 0:\n digits[i] -= 1\n return True\n return False\n \n def find_two(self, digits, r):\n for i in range(3 - r, 10, 3):\n if digits[i] >= 2:\n digits[i] -= 2\n return True\n elif digits[i] == 1:\n for j in range(i + 3, 10, 3):\n if digits[j] >= 1:\n digits[i] -= 1\n digits[j] -= 1\n return True\n return False\n \n def largestMultipleOfThree(self, digits: List[int]) -> str:\n digits = Counter(digits)\n s = functools.reduce(lambda a, b: (a + b) % 3, [v * c % 3 for v, c in digits.items()])\n \n if s % 3 != 0 and not self.find_one(digits, s % 3) and not self.find_two(digits, s % 3):\n return ""\n ans = "".join(str(i)*digits[i] for i in range(9, 0, -1))\n if ans == "":\n return "0" if digits[0] > 0 else ""\n return ans + "0" * digits[0] | 0 | Given a `m * n` matrix of ones and zeros, return how many **square** submatrices have all ones.
**Example 1:**
**Input:** matrix =
\[
\[0,1,1,1\],
\[1,1,1,1\],
\[0,1,1,1\]
\]
**Output:** 15
**Explanation:**
There are **10** squares of side 1.
There are **4** squares of side 2.
There is **1** square of side 3.
Total number of squares = 10 + 4 + 1 = **15**.
**Example 2:**
**Input:** matrix =
\[
\[1,0,1\],
\[1,1,0\],
\[1,1,0\]
\]
**Output:** 7
**Explanation:**
There are **6** squares of side 1.
There is **1** square of side 2.
Total number of squares = 6 + 1 = **7**.
**Constraints:**
* `1 <= arr.length <= 300`
* `1 <= arr[0].length <= 300`
* `0 <= arr[i][j] <= 1` | A number is a multiple of three if and only if its sum of digits is a multiple of three. Use dynamic programming. To find the maximum number, try to maximize the number of digits of the number. Sort the digits in descending order to find the maximum number. |
Python DP | largest-multiple-of-three | 0 | 1 | ```\nclass Solution:\n def largestMultipleOfThree(self, d: List[int]) -> str:\n dp = [-1,-1,-1]\n for e in sorted(d, reverse=True):\n for a in dp+[0]:\n y = a * 10 + e\n dp[y%3] = max(dp[y%3], y)\n return str(dp[0]) if dp[0] >= 0 else ""\n``` | 0 | Given an array of digits `digits`, return _the largest multiple of **three** that can be formed by concatenating some of the given digits in **any order**_. If there is no answer return an empty string.
Since the answer may not fit in an integer data type, return the answer as a string. Note that the returning answer must not contain unnecessary leading zeros.
**Example 1:**
**Input:** digits = \[8,1,9\]
**Output:** "981 "
**Example 2:**
**Input:** digits = \[8,6,7,1,0\]
**Output:** "8760 "
**Example 3:**
**Input:** digits = \[1\]
**Output:** " "
**Constraints:**
* `1 <= digits.length <= 104`
* `0 <= digits[i] <= 9` | null |
Python DP | largest-multiple-of-three | 0 | 1 | ```\nclass Solution:\n def largestMultipleOfThree(self, d: List[int]) -> str:\n dp = [-1,-1,-1]\n for e in sorted(d, reverse=True):\n for a in dp+[0]:\n y = a * 10 + e\n dp[y%3] = max(dp[y%3], y)\n return str(dp[0]) if dp[0] >= 0 else ""\n``` | 0 | Given a `m * n` matrix of ones and zeros, return how many **square** submatrices have all ones.
**Example 1:**
**Input:** matrix =
\[
\[0,1,1,1\],
\[1,1,1,1\],
\[0,1,1,1\]
\]
**Output:** 15
**Explanation:**
There are **10** squares of side 1.
There are **4** squares of side 2.
There is **1** square of side 3.
Total number of squares = 10 + 4 + 1 = **15**.
**Example 2:**
**Input:** matrix =
\[
\[1,0,1\],
\[1,1,0\],
\[1,1,0\]
\]
**Output:** 7
**Explanation:**
There are **6** squares of side 1.
There is **1** square of side 2.
Total number of squares = 6 + 1 = **7**.
**Constraints:**
* `1 <= arr.length <= 300`
* `1 <= arr[0].length <= 300`
* `0 <= arr[i][j] <= 1` | A number is a multiple of three if and only if its sum of digits is a multiple of three. Use dynamic programming. To find the maximum number, try to maximize the number of digits of the number. Sort the digits in descending order to find the maximum number. |
Sorting Arrays in C++ and Python3✅ | how-many-numbers-are-smaller-than-the-current-number | 0 | 1 | # Code\n```Python3 []\nclass Solution:\n def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:\n test_list = sorted(nums)\n answer = []\n for i in nums:\n answer.append(test_list.index(i))\n return answer\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> smallerNumbersThanCurrent(vector<int>& nums) {\n vector<int>ordered_version = nums;\n vector<int>answer;\n sort(ordered_version.begin(), ordered_version.end());\n \n for (auto it = nums.begin(); it != nums.end(); it++){\n for (int i = 0; i < ordered_version.size(); i++){\n if ( *it == ordered_version.at(i)){\n answer.push_back(i);\n break;\n }\n }\n }\n return answer;\n }\n};\n```\n\n | 2 | Given the array `nums`, for each `nums[i]` find out how many numbers in the array are smaller than it. That is, for each `nums[i]` you have to count the number of valid `j's` such that `j != i` **and** `nums[j] < nums[i]`.
Return the answer in an array.
**Example 1:**
**Input:** nums = \[8,1,2,2,3\]
**Output:** \[4,0,1,1,3\]
**Explanation:**
For nums\[0\]=8 there exist four smaller numbers than it (1, 2, 2 and 3).
For nums\[1\]=1 does not exist any smaller number than it.
For nums\[2\]=2 there exist one smaller number than it (1).
For nums\[3\]=2 there exist one smaller number than it (1).
For nums\[4\]=3 there exist three smaller numbers than it (1, 2 and 2).
**Example 2:**
**Input:** nums = \[6,5,4,8\]
**Output:** \[2,1,0,3\]
**Example 3:**
**Input:** nums = \[7,7,7,7\]
**Output:** \[0,0,0,0\]
**Constraints:**
* `2 <= nums.length <= 500`
* `0 <= nums[i] <= 100` | null |
Sorting Arrays in C++ and Python3✅ | how-many-numbers-are-smaller-than-the-current-number | 0 | 1 | # Code\n```Python3 []\nclass Solution:\n def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:\n test_list = sorted(nums)\n answer = []\n for i in nums:\n answer.append(test_list.index(i))\n return answer\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> smallerNumbersThanCurrent(vector<int>& nums) {\n vector<int>ordered_version = nums;\n vector<int>answer;\n sort(ordered_version.begin(), ordered_version.end());\n \n for (auto it = nums.begin(); it != nums.end(); it++){\n for (int i = 0; i < ordered_version.size(); i++){\n if ( *it == ordered_version.at(i)){\n answer.push_back(i);\n break;\n }\n }\n }\n return answer;\n }\n};\n```\n\n | 2 | You are given an integer array `bloomDay`, an integer `m` and an integer `k`.
You want to make `m` bouquets. To make a bouquet, you need to use `k` **adjacent flowers** from the garden.
The garden consists of `n` flowers, the `ith` flower will bloom in the `bloomDay[i]` and then can be used in **exactly one** bouquet.
Return _the minimum number of days you need to wait to be able to make_ `m` _bouquets from the garden_. If it is impossible to make m bouquets return `-1`.
**Example 1:**
**Input:** bloomDay = \[1,10,3,10,2\], m = 3, k = 1
**Output:** 3
**Explanation:** Let us see what happened in the first three days. x means flower bloomed and \_ means flower did not bloom in the garden.
We need 3 bouquets each should contain 1 flower.
After day 1: \[x, \_, \_, \_, \_\] // we can only make one bouquet.
After day 2: \[x, \_, \_, \_, x\] // we can only make two bouquets.
After day 3: \[x, \_, x, \_, x\] // we can make 3 bouquets. The answer is 3.
**Example 2:**
**Input:** bloomDay = \[1,10,3,10,2\], m = 3, k = 2
**Output:** -1
**Explanation:** We need 3 bouquets each has 2 flowers, that means we need 6 flowers. We only have 5 flowers so it is impossible to get the needed bouquets and we return -1.
**Example 3:**
**Input:** bloomDay = \[7,7,7,7,12,7,7\], m = 2, k = 3
**Output:** 12
**Explanation:** We need 2 bouquets each should have 3 flowers.
Here is the garden after the 7 and 12 days:
After day 7: \[x, x, x, x, \_, x, x\]
We can make one bouquet of the first three flowers that bloomed. We cannot make another bouquet from the last three flowers that bloomed because they are not adjacent.
After day 12: \[x, x, x, x, x, x, x\]
It is obvious that we can make two bouquets in different ways.
**Constraints:**
* `bloomDay.length == n`
* `1 <= n <= 105`
* `1 <= bloomDay[i] <= 109`
* `1 <= m <= 106`
* `1 <= k <= n` | Brute force for each array element. In order to improve the time complexity, we can sort the array and get the answer for each array element. |
Python 3 -> 91.11% faster. 52ms time. Explanation added | how-many-numbers-are-smaller-than-the-current-number | 0 | 1 | **Suggestions to make it better are always welcomed.**\n\n**2 possible solutions:**\n1. For every i element, iterate the list with j as index. If i!=j and nums[j]<nums[i], we can update the count for that number. Time: O(n2). Space: O(1)\n2. This is optimal solution. We can sort the list and store in another temp list. We use dictionary to store the counts and later use it to create result. Time: O(n log n) bcoz of sort. Space: O(n) bcoz of dictionary.\n\n**Explanation of solution 2:**\nnums = 8, 1, 2, 2, 3\n1. We sort the list bcoz we don\'t want to keep traversing the list back and forth. After sorting, we get temp = 1, 2, 2, 3, 8\n2. We traverse temp list. If we find unique element, we know all the previous elements have been recorded. So we add this unique element to the dictionary with index i as value.\nIf duplicate element is encountered, we don\'t add it and don\'t update the value in dictionary.\n3. After the dictionary is constructed, we create output after doing O(1) lookup in dictionary for nums[i]\n\n```\ndef smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:\n\ttemp = sorted(nums)\n\tmapping = {}\n\tresult = []\n\tfor i in range(len(temp)):\n\t\tif temp[i] not in mapping:\n\t\t\tmapping[temp[i]] = i\n\tfor i in range(len(nums)):\n\t\tresult.append(mapping[nums[i]])\n\treturn result\n```\n\n**If this solution helped, please upvote it for others to take advantage of it and learn their techniques** | 201 | Given the array `nums`, for each `nums[i]` find out how many numbers in the array are smaller than it. That is, for each `nums[i]` you have to count the number of valid `j's` such that `j != i` **and** `nums[j] < nums[i]`.
Return the answer in an array.
**Example 1:**
**Input:** nums = \[8,1,2,2,3\]
**Output:** \[4,0,1,1,3\]
**Explanation:**
For nums\[0\]=8 there exist four smaller numbers than it (1, 2, 2 and 3).
For nums\[1\]=1 does not exist any smaller number than it.
For nums\[2\]=2 there exist one smaller number than it (1).
For nums\[3\]=2 there exist one smaller number than it (1).
For nums\[4\]=3 there exist three smaller numbers than it (1, 2 and 2).
**Example 2:**
**Input:** nums = \[6,5,4,8\]
**Output:** \[2,1,0,3\]
**Example 3:**
**Input:** nums = \[7,7,7,7\]
**Output:** \[0,0,0,0\]
**Constraints:**
* `2 <= nums.length <= 500`
* `0 <= nums[i] <= 100` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.